Контактные напряжения в двухвалковом модуле отжима кожи
Автор: К. Ю. Алибоев, Ш.И. Хуррамов
Журнал: Современные инновации, системы и технологии.
Рубрика: Прикладные вопросы и задачи применения систем и технологий
Статья в выпуске: 2 (4), 2022 года.
Бесплатный доступ
В статье приведены результаты моделирования контактных напряжений в двухвалковом модуле отжима кожи. Получены модели распределения контактных напряжений по кривым контакта валков. Найдены выражения угла, определяющие точку максимума нормального напряжения и нейтрального угла в двухвалковом модуле. Выявлено, что точка максимума эпюр нормальных контактных напряжений смещена в сторону начала контакта валков и не совпадает с нейтральной точкой, которая в приводном валке находится на стороне входа слоя материала в зону контакта валков, а в свободном ‒ на стороне выхода.
Двухвалковый модуль, отжим кожи, нормальные напряжения, касательные напряжения, распределения контактных напряжений
Короткий адрес: https://sciup.org/14124588
IDR: 14124588 | УДК: УДК: 677.057 | DOI: 10.47813/2782-2818-2022-2-4-0122-0130
Текст статьи Контактные напряжения в двухвалковом модуле отжима кожи
DOI:
Основным рабочим органом валковых машин для отжима кожевенного полуфабриката является пара рабочих валков с эластичным покрытием (сукном). Пара рабочих валков (валковая пара) и слой кожевенного полуфабриката после дубления (слой кожи) вместе создадут двухвалковый модуль отжима кожи.
В двухвалковом модуле отжима кожи наблюдается одновременное происхождение двух явлений ‒ контактное взаимодействия и фильтрация влаги. В рамках теории валкового отжима кожи данные явления требуют совместного решения двух типа задач, к которым относятся контактные задачи и гидравлические задачи соответственно.
Центральной задачей теории контактного взаимодействия в двухвалковом модуле отжима кожи является моделирование законов распределения нормальных и касательных контактных напряжений.
Решения контактных задач в двухвалковом модуле кожи определяются в первую очередь деформационными свойствами кожи и свойствами покрытия валков, то есть процессом деформирования контактирующих тел двухвалкового модуля [1].
Согласно исследованию [2], деформационные свойства кожи (кожевенного полуфабриката после хромового дубления) при сжатии и восстановлении деформации описываются реологическими моделями Кельвина-Фойгта.
ds j Ej^i + Mj—, (1) dt где Анализ литературы [3, 4] показал, что деформационные свойства материалов, таких как шерсть и техническое сукно, используемые для покрытия валков двухвалковых модулей отжима кожи, также описываются реологическими моделями Кельвина-Фойгта dε j Ejsj + ^j —, где ст., Ej, Ej., н, напряжения, деформация, модули упругости и вязкости покрытия валков при сжатии и восстановлении. МЕТОДЫ Анализ кожевенных валковых отжимных машин [5], показал, что двухвалковые модули отжима кожи в основном имеют симметричный вид. Рассматриваем двухвалковый модуль отжима кожи, в котором валки с радиусами R имеют эластичное покрытие из сукна с толщиной H, толщина кожи равно ^, расстояния между валками равно h , оба валка приводные (рис. 1). Рисунок 1. Схема взаимодействия в двухвалковом модуле отжима кожи Figure 1. Scheme of interaction in a two-roll module for pressing the skin Так как рассматриваемый двухвалковый модуль симметричный, будем исследовать контактное взаимодействие кожи с любым, например, с нижним валком. Кривая контакта нижнего валка (кривая M M ) состоит из двух зон M M и M M . В зоне M M происходит сжатие кожи и покрытия валка, а M M – восстановление деформации. В разработке моделей распределения контактных напряжений основными факторами модели являются напряжения трения валков и формы кривых контакта валков, которые описываются следующими системами уравнений: • модели формы кривых контакта валков [6] /1 = R 1 + к 1 Лv Г 1 + к 1Л1 R r2 =-------- 2 1 + k2 Л Г 1 + к2 Л I cos ^ | cos 0 J cos ^ 2 cos 0 -^< 61< 0, 0 < 02< ^2, 2 H cos a где k 1 = —-— . 2Hcos^ 1 = 51 . Л, Л - показатель, определяющий соотношение скоростей деформирования покрытия валка и кожи при сжатии и восстановлении деформации; • модели напряжений трения [1] < t 1 = tg (61 - А1 +§) n1, 12 = tg02 - А2 + § )n2 , r’ F где а - = arctg —, § = arctg —, F - проекции горизонтальной реакции валка на ось Ox , j rj Q Q - проекции силы давления прижимного устройства и сила тяжести валка на ось Oy . В зоне сжатия нижнего валка выделим элемент длиной dl , направленный по линии n - n, по которой происходит деформация контактирующих тел. На выделенный элемент покрытия валка действуют со стороны слоя материала элементарные нормальная dN и касательная dT силы и реакция отсеченных частей покрытия валка. Составляющие силы dNx и dTx по направлению n - n уравновешиваются силой ст,dlx (рис. 1): Тdli - dN\ cos 0o - dTx sin 00= 0 или Т1 = n1, где стх — напряжение сжатия покрытия валка в направлении n — n , n1 — нормальные напряжения, распределенные по зонам сжатия кривого контакта нижнего валка. В каждой точке зоны сжатия выполняется условие * П1 = т‘ , где Тх* — напряжения сжатия обрабатываемого материала в направлении n — n . Известно [1], что * e1 = A1 1 ^ V cos ф । л 2R sin ф |, A1 cos ^ J (1 + ^ )^ sin ф . Отсюда имеем de* dt — , cos ф] Aa----- tg^1. cos фУх С учетом выражений (7) и (8) из формулы (2) находим с T = A1 E11 V V — cos^! | cos ^ , — cos ф Ц1®----77 tg91 ■ cos Ц J * В этом равенстве т отражает напряжение сжатия кожи в условиях статики. В самом деле, при контактном взаимодействии ст’* отражает напряжение сжатия кожи в реальном динамическом процессе: оно в начале зоны контакта равно нулю, затем увеличивается и достигает значения ттах на линии центров. Исходя из этого, имеем [2] r П1 = B1^(E1 —Ц1®tgФ-^ — cosф ----(E1 + M1®tgB1) , cos Ух J где B1 = Т max . Ex (1 — cos ф) — ^ totg^) Закономерности распределения нормальных напряжений по зоне восстановления деформации кривого контакта нижнего валка определяем аналогично где B2 = r n 2 = B 2 ^ (E 2 + 112.(-ед.Л Т max E2 (1 — cos фт) — ^atg^) . — cos ф Л ---— (E 2 + ^2atg^2) , cos Ф J
Современные инновации, системы и технологии // Modern Innovations, Systems and Technologies
2022; 2(4)
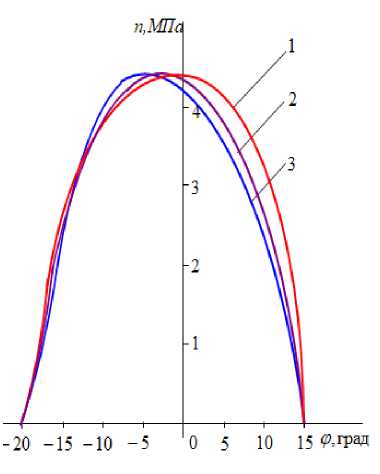
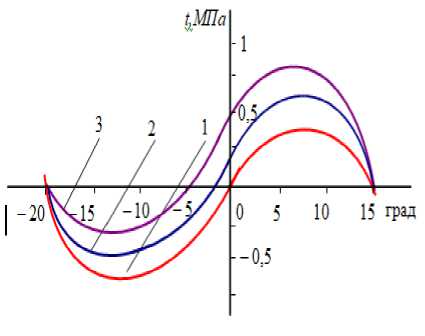
Для определения закономерностей распределения касательных напряжений по контактным линиям валков используем систему (4). Тогда имеем ( cos от. ^ t 1 = B1 (E1 -Mi®tgOTi)--7“(E1 + u.migO.) tg(91 -V1 + £), (11) ^ cos 9 ) РЕЗУЛЬТАТЫ Таким образом, получены математические модели распределения контактных напряжений в двухвалковом модуле отжима кожи с двумя приводными валками: • (9) и (10) - закономерности распределения нормальных напряжений; • (11) и (12) - закономерности распределения касательных напряжений. Анализ полученных математических моделей и их графиков (рисунки 2 и 3) показывает, что закономерности распределения контактных напряжений по контактным линиям валков зависят от коэффициентов трения слоя материала о поверхность контакта Рисунок 2. Графики распределения нормальных напряжений: 1-^- = 0; 2-^-= 0.03; 3-^- = 0.06. Е Е Е Figure 2. Plots of distribution of normal stresses Рисунок 3. Графики распределения касательных напряжений: 1- —= 0; 2-—= 0.05.5; 3-—= 0.1. Q Q Q Figure 3. Graphs of shear stress distribution валков, геометрических, кинематических и деформационных параметров контактирующих тел, а также от сил, действующих на опоры валков. В эпюре распределения контактных напряжений по контактной линии валка особые значения имеют две точки, лежащие на этот кривой. Первая – точка, в которой нормальное напряжение равно максимуму, то есть точка максимума нормального напряжения. Вторая – точка, в которой касательное напряжение равно нулю, то есть нейтральная точка. Установлено [1,6], что точка максимума нормального напряжения находится на стороне входа кожи в зону контакта валка близко к линии центров. Пусть точка максимума нормального напряжения, распределенная по кривой контакта нижнего валка, определяется углом (-ϕ ) . Тогда по условию максимума функции находим µω . ϕ6= 1 E1 В нейтральном угле (-ϕ ) касательная напряжения равняется нулю [6]. Из формулы (12) следует, что tg(-ϕ -ψ (-(ϕ ) +ξ) = 0 . Отсюда имеем ϕ2(1 + k λ cosϕ ) F ⋅ ϕ12 Q ВЫВОДЫ Таким образом, в работе получены модели закономерностей распределения контактных напряжений по кривым контакта валков. На основе анализа графиков контактных напряжений, построенным по полученным моделям (рисунки 2 и 3), выявлено, что: • нормальные контактные напряжения изменяются от нуля в начале и в конце зоны контакта валков до максимума в точке, лежащей влево от линии центров (в сторону начала контакта валков, а точка максимума эпюр нормальных контактных напряжений не совпадает с нейтральной точкой; • касательные контактные напряжения меняют свои знаки в нейтральной точке, которая в приводном валке находится на стороне входа слоя материала в зону контакта валков; величина С = F Q оказывает значительное влияние на эпюру распределения касательных напряжений. Чем больше С , тем левее в приводном валке от линии центров находится нейтральная точка. Увеличение С приводит к увеличению положительных касательных напряжений.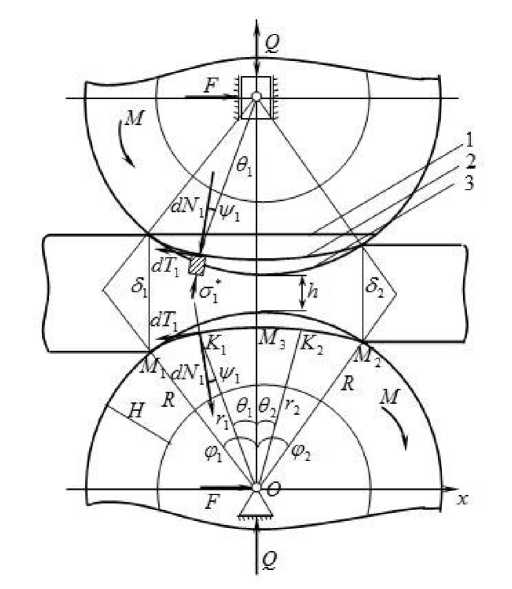
< cos И 7
t2 = В2 (E2 + ^2^tg^2) - cos^2 (E2 + ^2^/g92) tg(92 - ^2 + £). (12)