Контактные силы в аравнениях движения космических аппаратов при стыковке и причаливании

ЯСКЕВИЧ А.В.

Два класса моделей контактного взаимодействия при стыковке и причаливании

Стыковка и причаливание космических аппаратов (КА) представляют собой управляемый механический процесс их сборки на орбите, который выполняется с использованием активного и пассивного стыковочных агрегатов (СтА), их блоков управления, а также системы управления КА или манипулятора. Активный агрегат реализует процесс соединения с помощью механизмов защелок, стыковочного механизма (СтМ) и механизма герметизации стыка (МГС). Каждый такой механизм имеет привод, который выдвигает его в исходное положение перед началом операции и полностью втягивает после ее завершения. Элементы конструкции СтА с направляющими поверхностями обеспечивают уменьшение их рассогласования по мере сближения. На пассивном агрегате они устанавливаются непосредственно на корпусе, на активном — на буферных звеньях СтМ, которые непосредственно контактируют с пассивным СтА. Процесс стыковки начинается с момента первого контакта агрегатов и заканчивается образованием их жесткого соединения. СтА периферийного и центрального типов приведены на рис. 1 и 2.

Рис. 1. Андрогинные периферийные агрегаты: 1 — защелки; 2 — стыковочное кольцо; 3 — пассивный СтА; 4 — направляющие выступы; 5 — стыковочный механизм; 6 — активный СтА

Плоские механизмы защелок могут иметь различные кинематические схемы, но при моделировании стыковки любая защелка с достаточной точностью может быть представлена как звено, имеющее только одну степень подвижности. Она удерживается своей пружиной в некотором исходном, выдвинутом положении, от которого может отклоняться при контакте одной из своих поверхностей с направляющими поверхностями пассивного СтА. Деформированная при контактах пружина после попадания защелки в свободное пространство за соответствующим ответным упором пассивного агрегата возвращает ее в исходное положение. После этого защелка контактирует с этим внешним упором другой поверхностью, сила реакции которой действует на внутренний упор защелки и не приводит к ее относительному движению. Контакты всех защелок с ответными внешними упорами обеспечивают сцепку — первичную механическую связь СтА и стыкуемых КА. Для ее достижения защелки или их механизмы целиком устанавливаются на буферных звеньях СтМ.

Стыковочный механизм устанавливается на корпусе активного СтА. Он компенсирует случайные боковые и угловые рассогласования агрегатов, создавая условия для сцепки, поглощает кинетическую энергию сближения активного КА, выравнивает и стягивает агрегаты, создавая условия для работы МГС. Поэтому он является пространственным и наиболее сложным из всех механизмов СтА, имеет не менее пяти степеней свободы. В СтМ центрального типа буферными звеньями являются головка штыря, ограничители угловых движений, ролики выравнивающих рычагов, а в периферийных — стыковочное кольцо с направляющими выступами конической формы. При моделировании стыковки и особенно причаливания необходимо учитывать механическое сопротивление защелок, а также контактных датчиков, сигнализирующих о наступлении характерных событий — первого контакта, сцепки и т. п. Их контактирующие звенья, как и защелки, имеют одну степень свободы, относительное движение вдоль которой определяется внешним контактным ограничением, а контактная сила реакции — деформацией пружин поджатия.

Механизм герметизации стыка может устанавливаться и на активном, и на пассивном СтА. Его привод заставляет вращаться распределенные равномерно по периферии корпуса плоские кулачковые механизмы активных крюков, которые в процессе своего движения зацепляются за ответные пассивные крюки другого агрегата. Каждый пассивный крюк имеет только одну степень свободы, движению вдоль которой противодействует пружина, нормирующая силу стягивания. После зацепления его положение однозначно определяется положением активного крюка в точке контакта, а контактная сила — силой противодействия нормирующей пружины.

а)

б)

в)

Рис. 2. Агрегаты системы «штырь-конус»: а, б — активный и пассивный СтА; в — головка штыря; 1 — штырь с головкой; 2 — ограничитель угловых движений; 3 — приемный конус; 4 — приемное гнездо; 5 — датчик контакта; 6 — защелка; 7 — датчик сцепки

При стыковке активный КА осуществляет маневры сближения, а пассивный поддерживает заданную ориентацию. При этом, как правило, активный СтА устанавливается на активном аппарате. Однако в некоторых случаях, например, на взлетном лунном модуле, являющемся активным при стыковке, с целью экономии его массы может быть установлен более легкий пассивный агрегат.

Причаливание КА выполняется бортовым манипулятором, который играет роль системы сближения. Поэтому условно считается, что перемещаемый аппарат является активным, а тот, к которому выполняется причаливание, — пассивным. Активный и пассивный СтА могут быть установлены на любом из соединяемых КА. Манипулятор обеспечивает более узкий диапазон начальных условий контакта, поэтому направляющие поверхности обоих агрегатов могут иметь меньшие размеры, а СтМ — более простую конструкцию (в нем, например, могут отсутствовать демпферы) при сохранении нескольких степеней свободы для обеспечения сцепки.

С направляющими поверхностями пассивного СтА могут контактировать различные буферные звенья СтМ, но в каждом отдельном контакте участвуют только два тела. Контакт — это одностороннее ограничение движения двух тел, т. е. в отличие от шарнирного соединения он существует не всегда, а только при выполнении определенных геометрических условий. Физически, т. е. в реальности, такая односторонняя связь реализуется в виде контактной силы, действующей вдоль нормали хотя бы к одной из контактирующих поверхностей. Математические модели контактного взаимодействия при стыковке и причаливании могут быть разделены на два класса.

В моделях первого класса обе контактирующие поверхности принадлежат телам, каждое из которых имеет несколько степеней свободы и может двигаться произвольным образом в зависимости от действующих на него сил. В этом случае контактное взаимодействие рассматривается как динамический механический процесс с односторонними связями. Теория мгновенного удара [1], описывающая перераспределение энергии без учета времени, не используется. Истинное движение контактирующих тел и поверхностей, а также силы реакции определяются в процессе численного интегрирования дифференциальных уравнений динамики, в которых учитывается наличие соответствующих односторонних связей. Модели этого класса описывают взаимодействие СтМ с пассивным СтА. Вследствие дискретности изменения модельного времени условия контакта в них выполняются приближенно, т. е. имеет место внедрение одной контактной поверхности в другую.

В моделях второго класса одна из двух контактирующих поверхностей принадлежит телу, имеющему пренебрежимо малую инерцию и только одну степень свободы относительного движения, которому противодействует пружина. В этом случае можно считать перераспределение энергии незначительным и мгновенным, положение звена с условно нулевой инерцией и направление контактной силы определять положением ответного тела, а величину этой силы — деформацией пружины. Это позволяет обеспечить величину внедрения, близкую к нулю, с любой заданной точностью, которая ограничивается только компьютерным представлением действительных чисел. Модели этого класса описывают взаимодействие защелок и механических датчиков СтМ с пассивным СтА, а также активных крюков одного агрегата с пассивными крюками ответного.

Предметом рассмотрения в данной статье является разработка алгоритмов вычисления контактных сил направляющих поверхностей и их учета в уравнениях движения КА. Специфические физические аспекты контактного взаимодействия [2, 3] не рассматриваются.

Уравнения динамики механических систем при стыковке и причаливании

Движение активного ( s = A ) и пассивного КА ( s = P ) как свободных тел при стыковке описывается уравнениями динамики (УД) Ньютона–Эйлера [4]

m v(I) = αT(f(C,s) + f(C,s)); s s         s R,sC ,s

I(Cs)(.)(Cs) = -ю(Cs) x I(D,s) ю(Cs) + ss      s    ss

+ КC,) x f(C,s) + m (C-s) + m (C,s). CD,s R,s          R ,sC ,s

Здесь и далее верхние индексы в скобках указывают на систему координат (СК), в которой определен вектор или тензор. В частности, ms, Is(C,s) — масса и момент инерции s-го КА в СК XCsYCsZCs, связанной с его центром масс (ЦМ); v. s(I) — ускорение ЦМ s-го КА в инерциальной системе координат (ИСК) XIYIZI; ωs(C,s), ω. s(C,s) — угловые скорость и ускорение КА в СК XCsYCsZCs; αs – матрица направляющих коси-ну,сов, С, К КА относительно ИСК; fC(,Cs,s), mC(,Cs,s) — сила и момент, создаваемые системой управления; fR(,Cs,s), mR(,Cs,s) — сила и момент, действующие на КА со стороны СтМ или пассивного СтА, центры оснований которых определяются векторами l^g5) в СК XC,sYC,sZC,s.

При причаливании движение манипулятора и перемещаемого им условно активного КА ( s = A ) может быть описано с учетом или без учета подвижного основания (пассивного КА — s = P ). Движение такой механической системы описывается УД в замкнутой форме

^A BM ^q BM ^{= b} BM ^,

в которой размерности матрицы A _BM обобщенной инерции, вектора b _BM обобщенных сил и вектора q ^.. _BM обобщенных ускорений соответствуют числу n _BM степеней подвижности манипулятора, перемещаемого КА и подвижного основания. Матрица A _BM и вектор b _BM могут быть рассчитаны наиболее эффективно по алгоритму составного тела [5, 6]. Если расчетная схема манипулятора не приводит к жестким дифференциальным УД, то может быть использована их рекуррентная форма и алгоритм сочлененного тела для расчета ускорений [7–9] .

Звенья СтМ обладают значительно меньшей инерцией, чем КА, поэтому его движение при стыковке и причаливании описывается отдельными УД, учитывающими переносное движение его основания. В наиболее общем виде эти уравнения записываются в замкнутой форме

A _DM q _DM = b _DM ,

Расчет сил контактных реакций для механической системы тел

Несмотря на то, что в реальности контакт двух тел имеет место в некоторой контактной области («пятне»), в математических моделях он представляется точкой, к которой приводятся все силы давления этой области. При дискретном изменении модельного времени и ненулевой инерции двух тел с несколькими степенями свободы относительного движения их точка контакта (ТК) соответствует максимальному взаимному внедрению. Ограничение на движение (наложение связи) в k-й ТК означает равенство в ней проекций скоростей vAC,k и vPC,k активного и пассивного СтА на проходящий через нее единичный вектор nRk нормали к поверхностям контакта nTR,k(vAC,k – vPC,k) = 0.

Из таких условий для K ТК, имеющих место в текущий момент времени, могут быть получены уравнения связей относительно ( n х1)-вектора q обобщенных скоростей всей механической системы (МС) в виде

Hq ^. = 0,                 (4)

где H — (Kхn)-матрица, зависящая от q; q. — вектор обобщенных скоростей, при стыковке q. = [vAT, ωAT, q. TDM, vPT, ωPT]T, при при чаливании q. = [ q. BTM, q. TDM]T.

Если использовать эти уравнения для определения движения МС под действием K контактов, то необходимо объединить уравнение (4) с УД (1) и (3) при стыковке или с УД (2) и (3) — при причаливании. Результатом такого объединения будет система дифференциальноалгебраических уравнений (СДАУ) с индексом 2 [12], который характеризует меру их вырожденности (в одной системе объединяются различные неизвестные — ускорения и скорости). Решение таких систем осуществляется их приведением к одному составу неизвестных с использованием той или иной схемы дискретизации, лежащей в основе неявной схемы численного интегрирования, например, BDF -методов [13]. Для такого подхода характерны наибольшие вычислительные затраты.

Если использовать условие контакта в виде

_T .                .

ⁿ R,k ^{( v} AC,k ^v PC,k ⁾

и сформировать уравнения связей относительно обобщенных ускорений q ^..

H q ^.. + h = 0,                (5)

где h — ( K х1)-вектор, зависящий от q и q , то можно сформировать СДАУ с индексом 1, с общим набором неизвестных — вектором q ^..

A* H T (] ₌ b*

H 0 X - h

где при стыковке A* = diag[AA, AP, ADM], As = diag[ms 13, Is], 13 — единичная (3x3)- матрица; b* = [bA, bPT, bTDM]T, bs, s e {A, P} определяются правыми частями УД (1), а при причаливании A* = diag[ABM, ADM], b* = [bsM, bDM]T; ^ — (Kх1)-вектор множителей Лагранжа.

СДАУ (6) с одинаковым набором неизвестных могут быть проинтегрированы более простыми явными методами, но для этого необходимо применять специальные методы стабилизации решения, например, метод Баумгарта [14], который превращает уравнение (5) перед подстановкой в СДАУ (6) в осциллятор с демпфированием, что обеспечивает затухание ошибок уравнений связей.

При описании ТК кинематическими уравнениями связей УД процессов стыковки и причаливания становятся дифференциально-алгебраическими, и для их решения характерны следующие особенности:

• 1.    Решение СДАУ может быть получено только при условии, что все K уравнений связей (4) или (5) являются линейно независимыми. Это приводит к необходимости реализации процедуры, которая исключает отдельные ТК и, соответственно, искажает реальную контактную ситуацию, затрудняет процесс ее интерпретации.

• 2.    Решение СДАУ позволяет найти только обобщенные реакции Q = H ^T λ временно налагаемых связей, приведенные к степеням подвижности МС. Это не позволяет оценивать реальные контактные силы, которые являются важнейшей характеристикой качества процесса стыковки и используются для оценки нагрузок на конструкцию КА.

• 3.    Решение СДАУ требует больших вычислительных затрат, обусловленных максимальной размерностью уравнений для всей МС, применением либо BDF -методов интегрирования, либо уравнений связей относительно ускорений и методов стабилизации решений.

Совмещение уравнений динамики в рекуррентной форме возможно только с уравнениями связей (5) относительно ускорений. При этом алгоритм вычисления ускорений значительно усложняется

[15], снижается его вычислительная эффективность, УД остаются дифференциальноалгебраическими, требуется применение методов, обеспечивающих устойчивость их численного интегрирования.

Таким образом, уравнения связей, налагаемых в точках контакта, плохо подходят для моделирования процессов стыковки и причаливания. Большую гибкость и вычислительную эффективность обеспечивает непосредственное вычисление контактных сил на основе взаимного внедрения контактирующих тел. В этом случае для каждой k -й ТК, появление которой определяется некоторыми геометрическими условиями, вычисляются следующие параметры:

• •    геометрические параметры контакта — векторы r _AC,k , r _PC,k ее положения в СК контактирующих поверхностей, единичный вектор реакции n Rk и величина A nk взаимного внедрения поверхностей вдоль этого вектора;

• •    кинематические параметры — скорость A n k взаимного внедрения вдоль вектора n _Rk , тангенциальная относительная скорость v _Tk и ее единичный вектор n _Tk ;

• •    динамические параметры — модули контактной силы реакции | f _{R k} | и силы трения | f _{Fr k} |, силы f _{AC k} и f _{PC k} , действующие на контактирующие поверхности активного и пассивного агрегатов, и создаваемые ими моменты m _{AC k} и m _{PC k} .

Алгоритмы определения наличия ТК и их геометрических параметров r _ACk , r PCk , n R k , A n k для различных типов поверхностей будут рассмотрены в следующей работе. Значения кинематических A n k , n _{T k} и динамических f _{AC k} , f _{PC k} , m _{AC k} , m _{PC k} параметров k -й ТК с координатами r _{PC k} = [ x _{PC k} y _{PC k} z _{PC k} ] в СК X _P Y _P Z _P определяются следующими соотношениями:

.

^A n, k = ⁿ R,k ⁽ v AC, k ^— v PC, k ^);

.

v T,k = v AC,k ^- v PC,k ^{- A} n,k n R,k ^;

ⁿ T,k ^{= v} T,k ^{/| v} T,k ^|;

R,k S,k n,k c D,k n,k ^;

| f Fr,k | = k Fr,k | f R,k |;                      (7)

f k ^AC = – n R,k | f R,k | – n T,k | f Fr,k |;

f k ^PC = n R,k | f R,k | – n T,k | f Fr,k |;

m AC,k = r AC,k ^{X f} AC,k ^;

mPC,k = rPC,k X fPC,k’ где kS,k — контактная жесткость (нелинейная функция внедрения ∆n,k); cD,k — коэффициент демпфирования; kFrk — коэффициент трения в точке контакта.

Все параметры контакта вычисляются в СК X _P Y _P Z _P пассивного СтА, в которой ось X _P соответствует направлению сближения активного агрегата. Поэтому единичные векторы контактных реакций, действующих на пассивный СтА, имеют положительные проекции на эту ось и остаются постоянными вследствие неизменности контактирующих поверхностей агрегата в X _P Y _P Z _P . Это позволяет вычислять их до начала моделирования и упростить математические выражения, определяющие другие параметры ТК. Величина ∆ _n,k контактного внедрения в каждой ТК контролируется, если она превышает допустимый предел, то процесс моделирования заканчивается с соответствующим диагностическим сообщением.

Если контакт направляющих поверхностей является демпфированным, т. е. одна из поверхностей является частью буферного звена, которое непосредственно связано с пружинами и демпферами СтМ, то значения коэффициентов k _S,k и c _D,k определяются путем подбора в результате численных экспериментов. Основным критерием при этом является непревышение максимально допустимой величины контактного внедрения A m | x при выбранном шаге численного интегри-рования уравнений движения. Вследствие конечной величины этого шага значения коэффициентов k _S,k и c _D,k отличаются от действующих в реальности. Но влияние погрешности определения этих значений невелико, так как податливость при таком контактном взаимодействии определяется в основном параметрами устройств демпфирования СтМ. Если контакт является недемпфированным, то используется значение k _S,k , полученное экспериментально. Величины коэффициентов трения k _Fr,k уточняются на основе экспериментальных данных – статических измерений и при сравнении данных моделирования процесса стыковки с его воспроизведением на 6-степенном динамическом стенде.

Суммарные сила и момент от всех ТК входят в правую часть УД (3) СтМ и того КА, на котором установлен пассивный СтА (индекс этого КА обозначается далее s(P)). УД всех механических подсистем остаются дифференциальными, независимыми друг от друга и имеют меньшую размерность, чем система уравнений (6). То есть, может быть реализована максимальная вычислительная эффективность алгоритмов моделирования. В отличие от использования уравнений связей легко учитывается контактное трение, и сохраняются все ТК, что упрощает интерпретацию результатов моделирования контактного взаимодействия и расчет нагрузок на любые критические точки конструкции СтА и КА.

Соотношения (7) по своему действию эквивалентны методу Баумгарта, так как выражение для | f _R,k |, с учетом последующего введения этой силы в УД и инерции контактирующих тел, описывает динамику контакта (выполнения связей) в виде осциллятора с демпфированием. При этом требуется минимальный объем вычислений, так как сохраняется исходная структура дифференциальных УД и используются более простые кинематические соотношения для вычисления скоростей v _AC,k , v _PC,k (а не ускорений) поверхностей СтА в ТК.

Относительное положение контактирующих поверхностей и их скорости в ТК определяются через положение и скорости активного и пассивного СтА. При этом, если необходимо учитывать упругие колебания конструкции активного или пассивного КА, то они должны входить в кинематические соотношения движения активного СтА относительно пассивного. Положение центра активного СтА и его ориентация относительно пассивного в СК X _P Y _P Z _P определяется вектором r _DPA и матрицей α _DPA направляющих косинусов

T rDPA αCD,s(P)( rCD,s(P) rPA αPArCD,s(A));

αDPA = αCD,s(A)αPAα CD,s(P), где s(A), s(P) — индексы КА, на которых установлены, соответственно, активный и пассивный СтА (s∈{A, P}); rCD,s = lCD,s + r fD,s; аCD,s = aD,sYCD,s; 1 CD,s, YCD,s — Постоянные вектор положения и матрица ориентации СК СтА в СК ЦМ s-го КА; rDs, afs — вектор и матрица направляющих косинусов, зависящие от упругих деформаций КА в месте установки СтА; rPA, αPA — вектор и матрица преобразования, определяющие положение СК XC AYC AZC A относительно СК XC,PYC,PZC,P.

Абсолютные поступательные и угловые скорости СтА в их локальных СК определяются соотношениями vn = an (v(C,s) + to(C,s) x r(C,s) + vf(Cs));

D,s CD,s s           s         CD,s D,s to D,s = a CD,s (to S C's ) + toDCsO’ в которых vDC), to DC) — скорости линейных и угловых деформаций в месте установки СтА — выражены в СК ЦМ s-го КА. Подробнее метод расчета rDs aDs и vDC), to DC) приведен в работе [4].

^, При стыковке r _PA = α _P ( r _A ^{( I )} – r _P ^{( I )}); α _PA = α _A α _P ^T ; v _s ^{( C s )} = α _s v _s ^{( I )}. При причаливании эти величины определяются расчетной схемой манипулятора и КА, обобщенными скоростями и координатами, полученными при решении УД (2).

Если положение k-й ТК в СК XPYPZP определяется вектором rPCk, то абсолютная скорость пассивного СтА в этой точке равна vPC, k = vD, s (P) + toD, s (P)x 1PC, k •

Система координат x ₀ y ₀ z ₀ основания СтМ совпадает с СК активного СтА. В каждом j -м буферном звене механизма определена СК x _{E j} y _{E j} z _{E j} , относительно которой задается геометрия ее контактирующей поверхности. Положение x _{E, j} y _{E, j} z _{E, j} относительно СК x _j y _j z _j звена определяют постоянные вектор l _{E j} и матрица γ _{E j} направляющих косинусов. П ^, оложение r ⁽ _E ⁰⁾ _, ^, _j и скорость v ⁽⁰ _E ⁾ _{, j} начала СК x _{E, j} y _{E, j} z _{E, j} , матрица τ _{E, j} ее направляющих косинусов относительно x ₀ y ₀ z ₀ вычисляются по рекуррентным кинематическим соотношениям в соответствии со структурой СтМ после решения УД (3). Положение, ориентация и скорости СК x _{E, j} y _{E, j} z _{E, j} относительно СК X _P Y _P Z _P определяются соотношениями

( P )                   T (0)

^r E, j ^r DPA ^α DPA ^r E, j ^;

^α E, j ^{= τ} E, j ^α DPA ^;

v ⁽ P,j = ^a DpA ^{( v} D, s ( A ) ^{+ to} D,s ( A ) ^x rE\ ⁺ v ⁽ j

ω(PE,) j = αTDPA(ωD,s(A) + ωj(0)), где ωj(0) — угловая скорость j-го звена в СК основания СтМ.

Геометрия контактирующей поверхности j -го буферного звена в его локальной СК x _{E, j} y _{E, j} z _{E, j} характеризуется некоторым набором характерных точек, _–задаваемых постоянными векторами c _{E, j, l} , l = 1, L _j и, возможно, связанных с характерными отрезками p _{E, j, l} . Для определения наличия контакта с пассивным агрегатом для этих характерных точек и отрезков вычисляются, соответственно, положение и параметры в СК X _P Y _P Z _P :

(P)        (P)        T r E, j, l r E, j     αE, jcE, j, l ;

(P)         T p E, j, l     αE, jpE, j, l .

Если ТК имеет место, то ей кроме порядкового номера k дополнительно присваивается индекс j буферного звена СтМ.

Вектор r ^{( P} _A ⁾ _{C, k, j} из СК x _{E, j} y _{E, j} z _{E, j} в k -ю ТК и абсолютн ^, а ^, я скорость ^, v ^{( ,P} _A ⁾ _{C, k} ^, _{, j} буферного звена СтМ в этой точке, выраженные в СК

X _P Y _P Z _P , определяются соотношениями

( P )            ( P )         ( P )

^r AC, k, j ^r AC, k ^r E, j ^;

( P )             ( P )         ( P )       ( P )

v AC, k, j      v E, j to E, j x 1 AC, k, j- которые позволяют определить кинематические параметры ТК в соответствии с соотношениями (7). Одно буферное звено может иметь несколько ТК. Суммарные контактные сила fEj = aEj ^ fCh(j) и момент m,. = aT V (r(PV ,, x x f.^> Л, выра-

E,_7 E,j AC , k ( j ) AC,k(j)D¹

женные в СК x _{E, j} y _{E, j} z _{E, j} , преобразуются в СК x _j y _j z _j j -го звена и входят в УД (3), после решения которых определяются сила и момент, действующие в основании СтМ на КА s ( A ). Суммарные сила f _{R, s ( P )} = Σ f _{PC, k} и момент m R,s _{( P} ) = ^ ( r _P C, _k x f _P C, _k ), действующие на пассивный СтА, после преобразования в СК, связанную с ЦМ КА s ( P ), входят в УД (1) или (2).

Приведенные выше кинематические соотношения не зависят от модели движения основания СтМ и пассивного СтА. Они являются вычислительно более эффективными, чем уравнения связей (5) для ускорений даже без учета их вхождения в СДАУ (6).

Расчет сил контактных реакций для защелок и датчиков

Для определения координат точек контакта и контактных сил в моделях второго класса используется метод дихотомии [16], который для задач такого типа реализуется следующим образом. С твердым телом (пассивным СтА), которое может двигаться произвольно, контактирует звено пренебрежимо малой (нулевой) массы, имеющее одну степень подвижности относительно своего основания, буферного звена СтМ. Положение этого звена относительно пассивного агрегата определяется решением УД (1) – (3) и приведенными выше кинематическими соотношениями. При определении точки контакта этого типа оно считается фиксированным. Относительным перемещениям звена нулевой массы внутри его рабочего диапазона противодействует пружина.

Сначала определяется внедрение звена нулевой массы в ответное тело при исходном положении пружины. Если его величина отрицательна, то контакт отсутствует. В противном случае вычисляется внедрение звена в положении, соответствующем максимальной деформации пружины. Если эти две величины имеют различные знаки, то контакт возможен, и осуществляется его итерационный поиск. Для этого определяется величина внедрения в средней точке предшествующего интервала. В новом секторе поиска величины внедрения на его границах должны иметь противоположные знаки. Процесс заканчивается, когда для звена нулевой массы найдены два соседних положения с различными знаками внедрения, находящиеся в пределах заданной точности.

Если внедрение звена нулевой массы положительно и при максимальной деформации пружины, то это означает наличие контакта первого, ранее рассмотренного класса, для его основания — буферного звена СтМ.

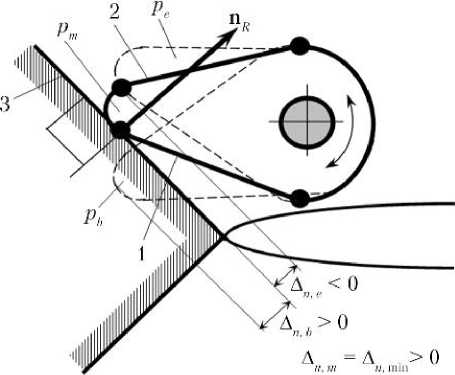
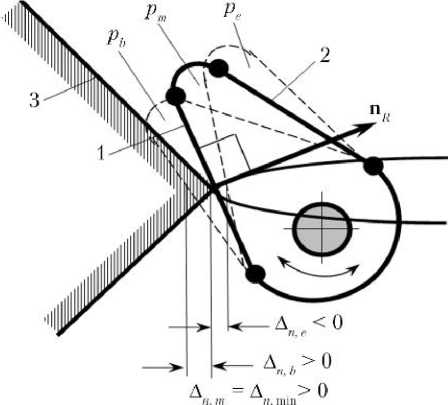
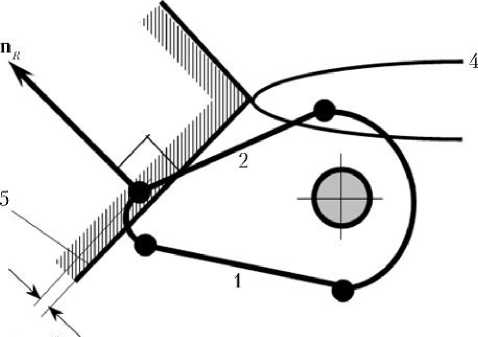
Данный метод коротко иллюстрируется на примере механической защелки поворотного типа, геометрия которой может быть приближенно описана двумя характерными отрезками 1 и 2 , соответствующими ее прямой и обратной поверхностям. Отрезок 1 (прямая поверхность) контактирует с ответными элементами до срабатывания защелки, а отрезок 2 (обратная поверхность) контактирует уже с другим ответным элементом после ее срабатывания. До срабатывания защелки может иметь место контакт конца отрезка 1 (точки) с конической поверхностью или отрезка 1 с окружностью входной грани приемного гнезда (рис. 3, а , б ). В первом случае точка контакта совпадает с концом отрезка 1 , а осевая и боковая составляющие единичного вектора n _R,k реакции являются постоянными в СК X _P Y _P Z _P ; во втором — точка контакта лежит на входной грани, а вектор n _R,k нормален отрезку 1 . Величина контактной силы определяется моментом сопротивления пружины и плечом до точки контакта.

а)

б)

ля>о

в)

Рис. 3. Контакт вращательной защелки до ее срабатывания: а — с приемным конусом; б — с гранью приемного гнезда; в — с механическим упором после срабатывания; 1 — прямая поверхность защелки; 2 — обратная поверхность защелки; 3 — коническая поверхность; 4 — грань – окружность приемного гнезда; 5 — поверхность механического упора (плоскость или конус); p_b, p_e, p_m — положения защелки в начале, конце и середине интервала очередной итерации; ∆ _b, ∆ _e, ∆ _m — величины внедрения в этих положениях; ∆ _n — величина внедрения в механический упор; n _R,k — единичный вектор реакции в точке контакта

На очередной итерации дихотомии интервал поиска заключен между положением p _b с внедрением ∆ _b > 0 и положением p _e с внедрением ∆ _e < 0. Середине этого интервала соответствует положение p _m . После завершения всех итераций контактное положение защелки p _m имеет допустимое внедрение ∆ _n,m > 0.

Аналогично определяются угловые перемещения и контактные силы поворотных датчиков.

Защелка срабатывает, когда конец отрезка 1 находится ниже входной грани приемного гнезда. После этого ее поворот в прямом направлении невозможен из-за отсутствия внешних сил, действующих на прямую поверхность (отрезок 1 ). Поворот в противоположном направлении при контакте ее обратной поверхности (отрезок 2 ) с упором приемного гнезда невозможен из-за наличия у защелки собственного внутреннего механического упора. В этом случае возможен контакт только первого класса (рис. 3, в ) с величиной внедрения ∆ _n > 0, которая зависит от решения УД (1) – (3) механической системы. В этом случае точка контакта совпадает с концом отрезка 2 , а осевая и боковая составляющие единичного вектора n _R,k реакции являются постоянными в СК X _P Y _P Z _P .

Защелки периферийного СтА при моделировании динамики стыковки могут быть представлены звеньями с относительным поступательным движением. Для определения их перемещений в методе дихотомии используется линейный, а не угловой аргумент. Аналогично моделируются датчики поступательного типа.

Валидация моделей контактного взаимодействия

Обоснование корректности геометрических и динамических параметров компьютерной модели и ее соответствия реальному процессу контактного взаимодействия обеспечивается сопоставлением результатов моделирования с данными наземных, а также летных испытаний.

В процессе стыковки до начала жесткого соединения агрегатов основная часть контактов демпфируется стыковочным механизмом, обладающим податливостью большей, чем у элементов конструкции агрегатов и КА. В таких случаях достаточно использовать расчетные значения контактной жесткости. Для отдельных слабо демпфированных контактов проводятся специальные статические и динамические испытания. Окончательная валидация модели производится по данным полунатурных испытаний на 6-степенном динамическом стенде, в котором используются реальные СтА. Один из них устанавливается неподвижно на измерительной платформе с тензометрическими датчиками сил, а второй – на подвижной платформе, позволяющей воспроизводить относительное и угловое движение агрегатов. Управляющий компьютер стенда обеспечивает обработку показаний датчиков сил, интегрирование дифференциальных УД относительного движения активного и пассивного КА и управление подвижной платформой. В результате СтА движутся и контактируют аналогично тому, как это происходит в реальном полете. Каждый отдельный процесс стыковки начинается при начальных условиях, определенных программой испытаний, и завершается после поглощения энергии сближения активного КА, до начала жесткого соединения агрегатов. Данными испытаний являются сохраненные как функции времени измеренные силы и моменты контактного взаимодействия, показания датчиков СтМ, вычисленные параметры относительного движения КА.

Отдельные виды контакта наиболее наглядно проявляются при стыковке с использованием СтА типа «штырь–конус». Пример сравнения данных испытаний на 6-степенном стенде «Конус» РКК «Энергия» и результатов математического моделирования стыковки европейского корабля ATV к Международной космической станции приведен на рис. 4. Показан фрагмент процесса, который начинается с серии ударов головки штыря СтМ в приемный конус, грань и дно приемного гнезда пассивного агрегата. При контакте головки с дном энергия осевого сближения активного КА поглощается сначала пружинным механизмом (меньший уровень силы реакции), а затем фрикционным тормозом (больший уровень) осевого демпфера СтМ. Освобождение накопленной в пружине потенциальной энергии вызывает обратное относительное осевое движение СтА и КА, которому противодействует только небольшая сила трения головки и датчиков в приемном гнезде и которое заканчивается недемпфированным ударом защелок в упоры этого гнезда. В результате имеет место серия ударов со знакопеременной силой реакции с постепенно уменьшающейся амплитудой.

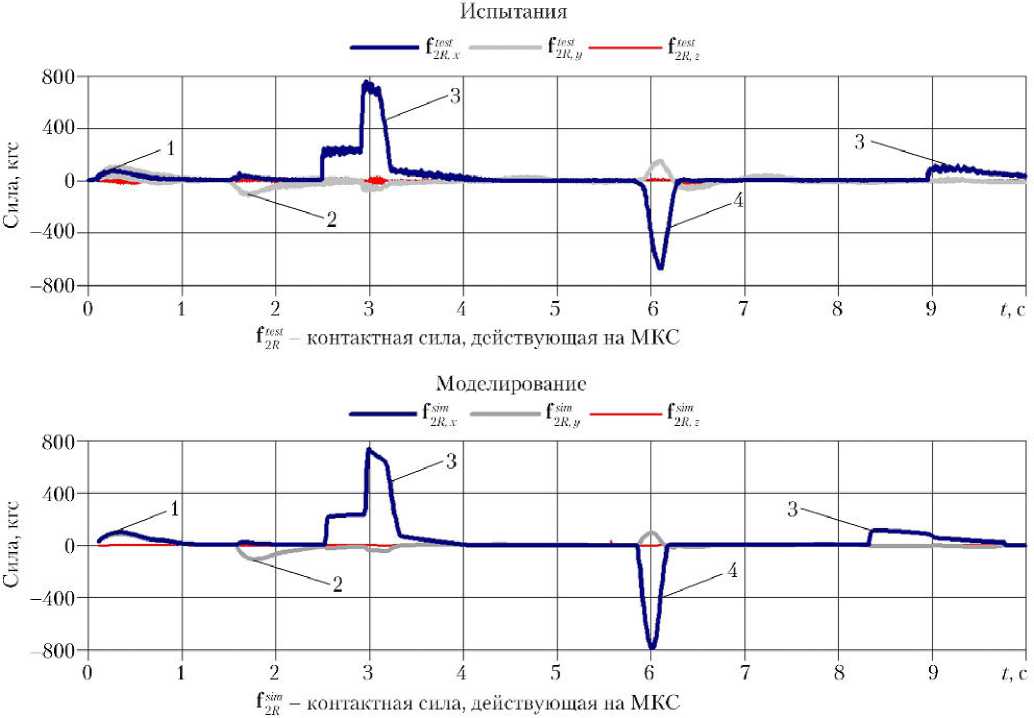
Рис. 4. Контактные силы при стыковке с использованием СтА «штырь–конус»: 1 — контакт головки штыря и поверхности конуса; 2 — контакт головки штыря и защелок с входной гранью приемного гнезда; 3 — контакт головки штыря и дна приемного гнезда; 4 — контакт защелок с упорами приемного гнезда

В процессе реальной стыковки измеряется значительно меньшее число параметров, чем при динамических испытаниях. Система телеметрических измерений передает только показания датчиков СтМ и угловые скорости КА. При послеполетном анализе по специальной технологии определяются приближенные оценки начальных условий движения на момент первого контакта активного и пассивного СтА, которые впоследствии многократно уточняются с использованием математического моделирования. Итерации завершаются при приемлемом совпадении телеметрических данных со значениями, полученными в результате моделирования. В итоге получаются восстановленные динамические параметры реального процесса стыковки.

Заключение

Рассмотренный способ учета контактных ограничений в уравнениях динамики, описывающих процессы стыковки и причаливания космических аппаратов, позволяет детально описать взаимодействие стыковочных агрегатов различного типа и обеспечивает высокую вычислительную эффективность программ моделирования.