Контактные задачи о включении в плоском упругом клине
Автор: Пожарский Д.А., Пожарская Е.Д., Соболь Б.В.
Статья в выпуске: 4, 2024 года.
Бесплатный доступ
Рассматриваются плоские контактные задачи для изотропного однородного упругого клина, на биссектрисе которого расположено тонкое жесткое включение конечной длины. Внешние грани клина находятся в условиях жесткой или скользящей заделки. Задачи симметричны относительно биссектрисы клина. Включение полностью сцеплено с упругой средой в области контакта. К включению приложена касательная сила, под действием которой оно смещается вдоль биссектрисы на заданную величину. При помощи интегрального преобразования Меллина контактные задачи сводятся к интегральным уравнениям относительно касательных контактных напряжений, из которых предельными переходами можно получить интегральные уравнения соответствующих задач для упругой полосы. Частными случаями также являются задачи об одном или двух включениях в упругой плоскости. Вводится основной безразмерный геометрический параметр, характеризующий относительную удаленность включения от вершины клина. Для решения интегральных уравнений применяются три метода. Первый метод состоит в получении замкнутого решения, основанного на специальной аппроксимации символа ядра. Второй метод, регулярный асимптотический, включает разложение решения по степеням малого параметра и эффективен для включений, относительно удаленных от вершины клина. Третий метод, сингулярный асимптотический, связан с разложением решения на несколько частей и решением интегральных уравнений Винера - Хопфа. Берется вырожденное решение и суперпозиция решений типа погранслоя. Этот метод работает для включений, расположенных относительно близко к вершине клина. При помощи трех методов проводится численный анализ для различных типов граничных условий, значений угла клина, коэффициента Пуассона и основного безразмерного параметра.
Теория упругости, плоские контактные задачи, включение, клин, интегральные уравнения, асимптотические методы
Короткий адрес: https://sciup.org/146283045
IDR: 146283045 | УДК: 539.3 | DOI: 10.15593/perm.mech/2024.4.04
Текст научной статьи Контактные задачи о включении в плоском упругом клине
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2024PNRPU MECHANICS BULLETIN
Контактным задачам теории упругости посвящено большое число монографий, изданных как в нашей стране, так и за рубежом [1-10]. Такие задачи возникают в акустике [11] и динамике [12], исследовании поверхностей с периодическим рельефом [13-17], при касании экрана смартфона [18], в пальпационной томографии [19]. При решении контактных задач для ряда тел канонической формы может применяться метод интегральных преобразований [20], а для тел вращения — метод граничных состояний [21; 22]. Краевые и контактные задачи для упругих тел клиновидной формы изучались в [2; 5; 8; 23-25]. Помимо прямых численных методов были развиты асимптотические методы, позволяющие получать решения контактных задач в аналитической форме [2-5; 8]. Получено точное решение контактной задачи о тонком эллиптическом включении в упругом пространстве [26], интегральные уравнения которой получены на основе решения Миндлина [27]. Рассматривались плоские задачи о тонком жестком [26] или упругом [28] включении в полосе. Исследовались периодические системы включений в упругой плоскости [3; 29]. При помощи регулярного асимптотического метода в трехмерной постановке изучались задачи о единичном тонком эллиптическом включении в однородном [30] или составном [31] упругом клине (двугранном угле), а также о периодической системе эллиптических включений в пространственном клине с жестко заделанными гранями [32]. В настоящей статье, по-видимому, впервые рассматриваются плоские контактные задачи о включении в клине. Для решения интегральных уравнений применяются регулярный и сингу- лярный асимптотические методы, а также метод специальной аппроксимации символа ядра интегрального уравнения, приводящий к замкнутому решению. Последний метод позволяет контролировать точность асимптотических решений, но применим не для всех значений угла клина и коэффициента Пуассона.
Интегральные уравнения и метод специальной аппроксимации
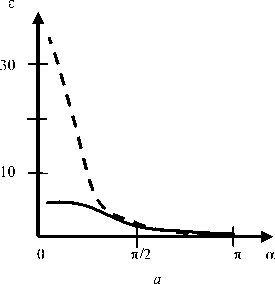
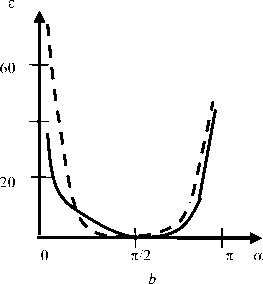
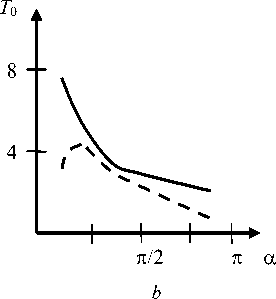
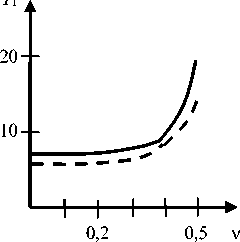
В полярных координатах r, ф рассмотрим упругий клин {rе[0,«); фе[-а,а]} с тонким жестким включением a ф = a : А) ur = 0, иф = 0; B) иф = 0, тгф = 0. Для вывода интегральных уравнений смешанных задач А и B относительно неизвестного касательного напряжения т гф=т( r), a < r< b, ф=0, рассматриваются более простые вспомогательные задачи, в которых граничное условие контакта для Ur при ф=0 заменяется заданием напряжения тмр (на всей полуоси r). Решения этих задач находятся при помощи интегрального преобразования Меллина. Затем, используя условие контакта, получаем интегральное уравнение (0 = G4(1 - v)k-1 , к = 3 - 4v ) b oL f т(р) kI ln— | dp = п05 (a < r < b), I r J a , / , Г L (u) г , k(t)= I —~c°s (ut)du, u А) L (u) = В) L(u) 2k sh2(au) - 2k1u2sin2a к sh(2a u) - u sin(2a) sh(2a u) -к 1u sin(2a) ch(2a u) - c°s(2a) Кроме контактного напряжения требуется определить связь между силой T и смещением 5 при помощи условия равновесия включения b /т( r )dr = T. a Интегральные уравнения (1) можно также вывести из интегральных уравнений соответствующих пространственных задач [30] путем специального предельного перехода к плоским задачам. Поскольку в [30] ядра интегральных уравнений имеют скрытую форму симметрии, предварительно следует их симметризовать путем сдвига контура интегрирования [23, с. 201]. В пределе при a^0, au=t, символ ядра L (u) (1) для задачи B совпадает с известным символом ядра соответствующей задачи о включении в упругой полосе (формула (3.11) в [26]). Рис. 1. Клин с включением Fig. 1. Wedge with an inclusion Важную роль играет асимптотика функций-символов (1) в нуле и бесконечности: L(u) = Au + O(u3) (u ^ 0), L(u) = 1 + O(un exp(-2au)) (u ^ »), A) л = 2Ka2 -2K-‘sin2«, n = 2, (2) 2 Ka - sin(2a) „ , 2a - к 1 sin(2a) B) A =----------—-, 1 - c°s(2a) n = 1, a / n. При a=n, L(u)=cth(nu), задача B соответствует задаче о включении в упругой плоскости. В этом случае интегральное уравнение (1) совпадает с уравнением контактной задачи о вдавливании штампа в упругую полуплоскость и имеет точное решение (формула (6.96) в [5]). Введем безразмерные обозначения x = X In (r / a)-1, p = X ln (p / a )-1, X = 2/ln (b / a), g = X5 / a, (3) ф(р) = рт(р) / (a 0), T. = T / (a 0). Параметр X характеризует относительную удаленность включения от вершины клина. В обозначениях (3) уравнение (1) принимает вид 1 Гр-x /ф(р) k pyidp = ng (I x| < 1). -1 Для получения приближенного решения уравнения (4) при учете свойств (2) используем метод специальной аппроксимации [5] L(u) ® th(Au) (-г < u < г).(5) После взятия интеграла [33] Гth (Au) u cos (ut) du = - In th -nt-4A в ядре уравнения (4) и введения новых переменных [5] приходим к интегральному уравнению Штаермана о вдавливании двух одинаковых штампов в упругую полуплоскость, имеющему точное решение [1]. В результате получим ф( x) =_________________пg exp(n /(2 A/JI_________________ 2 AXK(exp(-n /(AX))X/2[ch(п /(AX)) - ch(пx /(AX))],(6) т1 f мj gK(V1 - exP(-2n /(AX))) T = — ф( x) dx =-----------------------. • X-1 XK (exp(-n /(A X))) Здесь K(t) – полный эллиптический интеграл. Относительная погрешность решения (6) не превосходит относительной погрешности s аппроксимации (5) [5]. Решение (6) является точным в задаче А при a=n, L (u )=th (п u) (включение в плоскости с жесткой заделкой по лучу), а также в задаче B при a=n/2, L(u)=th(пu/2) (два симметричных включения в плоскости). Значение погрешности s чувствительно к коэффициенту Пуассона (рис. 2). Рис. 2. Графики относительной погрешности s(а) (%) для задач А (а) и B (b) при v=0,25 (сплошные линии) и v=0,45 (пунктир) Fig. 2. Plots of relative error s(а) (%) for problems A (a) and B (b) for v=0.25 (solid lines) and v=0.45 (dashed lines) В задаче А при любом угле ае(0,п] погрешность s<6 % при v=0,25 и s<4 % при v=0,5. В задаче B при а^п значение s существенно возрастает при любом V. В связи с тем, что погрешность аппроксимации (5) приемлема не при всех значениях а и V, требуется привлечение других методов. Регулярный асимптотический метод Для относительно удаленных от вершины клина включений (при достаточно больших X) применим метод разложения решения в ряд по степеням малого параметра X-1, который основан на следующей лемме [2; 4; 5]. Лемма. При всех 0≤t<∞ ядро k(t) вида (1) можно представить в форме k (t) = - ln t + F (t), и учесть свойства (2). Из леммы следует, что регулярный асимптотический метод применим при X>a-1. Значения a0, a1 и a2 даны в табл. 1. Таблица 1 Значения постоянных (8) для разных а и V Values of constants (8) for different а and V “ F (t) = Г[L(u)-1]cos(ut) + exp(-u ) du, u причем функция F(t) представима при |t|<2α абсолютно сходящимся рядом F (t) = £ aA2 n, n=0 “ a 0 = rLubl + expC-») ^и, (8) u Разыскивая решение интегрального уравнения (4), (7) в виде ряда по степеням X-1, приравнивая члены при равных степенях этого параметра, получим цепочку интегральных уравнений с логарифмическим ядром, каждое из которых имеет точное решение. В результате получим асимптотическое решение (X^») ф( x ) = a n n г ^-)— [ L (и) -1] и2n-1du (2n)! 0 (n = 1, 2, ...) . Для доказательства леммы следует разложить cos(ut) в ядре (1) в ряд Тейлора, принять во внимание значение интеграла (формула (3.951.8) в [33]) г I exp(-и) - cos( ut) u du = ln t T*X ’ a, , _ a2 (7 - 8 x2 - 8 x4) 1 + -X (1 - 2 x2) + ------4------) + O [-6-1 X 2X (9) п д/1 - x2 , T пд * X Как показывают расчеты, погрешность асимптотического решения (9) при X>2а-1не превышает 5 % (такая же оценка была получена в задаче о вдавливании штампа в грань клина [5]). В табл. 2 дано сравнение асимптотики (9) для интегральной характеристики Table 1 а п/4 п/2 3п/4 п/4 п/2 3п/4 Задача А, V = 0,25 Б, V = 0,25 a0^103 98,2 568 974 193 693 1958 a1^103 368 115 47,6 333 83,3 0 - a 2-103 146 10,1 1,59 109 4,86 -0,369 Задача А, V = 0,5 Б, V = 0,5 a0^103 -620 -193 817 -307 693 2125 a1^103 1017 208 63,4 583 83,3 -9,26 - a 2-103 573 25,7 2,65 213 4,86 0,797 To = XT / g (10) с точным решением (6) для задачи B при а=п/2 и любом V. В выбранном частном случае погрешность асимптотики при X>4n-1не превосходит даже 1 %. Таблица 2 Интегральная характеристика (10) в задаче B при а=п/2 T. = 1 I" Ф( x)dx = g X J X -1 2exp (-2D / X) A AAAD ' f 1 + SE-12 1 Л 2 DD \ —>—1----erf. I--+ L ADD AX 2 AD J \ X S exp (-2E / X) f 12 (D - E) E^A (D -E) V X . (14) При X^ 0 в характеристике (14) можно учитывать главный член асимптотики T. - 2g / (AX2), Table 2 Integral characteristic (10) in problem B for a=n/2 X 0,5 1 2 3 4 Асимптотика (9) 3,82 2,16 1,50 1,26 1,13 Точное решение (6) 3,43 2,15 1,50 1,26 1,13 что соответствует вырожденному решению (11). При D<E в формулах (13) и (14) следует перейти к функции Сингулярный асимптотический метод Для относительно близких к вершине клина включений (при достаточно малых X) используем сингулярный асимптотический метод [4; 5; 23]. При X^ 0 интегрирование в уравнении (4) можно распространить на всю числовую ось и получить вырожденное решение erf AD - E) erfiAE - D) 2 x —, - = —. -, erii(x) = —= exp(t )dt. 4 (D - E) (E - D) ТЛ J ф(x) = g / (AX), (11) Параметры аппроксимации C, D и E и ее относительная погрешность s0 даны в табл. 3 (параметр F находится из второй формулы (12)). Таблица 3 которое справедливо вдали от краев области контакта x = ± 1. Приближенное решение при малых X можно также получить в виде суперпозиции решений типа по-гранслоя, несущих корневые особенности в концах включения x = ± 1 и удовлетворяющих интегральным уравнениям Винера - Хопфа на полубесконечном интервале [34]. Для приближенного решения уравнений Винера - Хопфа применяется идея Койтера [35] аппроксимировать символ ядра на действительной оси легко факторизуемым выражением . им/2+ D2(и2+ E2) DE2 . L (и)~ —5---- ----, = A . (12) V ’ (и2+ С2)(и2+ F2) C2F2 Параметры аппроксимации (12) и погрешность £0 (%) Table 3 Parameters of approximation (12) and error s0 (%) a п/4 п/2 3п/4 п/4 п/2 3п/4 Задача А, v=0,25 B, v=0,25 C 0,960 0,920 0,750 0,990 1,00 0,330 D 0,809 0,878 1,31 3,35 3,30 0,718 E 4,50 1,40 1,70 1,40 2,00 0,800 £0 0,2 0,2 0,2 0,4 0,1 0,6 Задача А, v=0,5 B, v=0,5 C 1,90 0,730 0,890 2,08 1,00 3,30 D 5,27 2,29 1,94 1,65 3,30 0,753 E 1,80 0,700 1,70 3,30 2,00 1,00 £0 1,0 1,0 0,3 0,5 0,1 0,5 В результате асимптотическое решение при малых X получим в виде ф(x)=—( ) 2X Результаты расчетов интегральной характеристики (10) тремя методами приведены в табл. 4. Таблица 4 Интегральная характеристика (10) в задаче А при a=n/4, v=0,5 z( t )=exP(-Dt)+ erf VD + 4 nAt A + S exp (- Et) J A (D — E) erf (D - E) t, Table 4 Integral characteristic (10) in problem A for a=n/4, v=0,5 X 0,5 1 2 3 Решение (6) 10,65 5,77 3,32 2,51 Решение (9) – – 3,40 2,48 Решение (14) 10,19 5,30 – – S = -(C-E)(F-E)/ E , где erf(x) – интеграл вероятности. Интегральную характеристику решения (приложенную к включению силу) на основе (13) найдем в виде На рис. 3 показаны зависимости интегральной характеристики (10) от угла a. Минимальное отличие между жесткой и скользящей заделкой внешних граней клина наблюдается в окрестности угла клина 2a=3n/4. Рис. 3. Графики зависимостей T0(α) при λ=3 (а) и λ=0,5 (b) для задач А (сплошные линии), B (пунктир) при ν=0,25 Fig. 3. Plots of relation T0(α) for λ=3 (a) and λ=0.5 (b) for problems A (solid lines) and B (dashed lines) for ν=0,25 b Рис. 4. Графики зависимостей T1(ν) при λ=3 (а) и λ=0,5 (b) для задач А (сплошные линии), B (пунктир) при α=π/4 Fig. 4. Plots of T1(ν) relation for λ=3 (a) and λ=0.5 (b) for problems A (solid lines) and B (dashed lines) for α=π/4 Отличие между решениями задач А и B нарастает при α→0 и особенно при α→π, когда меняется тип символа ядра интегрального уравнения контактной задачи B с тангенса на котангенс гиперболический (при α=π). На рис. 4 показаны зависимости интегральной характеристики T1=T04(1-ν)/κ=λT /(agG) (15) от коэффициента Пуассона ν (здесь T – размерная сила). Минимальное отличие между жесткой и скользящей заделкой внешних граней клина наблюдается в окрестности значения ν=0,4. Заключение Показана близость решений плоских контактных задач о включении в упругом клине, получаемых по методу специальной аппроксимации символа ядра интеграль- ного уравнения и по асимптотическим методам «больших» и «малых» λ. При уменьшении λ (приближении включения к вершине клина) возрастают контактные напряжения и приложенная к включению сила при смещении включения на заданную величину. При жесткой заделке граней клина (задача А) контактные напряжения и сила больше, чем для случая скользящей заделки (задача B). При определенных углах и коэффициентах Пуассона отличие интегральных характеристик решений контактных задач А и B может быть минимальным. Для несжимаемого материала клина (ν=0,5) интегральные характеристики в обеих задачах существенно возрастают. При уменьшении угла клина интегральная характеристика в задаче А возрастает, а в задаче B достигает максимума при некотором остром угле. При необходимости (в задаче B при α→π) можно усложнить структуру аппроксимации (12) в сингулярном асимптотическом методе по типу аппроксимаций Паде.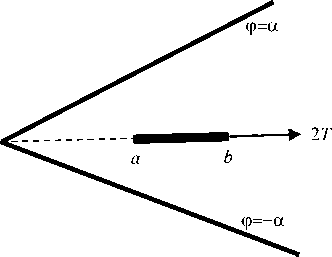
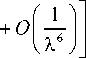
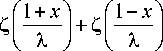
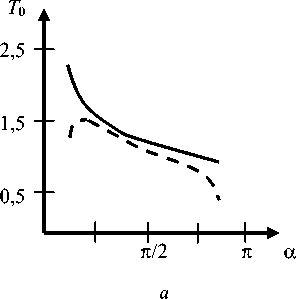
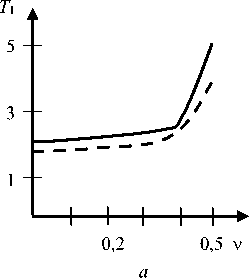
Список литературы Контактные задачи о включении в плоском упругом клине
- Штаерман, И.Я. Контактная задача теории упругости / И.Я. Штаерман. – М., Л.: Гостехиздат, 1949. – 270 с.
- Ворович, И.И. Неклассические смешанные задачи теории упругости / И.И. Ворович, В.М. Александров, В.А. Бабешко. – М.: Наука, 1974. – 456 с.
- Александров, В.М. Контактные задачи для тел с тонкими покрытиями и прослойками / В.М. Александров, С.М. Мхитарян. – М.: Наука, 1983. – 488 с.
- Александров, В.М. Задачи механики сплошных сред со смешанными граничными условиями / В.М. Александров, Е.В. Коваленко. – М.: Наука, 1986. – 336 с.
- Александров, В.М. Контактные задачи в машиностроении / В.М. Александров, Б.Л. Ромалис. – М.: Машиностроение, 1986. – 176 с.
- Gladwell, G.M.L. Contact problems in the classical theory of elasticity / G.M.L. Gladwell. – Alphen aan den Rijn: Sijthoff and Noordhoff, 1980. – 736 p.
- Kalker, J.J. Three-dimensional elastic bodies in rolling contact / J.J. Kalker. – Dordrecht: Kluwer, 1990. – 314 p.
- Alexandrov, V.M. Three-dimensional contact problems / V.M. Alexandrov, D.A. Pozharskii. – Dordrecht: Kluwer, 2001. – 406 p.
- Popov, V.L. Method of dimensionality reduction in contact mechanics and friction / V.L. Popov, M. Heß. – Berlin: Springer, 2015. – 265 p. DOI: 10.1007/978-3-642-53876-6
- Barber, J.R. Contact mechanics / J.R. Barber. – Berlin: Springer, 2018. – 585 p. DOI: 10.1007/978-3-319-70939-0
- Точное решение задачи об акустике в произвольной многослойной среде при контактном взаимодействии с клиновидных штампом / В.А. Бабешко, О.В. Евдокимова, О.М. Бабешко, В.С. Евдокимов // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2023. – № 4. – С. 5–11. DOI: 10.15593/perm.mech/2023.4.01
- Goryacheva, I.G. Dynamics of deformable contacting bodies with sliding, rolling and spinning / I.G. Goryacheva, A.A. Zobova // International Journal of Mechanical Sciences. – 2022. – Vol. 216. – Р. 106981. DOI: 10.1016/j.ijmecsci.2021.106981
- Tsukanov, I.Y. An extended asymptotic analysis for elastic contact of three-dimensional wavy surfaces / I.Y. Tsukanov // Tribology Letters. – 2019. – Vol. 67, no. 4. – P. 107. DOI: 10.1007/s11249-019-1220-5
- Yakovenko, A. The periodic contact problem for spherical indenters and viscoelastic half-space / A. Yakovenko, I. Goryacheva // Tribology International. – 2021. – Vol. 161. – P. 107078. DOI: 10.1016/j.triboint.2021.107078
- Цуканов, И.Ю. К вопросу о контакте волнистого цилиндра и упругой полуплоскости / И.Ю. Цуканов // Прикладная математика и механика. – 2022. – Т. 86, № 5. – С. 685–694. DOI: 10.31857/S0032823522050125
- Lyubicheva, A.N. The influence of 2D periodic surface texture on the partial slip problem for elastic bodies / A.N. Lyubicheva, I.Y. Tsukanov // European Journal of Mechanics / A Solids. – 2022. – Vol. 91. – P. 104405. DOI: 10.1016/j.euromechsol.2021.104405
- Pozharskaya, E.D. Periodic contact problems for a wedge with friction forces taken into account / E.D. Pozharskaya, D.A. Pozharskii, B.V. Sobol // Mechanics of Solids. – 2023. – Vol. 58, no. 5. – P. 1578–1586. DOI: 10.3103/S0025654423700218
- Argatov, I.I. A macro model for electroadhesive contact of a soft finger with a touchscreen / I.I. Argatov, F.M. Borodich // IEEE Transactions on Haptics. – 2020. – Vol. 13, no. 3. – P. 504– 510. DOI: 10.1109/TOH.2020.2969628
- Argatov, I.I. Collective indentation as a novel strategy for mechanical palpation tomography / I.I. Argatov, X.Q. Jin, L.M. Keer // Journal of the Mechanics and Physics of Solids. – 2020. – Vol. 143. – P. 104063. DOI: 10.1016/j.jmps.2020.104063
- Уфлянд, Я.С. Интегральные преобразования в задачах теории упругости / Я.С. Уфлянд. – М.-Л.: изд-во АН СССР, 1963. – 368 с.
- Иванычев, Д.А. Решение контактной задачи теории упругости для анизотропных тел врщения с массовыми силами / Д.А. Иванычев // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2019. – № 2. – С. 49–62. DOI: 10.15593/perm.mech/2019.2.05
- Иванычев, Д.А. Два способа организации скалярного произведения в методе граничных состояний / Д.А. Иванычев // Вестник Донского государственного технического университета. – 2020. – Т. 20, № 1. – С. 15–24. DOI: 10.23947/1992-5980-2020-20-1-15-24
- Пожарский, Д.А. Фундаментальные решения статики упругого клина и их приложения / Д.А. Пожарский. – Ростов н/Д: ООО «ДГТУ-Принт», 2019. – 312 с.
- Keer, L.M. Hetenyi's elastic quarter space problem revisited / L.M. Keer, J.C. Lee, T. Mura // International Journal of Solids and Structures. – 1983. – Vol. 19, no. 6. – P. 497–506.
- Keer, L.M. A contact problem for the elastic quarter space Hetenyi's elastic quarter space problem revisited / L.M. Keer, J.C. Lee, T. Mura // International Journal of Solids and Structures. – 1984. – Vol. 20, no. 5 – P. 513–524.
- Александров, В.М. Тонкие концентраторы напряжений в упругих телах / В.М. Александров, Б.И. Сметанин, Б.В. Соболь. – М.: Наука, 1993. – 224 с.
- Mindlin, R.D. Force at a point in the interior of a semiinfinite solid / R.D. Mindlin // Physics. – 1936. – Vol. 7, no. 5. – P. 195–202.
- Грилицкий, Д.В. Распределение напряжений в полосе с упругим тонким включением / Д.В. Грилицкий, А.А. Евтушенко, Г.Т. Сулим // Прикладная математика и механика. – 1979. – Т. 43, вып. 3. – С. 542–549.
- Грилицкий, Д.В. Периодическая задача для упругой плоскости с тонкостенными включениями / Д.В. Грилицкий, Г.Т. Сулим // Прикладная математика и механика. – 1975. – Т. 39, вып. 3. – С. 520–529.
- Александров, В.М. Задача о включении в трехмерном упругом клине / В.М. Александров, Д.А. Пожарский // Прикладная математика и механика. – 2002. – Т. 66, вып. 4. – С. 635–646.
- Александров, В.М. Пространственная задача о тонком включении в составном упругом клине / В.М. Александров, Д.А. Пожарский // Прикладная математика и механика. – 2011. – Т. 75, вып. 5. – С. 843–849.
- Pozharskaya, E.D. Periodic system of rigid inclusions in a spatial elastic wedge / E.D. Pozharskaya // Тенденции развития науки и образования. – 2023. – № 96, ч. 9. – С. 177–180. DOI: 10.18411/trnio-04-2023-501
- Градштейн, И.С. Таблицы интегралов, сумм, рядов и произведений / И.С. Градштейн, И.М. Рыжик. – М.: Наука, 1971. – 1108 с.
- Нобл, Б. Метод Винера Хопфа / Б. Нобл. – М., Л.: Изд-во иностр. лит., 1962. – 276 с.
- Koiter, W.T. Approximate solution of Wiener Hopf type integral equations with applications. Part I-III / W.T. Koiter // Koninkl. Ned. Akad. Wetenschap. Proc. Ser.~B. – 1954. – Vol. 57. – P. 558–579.


