Контракции калибровочных групп и спонтанное нарушение симметрии

Калибровочные теории были предложены Янгом и Миллсом в 1954 г. [1] и в настоящее время рассматриваются как наиболее успешный метод описания фундаментальных взаимодействий в физике частиц, где в основном используются компактные полупростые группы. Например, единое описание электромагнитных и слабых взаимодействий в рамках стандартной модели Вайнберга–Салама [2,3] основано на калибровочной группе SU (2) х U (1) .

Наппи и Виттеном было замечено [4], что можно рассматривать калибровочные теории и для неполупростых групп, обладающих невырожденной инвариантной билинейной формой. Такие теории имеют более простую структуру по сравнению со стандартными моделями с полупро-стыми калибровочными группами. Позже появились работы [5, 6], в которых рассматривались калибровочные тео- рии, отвечающие различным неполупростым группам. Контракции стандартной электрослабой модели Вайнберга– Салама к калибровочной группе SU(2; е) х U(1) описаны в [7].

В данной работе рассматривается механизм спонтанного нарушения симметрии (механизм Хиггса) для калибровочных моделей, основанных на неполупростых группах. Такие группы в фундаментальном представлении являются группами преобразований расслоенных пространств с вырожденной метрикой и могут быть получены из классических простых групп контракциями (предельными переходами). Последовательность обнуления слагаемых лагранжиана в процессе предельного перехода задается явной зависимостью лагранжиана от параметра контракции.

1.    Калибровочная теория для группы SO(2; е). 1.1.    Единое описание модели. Рассмотрим преобразование SO(2) калибровочной модели в галилееву калибровочную теорию с помощью контракции группы вращений в группу Галилея. Пространство Ф2(е) и группа G2 = SO(2; е) Галилея могут быть получены из евклидовой плоскости Ф2 и группы SO(2) введением параметра контракции е и заменами ф2 ^ еф2, а ^ еа, при е ^ 0. Калибровочные преобразования

( ^ф 1 ⁽ x )

\ ^еф 2 ⁽ x )

I    cos еа (x )

I — sin еа (x )

sin еа ( x ) cos еа ( x )

A ( ^ф 1 ^{( x} ) A

J \ ^еф 2 ⁽ x ) )

оставляют инвариантной форму ф ^t ( е ) ф ( е ) = ф 1 + е ² ф 2 , которая при е =1 определяет евклидову метрику в пространстве Ф ₂ .

Чтобы проследить поведение слагаемых при переходе к пределу, введем параметр ϵ в стандартный лагранжиан [8]

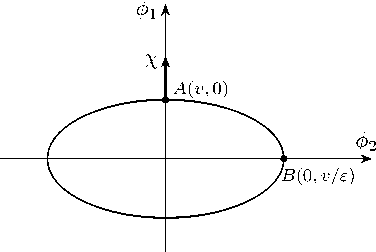
Рисунок 1. Эллипс вакуумов лагранжиана L ( е ) .

Figure 1. Ellipse of vacua of the Lagrangian L ( е ) .

Рассмотрим малые возбуждения х ( x ) компоненты поля ф 1 ( x ) относительно выбранного вакуума ф 1 ( x ) = v + X ( x ) (рис. 1). За счет калибровочных преобразований (1) компонента ф ₂ ( x ) становится отличной от нуля. Подстановка поля материи ф = ^ v +ф 2 ^х ^ приводит лагранжиан к виду

^{L ( е} ) = L b ^{+ е 2 L} s ^,

L b = |( ^д , х ^{) 2 —} V ² X ^{2 —} ^'-Фх ^{3 —} | X 4 •

L ^{( е} ) = ^{— е} 2 4 F ,v F ,v + ^ [⁽ D , ^ф 1 ^{) 2} + ^{е 2 (} D , ^ф 2 ^{) 2} ] ^—

1          e ² v ²

L s = ^— 4 B ,v ⁺  2 B , ⁺ e^A , ^{( ф} 2 ^д , ^{х — хд} , ^ф 2 ) ⁺

— 4 [(ф 1 + е2ф2)2 - v2]2 .(2)

где ковариантные производные даны соотношением

D , ф ( е ) = д , ф ( е ) + ее^Тф ( е ) ,

( D, ф1          д,    ееА, X ,1

ϵD µ ϕ ^′ ₂         -ϵeA µ ∂ µ ϵϕ 2

т. е.

D , ^ф 1 = ^д , ^ф 1 + ^е 2 e^A , ^ф 2 ,

D,ф 2 = д,ф 2 — еА,ф 1 ■

Механизм спонтанного нарушения симметрии (механизм Хиггса [9]) – это способ наделить массой калибровочные поля. Лагранжиан (2) имеет набор основных состояний, которые достигаются при нулевых векторных полях A , = 0 и ковариантно постоянных полях материи D , ф = 0 , обеспечивающих минимум потенциала V ^{( ф ( е} )) = [ ^ф 1 + ^{е 2 ф} 2 ^— v ^{2 ]} 2 , т. е.

^ф 1 + ^{е 2 ф} 2 = v ² ,

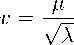
Все основные состояния (рис. 1) (при е = 0) можно получить с помощью калибровочных преобразований из одного из них, например, ф vac=( v )• v=S (6)

отвечающего точке A ( v, 0) на рис. 1.

+ vx ( e ² A 2. — Аф 2 ) + 2 X 2 ( e 2 A , — Аф 2 ) • (7)

где B , = A , — eV д , ф ₂ - калибровочное векторное поле с массой m B = ev = ^ =, х — скалярное поле (хиггсов-ский бозон) с массой m _x = ц ² , а также включены слагаемые, описывающие взаимодействия полей. При малых ϵ поле ϕ 2 за счет калибровочных преобразований связано с вакуумом соотношением ф ₂ ( x ) = а ( x )( v + х ( x )) . Вводя векторное поле B , = A , — eV д , а , преобразуем лагранжиан L s к виду, содержащему только поле B , и его взаимодействия с полем χ

1 ₂      e ² v ² _{2       2    2} e ² _{2 2}

L s = ^— 4 B ,v ⁺  2 B , ^{+ ve X}B , ⁺ у ^х B , ⁽⁸⁾

Теория с калибровочной группой SO(2; е) может быть получена из теории с группой SO(2) подстановкой v → v, ϕ1 → ϕ1, ϕ2 → ϵϕ2,

A _µ → ϵA _µ , F _µν → ϵF _µν . (9)

• 1.2.    Калибровочная модель для группы Галилея G ₂ . Теория с калибровочной группой Галилея G ₂ получается из теории с группой SO (2) переходом к пределу е ч 0 . В этом пределе пространство полей материи Ф ₂ превращается в двумерное тривиально расслоенное пространство Ф ₂ ( е ) , в котором ось {ф 1 } есть одномерная база, а ось {ϕ 2 } представляет одномерный слой. Инвариант ф ^t ( е ) ф ( е ) = ф 1 + е ² ф 2 распадается на два инварианта : inv 1 = ф 1 относительно общих преобразований (1) ф 1 = ф 1 , ф' ₂ = ф ₂ — аф 1 и inv ₂ = ф 2 относительно только дискретных преобразований ф 2 = ±ф ₂ в слое

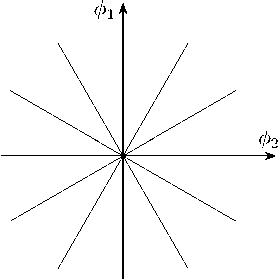
Рисунок 2. Пучок прямых на плоскости Евклида E 2 .

Figure 2. Bundle of lines on the Euclidean plane E 2 .

( ф 1 = 0) . Поэтому в пространстве Галилея есть две метрики : одна в базе, а другая в слое. Учтем в дальнейшем эту особенность.

Пучок прямых, проведенных через точку, на этих двух плоскостях имеет разные свойства относительно автоморфизмов плоскости [10]. На евклидовой плоскости любые две прямые пучка совмещаются друг с другом вращениями вокруг точки (рис. 2). На плоскости Галилея (рис. 3) в пучке есть одна изолированная прямая, которая не совмещается с любой другой прямой пучка вращениями вокруг точки, т. е. преобразованиями Галилея.

ϕ 1

χ

A ( v, 0)

ϕ 2

Рисунок 3. Пучок прямых на плоскости Галилея G 2 .

• Figure 3.    Bundle of lines on the Galilean plane G 2 .

Если интерпретировать эти плоскости в некотором физическом контексте, тогда на евклидовой плоскости все прямые должны иметь одну и ту же физическую размерность [ ф 1 ] = [ ф 2 ] . На плоскости Галилея имеется бесконечно много прямых с той же физической размерностью, что и размерность базы [ ф 1 ] и одна изолированная прямая, имеющая некоторую другую размерность [ ф 2 ] = [ ф 1 ] [11]. Например, при интерпретации пространства Галилея как пространства-времени классической физики база рассматривается как ось времени и имеет размерность [сек], а слой моделирует собственно пространство и имеет размерность [см].

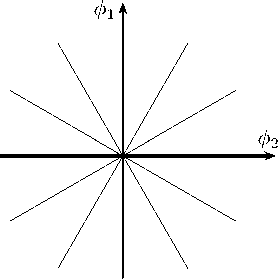
Представления (7), (8) указывают порядок стремления к нулю слагаемых в лагранжиане при переходе к пределу е ^ 0 . Вначале считаем малым лагранжиан L s , пропорциональный ϵ ² , затем в остатке получаем поле χ в базе (рис. 4) с лагражианом L b = L _x . Можно рассматривать и обратный процесс восстановления полей и взаимодействий при изменении параметра контракции ϵ от нуля до единицы.

Рисунок 4. Основные состояния модели с калибровочной группой Галилея G 2 .

• Figure 4.    Ground states of the model with the Galileo gauge group G 2 .

Другой выбор основного состояния отвечает точке B (0 , v ) на рис. 1. В пределе е ^ 0 она попадает в слой ф 1 = 0 ,ф 2 и описывается вектором o va. = (0 , е v ) t = (0 , v ) t . Лагранжиан (2) в слое инвариантен только относительно дискретной калибровочной симметрии ϕ 2 → -ϕ 2 . Малые возбуждения ξ поля ϕ 2 в окрестности этого вакуума описываются полем материи вида (рис. 5)

ф ( x ) = Г     °tn V v = ^=.    (10)

^v + ^е€ ⁽ x )            /л

Подставив его в общий лагранжиан (2), получим лагранжиан в слое

L ^{( е} ) = ^{е 2 L} f =

= е ² [|(■ . - Л 2 € 2 — Л~Ы 3 — ‘ 2 4( 4 ] ■   (11)

Л V ( ф 2 )

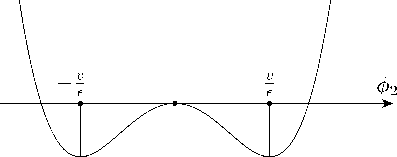
ξ     ϕ 2

- v 0 v ϵϵ

Рисунок 5. Потенциал V ( ф 2 ) и основные состояния лагранжиана в слое ( ^ф 1 = 0 ^,ф 2 ) .

Figure 5. Potential V ( ф 2 ) and ground states of the Lagrangian in fiber ( ^ф 1 = ^{0 ,ф} 2 ) .

Лагранжианы в базе Lχ (7) и слое Lf (11) имеют одинаковый вид, совпадающий с формулой (5.8) в монографии [8] для лагранжиана возмущений скалярного поля φ с дискретной симметрией φ → -φ. Лагранжиан Lχ (7) не инвариантен относительно замены χ → -χ, так же как Lf (11) не инвариантен относительно замены ξ → -ξ, поскольку основные состояния не инвариантны. След симметрии φ → -φ в лагранжианах Lχ, Lf остался в виде соотношения между массой поля µ2 и константами кубичного и четверного взаимодействий. Таким образом, в калибровочной теории с группой Галилея G2 поле материи (хиггсовский бозон) χ в базе и калибровочное поле Bµ в слое представляют физически разные поля с разными физическими размерностями, подобно тому, как время (база) и пространство (слой) в пространстве-времени Галилея являются разными физическими сущностями. Тем не менее размерности масс хиггсовского бозона тх = ^2ц и векторного бозона mB = ev = ^ одинаковы и в точности таковы же, как и в неконтрактированной SO(2) калибровочной теории.

В калибровочной теории с группой SO (2; е ) при е = 0 в качестве вакуума можно выбрать любое основное состояние на эллипсе рис. 1. Однако для того, чтобы получить теорию с полной, зависящей от одного вещественного параметра группой Галилея G ₂ при переходе к пределу е ^ 0 , необходимо, чтобы выбранный вакуум принадлежал базе в этом пределе (см. рис. 4). Если же вакуум модели отвечает, например, точке B на рис. 1, то в пределе получаем модель с дискретной симметрией, являющейся дискретной подгруппой исходной калибровочной группы.

2.    Калибровочные теории с группами SO(3; е) 2.1.    Единая калибровочная модель. Ортогональная группа Кэли-Клейна SO(3; е), е = (е 1 ,е2) определяется [11] как группа преобразований вещественного пространства Ф3(е), оставляющая инвариантной квадратичную форму фt (е) Ф(е ) = ФI +е 1Ф 2 +е 1е 2 Ф 3 ■         (12)

Калибровочные преобразования полей материи Ф ( е ) осуществляются элементами ш ( x ; е ) G SO (3; е ) в виде

Ф ‘ ( x ) = ш ( x ; е ) Ф ( x ) ,

/ Ф 1 \

I      ^е 1 ^Ф 2 I =

ϵ 1 ϵ 2 ϕ ^′ ₃

ω 11   ϵ 1 ω 12   ϵ 1 ϵ 2 ω 13             ϕ 1

• ^ϵ 1 ^ω 21      ^ω 22      ^ϵ 2 ^ω 23            ^ϵ 1 ϕ 2     . (13)

• ^ϵ 1 ^ϵ 2 ^ω 31   ^ϵ 2 ^ω 32        ^ω 33         ^ϵ 1 ^ϵ 2 ϕ 3

Здесь контракционные параметры независимо стремятся к нулю е _к ^ 0 , к = 1 , 2 ■ Генераторы алгебры Ли so (3; е ) имеют вид

	0	-ϵ 1	0		0	0	-ϵ 1 ϵ 2
T 1 =	ϵ 1	0	0	, T 2 =	0	0	0
	0	0	0		ϵ 1 ϵ 2	0	0

00  0

T 3 =    0   0 -е 2                 (14)

0 е 2      0

и удовлетворяют коммутационным соотношениям

[ T 1 ,Т 2 ] = е 1 T 3 , [ T 2 ,Т 3 ] = е 2 T 1 , [ T 3 ,Т 1 ] = T 2 . (15)

Калибровочные поля принимают значения в алгебре so (3; е )

A , ( x ) = gT A ( x ) =

• /    ^{0      - е} 1 A , ^{- е} 1 ^е 2 A , \

• = g     е 1A,      0      -е 2 A,     ■

\ е 1е 2 A,   е 2 A,       0/

Тензор напряженности

F,v(x) = dA (x) - dvA, (x) + [A,(x) ,Av(x)] = = gT a FO, (x)

в компонентах имеет вид

F^ = d , A V - д , A , + е 2 g ( A A , — A , A V ) ,

F ,v = d , A ²v - д , AI + g ( A , A V — A A V V ) ,

3   3   321221

F,v = д,Av - dvA, + е 1g(A,AV - A,Av) ■

Ковариантная производная задается соотношением

D , Ф ( е ) = [ д , + gT ( A , )] Ф ( е ) или в матричном виде

(    D , Ф 1 \

I     ^е 1 ^D , ^ф 2 I =

ϵ 1 ϵ 2 D µ ϕ 3

/       ^д ,   ^{- е} 1 ^gA ,   ^{- е} 1 ^е 2 ^gA , \ /      ^Ф 1 \

= I     ^е 1 ^gA ,         ^д ,     ^{- е} 2 ^gA ,  I I     ^е 1 ^Ф 2   I

ϵ 1 ϵ 2 gA ² _µ     ϵ 2 gA ³ _µ           ∂ µ        ϵ 1 ϵ 2 ϕ 3

и действует на компоненты поля Ф ( е ) по формулам

^D , ^ф 1 = ^д , ^Ф 1 ^{- gе} 1 ⁽ A , ^Ф 2 + ^е 2 A , ^Ф з ) ,

D,ф2 = д,Ф2 + g(A,Ф 1 - е2A 1ф3) , D,ф 3 = д,Ф 3 + g ( A ,Ф 1 + A ,Ф 2 ) ■

Полный лагранжиан модели L ( е ) = L A ( е ) + L ф ( е ) определяется как сумма лагранжиана калибровочных по-

L A ^{( е} )=8 g 2 Tr< f ,v ^{( е )) 2} =

= - 4[ е 2( F1 )2 + е 1 е 2 (Fj, )2 + е 2( F*, )2]

и лагранжиана полей материи

Lф(е) = 2(D^(е))t(D ,Ф(е)) - V(Ф; е),(22)

где потенциал выбирается в виде

• V (Ф; е ) = | ^t (е) Ф (е) -     ^ ,(23)

В явном виде с учетом (18) калибровочный лагранжиан запишется т (,Д        [..2/ т-1 ^2 । ,2 2/ -£-2 \2 । 2/ -£-3 \2]

L A ^{( е} ) = ^- [^е 1 ^{( F} ,v ) + ^е 1 ^е 2 ^{( F} , v ) + ^е 2 ^{( F} ,v ) J -

• ^{- е} 1 ^е 2 [ L А ^{3)( е} ) + L а ^{)( е} )] ■            ⁽²⁴⁾

Слагаемые третьего и четвертого порядков по полям равны

L А ³⁾( е ) = 2 g [ F 1 v ( A , A V - A , A V ) +

+ F v ⁽ A , A V ^- A , A V ) + F v ⁽ A , A V ^- A ², A V )] , L A (е ) = g ² [ е 2 ( A , A V - A , A V ) ² +

+ ( A , A V - A , A V ) 2 + е 1 ( A , A V - A , A V ) ² ] , (25)

a F a_v = d ^ A V -d _v A a есть тензор напряженности в плоском пространстве.

Основные состояния лагранжиана L ( е ) = L A ( е ) + L ф ( е ) представляют собой конфигурацию полей, обнуляющих калибровочный лагранжиан L A ( е ) = 0 и доставляющих минимум потенциалу (23). Основные состояния реализуются на полях

Aм(x; е) = w(x; е)дмw 1(x; е), w(x; е) 6 SO(3; е), ф‘(е) Ф(е) = Ф1 + е 1Ф 2 + е 1е 2 Ф 3 = v 2, v=

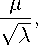
которые при A _M ( x ; е ) = 0 лежат на эллипсоиде («сфере» радиуса v ) (рис. 6) в пространстве полей материи, задаваемом уравнением (26), и могут быть получены калибровочными преобразованиями

ф(x ; е ) = w (x ; е ) $ v^ac ,

A' ^ ( x ; е ) = w ( x ; е ) A _м ( x ; е ) w - ¹ ( x ; е ) +

+w(x; е)d^w-1 (x; е)

из одного основного состояния, выбираемого из соображений простоты в виде

A ^ ( x ; е ) = 0 , ( ф ^vac ) t = ( v, 0 , 0) t (28)

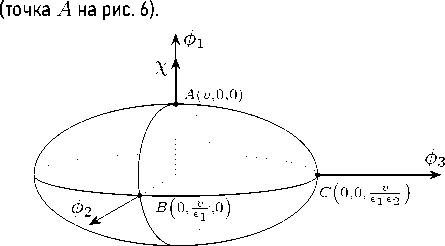
Рисунок 6. Эллипсоид основных состояний лагранжиана L ( е ) .

Figure 6. The ellipsoid of the ground states of the Lagrangian L ( е ) .

Далее в механизме Хиггса рассматриваются малые (линейные) возбуждения поля ϕ1 в окрестности вакуума ф 1(x) = v + X(x), ф2(x), фз(x).(29)

Для нового поля ф ( x ) полный лагранжиан модели принимает вид

L (е) = L (2)( е) + L (3)( е) + L (4)( е).(30)

Квадратичный по полям лагранжиан

L ⁽²⁾ ( е ) = 2( д _ц х ) 2 - Ц ² X 2 +

+ е 2 [ - 4( B 1 v ) 2 + g^ ( B 1 ) 2 ] + е 2 [ - 4( F 3, ) ² ] +

+е2е2 [-4(B2,)2 + g^(B2)2] .(31)

где введены новые поля

B1 = A J +    дМф2,  B2 = Aм +    дМф3 , описывает массивное скалярное поле материи х, тх = 2^ц — хиггсовский бозон, два массивных векторных поля (к = 1,2) с одинаковыми массами Bkk, mB = gv = ^ и безмассовое поле A3µ. Взаимодействия полей описываются слагаемыми третьего L(3)(е) и четвертого L(4)(е) порядков по полям

L (3^{) ( е} ) = ^—^^х 3 ^{+ е} 1 { ^- ^^vX ^{( ф} 2 ^{+ е} 2 ^ф 3 ⁾⁺

⁺ g [ A М ^{( хд} м ^ф 2 ^{- ф} 2 ^д М ^х ) ⁺

^{+ е} 2 A М ^{( хд} М ^ф 3 ^{- ф} 3 ^д м ^х ) ⁺

^{+ е} 2 A М ^{( ф} 2 ^д М ^ф 3 ^{- ф} 3 ^д М ^ф 2 )] ⁺

^{+ g 2 v} [ A М ( A М ^{х — е} 2 A ^{3 ф} 3 )⁺

^{+ е} 2 A М ( A М ^{х +} A М ^ф 2 )]} ^—

—е 1 е 2 2 [ F 1 v ( A ^ A V - A AAV ) +

+ F 2 v ( AA AV — AA AV ) +

+ F³v ( AA AV — AA AV )] ,          (33)

L ^{(4) ( е} ) = ^— 4 ^{х 4 + е 2} 2 { ^— ^^{х 2} ( ^ф 2 ^{+ е 2 ф} 3 ) ^—

^{— е} 1 ^ ( ^ф 2 ^{+ е} 2 ^ф 3 ) ⁺

^{+ g 2} [ ^е 1 ( A М ^ф 2 ^{+ е} 2 A М ^ф 3 ) ⁺

⁺ ( A М ^{х — е} 2 A М ^ф 3 ) ⁺

^{+ е} 2 ( A М ^{х +} A М ^ф 2 ) ] ^—

—е 2 g 2 [ е 2 ( A М A V — AA A ) V ) ² +

+ ( A ^ A V — A A V I ) 2 +

+ е 1 ( A ^ A V — AA AV ) 2 ] J- .           (34)

Полезно отметить, что теории с калибровочной группой Кэли-Клейна SO(3; е) могут быть получены из SO(3) калибровочной теории (формулы (30)-(34) при е 1 = е2 = 1) заменой v → v, χ → χ, ϕ2 → ϵ1ϕ2, ϕ3 → ϵ1ϵ2ϕ3,

A1µ → ϵ1A1µ, A2µ → ϵ1ϵ2A2µ, A3µ → ϵ2A3µ,(35)

или

B1    12     233

µ → ϵ1Bµ, Bµ → ϵ1ϵ2Bµ, Fµν → ϵ2Fµν(36)

для новых полей.

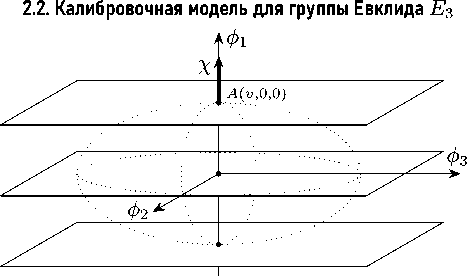
Рисунок 7. Плоскости основных состояний лагранжиана L ( е 1 ) .

Figure 7. Ground state planes of the Lagrangian L ( е 1 ) .

При б 1 ^ 0 ,e 2 = 1 группа SO (3) контрактирует-ся в неполупростую группу Евклида E 3 . Метрика в пространстве полей материи вырождается ф * ( б 1 ) ф ( б 1 ) = Ф 1 + б 1 ( ф 2 + ф 3 ) , и Ф ₃ ( б 1 ) становится расслоенным пространством с одномерной базой {ϕ 1 } и двумерным слоем {ϕ 2 , ϕ 3 } (рис. 7). Лагранжиан (30)–(34) преобразуется к виду

L (б 1) = Lb (б 1) + б 1 Lf (б 1) + б 1 Lint(б 1) , где

L b ^{( б} 1 ) = 2^{( д} ^ \ ^{) 2} -^{м 2 х 2} -^^ф о ^{х 3} - 4 ^{х 4} - 4⁽ F pv ^{) 2} ,

L f ( б 1 ) =

— 1Г R1 124 g 2 v 2 CR¹^ Ъ r2 ^² + g 2 v 2 fR2^² +

= - 4⁽ B pv ) ■ ₂ ' B P ) - 4⁽ B v ) ' ₂ ' B ) ⁺

+ L f ³⁾( б 1 )+ L f ⁴⁾( б 1 ) ,

L int ^{( б} 1 ) - ^ ( ^ф 2 + ^ф 3 ) +

+ g ² [( A ^ф 2 2 + A р ^ф з )    ( AP A V - A ² A V ) ] ■ ⁽³⁷⁾

Здесь L f ( б 1 ) дается выражением (33) при б ₂ = 1 без слагаемого —Аф 0 х 3 , а L f ⁴^( б 1 ) имеет вид

^L f ⁴⁾( б 1 ) =

= 2 { ^{— Ах} 2 ( ^ф 2 ^{+ ф} 3 )⁺ g 2 [( A * ^х - A 3^ ^ф з ) ⁺

+ ( A p x + A р ^ф 2 ) ] -

—g ² [( A I A V — A I A V ) 2 + ( A I AI — A I A V ) 2 ] } ■

Лагранжиан в базе Lb(б 1) описывает хиггсовский бозон X со стандартной массой mx = ^/2м, его самодействие и безмассовое векторное поле A3µ. Лагранжиан в слое Lf (б 1) описывает два массивных векторных поля Bp, Bp (32) с одинаковыми массами mB = gv и различные взаимодействия полей. Помимо этого, контрактированный лагранжиан L(б 1) содержит слагаемые, пропорциональные ϵ41, которые отвечают взаимодействию полей четвертного порядка.

Как и в случае калибровочной группы SO (2; б ) , за счет калибровочных преобразований, связывающих вакуум в точке A ( v, 0 , 0) с полями ф 2 , ф 3 , можно преобразовать лагранжиан L ( б 1 ) к виду, содержащему только калибровочные поля B µ ¹ ,B µ ² ,A ³ µ , поле хиггсовского бозона χ и взаимодействия между ними.

Представления (37), (38) описывают порядок стремления к нулю слагаемых в лагранжиане при переходе к пределу б 1 ^ 0 . Вначале считаем малым и пренебрегаем лагранжианом L _int ( б ₁ ) , далее малым будет лагранжиан L f ( б 1 ) , окончательно получаем лагранжиан в базе L b ( б 1 ) . Можно рассматривать и обратный процесс восстановления полей и взаимодействий при изменении параметра контракции ϵ ₁ от нуля до единицы.

Теория с калибровочной группой Евклида E2 может быть получена из SO(3) калибровочной теории (формулы (30)-(34) раздела 2.1 при б 1 = б2 = 1) заменой v →v, χ → χ, ϕ2 → ϵ1ϕ2, ϕ3 → ϵ1ϕ3,

B 1 12 23 3

_µ → ϵ 1 A _µ , B _µ → ϵ 1 A _µ , A _µ → A _µ (39)

с последующим переходом к пределу б 1 ^ 0 .

Если выбрать основное состояние, отвечающее точке B (0 , v , 0) на рис. 6, где ф 1 = 0 , то в пределе б 1 ^ 0 его группой инвариантности окажется подгруппа SO (2) , рассмотренная в разделе 1.

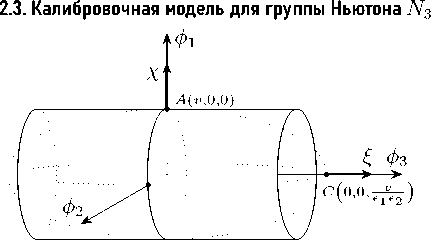
Рисунок 8. Цилиндр основных состояний лагранжиана L ( е 2 ) .

Figure 8. Cylinder of ground states of the Lagrangian L ( е 2 ) .

При б 1 = 1 ,б ₂ ^ 0 группа вращений SO (3) контрактируется в неполупростую группу Ньютона N ₃ . Метрика в пространстве полей материи вырождается ф * ( б 2 ) ф ( б 2 ) = ф 1 + ф 2 + б 2 ф 3 , и Ф 3 ( б 2 ) становится расслоенным пространством с двумерной базой {ϕ ₁ , ϕ ₂ } и одномерным слоем {ϕ ₃ }. Лагранжиан модели

L (б 2) = Lb (б 2) + б 2 Lf (б 2)

состоит из лагранжиана в базе

1                     1

L b ^{( б} 2 ) = 2^{( d} ^ ^X ) - ^{М X} - 4^{( B} ^v ) '-- 2 ' B p. ) +

+L b3)( б 2)+ Lb4)( б 2),(41)

который описывает хиггсовский бозон χ, массивный бозон B ¹ и взаимодействия вида ^µ

L b ^{3)( б} 2 ) = ^{— A}vx ³ - ^Аvх^ф 2 + gA p ⁽ х^д Р ^ф 2 - ^ф 2 ^д р х ) ,

L ь *4⁶ 2 ) — - 4 ^{x 4} + g^ ^{x 2 (} A 1. ^{) 2} - 2 ^{x 2} @ 2 +

+ у ф 2 ( A m ) 2 -1ф 2             (42)

и лагранжиана в слое

L f ( < 2 ) — - 4( f M v ) ² - 4( B 2 v ) ² + 7( B 2 ) ² +

⁺ L f ^^{( 6} 2 ) ⁺ Lf \⁶ 2 ) ,              ⁽⁴³⁾

где

L f³\⁶ 2 ) ^— | ^— А«^хф 2 ⁺

⁺ 9 [ ^A M ^{( xd} M ^ф 3 ^{— ф} 3 ^d M ^X ) ^{+ A 3 ( ф} 2 ^д м ^ф 3 ^{— ф} 3 ^д м ^ф 2 )] ^{+ + 9 2 ф} о ^{A 2} ( ^{A 2 x + A З ф} 2 )

⁹ [ T’¹ ( Д²Д³    Д³ Д² ) T’² ( Д3Д¹    Д¹ Д³)

2 F Mv (^AM ^A v ^A ^ ^A v) ⁺ F mv A^v ^A M ^A v) ⁺

B или C на рис. 6, попадающих в пределе в слой, то получаем калибровочные модели, отвечающие соответствующим двухпараметрическим подгруппам исходной калибровочной группы.

3. Калибровочные теории с группами SU(2; е)

Унитарная контрактированная группа SU (2; 6 ) определяется как группа преобразований комплексного пространства C ₂ ( 6 ) , оставляющая инвариантной квадратичную форму

ф ( 6 ) ^ ф ( 6 )— |ф 1 ( 6 ) | ² + 6 ² |ф 2 ( 6 ) | ² ■         (46)

Преобразования комплексных полей имеют вид

^ф' ^{( 6} ) ^— u ^{( 6} ) ^{ф ( 6}, )

( ф 1 ( 6 )  ) _— ( а (_ 6 )     6в ( 6 ) ) ( ф 1 ( 6 )  )

\ ^6ф 2 ^{( 6} ) )     \ ^{—6в ( 6} )    ^{а ( 6} )  / \ ^6ф 2 ^{( 6} ) ) ’

⁺ F Mv ( ^A M ^A V ^{- A} M ^A V )] I ’

det и ( 6 ) — 1а ( 6 ) | ² + 6 ² 1в ( 6 ) | ² — 1 , и ( 6 ) U ( 6 ) — 1 ■

Генераторы группы SU (2; 6 ) даны матрицами

L f ^{4)( 6} 2 ) ^— 2 | ^- ^^ф 3 ( ^{X 2 + ф} 2 ) ⁺

^{+ 9 2} [( ^A M ^{x + A} М ^ф 2 ) ^{+ 2 A} M ^A М ^ф 2 ^ф 3 ^{— 2 A} M ^A М ^хф 3 ] ^—

T — 6 1(0 1      т^ — 6 ¹

1     2 \ 1 0 / ’    2     2 \ т3—2 (0 —1)’

-i

i

,

^{- g 2} [( ^A M ^A v ^{— A} M ^A v ) ⁺ ( ^A M ^{A 2 — A} M ^A v ) ]} ■

(44) Таким образом, лагранжиан в слое содержит безмассовое поле A ³ _µ , массивное поле B _µ ² и взаимодействия полей.

Отметим, что лагранжиан L b ( 6 ₂ ) в базе (41), (42) описывает те же поля, что и лагранжиан L ( 6 — 1) (7) модели с калибровочной группой SO (2) . Отличия в слагаемых, отвечающим взаимодействиям третьего и четвертого порядков, исчезают при избавлении от ϕ 2 путем перехода к полю B _µ ¹ аналогичного переходу от B µ к B µ .

Теория с калибровочной группой Евклида N 2 может быть получена из SO (3) калибровочной теории (формулы (30)-(34) раздела 2.1) при 6 1 — 6 ₂ — 1 ) заменой

подчиняются коммутационным соотношениям

[ T 1 ,т 2 ] — i6 ² T 3 , [ T 3 ,т 1 ] — iT 2 , [ T 2 ,т 3 ] — iT 1

и образуют алгебру su (2; 6 ) .

В калибровочной теории с группой SU (2; 6 ) калибровочные поля

Am(x; 6) — g^TkAM(x) — k=1

-q V ^A M      ^{6 ( A} M ⁺ i^A M О   (5Q)

— 92 у 6(AM — iAI)     —AM принимают значения в алгебре Ли su(2; 6). Ковариантные производные равны

v →v, χ → χ, ϕ 2 → ϕ 2 , ϕ 3 → ϵ 2 ϕ 3 ,

A ¹ µ → A ¹ µ , A ² µ → ϵ 2 A ² µ , A ³ µ → ϵ 2 A ³ µ     (45)

с последующим пределом 6 ₂ ^ 0 .

Аналогично разделу 1, в калибровочной теории с группой SO (3; 6 ) при 6 k — 0,k — 1 , 2 в качестве вакуума можно выбрать любое основное состояние на эллипсоиде рис. 6. Однако, для того, чтобы получить теорию с полной трехпараметрической контрактированной группой Евклида E ₃ или Ньютона N з при переходе к пределу 6 1 ^ 0 , 6 ₂ — 1 или 6 1 — 1 , 6 ₂ ^ 0 , необходимо, чтобы выбранный вакуум (скажем, точка A на рис. 6) в соответствующем пределе принадлежал базе расслоенного пространства (рис. 7 или 8). Если же вакуум модели выбран, например, в точках

^D м ^{ф ( 6} ) ^{— д} м ^{ф ( 6} )

-

i9 (Е ^T k ^am]

ф ( 6 ) ,

где константа g является зарядом. Тензоры напряженности калибровочных полей определяются формулами

A mv ( x ; 6 ) — A m„ ( x ; 6 ) + 9 [ A m ( x ; 6 ) ,A „ ( x ; 6 )] ,

A ^kM„ ( x ; 6 ) — д м А^к „ ( x ; 6 ) — d v A M ( x ; 6 ) ■     (52)

Вместо полей (50) вводятся новые калибровочные поля Z M ^{( x} ) ^{— A} M ^{( x} ) ’

W ± ( x ) — 67 2 ( A M ( x ) * iA M ( x )) ’      (53)

которые в случае электрослабой модели имеют непосредственный физический смысл.

Лагранжиан модели L ( е ) = L A ( е ) + L ф ( е ) представляет собой сумму лагранжиана калибровочных полей

L a ( е ) = - 4 {[ е ² ( A 'v ) 2 + ( A %, ) 2 ] + ( A J, ) ² } (54) и лагранжиана полей материи

LФ(е) = 2(djФ(е))]^ф(е)- V(Ф;е)■

Основные состояния лагранжиана L ( е ) обнуляют калибровочный лагранжиан L A (е ) = 0 и доставляют минимум потенциалу

• V (Ф; е) = 4 (ф4(е)Ф(е) - v2) ■(56)

Эти состояния задаются уравнением

Ф1 + Ф 2 + е 2( ф 3 + ф 4) = V2,(57)

которое описывает трехмерный эллипсоид (сферу при е = 1 ) в четырехмерном пространстве Ф ₄ ( е ) вещественных полей ф к , k = 1 , 2 , 3 , 4 , где ф 1 = ф 1 + iф 2 , ф 2 = ф 3 + iф ₄ . Данный трехмерный эллипсоид можно мыслить себе как поверхность, изображенную на рис. 6, если подразумевать под ф ₃ двумерную плоскость, натянутую на ф ₃ ,ф ₄ , и положить ф 1 = ф 1 , ф ₂ = ф ₂ .

При е = 0 все основные состояния могут быть получены калибровочными преобразованиями из одного из них. Как и в случаях калибровочных моделей с ортогональными группами, рассмотренных в разделах 1 и 2, для получения калибровочной теории с трехмерной контрактиро-ванной унитарной группой, нужно вакуум модели выбрать в точке, попадающей в пределе е ^ 0 в слой пространства Ф 4 ( е ) .

Из соображений простоты вакуумный вектор можно взять в виде (фvac)4 = (v, 0), т. е. ф 1 = v,ф2 = ф3 = ф4 = 0 (точка A(v, 0, 0, 0) на эллипсоиде (57), рис. 6). После этого рассматриваются малые (линейные) возбуждения поля ф1 в окрестности вакуума ф 1( x )= V + х (x), ф 2 (x), ф 3( x), ф 4( x)■ (58) Для нового поля ф(x) полный лагранжиан модели принимает вид

L ( е ) = L ⁽²⁾ ( е ) + L in ( е ) ,            (59)

где, как обычно, квадратичные по полям слагаемые лагранжиана L ⁽²⁾ ( е ) описывают свободные частицы модели, а слагаемые более высокого порядка L in ( е ) рассматриваются как их взаимодействия. Квадратичный лагранжиан

L ⁽²⁾ ( е ) = L 0²⁾ ( е )+ е ² L 22) ( е ) ,

L 02) ( е ) =

= 2 ^{( d} J ^x )   2 ^т х ^х   4 Z J, Z J, ⁺ 2 m z Z J Z J ,

L ⁽²⁾ ( е ) = - ¹ W + W - + m ²_W W. ^- W -^-   (60)

µν µν         µ µ включает скалярное поле Хиггса х с массой mx = a/2Av, нейтральную Z и заряженные векторные частицы W± с одинаковыми массами mz = mW = 2gv. Лагранжиан взаимодействия имеет вид

L ^int ( е ) = L

int

1   2 iint 1   4 iint

+ е l 2 + е l 4 , int

- ^A х ⁴ - Avx ³ +

gm z

2 cos G W

^{х ( Z} j ^{) 2} +

g ²

⁺ 8 2Д ^{X ( Z} J ) ’ 8 cos ² G W

L in = gxw + w ^- + g ² х ² w - w - -

• -    2 ig ( W J W - - W ^- W - ) Z jv cos G w -

• -    ig cos G w [ Z . ( W + , W - - W ^-, W  -

• - Z , ( W+ W ^- - W ^-, W j -)] -

• - g^cos Gw{ [(W^-) + (W-)](Z, )2 - -2 (W^-W- + W--W-) Z Z + + [(W,+)2 + (W-)2] (Zj)2} ,

L 4 ^nt = g ² ( W^- W - - W -^- W , ⁺ ) ² ■      (61)

Как и в случае ортогональных групп Кэли-Клейна, теорию с унитарной калибровочной группой SU (2; е ) можно получить из SU (2) калибровочной теории (формулы этого раздела при е = 1 ) заменой

• ^v ^ ^v, х ^ х, ^ф 1 ^ ^ф 1, ^ф2 ^ ^еф2,

4. Заключение

Z →Z , W ^± → ϵW ^± .        (62)

Замечание . В стандартной электрослабой модели [8] с калибровочной группой SU (2) х U (1) в качестве вакуума выбирают поле ф V_ac = (0 ,v ) , т. е. ф ₃ = v,ф 1 = ф ₂ = ф ₄ = 0 (точка C (0 , 0 ,v, 0) на эллипсоиде (57), рис. 6). При е = 1 такой выбор приводит к тем же массам калибровочных полей, что и выбор поля ( ф^{т с} ) ⁴ = ( v, 0) , отвечающего точке A ( v, 0 , 0 , 0) . Однако он не согласован с контракцией е ^ 0 . Правильные преобразования полей электрослабой модели при контракции даются формулами (62), как это сделано в работе [12].

Контракции ортогональных и унитарных групп Кэли-Клейна и расслоения соответствующих пространств фундаментального представления тесно связаны между собой. Расслоенные пространства имеют вырожденную метрику и целый набор инвариантов относительно контрак-тированной группы [11]. Это означает, что в калибровочных теориях с контрактированными группами Кэли-Клейна пространства полей материи являются расслоенными пространствами. Для полного описания поведения физических систем в процессе предельного перехода необходимо рассматривать полное выражение для лагранжиана, в том числе и его зависимость от параметра контракции, а не только предельные лагранжианы в базе и слое. Это позволяет проследить порядок обнуления слагаемых в лагранжианах при стремлении параметров контракции к нулю, а также восстановление лагранжиана при обратном процесе – деформации.

Важное значение имеет выбор вакуума в механизме спонтанного нарушения симметрии. Чтобы получить теорию с полной контрактированной группой, имеющей ту же размерность, что и исходная калибровочная группа, необходимо, чтобы выбранный вакуум в соответствующем пределе принадлежал базе расслоенного пространства полей материи. Только в таком случае в контрактированной калибровочной теории получается тот же самый набор полей и частиц с теми же самыми массами, что и в исходной теории. Выбор вакуума, попадающего в пределе в слой, приводит к калибровочной модели, отвечающей подгруппе исходной калибровочной группы.

Поскольку именно структурные константы ответственны за взаимодействие полей и поскольку при контракциях групп Ли часть структурных постоянных их алгебр обращается в ноль, калибровочные теории, основанные на кон-трактированных неполупростых группах, описывают более простые взаимодействия полей, чем исходные теории, отвечающие простым или полупростым калибровочным группам.