Контракции супералгебр и неоднозначность диаграмм Дынкина

Суперсимметрия продолжает оставаться объектом интенсивного изучения в математической физике. Обобщение математических объектов на их супераналоги — суперфункции, супералгебры, суперпространства — приводит к красивым результатам и в физике, и в математике [2, 3]. Контракция [4] представляет собой математическую операцию, которая связывает неизоморфные алгебры Ли. Контракции, приводящие к супералгебрам Пуанкаре и Галилея, находят применение в теории суперструн и суперконформных теориях поля. В данной работе мы покажем необычное поведение супералгебр Ли при контракциях и опишем действие супергруппы Галилея на флаговых суперпространствах R ² 1 1 ( j 1 , j ₂ ) и ^{R 1 1 2 (} j 1 ^,j 2 ) .

1. Супералгебры Ли

Линейное пространство V называется суперпространством, если оно наделено Z ₂ -градуировкой, т.е. разложением V = V ₀ ф V 1 . Элементы V ₀ называются четными, а V 1 — нечетными.

Линейные преобразования суперпространства описываются суперматрицами. Суперматричной структурой или просто суперматрицей называют матрицу с приписанной каждой строке и столбцу четностью. Обычно суперматричная структура выбирается так, чтобы четные строки и столбцы шли сначала, а

нечетные — потом. Такая структура называется стандартной. Например, первая матрица имеет стандартную структуру, вторая — нестандартную.

I

Ч

Ч

Н

Ч

Ч

Н

Н_Ч    ,     Н_Ч

Н

Ч Н

Ч Н

Ч

.

Оператор p определяет четность однородных элементов p ( Ч ) = 0 , p ( Н ) = 1 . Супералгеброй A называется суперпространство, снабженное четным гомоморфизмом или суперумножением A⊗A→ A . Супералгеброй Ли называется супералгебра g с умножением, обозначаемым [ , ] (суперкоммутатор), которое удовлетворяет условиям:

[Х,У ] = -(- 1) p(x) p(y)[ У,х],                    (2)

[x, [y,z]] = [[x,y] ,z] + (-1)p(x)p(y) [y, [x,z]] .

Далее коммутатор двух нечетных элементов будем обозначать фигурными скобками {x,y} = xy + yx . Корневые системы, матрицы Картана и классификация супералгебр Ли приведена в работах [5, 6].

Пусть Л = Л _о ф Л 1 — алгебра Грассмана над полем K = R или C , где Л _о — ее четная часть, Л 1 — нечетная. Супергруппу определяют экспоненциальным отображением супералгебры G ~ ехр(Л ₀ A ₀ + Л 1 A 1 ) [2,3,6]. Рассмотрим множе-

ство ( m + n ) x ( m + n ) суперматриц вида

M = ( A B\         (3)

Генераторы можно реализовать трехмерными матрицами

где A, B,C, D — матрицы m x m , m x n , n x m и n x n соответственно. Элементами матриц A и D являются числа из Л ₀ , элементами матриц B и C — числа из Л 1 . Общей линейной супергруппой GL ( m|n ; K ) называется множество обратимых матриц M с обычной операцией матричного умножения.

Приведем примеры представлений суперматрицами некоторых супералгебр Ли. Специальная линейная супералгебра Ли sl ( m|n ) имеет суперматричную структуру

( A 0 ^B 1

B ₀ A ₁

1 2 H =  0 0	0 1 2 0	0 0 , 0	Z =	1 2 0 0	0 1 2 0	0 0 1
0 E + =  0 0	1 0 0	0 )■	E - =	( 1	0 0 0	0 0 0
0 F + =  0 0	0 0 1	0 )■	F - =	( 1	0 0 0	0 0 0	)
0 F' + =   0 0	0 0 0	0 )	F - =	( 0	0 0 0	0 1 0	)

,

,

,

Матрица Картана и диаграмма Дынкина выглядят так

.

где A 0 и A 1 — четные блоки c Tr( A 0 ) = Tr( A 1 ) , размерности m x m , n x n соответственно, а B ₀ и B ₁ — нечетные блоки размерности m x n , n x m соответственно. Простейшая супералгебра sl (1 | 1) с матрицей Картана a = 0 и диаграммой Дынкина 0 задается следующими коммутаторами

[ H,E ]=0, [ H,F ]=0, {E,F } = H, (5)

и представляется двумерными матрицами

H = ( 0 1 ) ,E = ( 0 0 ) ,F = ( 1 0 ),

(6) где генератор H — четный, а E и F — нечетные. Суперматричная структура и градуировка суперпространства ( x, 0) t выглядят соответственно

-2

-1

,

.

Данное представление соответствует стандартной суперматричной структуре. Нестандартная суперматричная структура

/ H + 2 Z	F +	E +
F -	Z	F +
E -	Р1 -	-H + 2 Z )

НЧ

задает изоморфную алгебру с другой матрицей Кар-

тана и диаграммой Дынкина

( -01 10 ) ,

Имеется еще одна суперматричная структура

Н^{Ч Н}Ч    ,        Н^Ч    .            (7)

I

Ч Н Н

Н

Ч

Ч

Н

Ч

Ч

,

Супералгебра sl (2 | 1) та sl (1 | 2) содержит четыре четных генератора E ⁺ , E ^- , H , Z и четыре нечетных F ⁺ , F ^- , F ⁺ , F ^- . Суперматричная структура, градуировка суперпространства и коммутаторы приведены ниже

которая также задает изоморфную алгебру

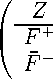
F ^-

H + 2 Z

E ^-

F ⁺

E+      ,

2 Z - H )

^Н Ч_Ч     . (13)

/ H + 2 Z   E+

E-  -H + 1Z

F ^-       F ⁺²

_F +        _Ч

F ^-     , Ч , (8)

Z Н

Меняя суперпространство R ^{2 | 1} на R ^{1 | 2} , имеем еще три реализации алгебры sl (1 | 2) .

[ H,E ± ] = ±E±, [ H,F ± ] = ± 2 F ±,

Z	F -	F +
11 +	h + 2 z	E +
F -	E -	2 Z - H

[ H,F ± ] = ± 2 F ±, [ Z,F ± ] = - 2 F ±,

[ Z, H ] = [ Z,E ±]=0, [ Z, F ± ] = j F ±,

[ E ±, F ± ] = [ E ±, F ± ] = {F ±, F ±} = {F ±F ±} = 0,

( H + 2 Z	F +	E +
F -	Z	F +
E -	F -	2 Z - H)

{F±,F' } = {F±F ' } = 0, {F±,F±} = E±,

H + 2 Z E -	E + 2 z - н	F + F -
F -	F +	Z

НН

(if)

( Н )

[ E±,F ^ ] = -F ±, [ E ±,F ^ ]= F ±,

[ E+ ,E-]=2 H, {F ±,F ■} = Z т H. (9)

Коммутационные соотношения sl (1 | 2) будут задаваться формулами (9), как и в случае sl (2 1 1) .

Супералгебры Ли, как мы видим, имеют, вооб-

ще говоря, много неэквивалентных корневых систем

и, соответственно, матриц Картана и диаграмм Дын-кина, что связано с возможностью выбора различных суперматричных структур. Далее мы увидим, что контракции снимают это вырождение.

[ Hi,Ej] = aij Ej,  [ Hi ,Fj] = - aij Fj ,

[Ei,Fj]= 5ijHj,  i,j = 1, 2,

2. Флаговые контракции

При определении супералгебр сначала вводится понятие Z ₂ – градуировки и суперматричной структуры. Затем при определении коммутаторов градуировка существенно используется. При определении алгебраических контракций похожим способом сначала вводится некоторая матричная структура и затем определяются коммутаторы [4].

Пусть каждый элемент матрицы домножен на некоторую комбинацию произведений параметров j 1 , j 2 ,..., jn . Будем называть это j— структурой. Далее везде j 2 = 0 , 1 .

Флаговой j – структурой вектора назовем структуру вида ( x 1 , j 1 x 2 ,j 1 j 2 x 3 ) t . Набор таких векторов составляет флаговое пространство R ³ ( j 1 ,j 2 ) . Будем называть j – структуру стандартной, если все элементы однородны и рост числа сомножителей параметров происходит сверху вниз. Флаговой j – структурой матрицы назовем такое расположение параметров j , которое сохраняет флаговую j – структуру вектора

(—2 21) ■ ■

Структура ее флаговых контракций получается домножением корневых векторов E ₁ и E ₂ на параметры j ₁ и j ₂ соответственно. В матричной реализации это выглядит как (17). При этом правые части

некоторых коммутаторов домножаются на квадраты параметров.

^a 11 j ₁ a ₂₁ j 1 j 2 ^a 31

j 1 ^a 12 a ₂₂ j 2 ^a 32

j 1 j 2 ^a 13 j ₂ a ₂₃ ^a 33

)

[ E з ,Fз] = j 2 j 22 Hз, [ Ei,Fi ] = ji Hi,

[Ei, F3] = j22 Fз-i, [Ei, Fi] = j2Hi, i,j = 1, 2.

Коммутаторы (22), содержащие элементы матрицы Картана a _ij , не меняются. Обозначим такую алгебру диаграммой Дынкина с приписанными метками j 1 и j 2

j 1      j 2

.

Таким образом, флаговые контракции описывают класс неполупростых алгебр с прежними матрицами Картана, но с помеченными диаграммами Дын-кина.

Рассмотрим нестандартную флаговую j – структуру вектора ( x 1 ,j 1 j ₂ x ₂ ,j 1 x ₃ ) t . Соответствующая j – структура матрицы имеет вид

Для однородных элементов вектора и матрицы введем оператор J , определяющий j – структуру данного элемента. Например:

J ^{( j} 1 ^j 2 x з ) = ^j 1 ^j 2 , J ^{( j} 1 a 12 )= ^j 1 .     ⁽¹⁸⁾

Флагово контрактированной алгеброй Ли назовем алгебру Ли с введенной в реализующие ее матрицы флаговой j – структурой и новым ее коммутатором, определяемым формулами

_ J (A j ) J (В j )

^{[ A,B} | new = т/ГЛ \ ^{[ A, B ]} old ’     ⁽¹⁹⁾

J ([A,B] J )

где A _J , B _J – генераторы, домноженные на j 1 j 2 . . .j n .

a 11 j 1 j 2 ^a 21 j ₁ a ₃₁

j 1 j 2 a 12 ^a 22 j ₂ a ₃₂

j 1 a 13 j 2 ^a 23 a ₃₃

)

Можно рассматривать контракции, индуцированные такими j – структурами, однако легко видеть, что при этом получаются алгебры, изоморфные выше описанным. На языке диаграмм Дынкина этот факт выглядит следующим образом:

j 1

α 1

α 2

j 2      j 1

—a 2 а 1 + а - 2

и соответствует группе автоморфизмов диаграммы и равноправию корней ±a 1 , ±a ₂ , ±a 1 ± a ₂ .

3. Контракции классических алгебр sl(2), sl(3)

Алгебра sl (2) с матрицей Картана a = 2 и диаграммой Дынкина Q задается коммутаторами

[H, E] = 2 E, [H, F] = — 2 F, [E, F] = H.

Контракция получается умножением корневого вектора на j ₁ . При этом правая часть последнего коммутатора домножается на j ₁ ² . Будем обозначать такую алгебру диаграммой Дынкина с меткой j ₁

j 1

.

Более содержателен пример алгебры sl (3)

4. Флаговые контракции супералгебр

Рассмотрим супералгебру sl (2 1 1) в стандартной суперматричной реализации. Введем стандартную флаговую j – структуру (17). Часть коммутаторов (9) сохранится, а часть изменится. Изменившиеся коммутационные соотношения контрактирован-ных супералгебр имеют вид:

[E+, F-] = — j2F+, {F-, F^+ } = j2 j22(Z + H),

[ E-,F+]= j 2 F -, [ E + ,E - ]=2 j 2 H,

H 1

F 1

F 3

E ₁

H ₂ — H ₁

E ₃

E 2

—H ₂

)

{F±, F±} = j22E±, {F+ ,F-} = j22(Z - H).

Диаграмму Дынкина для (25) будем обозначать

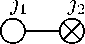
Поменяем теперь расстановку параметров j 1 , j 2 . Нестандартная j – структура плюс стандартная суперматричная структура дают (11)

/ H + 2 Z  j 1 j 2 E+ jij2 E- -H + 2 Z j1F-     j2F+

j 1 F ⁺            x 1

j 2 F ^-     ,       j 1 j 2 x 2     .

Замена 2 о 3 столбцов и строк приводит к обычной расстановке j со второй матрицей Картана

5. Преобразования Галилея в суперпространствах R ^{2 1} 1 ( j 1 ,j 2 ) и R ^{1 1 2} ( j 1 ,j 2 )

Обычно группы Галилея и их действие получают процедурой контракции [4]. Мы, однако, воспользуемся тем, что в (9) уже есть три подалгебры Галилея, действие которых можно получить просто вводя на суперпространствах флаговую структуру.

Рассмотрим подалгебру (25), натянутую на генераторы {E - , F - , F ⁺ } , соответствующую нижнетреугольной части матрицы (8)

H + 2 Z j1F+ j1j2E+ j1F- Z j2F+ j1j2E- j 2 F" - 2 z - h x1

,                                                          • j1j2x2

[ E ^- ,F ⁺ ] = -F ^- , {F ^- ,F ⁺ } = 0 ,

[ E ^- ,F ^- ] =0 , {F ± ,F ± } = 0 *    ( ³¹⁾

Таким образом, нестандартная j – структура

плюс стандартная суперматричная структура есть стандартная j – структура плюс нестандартная суперматричная структура. Опять приведем только изменившиеся коммутационные соотношения:

Введем флаговую структуру (17) ( x 1 ,j 1 x 2 ,j 1 j 2 ©) t . Тогда преобразование координат флагового пространства R ² 1 1 ( j 1 ,j ₂ ) под действием соответствующей подгруппы G = exp( vE ^- + a 1 F ^- + a ₂ F ⁺ ) с четным параметром v и нечетными a 1 , a 2

[ E + , F ^- ] = -j 2 F + , {F ^- ,F + } = j 2 ( Z + H ) ,

[ E ^- ,F + ] = j 2 F ^- , [ E + , E ^- ] = 2 j 2 j 2 H,

[ E + ,F ^- ] = j 2² F + , [ E ^- , F ⁺ ] = -j ₂ ² F ^- ,

{F + ,F " } = j ₂ ² ( Z - H ) *         (28)

x'1 = x 1, x2 = x 2 + vx 1,

Далее выделим подалгебру в (28), соответствующую нестандартной суперматричной структуре (11), натянутую на генераторы {E ^- , F ^- , F ^- } .

Диаграмма Дынкина в этом случае принимает вид: j 1      j 2

Еще одна возможность задается матрицами (12 ) и (17). После циклической перестановки строк и столбцов имеем

[ E ^- ,F ^- ]=0 ,        [ E ^- ,F ^- ]=0 ,

{F ^- ,F — } = E ^- ,   {F ^- ,F — } = {F ^- ,F ^- } =0 *

После введения флаговой структуры данная подгруппа G = exp( vE ^- + a 1 F ^- + a ₂ F ^- ) дает преобразования

h + 2 z j 2 E -	j 2 E + - h + 2 z	j 1 F + j 1 j 2 F -
j 1 F -	j 1 j 2 F +	Z

j 1 x 1

, j 1 j 2 x 2      ,

[ E ^- ,F ⁺ ] = -j 2² F ^- , [ E ⁺ , E ^- ] = 2 j 2 H,

x '1 = x 1 ,

Вариант {E , F ⁺ , F } супералгебры Галилея соответствует второй стандартной структуре (12):

[ E ⁺ , F ^- ] = j ₂ ² F + , {F ^- ,F + } = j 2 ( Z + H ) ,

[ E -, + + ]= F ^- , [ E ^- ,F ^- ]=0 , {F + ,F ^- } = 0 , {F ± ,F ± } = 0 *

{F ± , F ± } = j 2 E ± , {F + ,F — } = j 2 j 2 ( Z - H ) *

Если в (30) сделать замены E ± ^ E ¹ , F ± ^ F ^т , F ± ^ F ^т , j 1 о j 2 , H ^ -H , то (30) и (25) совпадут, т.е. они изоморфны, но действия их супергрупп на соответствующих суперпространствах разные. Так как представления супералгеб sl (1 1 2) (14),(15),(16) в точности соответствуют (13),(11),(8), то и их контракции дают точно такие же результаты. Отличие будет только в действии на соответствующее суперпространство.

В отличие от несуперсимметричного случая sl (3) , когда разные j -структуры приводили к изоморфным контракциям, здесь мы имеем неизоморфные контракции или на диаграммном языке:

Как супералгебра Ли этот вариант изоморфен первому, но действие подгруппы G = exp( vE ^- + a 1 F ⁺ + a ₂ F ^- ) на флаговом суперпространстве другое

Проводя аналогичные действия в случае sl (1 1 2) , будем иметь следующие три варианта действия на флаговом суперпространстве R ¹ ' ² ( j 1 , j ₂ )

Г x ' = x, © 1 = © 1 + ax, t © 2 = © 2 + v © 1 + bx,

j 1      j 2         j 2      j 1

0—0 = $$ $$ .

( x ' = x + a © 1 , © 1 = © 1 , t © 2 = © 2 + v © 1 + bx,

Два расширенных трансляциями времени и пространства варианта супералгебр Галилея, один из которых совпадает с (31), описаны в работе [7]. Упоминание о супералгебре Галилея (33) с действиями (34) и (38) и антикоммутатором, равным генератору буста, в литературе нам неизвестно. Выяснение ее физического содержания было бы интересным, поскольку обычно антикоммутатор суперпреобразований равен трансляциям. В качестве иллюстрации необычных свойств этих супералгебр приведем закон сложения скоростей для преобразований (34) для бозонных координат v 12 = v 1 + v 2 + b 1 a 2 , v 21 = v 1 + v 2 + b 2 a 1,

который неаддитивен и некоммутативен.

Приложение

Для удобства, формулы (9),(25),(28) собраны в таблицу.

	(9)	(25)	(28)
[ H,E ± ]	±E ±	±E ±	±E ±
[ H,F ± ]	± 2 F ±	± 2 F ±	± 2 F ±
[ H, F ± ]	± 2 F ±	± 2 F^ ±	± 2 F^ ±
[ Z, F ± ]	-1F ± 2	-1F ± 2	-1F ± 2
[ Z,F ± ]	1 ± 2	1 ± 2	1 ± 2
[ E + ,E - ]	2 H	2 j 2 H	2 j 2 j 2 H
[ E + ,F - ]	-F +	-j 2 F +	-j 2 F +
[ E - ,F + ]	-F —	-F -	-j 22 F -
[ E + ,F - ]	F1 +	1^ +	j 22 F +
[ E - F +\	F1 -	j 2 F" -	j 2 F" -
{ f ± ,f ± }	E -	j 22 E -	E -
{F + ,F - }	Z - H	j 2 ( Z - H )	j 2 ( Z - H )
{F - F + }	Z + H	j 2 j 2 ( Z + H )	j 2 ( Z + H )

Таблица 1: Коммутационные соотношения (9),(25),(28)