Контроль геометрических параметров посадочных мест высокой точности для чувствительных элементов системы управления движением космического аппарата

деталей и сборок, который проводят с помощью шаблонов, занимает значительную часть в измерениях авиационной и космической отрасли. Данная технология контроля отработана и не требует высокой квалификации рабочих, однако она имеет ряд существенных недостатков, так как на каждую группу элементов требуется индивидуальный заготовленный шаблон. Также эта технология не позволяет в полной мере оценить величину отклонения от требований, определенных в конструкторской документации. При каких либо доработках в конструкции изделия необходимо заменять шаблон [2].

Поэтому, в процессе разработки и производства КА выявляется потребность во внедрении экономичных и эффективных средств диагностики и контроля геометрии изделий. Для решения этих задач можно использовать современные измерительные системы. Большая часть данных систем основана на применении оптических методов измерений. Существует несколько видов данных систем: лазерные радары, лазерные трекеры, теодолиты, интерферометры, фотограмметрические измерительные системы, которые можно внедрять на разных стадиях производства [3].

Эти системы сочетают в себе высокую точность, производительность, бесконтактность измерений и получении результата в цифровой форме. Еще одним плюсом данных систем, является их компактность и мобильность, данные системы можно легко разместить в сборочном цехе или производить измерения с выгодных положений, в отличие от координатно-измерительных машин, для которых необходимо размещение измеряемого объекта в рабочей зоне стола прибора [4].

Одним из самых универсальных измерительных средств, применяемых для решения указанных выше задач, являются системы лазерные координатно-измерительные, так называемые лазерные трекеры.

Лазерные трекеры состоят из высокоточных лазерных измерителей расстояний на базе абсолютного дальномера (ADM), и интерферометра (IFM), высокоточных измерительных датчиков вертикального и горизонтального углов и ЭВМ, ADM представляет собой дальномер с инфракрасным источником излучений, который реализует фазовый принцип измерения расстояний. В основе принципа действий IFM, построенного с использованием He-Ne лазера, лежит интерференционный метод измерения расстояний [5].

Программное обеспечение определяет координаты центра элемента, его геометрические параметры и отклонения формы, также возможно контролировать линейно-угловые размеры между измеренными элементами и осуществлять анализ их взаимного расположения (непараллельность, неплоскостность и т.д.). Возможно сравнение криволинейных поверхностей деталей с CAD моделью в программном обеспечении.

На рис. 1 представлена принципиальная схема определения координат отражателя (x0, y0, z0) по результатам замеров горизонтального (Hz) и вертикального (V) углов и расстояния (D) с помощью лазерного трекера. В данном случае определяются координаты отражателя в полярной системе координат трекера, с началом системы координат в точке пересечения осей вращения прибора вокруг своей вертикальной оси и оси вращения подвижной головки. После выполнения измерений на 3 и более контрольные точки объекта с известными координатами, все остальные измерения могут быть автоматически пересчитаны уже в системе координат объекта. Погрешность при измерениях составляет 10 мкм.

Для определения координаты используются данные формулы:

x0=D* cos Hz;

Уо = D* cos(90° - Hz); z0 = D * cos V.

В процессе разработки космического аппарата радиолокационного наблюдения для обеспечения целевых характеристик высокодетального радиолокационного комплекса (ВРЛК) возникла необходимость организации работ по измерению фактического углового положения посадочных мест под чувствительные элементы системы управления движением (ЧЭ СУД) относительно системы координат БА ВРЛК и дальнейшего использования результатов этих измерений в системе управления движением (СУД).

Цель работы – создание методики определения фактического углового положения посадочных мест под установку чувствительных элементов системы управления движением относительно СК БА ВРЛК.

Задачами работы является:

• -    определение координат контрольных точек центра базового отверстия, базового паза и базовой плоскости на раме БА;

• -    определение координат контрольных точек на посадочных местах под установку чув-

  

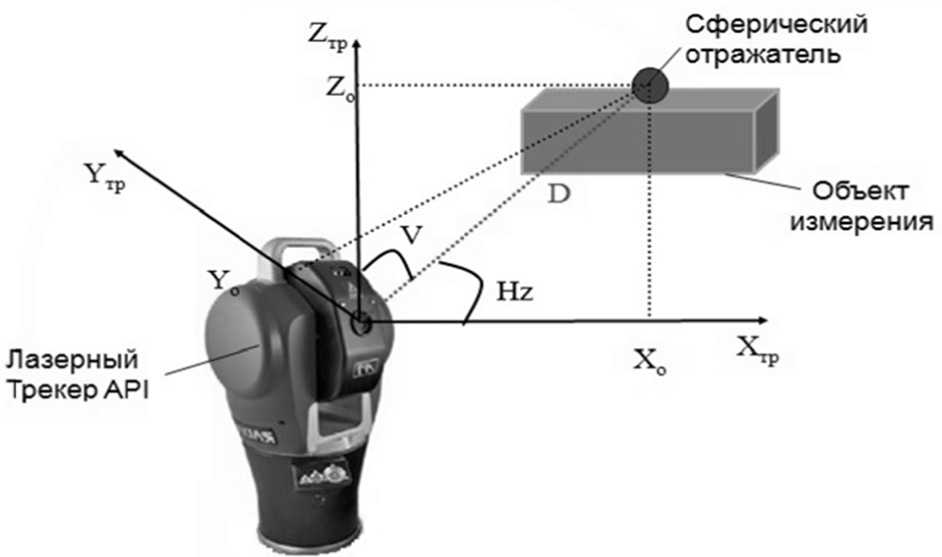
  Рис. 1. Принцип работы лазерной измерительной системы

  
  

ствительных элементов системы управления движением.

Объектом измерения является рама БА ВРЛК с кронштейнами ЧЭ СУД, конструктивная схема которой представлена на рис. 2.

Измерения координат контрольных точек для определения углового положения кронштейнов ЧЭ СУД относительно СК БА ВРЛК должны выполняться лазерным трекером API Radian, путем касания измеряемых элементов поверхностью сферического высокоточного отражателя. Измеряются точки на базовой плоскости, последовательно прикладывая отражатель к поверхности площадок стыковки БА ВРЛК с шагом 5 мм и фиксируя его координаты относительно СК прибора. Далее определяются центр базового отверстия и базовый паз. Измерение положения кронштейнов ЧЭ СУД проводится аналогично, путем последовательного приложения сферического отражателя к каждой из площадок.

После замера всех элементов конструкции следует этап обработки полученных данных.

По окончании измерений в ПО Spatial

Analyzer имеются группы измеренных точек для каждого контролируемого элемента объекта измерений. Анализ углового положения ЧЭ СУД проводится с использованием дополнительных построений по измеренным точкам в следующей последовательности:

• -    создание СК БА ВРЛК в ПО Spatial Analyzer;

• -    создание усредненную плоскость площадки под ЧЭ СУД по точкам, измеренным на ее поверхности;

• -    создание нормали к посадочной поверхности ЧЭ СУД (ось OZПСКi);

• -    создать линию ПOZ1, как проекцию нормали к посадочной плоскости ЧЭ СУД (ось OZПСКi) на плоскость XСКБАВРЛКОСКБА ВРЛК ZСК БА ВРЛК;

• -    определение угла α z, между линией ПOZ1 и осью ОСК БА ВРЛК XСК БА ВРЛК и угла α х, между линией Л1П и осью ОСК БА ВРЛК XСК БА ВРЛК (рис. 3);

• -    определение угла β z, между нормалью к посадочной плоскости «БИУС-М (1)» (ось OZПСКi) и плоскостью XСК БА ВРЛКОСК БА ВРЛКZСК БА ВРЛК (рис. 4);

  Посадочные место под 43 СУД

  

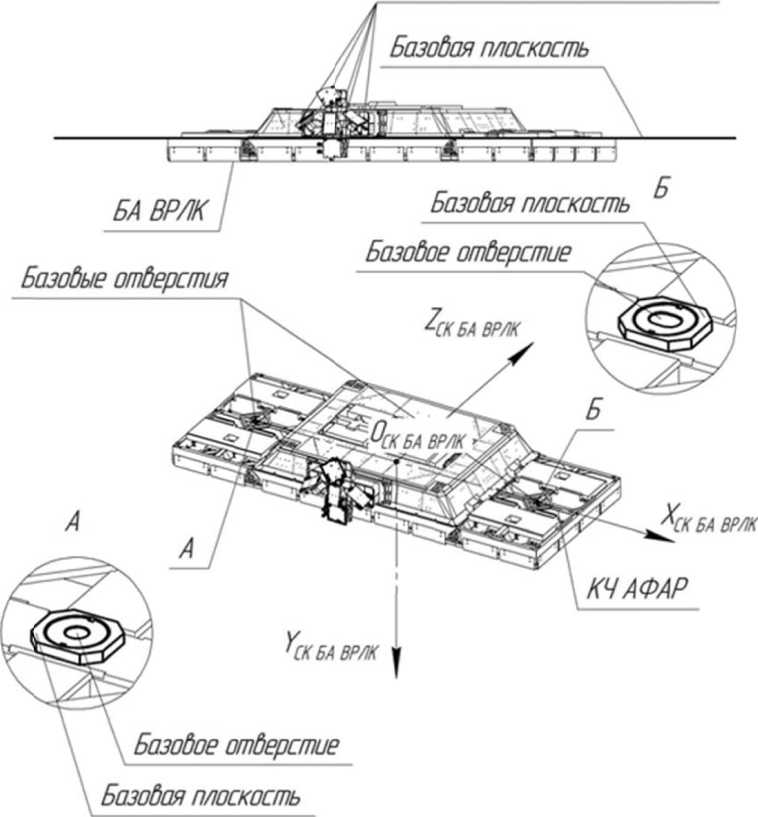
  Рис. 2. Конструктивная схема рамы БА ВРЛК с кронштейнами ЧЭ СУД

  
  

  i L ZtK АЛ ВР/Ж

  

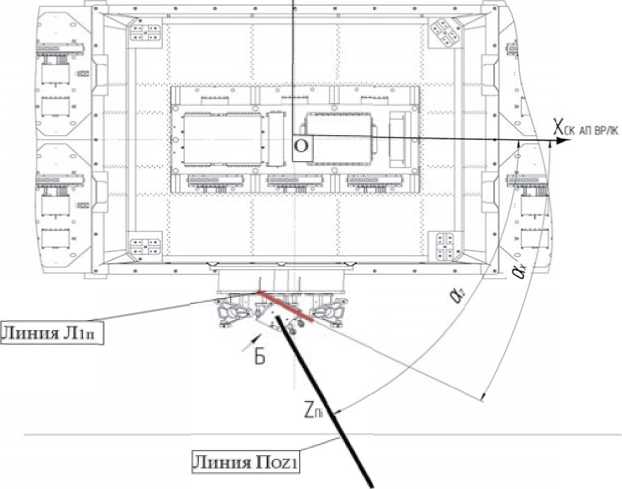
  Рис. 3. Углы az и ax для ЧЭ СУД

  
  
  

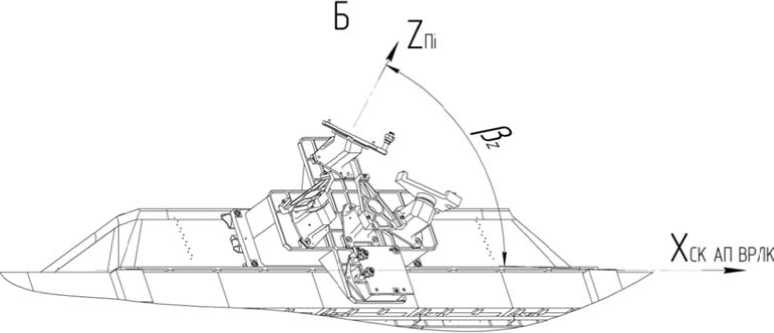
  Рис. 4. Угол p z для ЧЭ СУД

  
  

• -    проведение линии Л1 через центры двух окружностей;

• –    создание проекции линии Л1 на плоскость X СК БА ВРЛК O СК БА ВРЛК Z СК БА ВРЛК, – линии Л1п;

• -    определение угла p x между линией Л1 и плоскостью X СК БА ВРЛК O СК БА ВРЛК Z СК БА ВРЛК (рис. 5);

Предельная погрешность измерения координат определяется измерительной предельной погрешностью лазерного трекера API, погрешностью установки отражателя, а также стабильностью конструкции и опоры.

Оценка погрешности углового положения посадочных мест под приборы проводилась на основе результатов 10 измерений. Полученные значения суммарной погрешности при измерении углового положения посадочных мест под ЧЭ СУД не должны превышать 45ʹʹ.

Оценка измеряемой величины, за которую принимают среднеарифметическое значение измеряемой величины (углового положения посадочных мест под приборы) вычисляется по формуле:

X =

n

Z X.

i = 1 i

n где X – измеряемая величина; n – количество выполненных циклов измерений.

Среднеквадратическое отклонение группы результатов измерений вычисляется по формуле :

5 =

n 2

Zl X,- XI i=1V i j n-1

Доверительные границы случайной погрешности оценки измеряемой величины углового положения посадочных мест вычисляются по формуле:

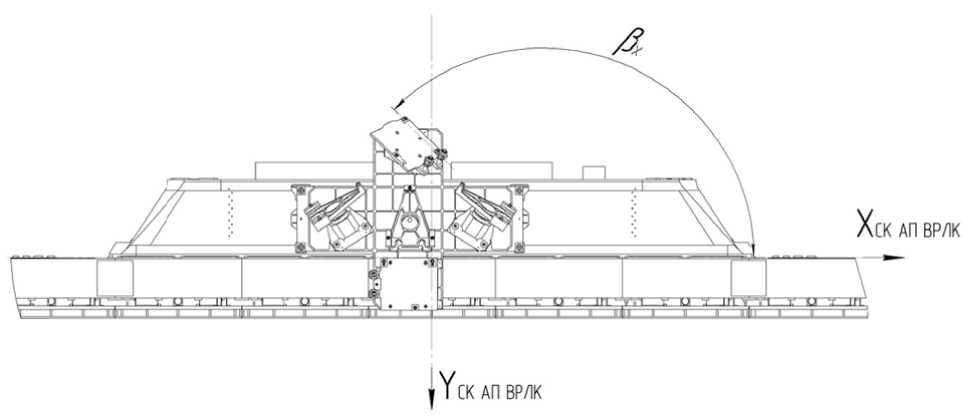
Рис. 5. Угол р х для ЧЭ СУД

А X = t х     ,

n где t – коэффициент Стьюдента, зависящий от доверительной вероятности (P) и числа выполненных измерений (n). Значения приведены в табл. 1

Суммарная погрешность результатов измерений углового положения посадочных мест под приборы вычисля ется по фо рмуле:

Л А = Л XX + 0 x^z, где 0 x - инструментальная погрешность измерений величины углового положения посадочных мест.

Предельная погрешность измерения координат определяется измерительной предельной погрешностью лазерного трекера API, погрешностью установки отражателя, а также стабильностью конструкции и опоры. Погрешность измерений лазерным трекером составляет ±0,005 мм.

Предельная погрешность измерения вертикального и горизонтального угла лазерного трекера API Tracker3, исходя из данных указанных производителем, составляет 0,7 угловой секунды (0,0002 град.), что в линейном выражении составляет 0,0035 мм на метр расстояния между точкой пересечения вертикальной и горизонтальной оси вращения лазерного трекера и центром сферического отражателя.

Величины измеряемого углового положения площадок под приборы и оценка погрешности измерений (при доверительном интервале P=0,997, коэффициент Стьюдента равен 4,03) представлены в табл. 2.

Таким образом, суммарная погрешность измерений не превышает заданной.

ВЫВОДЫ

В данной работе приведены результаты создания методики определения с помощью лазерного трекера фактического углового положения посадочных мест под установку чувствительных элементов системы управления движением относительно системы координат радиолокатора. Выполнена задача обеспечения высокой точности измерений, произведена оценка погрешности измерений, исключена необходимость изготовления сложной технологической оснастки. Результаты измерений будут использованы в системе управлении движением КА.

Таблица 1. Значения коэффициента Стьюдента

n	P
	0,95	0,99	0,995	0,997
6	2,4460	3,7070	4,3160	5,40
7	2,3646	3,4995	4,2293	4,82
8	2,3060	3,3554	3,8320	4,46
9	2,2622	3,2498	3,6897	4,21
10	2,2281	3,1693	3,5814	4,03

Таблица 2. Величины измеряемого углового положения площадок под приборы

Угловое положение площадки	Среднее значение, Град.	Случайная погрешность, град.	Суммарная погрешность, град.	Суммарная погрешность, сек.
	X	Δ X	Δ A	Δ A
a z	61,656	0,0026	0,0027	9,7
P z	62,365	0,0020	0,0021	7,56
a x	26,256	0,0039	0,0040	14,4
p x	134,663	0,0022	0,0023	8,3