Контроль качества нагрева стали в печах по температуре поверхности заготовок в томильной зоне

Постановка задачи

В работах [1, 2] предложены два варианта алгоритма контроля перепада температуры по сечению нагреваемых заготовок в период выдержки при постоянной температуре рабочего пространства в томильных зонах методических печей. Первый вариант алгоритма заключается в контроле перепада Δ по разности температур печи п и поверхности металла пов: Δ =   ( ᴨ - пов), а второй вариант – на основе данных только о мгновенной скорости изменения температуры поверхности металла пов: Δ =     пов, здесь τ – время, а и – некоторые коэффициенты. При этом, что достаточно примечательно, при использовании второго варианта, как это нетрудно заметить, контроль температуры рабочего про странства, при которой осуществляется выдержка, совсем не требуется.

Характерной особенностью алгоритмов является то, что контроль осуществляется по данным текущих измерений независимо от предыстории процесса нагрева.

Оба варианта алгоритма теоретически эквивалентны в том смысле, что с помощью характеристик регулярного режима можно преобразовать один вариант (одну форму записи) в другой (в другую форму записи) и наоборот. При отсутствии каких-либо погрешностей во входных данных оба варианта алгоритма дают абсолютно совпадающие результаты – оценки перепада температуры просто тождественны. Однако влияние имеющих место в действительности погрешностей измерения входных сигналов значимо различное. Так, погрешность измерения температуры поверхности металла, обусловленная наличием поверхностного слоя окалины (в пределах томильной зоны печей это, как правило, практически постоянная величина [3, 4]), оказывает прямое влияние на точность оценки перепада по первому варианту, вместе с тем для второго варианта такая погрешность является малосущественной, так как производная от постоянной величины по времени равна нулю. При этом влияние случайных погрешностей прямо противоположное: на точность оценки по первому варианту это влияние с помощью несложных достаточно известных приемов (например, за счет фильтрации или предварительной аппроксимации реальных данных методом наименьших квадратов, что вообще-то тоже фильтрация) может быть сведено практически к нулю, для второго варианта это влияние является достаточно проблематичным - данный вариант алгоритма весьма чувствителен к случайным погрешностям измерения.

Тем не менее возможность разработки реально работающей подсистемы контроля качества нагрева слябов в печах, инвариантной по отношению к погрешностям, обусловленным наличием поверхностного слоя окалины, является весьма привлекательной задачей при совершенствовании алгоритмического обеспечения АСУ ТП. При этом отметим, что значимость и важность практической реализации такого подхода в АСУ ТП объясняется прежде всего тем, что слой окалины создает существенную систематическую погрешность измерения температуры поверхности неокис-ленного металла. Так, например, в работе [4, с. 222] указано, что в условиях «...выдержки при нагреве металла, характерных для томильной зоны…, перепад на окалине при этом довольно стабилен и составлял 30 °С...». Весомость этой проблемы отмечается также и в работах [3, 5], так, в работе [3, с. 77] подчеркнуто, что «…температура поверхности заготовки может значительно отличаться от действительной температуры поверхности металла из-за наличия на нем слоя окалины», а в работе [5] сообщается, что перепад температуры по толщине окалины может достигать даже и 100 °С. Подчеркнем также, что эта погрешность является абсолютно неустранимой, если только при измерениях не использовать такое сложное и уникальное устройство, как пирометр Лэнда [3]. Однако с его помощью возможны только разовые измерения, согла- сованные с движением слябов в печи. Кроме того, прибор по некоторым причинам необходимо после каждого измерения выводить из рабочего пространства печи. Разовые измерения возможны также и с помощью контактных термопар, вводимых в рабочее пространство печи через ее смотровые окна.

Таким образом, необходима разработка приемлемого для практики алгоритма дифференцирования сигнала о температуре поверхности нагреваемых слябов в условиях томильных зон методических печей. Это и позволит создать вышеупомянутую подсистему контроля качества нагрева металла в печах, которая, следует это особо подчеркнуть, будет инвариантной как по отношению к реальной толщине окалины, так и по отношению к фактическому перепаду температуры в ней.

Анализ процедур дифференцирования промышленных сигналов

Как это хорошо известно, задача достаточно точной численной оценки производной сигнала со случайной ошибкой является трудно реализуемой, в первую очередь, вследствие ее некорректности [6-9]. Известные в литературе алгоритмы [6–21] базируются на различных идеях и подходах, разработаны эти алгоритмы для конкретных задач и условий и характеризуются разными достоинствами и недостатками. Как указано в работе [22], «…выбор оптимального способа дифференцирования зависит, безусловно, от вида сигнала и характеристик шума». Поэтому напрямую, без дополнительной настройки и оптимизации достаточно сложно воспользоваться тем или иным известным алгоритмом, возникает настоятельная необходимость в разработке конкретного способа реализации процедуры дифференцирования для конкретной решаемой задачи. В связи с этим рассмотрим известные в литературе методы цифрового дифференцирования промышленных сигналов.

Отметим, что широко известны так называемые точечные алгоритмы дифференцирования, например, простейший двухточечный алгоритм имеет вид [10-12, 15, 21]

( ) ( ) ( )

dx ~ Дт ^, ( ) где %(т) - измеряемый сигнал; т - время; Дт -промежуток времени между моментами считывания сигнала Дт = т_+х — тр i = 0,1,2,..., Т = i • Дт.

Известно также, что лучшая точность достигается при использовании двухточечного алгоритма центральной аппроксимации [10, 21]. При этом отмечается, что вообще-то большая точность вычисления производной может быть достигнута при использовании многоточечных алгоритмов [21], в частности, за счет усреднения результатов вычислений производной для двух соседних точек по двухточечному алгоритму с шагом 2Δτ [13, 19].

Кроме того, известны и различные регу-ляризирующие алгоритмы [6–18]. Здесь часто используются алгоритмы, основанные на аппроксимации измеряемого сигнала алгебраическим полиномом с последующим его аналитическим дифференцированием [11, 13–15], так, в частности, в работе [15] применяется кубическая сплайн-аппроксимация измеряемых данных, а в работе [20] использована предварительная локальная скользящая квадратичная аппроксимация дифференцируемых сигналов.

Следует заметить, что регуляризация по сути дела, что, кстати, весьма часто указывается в литературе [см., например, 22], представляет собой подавление (фильтрацию) высокочастотной случайной составляющей погрешности измерения сигнала. Как нам это представляется, и некоторые многоточечные алгоритмы, включающие в свою структуру процедуры усреднения, также следует отнести к регуляризирующим алгоритмам.

В работе [17] для решения задачи дифференцирования используется частотный подход, аппроксимирующая функция с конечным частотным спектром подбирается по свойствам ее производной, здесь регуляризация сводится к минимизации евклидовой нормы оценки производной.

Задачу дифференцирования можно решить и следующим образом [16]. Хорошо известно, что ∫   ( )=  (τ)- (0). Если при этом (0) =0, т. е. если задача приведена к нулевым начальным условиям, что несложно реализовать, то проблема дифференцирования сводится к решению интегрального уравнения ( )                                                ( )

∫      =  (τ) относительно    .

В [12] используются оценки производной, вычисленные по простейшему двухточечному алгоритму (1) с одним и тем же временным промежутком между точками. При этом считается, что на используемом для оценки от- резке времени истинная производная равна одному и тому же значению, т. е. является const. Для отыскания результирующей оценки производной решается система линейных алгебраических уравнений (СЛАУ), отыскивается ее псевдорешение. Установлено, что с увеличением количества частных оценок по соотношению (1) точность результирующей оценки производной увеличивается, однако увеличивается и вычислительная сложность процедуры.

Алгоритм работы [16], базирующийся на решении интегрального уравнения, также является сложным в вычислительном отношении. Близким по сложности к алгоритмам работ [12, 16] следует считать и алгоритмы работ [15, 17], требующие решения СЛАУ.

В работе [18] отмечается, что часто при дифференцировании сигналов востребованы быстродействие методов и возможность их использования в режиме реального времени. Все это, конечно, определяется их вычислительной ресурсоемкостью. Указано, что регу-ляризирующий алгоритм А.Н. Тихонова, в котором решается интегральное уравнение, требует большой вычислительной ресурсоем-кости.

В целом, как это указано в работе [23], «…наиболее распространенные… подходы к задаче численного дифференцирования условно можно разделить на две группы. Первая предполагает предварительное решение задачи аппроксимации… с последующим дифференцированием, …ко второй группе можно отнести синтез оптимальных нерекурсивных широкополосных дифференциаторов». Отмечается также и более детальная классификация подходов [24], тем не менее и эта классификация в общем укладывается в двухвариантное разделение методов. Поэтому вполне целесообразно рассмотреть возможность применения в данном случае подходов, относящихся как к первой, так и ко второй группе алгоритмов дифференцирования.

Примечание 1. Интерполяционный способ представления функций нельзя считать приемлемым в данном случае, так как как случайные, так и систематические погрешности измерений температуры при интерполяции будут обязательно вноситься в интерполяционный полином, что приведет к весьма нежелательной ошибке при последующем дифференцировании.

Оценка применимости метода дифференцирования с предварительной аппроксимацией результатов измерения температуры поверхности сляба

Рассмотрим наиболее предпочтительный и наиболее употребимый подход к решению задачи дифференцирования промышленных сигналов - это посредством предварительной аппроксимации экспериментальных данных подходящей функцией. При этом заметим, что выбор аппроксимирующей функции вообще-то плохо формализуем, хорошо, если известна физика рассматриваемых процессов, тогда структура аппроксимирующей зависимости и выбирается в соответствии с этим знанием. В этом случае аппроксимация экспериментальных данных обычно получается наиболее точной, мера близости расчетных и экспериментальных данных принимает минимально возможное значение. Если же структура аппроксимирующей зависимости подобрана плохо, то задачу аппроксимации нельзя решить должным образом. Поэтому при выборе структуры модели аппроксимации результатов измерения температуры поверхности сляба в томильной зоне печей есть смысл воспользоваться закономерностями регулярного теплового режима, как это и было сделано при разработке самих алгоритмов контроля.

Как известно, изменение температуры поверхности сляба на стадии выдержки в томильной зоне методических печей можно представить следующим соотношением:

t Пов.ок (т) = t n + A i cos ^L • ехр(-^ат) + 5.                                             (2)

Здесь t n - температура рабочего пространства в томильной зоне, при которой осуществляется выдержка металла; t n _oB . _OK - температура поверхности окалины; А_г - коэффициент, зависящий от температурного поля сляба в начале периода выдержки; L - расчетное сечение заготовки; а - коэффициент температуропроводности металла; ^ - первый корень уравнения ^ = ctg(^L), Л - коэффициент теплопроводности неокисленного металла, а - эквивалентный коэффициент теплоотдачи, 5 - перепад температуры по толщине окалины (считаем, что в течение процедуры измерений это практически постоянная величина [4]).

Примечание 2. Во-первых, в литературе, как это и отмечено выше, есть, как нам представляется, вполне достоверные сведения о том, что перепад температуры по толщине окалины в пределах томильной зоны можно считать примерно постоянной величиной. Во-вторых, промежуток времени между выдачами заготовок из методических печей стана «2500» ПАО «ММК» (Магнитогорский металлургический комбинат) в среднем составляет 2-4 мин. На такое относительно малое время и следует рассчитывать на реализацию процедуры определения производной температуры поверхности заготовки, из-за этого вполне обоснованно [25] можно считать, что перепад температуры в окалине является примерно константой. В-третьих, одним из вариантов объяснения этого утверждения могут быть следующие рассуждения. Как известно, плотность теплового потока через окалину q можно представить формулой q = Лок ^-, отсюда следует, что 8 = ^ок. В томильных зонах методических печей q уменьшается во времени, ок а толщина окалины ок, наоборот, растет, по этой причине произведение ∙ ок ≈ const, а следовательно, и 5 ~ const. Здесь Лок - коэффициент теплопроводности окалины.

При отсутствии окисления температура поверхности заготовки изменялась бы, следуя физике процесса, в соответствии с уравнением tПов.ме(т) = tn + A i cos ^L • ехр(-^ат).                                                   (3)

Из приведенных соотношений можно найти, что

^повокМ = ^^       ₁cosH₁L-exp(—H| ах).                              (4)

Таким образом, как это следует из (4), оценку производной температуры поверхности не-окисленного металла (что, собственно, и нужно для алгоритма контроля) можно заменить вычислением производной температуры поверхности окалины на слябе, что является весьма привлекательным обстоятельством при решении задачи контроля. Объясняется это прежде всего тем, что температуру поверхности окалины можно, хотя и не совсем просто, определить все-таки измерением на печи, а температуру поверхности неокисленного металла - практически нет. При этом к месту заметим, что практика использования производных температуры поверхности по времени в задачах определения нестационарного распределения температуры в слитках в литературе известна [26], здесь применялся, как это и само собой разумеется, метод регуляризации.

Как это видно из (4), их производные по времени равны, поэтому ставится задача определе- ния численных значений этих производных по результатам измерения температуры поверхности окалины tпэов.ок(τ) и числовому значению температуры рабочего пространства, при которой осуществляется выдержка tпэ. Из (4) также следует, что для этого по экспериментальным данным {tпов.ок(τ); tпэ} необходимо определить заранее неизвестные параметры ^1 и μ 1 . Решать эту зада- чу, как это обычно и принято, можно методом наименьших квадратов:

min 4,Hi (∑F=i{ln[t пэ(τ i)+ẟ-tпов.ок(τi)] - ln(-4i) - ln(cosμi^)+μlaτi}2).(5)

В данном случае перед составлением соотношения (5) применено такое линеаризующее пре- образование уравнения (2), как логарифмирование.

Решая задачу (5), получим, что

μ=  ∑”=1Tiln[∙] -1/n∙∑t=l^t∑ "=lln[∙] ;(6)

\    a/n∙(∑?=iTi)2-a∑i=iTi     ;(6)

41 = -ехр { ∑F=1 ln[∙] - lncosμ1^+μn∑ill τi)},(7)

где [∙] = [ t п ^э(τ i )+ẟ- t пов.ок (τ i )].

Из соотношений (4), (6) и (7) видно, что при использовании упомянутого подхода систематическая погрешность ẟ будет «вноситься» в оценки параметров ^1 и μ 1 , а следовательно, и в оцен- ки производных, что недопустимо.

Пример. Пусть в период выдержки металла в томильной зоне (120 ≤τ≤ 160 мин) для a=0,02м ; L = 0,0625 м; λ=29 Вт; α = 258,81 Вт ; tп = 1200 ℃; температура поверхно-ч                           м∙℃               м ∙℃   п сти неокисленного металла изменяется в соответствии с уравнением tпэов.ме(τ) = 1200+ + ^1 ∙cosμl-^ ∙ ехр(-μlaτ), где μ = 10,94 м 1, ^1 = -30 125 ℃. Если же будем считать, что перепад температуры в окалине составляет <5 = 10 ℃, то по формулам (6) и (7) получим, что μi = 11,73 м , 4i = -62 197 ℃; при ẟ = 20 ℃ уже будет μi = 12,79 м-1 , 4i = -186 407 ℃; а при ẟ=30 ℃ вычислим, что μ = 14,48 м 1, ^1 = -1 380 415 ℃. Таким образом, проявляется весьма заметное влияние систематической погрешности измерения на точность оценки парамет- ров μ и ^1 . В этом случае скорость изменения температуры поверхности во времени в период томления, вычисленная по формуле (4), будет следующей:

• 1)    при ẟ=0 ℃ - пэов.ок( -)=atпэов.ме( -) уменьшается от 465 до 94℃/ч;

• 2)    при ẟ = 10℃ atпэов.ок( -)=atпэов.ме( -) уменьшается от 522 до 83℃/ч;

• 3)    при ẟ =20℃ atпэов.ок( -)=atпэов.ме( -) уменьшается от 612 до 69℃/ч;

• 4)    при ẟ = 30℃ atпэов.ок( -)=atпэов.ме( -) уменьшается от 814 до 49℃/ч.

Вместе с тем коэффициент ^2 , вычисляемый в данном случае по формуле ^2 =   ∙ будет равен: 1) при ẟ =0 ℃ ^2 = 0,121 ч; 2) при ẟ= 10 ℃ ^2 = 0,125 ч; 3) при ẟ=20 ℃ ^2 = 0,133 ч; 4) при ẟ=30 ℃ ^2 = 0,147 ч.

Поэтому оценки перепада температуры по сечению заготовки при этом будут изменяться во времени (в процессе выдержки): 1) при ẟ=0 ℃ Δ t снижается от 56,3 до 11,3 ℃; 2) при ẟ= 10 ℃ Δ t снижается от 65,5 до 10,4 ℃; 3) при ẟ = 20 ℃ Δ t снижается от 81,3 до 9,1 ℃; 4) при ẟ = 30 ℃ Δ t снижается от 120,0 до 7,2 ℃.

Понятно, что случай, когда ẟ = 0 ℃ здесь считается эталонным и все погрешности должны определяться путем сравнения с данными этого режима. В связи с этим приведенные результаты позволяют заключить, что если для начала периода выдержки погрешность оценки перепада температуры по сечению сляба с помощью рассматриваемой процедуры вряд ли можно считать приемлемой, то к концу периода это далеко не всегда так и ошибка в расчете Δ t может быть и допустимой. Конечно, при этом следует иметь в виду, что в принципе метод, основанный на предварительной аппроксимации дифференцируемого сигнала (в данном случае температуры поверхности окалины) подходящей аппроксимирующей функцией, не пригоден для решения поставленной задачи, так как систематическая погрешность измерения температуры поверхности неокисленно-го металла обязательно «вносится» в параметры этой функции, а затем и в вычисляемую по ней производную и коэффициент ^2 , т. е. в оба сомножителя правой части уравнения Δt= .

Четырехточечный цифровой дифференциатор

Рассмотрим вариант решения поставленной задачи, основанный на непосредственном численном дифференцировании результатов измерений [27]. Существо рассматриваемого алгоритма заключается в следующем. Во-первых, средняя величина сигнала в ( i + 1)-й момент времени оценивается по четырем точкам, включающим текущее измерение и три предыдущих, т. е.

х = (X i +i + x_t + Xi _ i + Xi _ 2 )/4 .                                                                 (8)

Здесь x i = x(t i).

Во-вторых, найденное таким образом среднее значение X относится к середине отрезка времени, на котором располагаются данные точки (рис. 1).

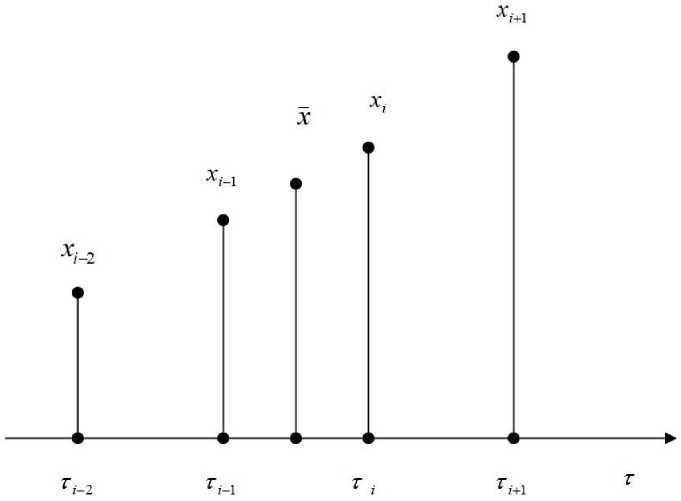
Рис. 1. Схема расположение точек, используемых при построении цифрового фильтра Fig. 1. Schematic diagram of the location of points used in constructing a digital filter

Очевидно, что в этом случае можно воспользоваться следующими четырьмя оценками про- изводной сигнала в ( i + 1)-й момент времени:

Лх(т ₁₊₁) _ х ₁₊₁ -х .

dт        1,5Дт ;

dx(т _^+1) _ Х [ -Х.

dт       0,5Дт ;

dx(T _i+1) _ x-x i-^

dx        0,5Дт ;

dX(T _i+i) _ X-X j-2

dx        1,5Дт .

Общеизвестно, что лучшей оценкой будет среднее арифметическое найденных частных оценок производной, т. е.

ГX  -x X -x x-x    x-x       122

dX(Ti+i) = Нгдг+^дт+п^ДЕ+ЛНДИ = д^Ь(Х+1-Х)+2(Х-Х2+2(Х-Хк22+з(^^ = dT                  44

= ^[Xi+1 + 3Xi-3Xi-i-Xi-2].(13)

одт

Из формулы (13) видно, что имеющаяся в каждом отсчете сигнала постоянная систематическая погрешность будет взаимно уничтожаться и не будет влиять на точность оценки его производной по времени. Кроме того, из-за усреднения как самих результатов измерений (используется среднее арифметическое отсчетов), так и оценок производных будет осуществляется фильтрация случайных помех, это общеизвестный и абсолютно проверенный результат и это показывает опыт применения авторами алгоритма (13) [27]. Далее, как это видно из формулы (13), алгоритм достаточно прост в вычислительном отношении, что, конечно, является его несомненным достоинством для применения в системах управления, работающих в режиме реального времени.

Вычислительное исследование алгоритма дифференцирования

На рис. 2 приведены использованная в вычислительном эксперименте эталонная кривая температуры поверхности неокисленного металла С П _ов . _ме(т) = 1200 + A_г • cos щ L • ехр(—р2ат), где Hi = 10,94 м^- \ A ! = -30 125 °C, и эта же кривая только с наложенными на нее систематической погрешностью б = 20 °C и случайной погрешностью из интервала [—5; +5] °C, полученной с помощью генератора случайных чисел с равномерным законом распределения. Последняя кривая имитирует реально измеренную температуру поверхности окалины (сляба) в период выдержки.

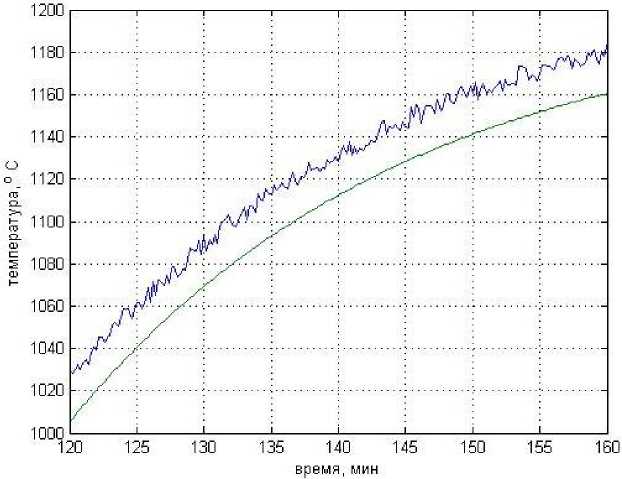
Рис. 2. Кривые изменения температуры поверхности неокисленного металла и поверхности окалины (сляба)

Fig. 2. Curves of change in temperature of the surface of unoxidized metal and the surface of scale (slab)

Вычислительные эксперименты показали, что в случае, когда в дифференцируемой кривой присутствует только постоянная систематическая погрешность, то алгоритм (13) дает, что и следовало ожидать, практически точное значение скорости роста температуры поверхности неокис-ленного металла (влияние 5 исключается). Относительная погрешность вычисления ^повме!-^ не превышала и 5 %.

Если же к эталонной кривой добавлялась еще и случайная погрешность, то при тех же условиях исследований все зависело от амплитуды этой случайной погрешности. Так, при увеличении этой амплитуды от 0 до 4 °C можно считать, что погрешность дифференцирования практически приемлема. Здесь средняя на всем промежутке времени (120≤τ≤ 160 мин) погрешность оценки перепада температуры по сечению сляба из-за цифрового дифференцирования изменялась от 2,8 до 10,2 °C.

Кроме того, погрешность дифференцирования, как и следовало ожидать, зависит и от размера шага по времени Дт. Так с увеличением этого шага от 1 до 2 мин погрешность выросла в среднем от 10 до 40 %. Также следует указать, что погрешность вычисления производной зависит и от момента времени, для которого она определяется. Объясняется это тем, что кривизна эталонной кривой уменьшается с течением времени, уменьшается вследствие этого и ^повме ¹¹ )

Для расширения диапазона применения алгоритма (13) по амплитуде наблюдаемых на практике помех использовали предварительную фильтрацию результатов измерений пэов.ок(τ), применялся следующий фильтр [27]:

эф пов.ок эф ^где ^ пов.ок

(О = Y t noB^k (0 + (1 — Y)i k ( j — 1),

- выходной сигнал фильтра; Y — некоторый коэффициент, выбираемый при настройке фильтра на конкретную статистическую ситуацию.

Алгоритм фильтрации найден из решения задачи оптимизации [27]. В работе [27] также показано, что данный алгоритм по структуре аналогичен алгоритмам фильтрации, построенным согласно известным подходам Р. Калмана.

На рис. 3 приведена идеальная кривая ^{пов.ме( )} , на этом же графике точками и крестиками для отдельных моментов времени указаны оценки этой производной, вычисленные по алгоритму (13) без и с предварительной фильтрацией данных по соотношению (14) соответственно. Здесь полагалось, что γ=0,2, а амплитуда помехи равна 4 ℃, т. е. помеха генерировалась в диапазоне [-4;+4] ℃.

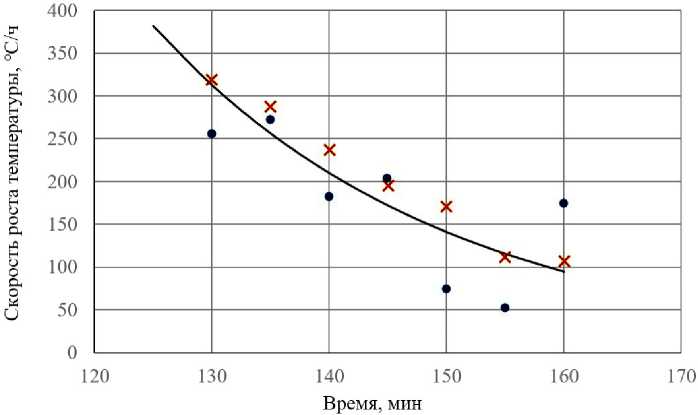
Рис. 3. Скорость роста температуры поверхности неокисленного металла Fig. 3. The rate of increase in surface temperature of unoxidized metal

Как видно из рис. 3, предварительная фильтрация существенно повышает точность оценки производной.

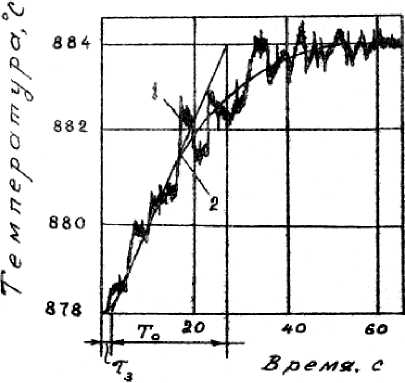
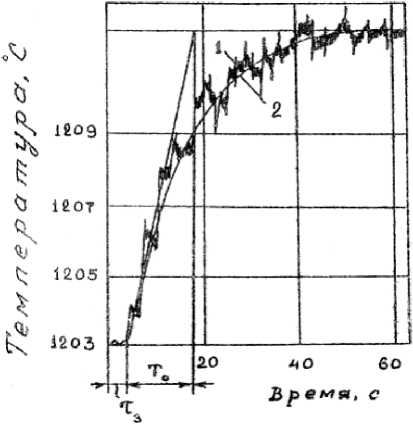
На рис. 4 приведены кривые разгона по температуре поверхности нагреваемых слябов в методической печи стана «2500» ПАО ММК, эти данные заимствованы из работы [28]. На рис. 4 7о итз – постоянная времени и время запаздывания объекта управления, показана графическая процедура определения этих параметров для первой (рис. 4а) и второй (рис. 4b) сварочных зон методической печи. Здесь же 1 – собственно экспериментальная кривая, 2 – ее аппроксимация.

a)

b)

Рис. 4. Экспериментальные кривые разгона по температуре поверхности нагреваемых заготовок [28] Fig. 4. Experimental curves of acceleration by surface temperature of heated workpieces [28]

Как видно из рис. 4, диапазон изменения реальных помех на печах не превышает и 1,5 °C, т. е. реальная помеха принадлежит диапазону [-0,75;+0,75] C. Выше было показано, что алгоритм дифференцирования (13) в таких условиях удовлетворительно сработает даже без предварительной фильтрации измеренных данных.

Выводы

Рассмотрено решение задачи контроля перепада температуры по сечению заготовок по скорости изменения температуры их поверхности в томильных зонах методических

печей. Отмечено, что использованиие такого подхода позволяет в принципе исключить влияние поверхностного слоя окалины на точность оценки контролируемого параметра. Исследованы варианты дифференцирования по времени температуры поверхности слябов в период выдержки при постоянной температуре рабочего пространства томильной зоны методических печей. Указаны условия их практической применимости. Результаты работы могут быть использованы при создании и совершенствовании алгоритмического обеспечения АСУ ТП нагревательных печей.