Контроль однопараметрического динамического объекта с памятью

В [1-2] рассмотрены алгоритмы контроля динамических объектов по одному и нескольким параметрам без учета изменения характеристик параметров процесса контроля во времени (памяти результатов контроля в предыдущие моменты времени). В ряде случаев при автоматическом контроле динамических объектов память необходимо учитывать, особенно тогда, когда интервал измерения параметра (при контроле по одному параметру) Т_к меньше интервала автокорреляции и процесса изменения значений параметра во времени.

Модель с конечной памятьюи постоянным интервалом Тк

Представим последовательность оценок значений параметра контролируемого объекта сообщениями , k – целочисленные моменты времени, моделью бесконечного эквидистантного ряда [3]

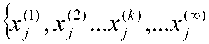
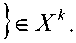
Каждый элемент ряда может содержать одно из N значений Такая последовательность может быть описана условной вероятностью вида

Последовательность является стационарной, если

P^/x^V^x^.x^^

= Р^х<к+Щ! хкк"’'пх''к+м"Т) х(к+м"п х<к+м"”^

для любого .

Собственное количество информации, содержащееся в оценке стационарной последовательности с памятью l -го порядка, определяется величиной

Величина среднего количества информации, содержащейся в одном сообщении, будет определяться энтропией ( l + 1)-го порядка

Н^Х^Н^Х'^М^х'^

-b-TP^--4+XW(x^x^f\x^ xX xp”

Справедливы следующие свойства меры (6). Если оценки являются статистически независимыми (отсутствует память), то

н№ = н<ху

Р(х^ Ix^x^V.X^Y

При возрастании порядка памяти функция (6) является невозрастающей функцией его памяти log N = Яо (X) >= Я, (X) >=...>= Н№ >=..., где N - имеет тот же смысл, что и в пояснениях к (1).

Отсюда следует, что элементы последовательности Х^к обладают информационной избыточностью вследствие наличия связи (памяти) или неравномерности распределения вероятностей оценок последовательности X^к.

Для определения количественной меры информационной избыточности применяется коэффициент избыточности [4]

ВД = 1-

НАХ) нот

_t нлх) . н_дху

[аде [0,1].

Величина R^X^ отлична от нуля, если:

• -    элементы последовательности Х^к обладают памятью ( l > 0);

• -    статистика оценок последовательности X¹ носит неравномерный характер - распределение разностей х^ отлично от равномерного распределения.

При автоматическом контроле динамических объектов по значениям оценок измеренных параметров объекта статистика оценок постоянна. Следовательно, коэффициент информационной избыточности R(X) зависит только от памяти последовательности Х^к , которая зависит от Т_к >  т_и .

В силу отмеченного в первом приближении за величину информационной избыточности оценки параметра в к момент времени, если известна оценка этого параметра в ( k - 1)-ый момент времени, предлагается принять значение нормированной функции автокорреляции R 1 ( т ) в момент времени к = т <  т ₀ , где т ₀ - интервал некоррелированности оценок контролируемого параметра в к -ый и в ( к - 1)-ый моменты времени.

Учет памяти первого порядка

Пусть в (к - 1)-ый момент времени известен относительный контрольный допуск [1] на параметр объекта контроля А^ . В момент времени к, отстоящий от (к - 1) на интервал времени тk < т0 , где т0 - интервал некоррелированности оценок контролируемого параметра в к-ый и в (к - 1)-ый моменты времени, выполняется контроль объекта по контрольным допускам [2]. При этом контрольный допуск должен рассчитывать- ся с учетом зависимости контрольного допуска в к-ый момент времени от контрольного, (7) можно записать

М(1)=Д^ + (А^_*^(г)), (8)

где АЛ(1) - величина относительного контрольного допуска в к -ый момент времени с учетом памяти l = 1; Хк - величина относительного контрольного допуска в к -ый момент времени без учета памяти, рассчитанная по методике [1]; А£-1 -величина известного в ( к - 1)-ый момент времени относительного контрольного допуска; RyA) - избыточность величины оценки контрольного допуска при получении ее в момент времени к < т = {( к - 1) - к }.

Учет памяти l-го порядка

Пусть в моменты времени к - 1; к - 2 .. к - l известны относительные контрольные допуски на параметр объекта контроля А£—1; А£—2;... /кк—1 . При этом также известно, что указанные контрольные допуски были рассчитаны по выражению (8) при известных значениях RДиз,RДтy..RAтУ Известно также, что интервалы времени т _k , к = 1; 2 ... l , определения оценок контролируемого параметра х^ е Х^к ,j = 1;2...7V разные и выполняется условие т l - т 1 <  т ₀ . В этих условиях при расчете контрольного допуска на параметр объекта контроля необходимо учитывать память l -го порядка и в формуле (8) значение А^ -1 необходимо рассчитывать с учетом следующих выражений

Хк_х = Ьк + (ДкД%(Д) ; (9) Хк_2 = Хк + (Ю)

xk_t=xk^5k_t_ARt^TA, (И)

где RA^,RA^-'-RA^ - избыточности величин оценок контрольных допусков в моменты времени к - 1, к - 2 . к - l .

Выводы

При автоматическом контроле динамических объектов необходимо учитывать память при определении контрольных допусков на параметры контролируемого объекта. Для модели процесса автоматического контроля с конечной памятью и постоянным интервалом Тк моментов измерения параметра объекта рассмотрена последовательность X оценок значений параметра контролируемого объекта сообщениями X j . При этом элементы последовательности обладают информационной избыточностью, которая оценивается коэффициентом избыточности R^ .

Для автоматического контроля динамических объектов в качестве меры оценки информационной избыточности при принятии решений о состоянии динамического объекта предложено значение нормированной функции автокорреляции R ₁ ( τ ) в момент времени k = τ <  τ ₀ , где τ ₀ – интервал некоррелированности оценок контролируемого параметра в k -ый и в ( k – 1)-ый моменты времени. Предложены формулы для расчета контрольных допусков на параметр с памятью 1 -го и l -го порядков.