Контурный анализ и современная оптика гауссовых пучков

Контурный анализ является одним из ключевых звеньев задачи распознавания изображений, суть которого заключается в исследовании изображения как набора контуров [1, 2]. В данной работе описывается новый способ распознавания контуров изображений, основанный на применении математического аппарата спиральных пучков – световых полей, сохраняющих свою структуру при фокусировке и распространении.

Сущность предлагаемого в работе подхода заключается в том, что все операции проводятся не с плоской кривой, задаваемой контуром, а с определяемым ею спиральным пучком. Это обусловлено тем, что выгоднее рассматривать обладающий рядом удобных свойств спиральный пучок (гарантированность его описания аналитическими равномерно-сходящимися функциями, большое количество способов его задания: амплитудой, корнями, коэффициентами разложения [3]).

Очевидно, что исход распознавания может (и должен) опираться на совокупность решений по многим выделенным на изображении контурам, и это легко достигается в том случае, когда существует механизм сравнения двух контуров. Именно нахождение качественных характеристик контура и извлечение из них информации о схожести является целью данной работы. Эта работа уточняет результаты, полученные в [4], а также обобщает подход распознавания на деформированные/зашумлённые контуры.

Отметим также, что область распознавания изображений разнообразна по применяемым методам и в последнее время ей уделяется значительное внимание как с теоретической, так и с практической точки зрения [5, 6].

1.    Описание контура

В задаче распознавания контурных изображений первой и обязательной процедурой является выделение границ (контуров) объекта. Но в данной работе подразумевается, что контуры уже были выделены одним из существующих способов. Следующим шагом является грамотное описание полученных контуров информацией, на основании которой будет непосредственно производиться процесс распознавания, а именно: её характеристики должны быть однозначны и инвариантны относительно различных факторов

(в частности, они не должны зависеть от выбора начальной точки). Забегая вперёд, отметим, что роль такой информации будут играть коэффициенты разложения спирального пучка. На рис. 1 приведено изображение корабля, на котором для простоты выделен единственный контур – его граница.

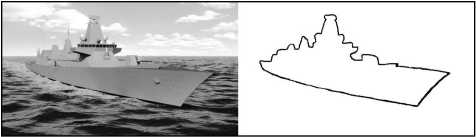
Рис. 1. Изображение (слева) и контур объекта (справа)

В данной работе математическим представлением контуров будем считать некоторые замкнутые плоские кривые, состоящие из упорядоченного набора точек:

Z ( t) = x ( t ) + iy(t ), t e [0, T ].

Очевидно, что любая замкнутая кривая представляет собой некоторую периодическую функцию с периодом T.

Конечно, каждый контур можно представить в виде бесконечного ряда по некоторой системе полных ортогональных функций. Задача разложения указанных функций детально освещена в [7], где приводятся классические базисы, применяемые в задачах распознавания изображений.

Проблема, однако, заключается в следующем. Конечный набор коэффициентов разложения по одномерному базису радикально зависит от того, с какой точки мы «начнём» кривую (задав её, таким образом, в интервале [0, T ] либо [ a , a + T ]). Конечно, с точки зрения кривой это не имеет никакого значения, но лишь при условии использования полного набора базисных функций, хотя на практике вычисления ведутся только с конечными суммами этих рядов. Следует отметить, что, если рассматривать кривую как двумерный объект, заданный на плоскости, эта проблема снимается. Однако платой за такой выбор является большое количество вычислений и асимптотический рост сложности таких алгоритмов. В данной работе рассматривается именно такой подход, в разделе 5 поясняется, как при этом бороться с указанными недостатками.

• 2.    Контур как исходный объект для формирования спирального пучка

Исследование световых полей различного типа выявило новый тип световых пучков, названных спиральными [3]. Оказалось, что спиральный пучок представляет собой световое поле, сохраняющее свою структуру интенсивности с точностью до масштаба и вращения при распространении и фокусировке. Кроме того, структура такого светового поля может быть весьма разнообразной, в частности, оно может иметь форму произвольной плоской кривой, в том числе замкнутой.

Установлено, что комплексная амплитуда S ( z , z ) такого пучка для порождающей кривой ζ( t ) имеет вид:

S ( z , z | ζ ( t ), t ∈ [0, T ]) =

[- zz ] T     J Z ( t ) Z ( t ) 2 zZ ( t )

= exP KH exP 1-    2 +     )^x        (²)

I P J 0     I P P J x exp |-1 j [?(<(т)-Z(<(Ti ] dr) | Z'( t) | dt,

IP 0                                 J где ρ – Гауссов параметр пучка, а черта означает комплексное сопряжение. Пример такой кривой и соответствующего ей спирального пучка приводится на рис. 2.

а)                     б)                   в)

Рис. 2. Порождающая кривая (а) и распределения интенсивности (б) и фазы (в) соответствующего спирального пучка

Важным является следующее свойство «квантования» спиральных пучков в виде замкнутых кривых. Если выполняется условие (квантования):

S curve = 12 πρ ² N q , N q = 0, 1 , 2 … ,                    (3)

где S_curve – площадь под кривой, то комплексная амплитуда пучка не зависит от начальной точки на кривой. Иными словами, спиральный пучок не определяется начальной точкой на контуре. Следовательно, любая конечная сумма ряда S_N ( z , z | ζ ( t ), t ∈ [ a , a + T ]) также не будет зависеть от этой начальной точки с точностью до общего унимодулярного члена, зависящего только от параметра a . Таким образом, снимается проблема начальной точки в анализе и распознавании входного контура. Это означает, что мы с любой требуемой степенью точности можем поставить в соответствие спиральному пучку S ( z , z | ζ ( t ), t ∈ [ a , a + T ]) его конечную сумму ряда:

_- zz _Nc

S „ ( z , z | Z ( t ), t e [ a , a + T ]) = e ^P £ ^ „ z " .           (4)

n = 0

Приведённое ниже выражение показывает, что при этом снимается ещё и проблема поворота анализируемого контура, поскольку при его повороте на угол α конечная сумма ряда изменяется следующим образом:

S N ( ze^{i α} , z e ^{- i α} | ζ ( t ), t ∈ [ a , a + T ]) =

_- zz _{N                    -} zz _N

= e P2 £(c„e")z" = e P2 £ c„z", n=0                       n=0

что лишний раз доказывает, что коэффициенты разложения способны характеризовать углы поворота.

Здесь следует отметить ещё один весьма важный аспект. Параметр квантования, как было показано в [8], определяет число нулей комплексной амплитуды внутри контура и, фактически, степень полинома, остающегося от исходной аналитической функции спирального пучка после взятия конечной суммы с требуемым количеством коэффициентов разложения. Очевидно, что если анализируемый контур сложен, то параметр квантования не может быть мал: нельзя сложное описать просто. Тем не менее, тот факт, что снимается проблема зависимости от выбора начальной точки и угла поворота, является весьма существенным и делает предлагаемый метод заслуживающим детального исследования.

• 3.    Контурный анализ

Пусть имеются два контура, входной и контрольный, находящийся в базе данных, и необходимо определить, соответствуют они друг другу или нет.

Перед построением пучков сделаем следующее: выберем шаги комплексных сеток, на которых будут вычисляться спиральные пучки так, чтобы площади, ограниченные кривыми, были равными. Приведение к одной площади позволяет снять проблему неизвестного масштаба изображения (он будет находиться через отношение шага одной сетки к шагу другой), сохраняя независимость от выбора начальной точки и угла поворота.

Построим для обоих контуров соответствующие спиральные пучки, оставляя необходимое количество членов [4]. По приведённой ранее схеме поставим контурам в соответствие два спиральных пучка, суть два набора комплексных коэффициентов: { c_n ⁽¹⁾} _n ^N ₌ ^c ₀ и { c_n ⁽²⁾ } _n ^N ₌ ^c ₀ . В том случае, когда параметр квантования достаточен, чтобы различить два контура, указанные наборы коэффициентов совпадают с точностью до вращения:

| c (1) |                          c (1) c (2)

n                           n n - 1

∀ n ∈ 1, N_c ,         = 1, ϕ _n = ln .             (6)

| c_n (2) |                  i c_n (2) c_n (1 _- )₁

Если ϕ _n ≡ const для всех n , то ϕ _n – угол взаимного поворота контуров α . Этот факт легко получить, записывая соотношение двух комплексных амплитуд из представления спирального пучка в виде сумм (4).

Если же условие (6) не выполняется, можно констатировать несоответствие контуров друг другу.

• 4.    Алгоритм контурного анализа

2. Построение 3. Разложение по базису

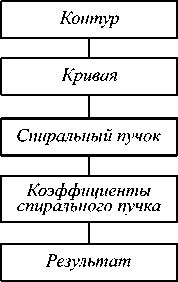
На основе вышесказанного можно кратко сформулировать пошаговую последовательность действий (блок-схема, рис. 3.) по определению схожести двух предложенных контуров. Во-первых, их необходимо задать в виде упорядоченного набора точек плоскости – кривой (шаг 1). По полученным кривым следует вычислить соответствующие им спиральные пучки (шаг 2) и разложить по ортогональной системе (шаг 3), взяв требуемое количество коэффициентов разложения, которое эмпирически определяется рамками задачи. И наконец, на основании сравнения двух наборов коэффициентов можно сделать вывод о том, являются ли два контура одинаковыми с точностью до масштаба и вращения (шаг 4).

1. Описание

J 4. Обработка

Рис. 3. Блок-схема алгоритма распознавания

Таким образом, реализуется алгоритм распознавания, обладающий следующими особенностями.

Во-первых, это независимость работы алгоритма от выбора начальной точки на контуре и масштаба контурного изображения. Во-вторых, контурный объект может быть произвольной формы; его сложность определяется только разрешением системы, а не количеством звеньев контура, характерным для других методов. В-третьих, все проводимые компьютерные вычисления на шагах 1 –3 непосредственно используются при принятии решения, на них нет переборных операций-подсчётов, которые отбрасываются. Так, последние две особенности выглядят достаточно привлекательными на фоне такого общепризнанного метода распознавания контуров, как анализ с использованием корреляционных функций (см. [2]).

Далее отметим, что при первоначальном рассмотрении метода шаги 2 и 3 выглядят очень ресурсоёмкими, поскольку оперируют двумерными объектами: комплексными амплитудами на плоскости и базисами. Однако авторами был найден и проверен способ уменьшить количество вычислений на 2–3 десятичных порядка, сведя реальные подсчёты к одномерным. Фактически шаги 2 и 3 объединяются в один по прямому вычислению коэффициентов разложения с использованием лишь одномерных интегралов. К сожалению, такие важные в прикладном значении подробности выходят за рамки данной статьи, предполагающей изложение общей концепции распознавания контуров при помощи спиральных пучков света.

К недостаткам данного подхода можно отнести следующее. Во-первых, при вычислениях используется операция экспоненцирования, которая является весьма «тяжёлой» для подсчёта, особенно на мобильных устройствах. Во-вторых, на текущий момент не известны эффективные оценки на параметр квантова- ния и количество членов остаточного ряда, достаточных (и необходимых) для устойчивости результатов распознавания. Этот вопрос ещё недостаточно проработан и требует дальнейшего исследования.

5.    Учёт шумов

Итак, основная канва метода сформулирована и описана в виде последовательности шагов, однако при переходе от рассмотренных ранее теоретических выкладок к практической реализации подхода необходимо сделать некоторые дополнительные замечания. Следует отметить, что в реальных системах неизбежно присутствуют факторы, которые в данной статье пока не были учтены: шумы и искажения. Причин их наличия много: ошибки дискретизации в ПЗС-матрицах, сбои при передаче информации с устройств регистрации изображения на вычислительную технику, реализующую процесс распознавания, и прочее.

Авторами было проведено исследование того, как предлагаемый подход реагирует на искажения подобного рода. Метод оказался весьма устойчивым к наличию шумов в распознаваемом контуре. Прежде всего, это связано с тем, что в выражение для комплексной амплитуды спирального пучка (2) входит Гауссова экспонента, которая оказывает «сглаживающий» эффект, проявляющийся в том, что небольшие деформации контура приводят лишь к соответствующим изменениям комплексной амплитуды.

Несмотря на то, что комплексная амплитуда и её нули устойчивы к деформации контура, коэффициенты разложения (см. формулы Виета, например, в [9]) могут варьироваться, притом весьма значительно. Это не мешает продолжать их использовать для распознавания, поскольку усечённые ряды (4) сходятся равномерно и весьма «быстро», основные информационно-значимые коэффициенты имеют номера меньше параметра квантования.

Кроме того, есть возможность воспользоваться дополнительной, слегка модифицированной глобальной характеристикой (в отличие от «локальных» коэффициентов), которая в оптике световых полей известна как «коэффициент перекрытия», а в функциональном анализе – как нормированное скалярное произведение в гильбертовом пространстве L2 (ℝ2) . Фактически K(θ) представляет собой корреляционную функцию по углу взаимного поворота θ спиральных пучков S(1) (z,z) и S(2) (z, z) , где мерой близости выступает скалярное произведение из числителя формулы (7). Максимум модуля этой функции достигается при истинном угле взаимного поворота α распознаваемых контуров.

K ( θ ) =                         ×

∫∫ S ⁽¹⁾( z , z ) S ⁽¹⁾( z , z ) d x d y

∫∫ S ⁽¹⁾( z , z ) S ⁽²⁾( ze^{i θ} , ze ^{- i θ} ) d x d y

∫∫ S ⁽²⁾( z , z ) S ⁽²⁾( z , z ) d x d y

В отличие от метода распознавания посредством корреляционных функций, описанного, например, в [2], выражение (7) обладает следующими достоинствами: количество слагаемых в каждой сумме – это количество коэффициентов разложения (порядка десятков, одной – двух сотен штук), а не звеньев, задающих контур (более 500). Кроме этого возможно нахождение угла поворота с требуемой точностью: если шаг изменения угла θ для нахождения максимума функции корреляции мал – достигается большая точность, если велик – большая скорость.

При помощи формулы (4) и свойства ортогональности базиса Лагерра – Гаусса выражение (7) может быть с лёгкостью переписано в представлении с использованием только коэффициентов разложения:

N

Ус (1)с(2)е inа nn

K ( 9 ) = ,     n =0      г- .                         (8)

NN

• (1)    (1)            (2) (2)

6.    Низкая детализация как экспресс-тест для сравнения 7.    Численное моделирование

∑ c_n c_n ∑ c_n c_n

V n=0            ч n=0

Таким образом, появляется новый инструмент, который может уточнить и подтвердить при необходимости результаты распознавания, рассчитанные исключительно при помощи коэффициентов.

Факт неустойчивости коэффициентов разложения побудил к поиску дополнительных решений, позволяющих нивелировать влияние шумов на рассматриваемый метод. Это привело к рассмотрению уже упомянутых корреляций, а также ситуации, названной нами «случаем сверхмалой детализации».

Идея заключается в следующем: если в случае большого количества коэффициентов разложения их точность может ухудшаться с наличием шумов, то следует строить спиральные пучки с очень маленьким параметром квантования (от 2 до 5). При этом интенсивность такого светового поля уже не будет внешне напоминать порождающую кривую, как это было на рис. 2, однако с точки зрения применения теоремы Виета и энергетических характеристик получающегося светового поля такой подход оправдан.

Как будет видно из раздела с численным моделированием, такое решение даёт неожиданно хорошие результаты, хотя неочевидно, что, если ограничиться лишь двумя-пятью коэффициентами разложения, не потеряется значительная доля информации о порождающей кривой. При этом скорость получения результата возрастает многократно. Это позволяет рассматривать случай сверхмалой детализации как своеобразный экспресс-тест на масштаб и потенциальный угол поворота, сохраняя все достоинства и нивелируя часть недостатков оригинального метода, кратко изложенного в 5-м разделе данной статьи. Повторимся, случай сверхмалой детализации не является основой для принятия решения о схожести объектов, он призван отфильтровать большое количество сильно различающихся контуров и выдать гипотетический угол поворота, который может быть проверен корреляционной функцией (7) высокодетализированных спиральных пучков (в этом случае нахождение максимума корреляции существенно упрощается – поиск взаимного угла поворота следует производить в окрестности гипотетического угла).

В качестве тестового образца было выбрано изображение самолёта, вручную выделен контур границы, и построен для него спиральный пучок. После этого в графическом редакторе контур был повёрнут на 123 градуса, уменьшен до 75 % от исходного, и построен соответствующий ему спиральный пучок.

Рис. 4. Слева направо: исходное изображение самолёта, выделенный контур границы, интенсивность порождённого спирального пучка

С целью наглядной визуализации при построении, параметр квантования N q был выбран равным 30, количество коэффициентов разложения N c – 120. Значение Гауссова параметра ρ = 1, площади под кривой S curve = 15π. Функция корреляции при этом достигает максимума своего абсолютного значения 0,8 при искомом угле 123 градуса и масштабном множителе 1,3. По определению K (θ), максимум её модуля не превосходит 1, иными словами, констатируется схожесть верхнего и нижнего контуров, но не абсолютная, что является следствием обработки (на рис. 4 заметны пропадания звеньев самолёта в районе «хвоста»).

Перейдём к случаю сверхмалой детализации (рис. 5). Для этого параметр квантования N q и количество коэффициентов N c были выбраны равными 3.

Рис. 5. Слева направо: исходное изображение самолёта, выделенный контур границы, интенсивность порождённого спирального пучка

Значение Гауссова параметра ρ = 1, площади под кривой S_curve = 1,5π. Функция корреляции при этом достигает максимума своего абсолютного значения 0,998 при угле 121 градус и масштабном множителе 1,3. Коэффициенты разложения, вычисленные для критерия (5), представлены в табл. 1.

Табл. 1. Коэффициенты разложения и применение критерия

n	(1) n	(2) n	| cn (1) | | cn (2) |	ϕ n
1	–0,088–0,335i	–0,286+0,175i	1,034	–98
2	–0,482+0,517i	–0,577 +0,155i	1,182	–139
3	1,175–2,049i	–0,365 +2,131i	1,093	–128
Среднее значение угла поворота				–122

Следует отметить, что сами по себе углы потенциального поворота φ _n не вполне удовлетворяют критерию, однако обнаружена специфическая особенность: их среднее арифметическое значение даёт искомый угол поворота с небольшой погрешностью. Этот факт привлекает наше внимание, поскольку он подтверждён многочисленными численными экспериментами, но ещё не был детально проанализирован.

Таким образом, численные эксперименты показывают, что представленный на рис. 3 алгоритм может успешно применяться и в ситуации, когда распознаваемый контур зашумлён или деформирован. В этом могут помочь дополнительные инструменты: корреляция K (θ) и случай сверхмалой детализации.

Заключение

В данной работе предлагается к рассмотрению новый подход в рамках контурного анализа, основанный на тесном взаимодействии когерентной оптики, теории функций и численных методов. Показан и теоретически обоснован алгоритм сопоставления контуров, позволяющий определить, являются ли два контура одинаковыми с точностью до масштаба и/или вращения. Продемонстрирована динамика развития предлагаемого подхода в случае присутствия шумов или деформаций на исследуемом изображении. Отмечен факт уменьшения количества производимых вычислений на ЭВМ путём сведения задачи к подсчёту одномерных интегралов. Введены в рассмотрение дополнительные инструменты, которые позволяют уточнить результаты распознавания: корреляция и сверхмалая детализация.

Предполагается продолжение исследований в следующих направлениях: во-первых, проведение анализа производительности по сравнению с классическими методами контурного анализа; во-вторых, получение асимптотических оценок на алгоритмическую сложность предлагаемых вычислений; в-третьих, выработка критериев оценки получаемых значений корреляции.

Работа выполнена при поддержке Министерства образования и науки РФ.