Конвертирование вихревых пучков оптического диапазона в радиодиапазон на основе нелинейной генерации разностной частоты

В последние десятилетия в области телекоммуникаций наблюдается повышенный интерес к использованию вихревых пучков – электромагнитных волн, обладающих орбитальным угловым моментом. Это связано с тем, что различные квантованные состояния проекции орбитального углового момента на направление распространения могут быть использованы как для кодирования сигналов, так и для мультиплексирования каналов связи. Таким образом, вихревые пучки открывают дополнительные возможности как для увеличения скорости передачи информации, так и для повышения помехоустойчивости и защищенности каналов связи. Одним из приоритетных направлений развития инфокоммуникаций является радиофотоника – гибридные системы, совмещающие процессы преобразования сигналов в радио- и оптическом диапазоне. В настоящее время в радиофотонике осваивается микроволновый диапазон, лежащий в терагерцовой области частот 0,1 –50 ТГц, как наиболее перспективный с точки зрения малой загруженности электромагнитного спектра.

Перспективным направлением радиофотоники в области телекоммуникаций является разработка систем Radio-over-fiber (RoF) [1], в которых используется передача радиосигналов микроволнового диапазона по оптическому волокну. В контексте развития систем RoF возникает проблема преобразования сигналов, переносящих орбитальный угловой момент в оптическом диапазоне, в сигналы, переносящие таковой в радиодиапазоне. В данной работе рассматривается процесс преобразования вихревых пучков оптического диапазона в области длин волн λ≈ 1,5 мкм в вихревые пучки радиодиапазона в области частот, превышающих 100 ГГц.

Нелинейные среды с отличной от нуля поляризуемостью (диэлектрической восприимчивостью) второго порядка широко используются для конвертирования электромагнитных волн оптического диапазона в радиоволны терагерцового диапазона на основе генерации разностной частоты. При этом нелинейная среда, являющаяся источником генерации, модифицируется дополнительными включениями (легируется) или структурно изменяется с целью повышения конверсионной эффективности. Так, в работе [2] используется решетка фотонных кристаллов. В статье [3] генерация происходит в полосковом металлическом волноводе с включением примесей GaAs. В работе [4] используется прямоугольный металлический волновод, заполняемый периодически чередующимися слоями LiTaO3 с противоположной ориентацией оптических осей. В [5] генерация разностной частоты осуществляется в 2D плазмонном волноводе, состоящем из слоя LiNbO3 и располагаемом между двумя плоскими неметаллическими слоями. В работе [6] описана генерация разностной частоты в Гауссовых пучках, а также приведены результаты экспериментальной генерации разностной частоты в кристалле LiNbO3, содержащем планарные волноводы.

Что касается исследований по преобразованию вихревых пучков в нелинейных средах с поляризуемостью второго порядка, можно отметить следующее. В работе [7] показано, что при генерировании второй гармоники происходит удвоение топологического заряда вихревого пучка m , который является целым квантовым числом и определяет проекцию орбитального углового момента на направление распространения, обусловленную зависимостью электромагнитного поля вихревого пучка от азимутального угла φ в виде e^{im φ}.

В работе [8] высказывается гипотеза и приводится косвенное теоретическое обоснование и результаты компьютерного моделирования, подтверждающие факт равенства топологического заряда выходного вихревого пучка сумме зарядов входных вихревых пучков при генерировании суммарной гармоники. В работе [9] теоретически и экспериментально исследуются законы сохранения топологического заряда при генерации второй гармоники, включая состояние с дробным топологическим зарядом. В работах [10, 11] экспериментально подтверждается закон сохранения топологического заряда при генерации второй гармоники [10], суммарной гармоники [11], где также дано теоретическое обоснование полученных результатов. В работе [12] экспериментально установлено, что в многослойной нелинейной среде с периодически чередующимися слоями LiTaO3 с противоположно направленными оптическими осями для обеспечения пространственного фазового синхронизма при генерации суммарной гармоники топологические заряды суммируются.

В работе [13] на основе вычислительных экспериментов и теоретически исследуется влияние длины нелинейной среды на процесс параметрического усиления света в процессе смешения Лагерр–Гауссовых мод, устанавливается закон сохранения топологического заряда, а также исследуется влияние радиальных индексов Лагерр–Гауссовых мод на процесс параметрического усиления.

Анализ работ в области конвертирования оптического излучения в радиодиапазон на основе использования нелинейных сред с восприимчивостью второго порядка показывает, что в основе теоретического обоснования и моделирования происходящих процессов генерации лежит система из трех уравнений, описывающих процессы в приближении слабо меняющихся амплитуд [14] вне зависимости от структурной организации нелинейной среды.

Несмотря на генетическое родство различных процессов трёхволнового смешения – генерация второй гармоники, суммарной частоты, параметрическое усиление, генерация разностной частоты – каждый из перечисленных процессов имеет свои особенности, в частности, отличительной чертой процесса генерации разностной частоты в радиодиапазоне является очень низкая энергетическая эффективность конверсии, обусловленная двумя факторами: 1) малостью отношения нелинейной части поляризации к линейной, что характерно для всех трёхволновых процессов, исключая область экстремально высоких значений напряженности электрического поля исходных гармоник; 2) в силу дипольного механизма излучения волн в кристалле мощность дипольного излучения пропорциональна квадрату частоты, следовательно, в исследуемом диапазоне частот соотношение мощностей излучения в радио- и оптическом диапазоне является малой величиной, пропорциональной квадрату отношения соответствующих частот, и составляет в контексте данной работы величину ~10–5–10–6.

Целью данной работы является исследование процесса конвертирования излучения оптического диапазона в радиодиапазон в условиях, оговоренных выше.

1. Моделирование процесса конвертирования

вихревого пучка

Распространение электромагнитной волны линейной среде описывается уравнением [15]:

—                               —

V2E— - A d2E = 1 d2Pnl c2 812    c2e0 dt2 , где E – вектор напряженности электрического

—*

——

в не-

поля,

с – скорость света в вакууме, ε – диэлектрическая проницаемость среды, P_NL ( x , y , z , t ) – вектор нелинейной поляризации.

Представим решение уравнения (1) в виде:

——

——

E ( x , y , z , t ) = A ( z )Y( x , y , z )exp( ikz - i ю t ), где k = (го/ c )Ve, a A ( z ) и T ( x , y , z ) - некоторые плекснозначные функции.

Представим оператор Лапласа в форме:

• V ² =V ² + — ,

• ¹    d z²

где

V^ + ^_ .

d x ² d y ²

Используя представление (2), найдем:

a ² e =U2 ; a _{y + 2} d z ² I d z²

——                 ——

d A d Y „a A„, ., ^— d ² Y --+ 2—Y ■ ik + A ---+

8 z 8 z     8 z

d z¹

и

ком-

^— d Y    -„.

+ 2 A — ik - A Y k ² exp( ikz - i ю t ). d z            J

—

Будем считать, что в выражении (2) функции A ( z )

Y ( x , y , z ) являются медленно изменяющимися по

сравнению с e ^ikz функциями координаты z . Тогда в параксиальном приближении справедливо неравенство:

—

—

8 ² A , 8A --^ k —, d z ² d z

8 ² Y , dY --« k — .

.

8 z ²       8 z

С учетом соотношений (5) выражение (4) представляется в виде:

82E

" i z²

——

d A d Y

—

a r

—

—                           —

2-- + ikY + 2 A--ik - A Yk ²

d z d z

d z

x

x exp( ikz - i ю t ).

Учитывая, что в представлении (2) функция Ψ не определена, подчиним ее параболическому уравнению:

dY

V ² Y + 2 ik — = 0.

¹         d z

Если электрическое поле представляет некоторую суперпозицию волн c частотами ω i , волновыми чис-

лами k i и направлениями поляризации е i , то напряженность электрического поля и поляризацию можно представить в форме:

R ( z ) = z

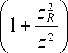
E — ^ e_iA_i(z )¥ i ( x , y , z )exp( ik i z - i ю it ), P nl — ^ S i P ( z )exp( k i z - it^t ).

Тогда из уравнения (1) с учетом соотношений (2), (6), (7) и (8) следует:

d A i d z

84*

— + ik , Y , dz

e k z

ω ² 2 c ² ε ₀

P .

Рассмотрим процесс генерации вихревого пучка на разностной частоте:

Ю 3 = Ю 1 - Ю 2 ,

где ω 1 и ω 2 – частоты оптического диапазона, ω 3 – частота радиодиапазона.

Пусть нелинейная среда описывается нелинейностью второго порядка: *                                      *

P nl — 8 o X ⁽²⁾ E ■ E ,                                  (11)

где x ⁽²⁾ - диэлектрическая восприимчивость, в общем случае представляющая собой тензор 3-го ранга

X ⁽²⁾ = X ( jk ’, E ■ E = E j E k .

Для упрощения будем считать среду изотропной. В этом случае поляризацию можно представить в скалярном виде:

P nl — d ■ E².                                       (12)

В случае анизотропной среды поляризацию также можно представить в скалярной форме (12), если ввести понятие эффективной восприимчивости d eff [18]. В этом случае тензорный характер восприимчивости учитывается при расчете d eff .

Пусть в нелинейной среде в направлении оси z распространяются два лазерных одномодовых параксиальных пучка на частотах ω 1 и ω 2 , переносящих угловые моменты, азимутальные индексы которых соответственно m 1 и m 2 .

Параксиальные пучки с азимутальными индексами m j удовлетворяют параболическому уравнению (7) и в общем виде представляются распределениями вида:

T j (p, Ф, z ) = Ф(р, z , m )exp( im_Jф),                (13)

где j =1,2, p = x ²+ y ², ф = arctg( y / x ).

Комплексная амплитуда лазерных пучков может иметь различную форму [16– 18], в частности, семейство пучков Лагерра–Гаусса описывается распределением:

Ф LG (р, z , m , n ) = -^°- exp σ( z )

k ρ ² ρ ²

■ i ---1

2 R ( z ) σ ² ( z )

где

радиус кривизны параболического фронта пучка,

g( z ) = G o

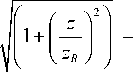
радиус пучка, σ 0 – радиус перетяжки пучка, z_R — па 0 /X - конфокальный параметр Рэлея, L m -присоединенный полином Лагерра.

Поскольку влияние радиального параметра семейства Лагерр–Гауссовых пучков n в данной работе не рассматривается, класс распределений можно сузить, положив n =0.

Генерирование разностной гармоники – это процесс трехволнового смешения. В результате перехода к скалярному представлению, электрическое поле в среде можно записать в виде суммы трех волн, описывающих распространение вихревых пучков с проекциями углового момента m 1 , m 2 и m 3 на частотах ω 1 , ω 2 и ω 3 :

E — A 1 ( z )Ф 1 ( x , y , z ) exp( ik 1 z - i Ю 1 1 + im ₁ ф) +

+ A ₂ ( z )Ф ₂ ( x , y , z ) exp( ik ₂ z - i ю ₂ 1 + im ₂ ф) + (15)

+ A 3 ( z )Ф ₃ ( x , y , z ) exp( ik 3 z - i ю ₃ 1 + im ₃ ф) + к.с.,

где

ω 1 ω 2 ω 3

k1 —---V^ , k2 —---V^2 , kз —---"у^З ; ^1, ^2 и 83 — ccc

значения диэлектрических проницаемостей на частотах ω 1 , ω 2 и ω 3 соответственно; Ф j – распределения семейства (14), соответствующие азимутальным индексам m j .

Скалярную нелинейную поляризацию запишем в виде:

P NL — ^ P j exp( ik j z - i ю j t + im j ф) + к.с.,         (16)

j — 1

что соответствует второму уравнению (8) в скалярном представлении для вихревых полей. Для нелинейной среды, представляемой в виде (12), получим:

P_NL — d [ A ₂ A ₃ Ф ₂ Ф ₃ exp( - i Ю 1 1 + i ( k ₃ + k ₂ ) z ) + + i ( m ₂ + m ₃ )ф) + A 1 A ₃* Ф ₁ Ф * exp( - i ю ₂ 1 + + i ( k 1 - k ₃ ) z + i ( m 1 - m ₃ )ф) + A 1 A 2 Ф 1 Ф 2 x x exp( - i ю ₃ 1 + i ( k 1 - k ₂ ) z + i ( m 1 - m ₂ )ф) + к.с. ] .

В выражении (17) при возведении в квадрат мы оставили только члены, соответствующие процессу генерации разностной частоты, т.е. члены, удовлетворяющие соотношению (10). Таким образом, в выражении (17) следует считать

f ^р 1' L °( z ) J

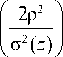
x exp

ю 1 — ю ₃ + ю ₂ ,

z i (2 n + m + 1) arctg— , zr _

Ю 2 — Ю 1 - Ю 3 ,

Ю 3 — Ю 1 - Ю 2 .

Сопоставляя выражения (16) и (17), найдем:

P 1 = dA₂ А 3 Ф 2 Ф 3 exp( - i m, t + i ( k₃ + k ₂ ) z + i ( m ₂ + m 3 )ф),

P₂ = d/! _l A * Ф _l Ф * exp( - im₂1 + i ( k1 - k ₃ ) z + i ( m i - т ₃ )ф), (19)

P₃ = dA₁A * Ф₁ Ф* ₂ exp( - i m 3 1 + i ( k , - k ₂ ) z + i ( m , - т ₂ )ф).

В выражениях (22) функции F j ( z , m j ) и B j ( p , z , m j ) определяются соотношениями:

Используя уравнение (9) для каждой из распространяющихся волн, приходим к системе уравнений:

B j = di^ - ik j Ф j , dz

dA dz

— + ik Ф, dz ^{1 1}

х exp( i A mф);

m 2

= d — A ₂ A ₃ Ф ₂ Ф ₃ exp( i A kz ) х c ²

да d ф ,- F j⁽ z , m j ) =

₀ dz

, (d

+ikj I Ф jФ

I

. *

d Ф *

■     2 + dz

A                         (24)

d Ф. 1

+ k ² Ф * Ф_у)2np d p.

dz I

dA₂ Г d Ф₂ ., -I , m2                       x

--- —2 + ik2 Ф2 = d — AA*Ф1Ф3exp(-i A kz) х dz L dz J    c2                          (20)

х exp( - i A m ф);

dA 3 d Ф 3      .

+ ik ₃ Ф ₃ dz dz

dz

m 2

= d — A 1 A ₂ Ф ₁ Ф ₂ exp( - i A kz ) х c ²

х exp(-iAm ф), где Am = m 1- m2-m3, Ak=k3 + k2-k 1.

Анализируя систему уравнений (20), видим, что левые части каждого уравнения не зависят от угла ф, таким образом, решения системы (20) существуют при выполнении условия A m = 0, следовательно, в квадратичной нелинейной среде из исходных вихревых пучков, переносящих угловые моменты с азимутальными индексами m 1 и m ₂ на частотах m 1 и m₂, генерируется вихревой пучок разностной частоты to ₃ = to , - to ₂, переносящий угловой момент с проекцией на направление распространения, равной разности проекций m 3 = m 1 - m 2 .

Следуя приему, изложенному в работе [5], умножим каждое j -е уравнение системы (20) на комплексно сопряженный множитель

(dФ*/ dz) - ikjФ*j и проинтегрируем уравнения по поперечному сечению соответствующих пучков. Окончательно для определения амплитуд А, получим систему:

dA , m 2

— = - d — A 2 A 3 exp( i A kz ) I 1 ;

dz2 dA2 = - d    A, A*exp(-iA kz) 12;(21)

dz2

dA3, m

— = -d — AA2 exp(-1Akz)13, dz2

где введены обозначения:

да j Ф2 (p, z, m 2 )Ф3 (p, z, m 3) B1 (p, z, m )2np dp

11 =

F 1 ( z , m 1 )

да j Ф1 (p, z, mx )Ф3 (p, z, m 3) B2 (p, z, m 2 )2np dp

F 2 ( z , m 2 )

;

да j Ф1(p, z, m1)Ф2(p, z, m 2) B3 (p, z, m 3 )2np dp

1 3 = -------------------------------------------

F , ( z , m 3 )

2. Имитационное моделирование процесса конвертирования вихревых пучков

Имитационное моделирование процесса конвертирования вихревых пучков оптического диапазона в радиодиапазон осуществляется с помощью численного решения уравнений (21) в пакете математического моделирования Matlab с помощью метода Рунге-Кутта. Процесс генерации разностной частоты исследовался в диапазоне частот 100-700 ГГц. Оптическое излучение соответствовало длинам волн С-диапазона. Мощность лазеров накачки составляла Р 1 = Р 2 = 1 Вт. Эффективная нелинейная восприимчивость нелинейной среды, в которой происходит процесс конвертирования, выбрана равной d eff =1,5Л0^-12, показатели преломления на оптических частотах равны n 1 = n 2 = 2,2, на радиочастотах n ₃ = 2,5.

Для генерации радиовихревых пучков с топологическим зарядом m ₃ = 1 использовались Лагерр-Гауссовые лазерные моды с радиальными индексами n 1 = n 2 = 0 и азимутальными индексами m 1 = 1, m 2 = 0. Моделируемая система изображена на рис. 1.

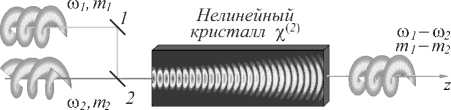
Оптические                        Вихревой вихревые пучки                      радио пучок

Рис. 1. Моделируемая схема конвертирования вихревых пучков: 1 - непрозрачное зеркало, 2 - полупрозрачное зеркало

С точки зрения технического приложения результатов представляет интерес исследование характера изменения модуля амплитуды получаемого радио-вихревого пучка, подчиняющейся соотношению (21), при изменении длины нелинейного кристалла, что и представлено на рис. 2. Расчет проведен для радио-вихревого пучка с топологическим зарядом m 3 = 1 в зависимости от протяженности нелинейной среды для различных значений радиусов перетяжки лазерных пучков накачки. Из полученных данных следует, что при малых длинах нелинейной среды наблюдается линейная зависимость амплитуды от длины. При увеличении длины нелинейного кристалла амплитуды вихревых радиопучков выходят на соответствующие асимптотические значения.

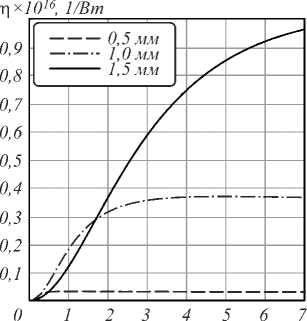
На рис. 3 показана зависимость показателя эффективности генерации п вихревого радиопучка от длины кристалла. Показатель эффективности в соответ- ствии с работой [6] определяется соотношением, имеющим размерность 1 / Вт:

η =

P 3

P 1 ⋅ P 2 ^,

где Р 1 и Р 2 – мощности лазеров оптической накачки, Р 3 – мощность вихревого радиопучка. Выбор данного соотношения обуславливается тем, что в приближении «неистощаемости» амплитуд исходных оптических пучков А 1 = const и А 2 = const амплитуда разностной частоты А 3 определяется произведением амплитуд А 1 и А 2 в соответствии с последней формулой выражения (21). Таким образом, показатель η оказывается независимым от амплитуд исходных оптических пучков. Расчеты показывают, что зависимости амплитуды А 3 разностной частоты и показателя эффективности η от длины кристалла при различных значениях радиуса перетяжки сигма имеют схожий асимптотический характер.

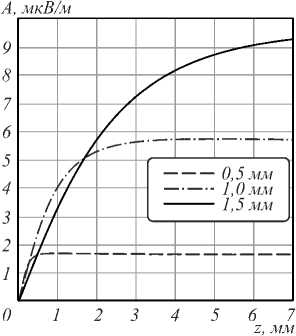
Рис. 2. Зависимость модуля амплитуды вихревого радиопучка A от протяженности нелинейной среды z при трех значениях радиуса перетяжки лазерных пучков

Z, Л1Л1

Рис. 3. Зависимость показателя эффективности генерации η вихревого радиопучка от протяженности нелинейной среды z при трех значениях радиуса перетяжки лазерных пучков

На рис. 4 изображена зависимость показателя эффективности генерации радиовихревого пучка от разности частот между лазерами накачки. С ростом разности частот величина η заметно возрастает, что обусловливается дипольным механизмом излучения, как было отмечено выше.

На рис. 5 показана зависимость показателя эффективности от радиуса перетяжки лазерных пучков. Данная зависимость носит экстремальный характер, т.е. для заданных мощностей накачки существует значение радиуса перетяжки луча, при котором наблюдается максимум эффективности конвертирования излучения.

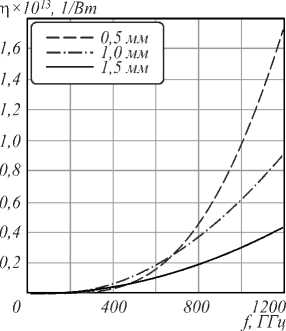
Рис. 4. Зависимость показателя эффективности генерации η вихревого радиопучка от разностной частоты лазерных пучков при трех значениях радиуса перетяжки лазерных пучков

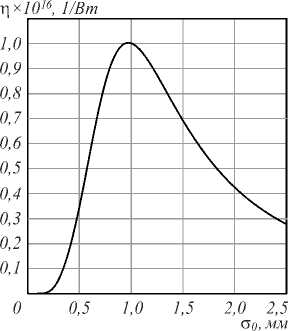
Рис. 5. Зависимость показателя эффективности генерации η вихревого радиопучка от радиуса перетяжки лазерных пучков

Данное обстоятельство обусловливается экстремальной зависимостью интенсивности гауссовских пучков от радиуса перетяжки, которую при заданной мощности излучения Р можно представить в виде:

P      ρ ²

I ~ — ^exp⁽ - ^7).

σ 2 σ 2

Таким образом, показано, что с увеличением длины нелинейной среды наблюдается асимптотическое поведение показателя эффективности рассматриваемого преобразования, что дает возможность определять геометрические размеры преобразующего устройства. С увеличением разности частот эффективность генерации повышается. Проведенные расчеты позволяют подобрать технические параметры преобразователя в зависимости от рассматриваемой системы. Наблюдаемые зависимости находятся в качественном согласии с работой [6].

Полученные результаты можно использовать при построении перспективных высокоскоростных гибридных систем передачи RoF [19] преимущественно субмиллиметрового и микроволнового диапазона, использующих орбитальный угловой момент в качестве дополнительного параметра для кодирования и мультиплексирования мультимедийных данных. Это позволит избежать сложных систем преобразования вихревых оптических пучков в радиопучки с сохранением вихревого волнового фронта электромагнитной волны.

Заключение

В данной работе на основе модифицированной модели трехволнового смешения оптического излучения в нелинейной среде с нелинейной проницаемостью второго порядка рассмотрен процесс конвертирования вихревых пучков оптического диапазона в вихревые пучки радиодиапазона. Показано, что при генерации разностной частоты топологический заряд генерируемого вихревого пучка равен разности зарядов вихревых пучков оптической накачки. Результаты имитационного моделирования процесса показывают асимптотическое поведение показателя эффективности генерации в зависимости от длины нелинейной среды, увеличение эффективности генерации при росте разности частот, определяющей частоту радиовихревого пучка, а также экстремальное поведение показателя эффективности от радиуса перетяжки лазерных пучков накачки. Следует отметить, что перспективным направлением работ в данной области может оказаться использование пучков Бесселя–Гаусса с дробным топологическим зарядом [9, 18].

Исследование выполнено за счет гранта Российского научного фонда (проект № 18-19-00123).