Координация Zn-ТФП со слабыми основаниями / нуклеофилами. Метод «приближений»

Ранее [1], [2], [3], [4], [5], [6] мы описывали координационное взаимодействие металлопорфи-ринов (МП) с различными классами n-донорных лигандов в хлороформе, используя кинетические и термодинамические характеристики процесса, полученные методом электронной спектроскопии (ЭСП). В основе расчетов при этом лежало вычисление коэффициента экстинкции комплекса (ε) при постепенном добавлении к МП лиганда до тех пор, пока положение максимума полосы поглощения не становилось постоянным. Однако, чем более слабым основанием / нуклеофилом является лиганд, тем большее его количество требуется для полного перевода МП в комплекс, а значит, тем в большей степени будут изменяться такие свойства раствора, как дипольный момент, диэлектрическая постоян- ная, а в некоторых случаях – состав и даже строение комплексов. Так, при добавлении к цинк (II)-тетрафенилпорфирину (Zn-ТФП) лиганда в некоторый момент может стать существенной координация МП с его второй молекулой (образование билигандного комплекса). Если же этот лиганд является кислотой Бренстеда – Лоури (как спирты), то по мере увеличения ее концентрации должна возрастать роль специфических взаимодействий, в частности с участием атомов азота МП.

При исследовании комплексообразования Zn-ТФП даже с предельными спиртами для полного перевода МП в комплекс требуется очень большой избыток лиганда (30000 ÷ 150000), и это может повлиять на достоверность определения значений ε и Δ λ _max комплекса. Поэтому нами

были рассчитаны кинетические и термодинамические параметры комплексообразования Zn-ТФП с такими слабыми основаниями/нуклеофи-лами, как спирты, эфиры, альдегиды и кетоны, компьютерным подбором коэффициентов экстинкции комплексов, удовлетворяющих изменениям электронных спектров при гораздо более низком избытке лиганда: от 1 ÷ 700 до 1 ÷ 7000 (для трет-бутилового спирта до 1 ÷ 12 000). Этот способ расчета мы назвали методом «приближений».

После математических преобразований выражения

_ [ Zn-ТФП • L ] = [ Zn -ТФП ] - [ L ]

(при условии С_L >>  C _Zn-ТФП , принимая, что [ L ] ~ С_L ) мы получили равенство:

К =

(DЛк £пЛк " Сп " 1 У^пЛп ^кЛп ) (^кЯк — £пЛк )•( D Лп — £кЛп " Ск " 1 )•[L]

и выразили равновесную молярную концентрацию лиганда

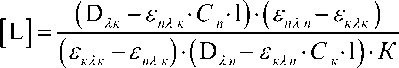
где К – константа устойчивости комплекса, C_n и С_к – равновесные молярные концентрации Zn-ТФП и комплекса; D_λп и D_λк – оптическая плотность в максимуме поглощения Zn-ТФП и комплекса; ε_{п ( λп )} – коэффициент экстинкции Zn-ТФП в максимуме поглощения Zn-ТФП; ε_{п ( λк )} – коэффициент экстинкции Zn-ТФП в максимуме поглощения комплекса; ε_{к ( λп )} – коэффициент экстинкции комплекса в максимуме поглощения Zn-ТФП; ε_{к ( λк )} – коэффициент экстинкции комплекса в максимуме поглощения комплекса; l – толщина оптического слоя.

В этом уравнении содержатся три неизвестных параметра: К , ε_{к ( λ Zn-ТФП max)} и ε_{к ( λк max).} Дальнейший расчет констант устойчивости проводили по методу минимизации в среде Excel с использованием надстройки «Поиск решения».

Суть данного метода заключается в том, что для каждой опытной пробы с экспериментально определенными значениями оптической плотности и заданной концентрацией лиганда компьютер рассчитывает значения К, εк (λ Zn-ТФП max) и εк (λк max) таким образом, чтобы сумма рассчитанных равновесных молярных концентраций лиганда в опытных образцах показывала наименьшее отличие от экспериментальных. Для того чтобы воспользоваться данным методом расчета констант устойчивости, необходимы эмпирические концентрации лиганда, исходная молярная концентрация Zn-ТФП, величина εZn-ТФП (λк max) и значения D в двух максимумах поглощения. После ввода перечисленных данных на рабочий лист Excel задавали произвольные значения К, εк (λ Zn-ТФП max) и εк (λк max), например, равными 1. Далее с использованием функции «Поиск решения» осуществляли минимизацию по суммарному отличию экспериментальных и рассчитанных концентраций лиганда (Σ∆Сi = (Сi (эксп) – Сi (расч))2). Кроме того, такой способ расчета констант устойчивости требует введения ряда ограничений, которые необходимо учитывать, исходя из экспериментальных данных, а именно:

• 1.    К ≥ 0,1 л ∙ моль^–1;

• 2.    Из всех ранее полученных нами спектральных характеристик Zn-ТФП и его n, v-комплексов следует, что ε Zn-ТФП ( λк max) ≤ ε к (λ Zn-ТФП max);

• 3.    ε_{к ( λк max)} ≥ 20000 л ∙ моль^–1 ∙ см^–1 (самое низкое значение коэффициента экстинкции полученного нами n, v-комплекса.

Приведенные в табл. 1 значения констант устойчивости комплексов, рассчитанных нами обычным способом (А) [6] и методом «приближений» (Б), являются очень близкими для таких классов лигандов, как первичные, вторичные и третичные амины, пиридины и гетероарома-тические N-оксиды (сильные электронодонорные лиганды). Эти классы соединений образуют довольно прочные комплексы с Zn-ТФП (К ~ 292–105000 л ∙ моль–1). Поэтому вычисление их коэффициентов экстинкции не требует создания высоких концентраций лигандов.

Несмотря на более слабую нуклеофильность (К 12–180 л∙моль^–1) некоторых гетероароматиче-ских N-оксидов (например, N-оксида 4-нитро-пиридин), анилинов и непредельных третичных аминов (например, триаллиламин), константы устойчивости их комплексов с Zn-ТФП совпадают друг с другом в пределах погрешности расчетов. С другой стороны, для комплексов Zn-ТФП со спиртами, простыми и сложными эфирами, являющимися еще более слабыми электронодонорными лигандами, константы устойчивости комплексов (0,56–11,7 л ∙ моль^–1), рассчитанные двумя методами, обнаруживают тем бóльшие отличия, чем ниже их значения. При этом почти во всех случаях значения К , рассчитанные методом (Б), имеют более высокие значения, а для простых и сложных эфиров (самые слабые нуклеофилы в табл. 1) отличаются в 1,5–2,5 раза. Для спиртов между значениями К , рассчитанными двумя методами, выполняется следующее соотношение lg K _(Б) = 1,12 ∙ lg K _(А) – 0,0597 ( n 7, r 0,90). Подтверждением этого является и тот факт, что использование полученных нами методом (А) констант устойчивости комплексов Zn-ТФП с N-оксидами пиридинов ( n = 5) в чистом и содержащем 3 % этанола хлороформе дает на графиках lg K – pK_a ( σ ) близкие к параллельным прямые.

Методом (Б) нами вычислены К при нескольких температурах, что позволило определить термодинамические характеристики процесса

Таблица 1

Значения констант устойчивости ( К ) комплексов Zn-ТФП с n-донорными лигандами при 25 °C и термодинамических параметров процессов комплексообразования, рассчитанные обычным методом (А) и методом «приближений» (Б)*

№	Лиганд	К , л ∙ моль–1 (А)	К , л ∙ моль–1 (Б)	–ΔH0, кДж ∙ моль–1 (А)	–ΔH0, кДж ∙ моль–1 (Б)	ΔS0, Дж ∙ моль–1K–1 (А)	ΔS0, Дж ∙ моль–1K–1 (Б)
1	DABCO	105000 ± 1700	105000 ± 3900	14,85 ± 0,65	14,72 ± 0,74	46,3 ± 1,5	48,0 ± 3,0
2	н-бутиламин	15210 ± 300	15830 ± 620	11,85 ± 0,51	12,89 ± 0,51	40,0 ± 1,7	36,5 ± 3,0
3	4-метилпиридин	6480 ± 240	6820 ± 230	14,36 ± 0,59	13,91 ± 0,24	25,0 ± 1,6	27,0± 1,0
4	3-метилпиридин	4660 ± 240	4740 ± 110	15,6 ± 0,6	14,61±0,11	18,1 ± 0,1	21,4 ± 0,7
5	N-оксид 4-метокси-пиридина	2470 ± 63	2840 ± 150	13,94 ±0,26	13,42 ± 0,59	19,0 ± 0,8	21,0 ± 1,6
6	ди-н-пропиламин	1360 ± 24	1390 ± 40	18,13 ± 0,28	18,04 ± 0,48	–1,52 ± 0,65	–1,2 ± 1,0
7	N-оксид 3-метилпи-ридина	1030 ± 11	1140 ± 40	13,82 ± 0,31	13,30 ± 0,51	11,4 ± 0,7	14,0 ± 1,0
8	N-оксид 2-метил-4-хлор хинолина	292 ± 4	318 ± 25	12,02 ± 0,32	13,90 ± 0,39	7,2 ± 0,6	10,5 ± 1,1
9	метилдиоктиламин	170 ± 3	174 ± 3	17,16 ± 0,61	16,70 ± 0,56	–14,7 ± 1,3	–12,9 ± 0,9
10	N-оксид 4-нитропи-ридина	134 ± 3	140 ± 6	13,74 ± 0,15	13,60 ± 0,41	–5,7 ± 0,4	–4,8 ± 1,2
11	4-броманилин	109 ± 3	122 ± 10	15,62 ± 0,15	16,34 ± 0,11	–13,2 ± 0,3	–17,3 ± 1,0
12	3-хлоранилин	72 ± 2	72 ± 1	14,59 ± 0,11	15,17 ± 0,19	–13,4 ± 0,3	–15,2 ± 0,8
13	3-нитроанилин	49 ± 1	52 ± 2	14,87 ± 0,19	14,82 ± 1,49	–17,3 ± 0,6	–16,8 ± 4,5
14	ди-циклогексила-мин	48,5 ± 0,6	47,1 ± 0,5	16,95 ± 0,81	14,55 ± 1,04	–24,6 ± 1,3	–17,0 ± 3,0
15	N-пропаргиланилин	40,5 ± 1,5	36,1 ± 3,1	14,52 ± 0,29	14,20 ± 0,61	–17,6 ± 0,9	–16,4 ± 1,1
16	2,5-дихлоранилин	29,8 ± 0,9	30,2 ± 2	14,40 ± 0,41	14,62 ± 0,22	–20,2 ± 1,3	–20,8 ± 0,8
17	2,6-дихлоранилин	3,35 ± 0,12	3,71 ± 0,11	15,5 ± 0,3	14,78 ± 0,19	–40,4 ± 1,3	–39,1 ± 0,7
18	N, N-диметиланилин	20,4 ± 0,8	25,0 ± 1,1	14,78 ± 0,48	15,02 ± 0,51	–24,5 ± 1,3	–23,5 ± 1,5
19	триаллиламин	14,1± 0,2	13,5 ± 0,5	15,33 ± 0,45	14,27 ± 0,27	–29,5 ± 1,9	–6,0 ± 0,6
20	три-н-бутиламин	12,0 ± 0,2	11,0 ± 0,9	19,65 ± 0,57	20,40 ± 1,12	–45,1 ± 2,2	–47,6 ± 2,4
21	4-нитроанилин*	–	12,4 ± 0,3	–	–	–	–
22	диэтиланилин*	–	2,5 ± 0,2	–	–	–	–
23	метанол	7,3 ± 0,2	7,8 ± 0,5	15,14 ± 0,24	13,84 ± 0,71	–35,0 ± 1,4	–30,0 ± 2,1
24	этанол	10,1 ± 0,3	11,9 ± 0,3	13,54 ± 0,26	11,36 ± 0,91	–26,7 ± 1,2	–18,0 ± 1,9
25	н-пропанол	9,1 ± 0,2	11,7 ± 0,2	13,63 ± 0,27	12,57 ±0,95	–27,6 ± 1,4	–21,8 ± 0,9
26	н-бутанол	10,2 ± 0,2	11,3 ± 0,1	11,79 ± 0,24	11,11 ± 0,41	–20,5 ± 1,0	–19 ± 1,1
27	н-гептанол	9,5 ± 0,2	11,2 ± 0,2	9,14 ± 0,22	9,25 ± 0,53	–11,9 ± 0,8	–11,0 ± 0,9
28	н-октанол	9,9 ± 0,3	10,7 ± 0,1	10,31 ± 0,24	9,18 ± 0,71	–15,5 ± 0,9	–10,8 ± 1,4
29	н-нонанол	9,7 ± 0,2	10,9 ± 0,2	9,51 ± 0,34	9,42 ± 0,21	–13,0 ± 2,0	–11,8 ± 0,3
30	диэтиловый эфир	1,26 ± 0,08	3,1 ± 0,2	15,72 ± 0,39	11,74 ± 0,25	–50,4 ± 3,1	–30,3 ± 1,5
31	метилацетат	0,98 ± 0,07	0,62 ± 0,02	11,16 ± 0,42	7,83 ± 2,11	–38,5 ± 2,9	–30 ± 7
32	γ-бутиролактон	0,56 ± 0,02	0,94 ± 0,02	14,00 ± 0,18	11,19 ± 0,71	–52,2 ± 1,5	–38,0 ± 2,7

Примечание: * – методом (А) не удалось определить значения К, для 4-нитроанилина зависимость К от температуры практически отсутствует.

координации при меньшем, чем при использовании способа (А), изменении (в течение эксперимента) природы раствора. Как видно из табл. 1, они, как и значения констант устойчивости, могут существенно различаться в случае очень слабых оснований / нуклеофилов (спирты, простые и сложные эфиры), причем во всех случаях величины ∆H0 и ∆S0, рассчитанные методом (А), являются более низкими (у эфиров различия в ∆H0 доходят до 4, а ∆S0 – даже до 20 единиц, как в случае этоксиэтана), чем при использовании метода «приближений». Как отмечалось выше, это обусловлено особенностями в опре- делении εк (λZn-ТФПmax) и εк (λкmax), вызванными изменением свойств растворителя (среды) из-за создания 30 000 ÷ 200 000 кратных избытков лигандов, требуемых для полной закомплексованности Zn-ТФП. Однако для спиртов между ∆H0 и ∆S0, рассчитанными методами (А) и (Б), все-таки соблюдаются линейные зависимости

(∆ H ⁰ = 0,747 ∙ ∆ H ⁰ ∆ S ⁰ (А ⁽ ) ^Б–⁾ 0,856, r 0,95)⁽.^А)

– 2,10, r 0,96; ∆ S ⁰ _(Б) = 0,775 ∙

Очень часто органические соединения (на-

пример, изониазид и 4-нитроанилин в хлороформе) имеют растворимость, недостаточную для того, чтобы полностью перевести Zn-ТФП в комплекс и определить значения ε последнего. Однако, воспользовавшись методом «приближений», нам удалось рассчитать значения констант устойчивости для некоторых комплексов Zn-ТФП с подобными лигандами (см. табл. 1); для 4-нитроанилина К равно 12,3 л∙моль–1. Для проверки надежности полученного значения мы внесли его в уравнение lgK = 0,31 pKa + 0,82 (n 12, r 0,97) [5], и оказалось, что коэффициент корреляции даже несколько улучшился (lgK = 0,32 pKa + 0,78 (n 13, r 0,98)).

Таким образом, метод «приближений» позволяет получать все необходимые количественные характеристики процессов комплексообразования, не прибегая к использованию чрезвычайно больших концентраций лиганда.

Мы решили проверить, насколько полученные нами значения констант устойчивости молекулярных комплексов Zn-ТФП соответствуют значениям нуклеофильности и электронодонорной способности лигандов / оснований / нуклеофилов / субстратов, определяемых параметрами предложенных ранее в литературе уравнений.

Уравнением Литвиненко коррелируются параметры n , введенные Холлом [7] для третичных аминов. Этот факт свидетельствует о том, что величины n не могут считаться простой характеристикой нуклеофильности реакционного центра, поскольку в них содержится также стерическая составляющая [10; 294]. В 1977 году А. В. Пальм отметил, что «следует признать в общем несостоятельной саму процедуру обработки данных в соответствии с уравнениями типа Бренстеда, Свена – Скотта или Эдвардса.

В качестве корректной процедуры можно рассматривать корреляции в соответствии с уравнениями, учитывающими эффекты заместителей, данные для неизменной пары центров нуклеофильности и электрофильности при варьировании заместителей у этих центров, если таковые имеются. Лишь после такого выделения эффектов заместителей могут быть получены величины (соответствующие lg k°), пригодные для отыскания параметров, характеризующих нуклеофильность и электрофильность реакционных центров» [10].

К сожалению, до настоящего момента так и не была предложена корректная процедура оценки таких параметров. Поэтому созданная нами шкала [1], основанная на параметрах, характеризующих образование аксиальных комплексов Zn-ТФП с n-донорными лигандами, по-видимому, является полезной и перспективной для количественного сравнения нуклеофильности органических соединений.

Традиционно используемая шкала Гутмана (для оценки электронодонорной способности) 180 растворителей [13] характеризует их основность по Льюису или способность акцептировать атом водорода при образовании водородной связи. С одной стороны, донорные числа (DN) Гутмана численно равны –ΔH образования комплексов этих молекул с кислотой Льюиса SbCl ₅ состава 1:1 в 1,2-дихлорэтане. С другой стороны, критерием [9] электронодонорной способности органических оснований могут быть термодинамические характеристики процесса их координации металлопорфиринами, например, синтетическим симметрично замещенным Zn-TФП (гораздо более слабой кислотой Льюиса, чем SbCl ₅ ), периферийные C ₆ H ₅ -заместители которого не оказывают стерических препятствий координации оснований на центральном ионе металла порфирина и специфически не сольватируются электронодонорными молекулами. Поэтому сравнение параметров DN (табл. 2) с K , Δ λ max , Δ H ⁰ и Δ S ⁰ (см. табл. 1) для координации Zn-TФП с теми же лигандами является крайне интересным и целесообразным.

Основность и нуклеофильность основных классов органических соединений в апротонных растворителях типа хлороформа и 1,2-дихлорэтана в первом приближении можно представить в виде следующей последовательности:

фенолы < альдегиды, кетоны, простые и сложные эфиры < анилины < N-оксиды пиридинов < пиридины < предельные амины.

Представленные в табл. 2 величины DN позволяют заключить, что существенные отличия в их значениях наблюдаются в случае сильно различающихся по строению веществ, тогда как для соединений одного и того же класса они довольно близки. В целом изменения значений DN находятся в соответствии с рядом основности /

Таблица 2

Значения чисел (DN) Гутмана [13] для основных классов n-донорых лигандов

Класс n-донор DN Сложные эфиры метилацетат 16,3 γ-бутирлактон 18,0 Простые эфиры диэтиловый эфир 19,2 1,4-диоксан 14,8 Спирты метанол 19 (30) этанол 32 пропанол-2 36 бутанол-1 29 2-метилпропанол-2 38 3-метилбутанол-1 32 н-октанол 32 Анилины анилин 35 2-хлоранилин 31 N-метиланилин 33 N-этиланилин 33 N, N-диметиланилин 27 N, N-диэтиланилин 33 N-оксиды пиридинов N-оксид пиридина 32 N-оксид 4-метилпиридина 36 N-оксид 4-метокси-пиридина 41 Пиридины пиридин 33,1 4-метилпиридин 34 Первичные амины метиламин 39 этиламин 40 н-пропиламин 38 изо-пропиламин 57,5 н-бутиламин 42 трет-бутиламин 57,5 этилендиамин 55 Вторичные амины диметиламин 51 диэтиламин 50 ди-н-пропиламин 40 пиперидин 40 Третичные амины триметиламин 64 триэтиламин 61 три-н-бутиламин 50 диметилбензиламин 21 аммиак 59 (42) Хинолины хинолин 32 нуклеофильности, приведенным выше, и нашей шкалой нуклеофильности / основности, однако есть и противоречия. Например, у диэтилового эфира (DN 19,2) параметр Гутмана выше, чем у диоксана (DN 14,8). Полученные же нами значения констант устойчивости К изменяются в обратной последовательности и составляют соответственно 1,23 и 46 л∙моль–1. У н-октано-ла (DN 32; К = 11,7 л∙моль–1) значение DN меньше, чем у 2-метилпропанола-2 (DN 38; К = 6,1 л∙моль–1), но согласно стерическим факторам и полученным нами данным эффект должен быть обратным; у N, N-диэтиланилина (DN 33; K = 2,5 л∙моль–1) – выше, чем у N, N-диметила-нилина (DN 27; К = 20,4 л∙моль–1), мы же в первом случае из-за низкой нуклеофильности лиганда методом (А) не смогли определить константу устойчивости, а у пиперидина (DN 40; К = 49 700 л∙моль–1) – меньше, чем у трет-бути-ламина (DN 57,5; K = 3510 л∙моль–1) и даже три-н-бутиламина (DN 50; K = 12,0 л∙моль–1). В большинстве случаев (за исключением N-оксидов пиридинов: lgK = 0,0534∙DN + 1,205, r 0,9999; DN = 7,48 ∙ ΔλII – 67,35, r 0,9995; n 3) между DN и lgK (Δλ) линейные корреляции даже внутри одного класса соединений отсутствуют.

Таким образом, шкала Гутмана не позволяет получить ясного представления о взаимосвязи между донорной способностью оснований / нуклеофилов и их способностью к образованию молекулярных комплексов, а также вывести корреляционные уравнения, позволяющие количественно предсказывать реакционную способность соединений. В основе этой неудачи, на наш взгляд, лежат следующие причины:

• 1.    Чрезвычайное разнообразие используемых растворителей (при малом количестве однотипных объектов) приводит к тому, что образующиеся молекулярные комплексы со SbCl ₅ сложно классифицировать и корректный количественный учет электронных, стерических и других факторов на ΔН⁰ процесса координации становится трудноосуществимым.

• 2.    Пентахлорид сурьмы является очень сильным акцептором электронов, в результате чего контроль за сохранением его чистоты в процессе эксперимента сопряжен с огромными трудностями. Этой же причиной обусловлено существенное нивелирование влияния величины электронной плотности на реакционном центре донора на энтальпию процесса образования молекулярного комплекса. Так, значения DN для анилинов, приведенных в табл. 2, изменяются от 27 до 36, а аммиака и предельных аминов – от 39 до 61 единицы, то есть в достаточно узком диапазоне; для некоторых же соединений они определены очень грубо (DN для аммиака 59 (42), метанола 19 (30)).

Наличие же линейных корреляций в случае гетероароматических N-оксидов (n = 3) при использовании чисел Гутмана можно объяснить высокими (супер-) нуклеофильностью атома кислорода вследствие его пространственной доступности, а также эффективностью статической и динамической поляризации молекулы.

Таблица 3

Данные ЯМР (Δδ) и электронной (ΔλII и lgK) спектроскопии для координации Cd-ТФП и Zn-ТФП с пиридинами

	Пиридины	Cd-ТФП [11]		Zn-ТФП [12]	Zn-ТФП [4] ЭСП
		15 N ЯМР Δδ, м.д.	111Cd ЯМР Δδ, м.д.	15 N ЯМР Δδ, м.д.	ЭСП ΔλII, нм	lgK
1	4-CN	–0,13	9,31	–1,12	13,2	2,90
2	4-COMe	–0,19	6,84	–0,51	14,4	3,33
3	H	0	0	0	15	3,55
4	3-Me	-	-	0,16	15,8	3,67
5	4-Me	0,15	–0,35	0,23	16,1	3,81
6	4-NH2	0,26	–7,86	0,74	17,5	4,24

В предложенной нами шкале нуклеофильности (значения К изменяются от 0,6 до 105 000 л∙моль–1) мы учли перечисленные недостатки: в качестве акцептора используется слабая кислота Льюиса – Zn-ТФП и исследуются только молекулярные комплексы n, v-типа состава 1:1, причем корреляционные уравнения выведены для достаточно больших групп нуклеофилов, относящихся к одному и тому же классу органических соединений. Мы попытались на основании этих уравнений найти сходные черты и различия в кинетическом и термодинамическом поведении различных классов азот- и кислородсодержащих доноров в качестве нуклеофилов / лигандов / субстратов, и нам удалось обнаружить неизвестные ранее закономерности [1], [2], [3], [4], [5], [6].

Предложенный нами новый подход к оценке нуклеофильности молекул на основе данных, характеризующих устойчивость их комплексов с МП, несомненно имеет массу достоинств. Однако значения констант устойчивости, полученные методами электронной и флуоресцентной спектроскопии, близки между собой, но сильно отличаются от тех, которые оценены с помо -щью ЯМР-спектроскопии и особенно калориметрии [8].

Прежде всего оказалось, что данные метода ЯМР не согласуются с другими спектроскопическими результатами. В работах [11], [12] представлены результаты 15N- и 111Cd ЯМР-спек-троскопии в хлороформе для молекулярных комплексов Zn-ТФП и Cd-ТФП с 3-, 4-замещен-ными пиридинами.

Их сопоставление с нашими данными, вычисленными методом ЭСП [3], выявило, что между изменениями химических сдвигов (Δδ) в ЯМР-спектроскопии, смещениями положений максимумов полос поглощения (Δλ) и lgK в ЭСП выполняются следующие линейные корреляции:

для Cd-ТФП (n = 5) lgK = 2,43 ∙ Δδ ^{15 N} + 3,52 r 0,91 Δλ _II = 1,03 ∙ Δδ ^15N + 12,15 r 0,99

lgK = 0,07 ∙ Δδ ^111Cd + 3,68 r 0,97 Δλ _II = 0,234 ∙ Δδ ^111Cd + 15,61 r 0,97

для Zn-ТФП (n = 6) lgK = 0,688 ∙ Δδ ^15N + 3,64 r 0,99 Δλ _II = 2,25 ∙ Δδ ^15N + 15,52 r 0,98

Следовательно, величины Δδ (в комплексах Zn-ТФП они более чувствительны, чем Cd-ТФП, к изменениям электронной плотности на атоме донора) в ядерном магнитном резонансе, как и Δλ в электронной спектроскопии, можно использовать для оценки основности / нуклеофильности лигандов, способных к образованию молекулярных комплексов n, v-типа и состава 1:1. Таким образом, изменения Δδ пространственно доступных атомов донора и акцептора, принимающих непосредственное участие в образовании новой связи, правильно характеризуют электронные эффекты заместителей, влияющие на устойчивость молекулярных комплексов. Другое дело, что методы расчета констант устойчивости комплексов на основании изменений химических сдвигов атомов, стерически затрудненных или удаленных от донорно-акцепторной связи, обычно используемые в литературе, требуют корректировки, учитывающей и другие эффекты (например, стерические, гидрофобные и т. д.). Не исключены случаи, когда расчеты констант устойчивости на основании изменений химических сдвигов невозможны (например, при независимости Δδ удаленных от донорно-акцепторных центров атомов от природы заместителя) или же приводят к неверным результатам (в случае изменения Δδ по мере увеличения концентрации лиганда за счет конкурентного образования других комплексов).

Например, в ряду гетероароматических N-оксидов подобные ошибки возможны при изучении координации с N-оксидами 4-(4-ди-метиламиностирил) – и 2,6-диметил-4-нитро-пиридинов: в первом случае за счет образования n, v-комплекса с участием диметиламиногруппы, а во втором – π, π-комплексов между порфириновой системой и молекулами лиганда. Действительно, согласно данным работы [8], константа устойчивости комплекса Zn-ТФП с N-оксидом 2,6-диметил-4-нитропиридина, определенная методом ЯМР, равна 5622, в то время как в электронных спектрах МП не происходит видимых изменений даже при очень большом избытке лиганда. Последний факт свидетельствует о чрезвычайно слабой донорно-акцепторной связи Zn – O и согласуется с низкими электронной плотностью и пространственной доступностью атома кислорода в указанном соединении.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Электронные спектры снимали на приборе СФ 2000-02. Константы устойчивости Zn-ТФП с пиридинами в хлороформе методом (А) определяли, как описано в работе [6].

Термодинамические константы процесса комплексообразования рассчитывали графиче- ским методом с учетом формулы (первое приближение Улиха):

lnK _T = -ΔH⁰ ₂₉₈ / RT + ΔS⁰ ₂₉₈ / R, предполагая, что в исследуемом узком интервале температур (273–313 К) значения ΔH и ΔS остаются постоянными.

COORDINATION OF ZN-TPHP WITH WEAK BASES / NUCLEOPHILES.

METHOD OF “APPROXIMATION ALGORITHM”