Коррекция динамической погрешности инерционных детекторов газоаналитических приборов

Известные детекторы газоаналитических приборов [1,2] обладают повышенной инерционностью, которая затрудняет их использование в системах экспресс - анализа содержания примесей в газовой среде. Большая инерционность этих детекторов вызвана, с одной стороны, значительной величиной объема камеры детектора, с другой – длительностью процесса установления теплового равновесия в газовом потоке между термочувствительным элементом и стенкой камеры детектора. Этот фактор вызывает появление динамической погрешности определения концентрации примеси в потоке газа.

Целью работы является разработка математического метода коррекции указанной динамической погрешности.

МЕТОДИКА ИССЛЕДОВАНИЙ

При динамических измерениях интерес представляет не выходной сигнал детектора y ( t ), а контролируемый входной параметр детектора x ( t ). Поэтому задачей коррекции сигнала y ( t ) является определение значений параметра x ( t ) с учетом оператора А , характеризующего динамические свойства детектора и его аппаратную функцию. В современных измерительных системах доступны дискретные значения сигнала y ( t ), формируемые аналого - цифровым преобразователем системы.

Такая задача может быть решена реализацией оператора А^-1 , обратного оператору А при соответствующей обработке дискретных значений сигнала y ( t ) [3].

В наиболее распространенном случае инерционный детектор имеет передаточную функцию апериодического звена первого порядка

W ( р ) = y T p ) = 7 K ,        (1)

x ( p ) Tp + 1

где Т – постоянная времени детектора.

При К =1 передаточная функция корректирующей цепи принимает вид

W ^ч( р ) = z ^= Tp + 1 ■

У ⁽ p )

что соответствует реализуемому дифференциальному уравнению dy(t) z (t) = T       + у (t).

dt

Таким образом, это метод коррекции динамической погрешности должен реализовать функцию дифференцирования сигнала y ( t ) и сложения его производной с самим сигналом.

Для решения такой задачи в [3] было предложено использовать цифровой фильтр, реализующий параболическую сплайн – аппроксимацию дискретных значений сигнала y ( t ), а также его производной.

При использовании параболической сплайн – аппроксимации на n-м дискретном участке сигнал описывается параболической функцией yn (t) = a 2 [ n ] t2 + a1 [ n ] t + a 0 [ n ] , где a2, a 1, a0 - коэффициенты аппроксимирующей функции.

Коэффициенты такой аппроксимации могут быть определены с использованием цифровых фильтров «скользящей» обработки дискретных значений сигнала y ( t ) в реальном темпе времени, число точек весовых функций фильтров обычно лежит в пределах 4…6.

Коэффициенты цифровых фильтров пятиточечной сплайн - аппроксимации сигнала y ( t ) по его дискретным значениям, определяются выражениями [4]:

^а 0 [ ⁿ ] = 116 ( ^- у [ ^{n - 2} ] ^{+ 4} у [ ^{n -} 1 ] + ¹⁰ у [ ⁿ ] ^{+ 4} у [ ^{n +} 1 ]^- у [ ^{n + 2} ] ) , a ₁ [ n ] = 18 ( у [ n - 2 ] - 6 у [ n - 1 ] + 6 у [ n + 1 ] - у [ n + 2 ] ) ,(2) а 2 [ ^п ] = Хб ( - у [ ^п - 2 ] + 7 у [ ^п - 1 ] - 6 у [ n ] - 6 у [ n + 1 ] + 7 у [ n + 2 ] - у [ n + 3 ] ) .

Коэффициенты пятиточечной параболической сплайн-функции, аппроксимирующей производную сигнала y ( t ) , определяются выражениями [4]:

bо [n ]=Х2 (у [n - 2]-8 у [n - 1]+8 у [n+1]-у [n+2]),

b1[ n ]=}6 (- x [ n - 2]+10 x [ n -1]-18 x [ n ]+10 x [ n+1]-x [ n+2]) ,(3)

b2 [ n ] = ^2 ( у [ n" 2]" 9 у [ n -1]+22 у [ n ]-22 у [ n+1]+9 у [ n+2]-у [ n+3])

Таким образом, скорректированный сигнал определяется выражением z (t) = c 2[ n ] t2 + c1[ n ] t + c 0[ n ],(4)

где c0[n] = a0 [n] + T ■ b0 [n] ,

• c1[ n ] = a1 [ n ] + T ■ b1 [ n ],(5)

c ₂[ n ] = a ₂ [ n ] + T ■ b ₂ [ n ] .

При t =0 из (4) следует:

• z(n) = c0[n] = a0 [n] + T ■ b0 [n] .(6)

Как видно из (3), скорректированный сигнал z ( t ) формируется относительно дискретных значений сигнала y ( n ) детектора с задержкой в 2 дискретных интервала.

Профиль скорректированного сигнала (4) в идеальном случае должен соответствовать профилю входного параметра x ( t ).

Использование сплайн-аппроксимации позволяет определить значения сигнала z ( t ) внутри интервалов дискретизации, что является достоинством рассматриваемого метода.

Рассмотрим в качестве примера коррекцию сигнала микродетектора по теплопроводности, широко распространенного в расходомерах микропотоков газов, в газоаналитических приборах, в хроматографических анализаторах.

Переходная характеристика одного из таких детекторов [5] изображена на рис. 1. В соответ-

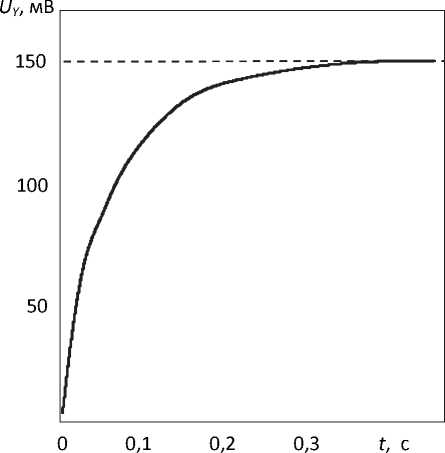
Рис. 1. Диаграмма выходного сигнала U_Y микродетектора по теплопроводности при скачкообразном входном параметре x ( t ) = 1( t )

ствии со стандартной методикой [6] определения инерционности детектора по его переходной характеристике постоянная времени Т детектора в выражении (1) оказалась равной 0,1с.

Известно [6,7], что концентрация введенной в газовый поток примеси в виде импульса распределяется в соответствии с функцией, близкой к Гауссовой. Это объясняется протеканием ряда физических процессов, основным из которых является процесс диффузии. При протекании газового потока через камеру детектора по теплопроводности детектор формирует сигнал y ( t ) в соответствии с величиной мгновенной концен-

трации примеси в потоке, однако инерционность детектора вызывает появление динамической

погрешности.

Рассмотрим коррекцию выходного сигнала

такого детектора при его входном параметре,

изменяющемся в соответствии с Гауссовой функ-

цией единичной высоты (рис. 2)

x ( t ) = exp[ —

( t — 0.05)² 0.015 ]

Ширина такой функции составляет примерно 0,05с.

При передаточной функции (1) детектора

W (P )= —1—,

Tp + 1

его переходная характеристика определяется t —

выражением h (t) = (1 — e T ).

Выражение для сигнала y ( t ) на выходе ИП может быть получено с использованием интеграла Дюамеля:

t

, х 1 Г

y(t) = yl exp(

—

( t — т — 0.05)²

0.015    )

exp( — ^— ) d — .

Для конкретного значения постоянной времени Т =0,1с передаточной функции (1) детектора график этой функции изображен на рис. 2. Как видно из рассмотрения графика, такой детектор характеризуется очень большой динамической погрешностью.

Функция скорректированного сигнала z ( t ) определяется при аппроксимации дискретных значений сигнала y ( t ) параболической сплайн -функцией с использованием выражений (2) – (3) для коэффициентов аппроксимации, а также выражений (4) – (5) для метода коррекции.

Эти функции изображены на рис. 3, при рассмотрении которого видно, что рассмотренный метод достаточно эффективно восстанавливает по форме сигнал x ( t ), действующий на входе инерционного детектора, с запаздыванием в 2 интервала дискретизации.

РЕЗУЛЬТАТЫ

При наличии в потоке газа нескольких примесей, размещенных в потоке на некотором расстоянии друг от друга, детектор регистрирует последовательно два пика, форма которых близка к Гауссовой функции. Такая ситуация характерна для различных хроматографических и ряда других анализаторов. В этом случае инерционность детектора может вызвать существенную динамическую погрешность.

На рис. 4 представлены диаграммы сигналов: входного параметра x ( t ) микродетектора по теплопроводности, сигнала y ( t ), формируемого на выходе детектора, скорректированного сигнала z ( t ) с использованием описанного алгоритма коррекции. Входной параметр x ( t ) в данном случае представляет собой сумму двух Гауссовых функций вида (7), смещенных друг относитель-

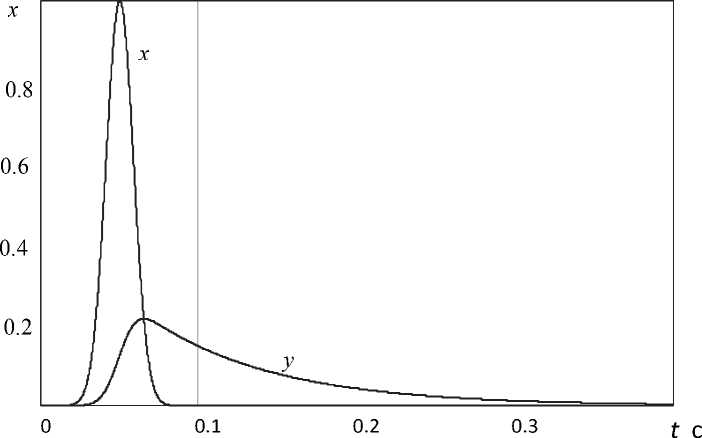
Рис. 2. Сигналы на входе и выходе инерционного детектора: х – график изменения параметра на входе детектора, y – сигнал на выходе детектора

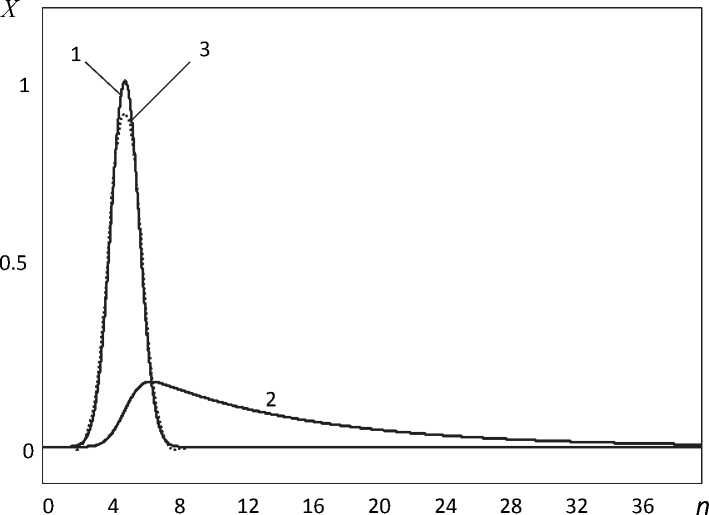
0   0.04 0.08 0.12 0.16 0.2 0.24 0.28 0.32 0.36 t c

Рис. 3. Диаграммы сигналов:

1 - параметр x ( t ) на входе инерционного детектора; 2 - сигнал y ( t ) на выходе детектора;

3 - скорректированный сигнал z ( t-2 ), сдвинутый на 2 дискретных интервала влево

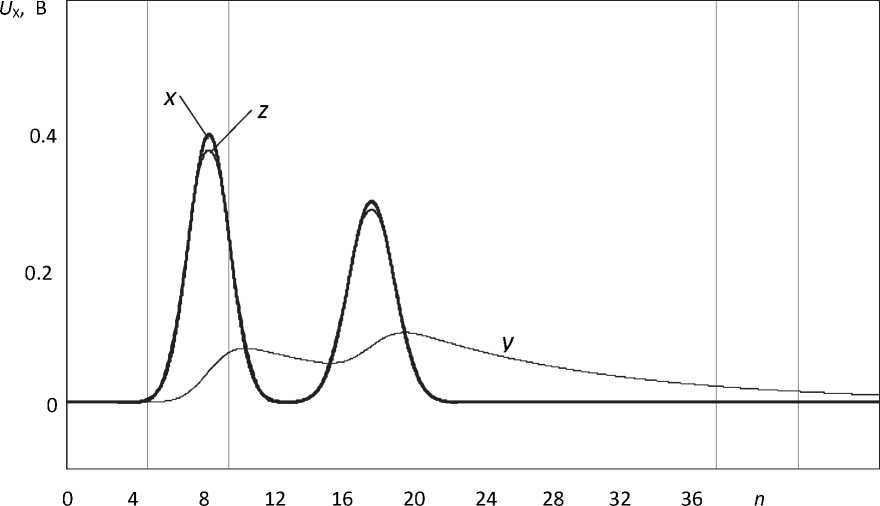
Рис. 4. Коррекция сигнала детектора, представляющего собой две смещенные Гауссовые функции

но друга на интервал 0,02с. Ширина Гауссовых функций составляет примерно 0,06с. Алгоритм коррекции использует параболическую сплайн - аппроксимацию дискретных значений сигнала детектора, интервал дискретизации составляет 0,01 с. Из рассмотрения диаграмм видно, что динамическая погрешность, в данном случае составляющая десятки процентов, с использовани- ем описанного алгоритма коррекции снижается до нескольких процентов.

ЗАКЛЮЧЕНИЕ

Метод коррекции динамической погрешности инерционного детектора по теплопроводности показывает хорошие результаты в случае, когда достаточно точно известна передаточная функция детектора. В том случае, когда передаточная функция представляет собой апериодическое звено первого порядка, динамическая погрешность снижается в значительной степени. Описанный подход может быть применен и в том случае, когда передаточная функция детектора соответствует апериодическому или колебательному звену второго порядка. Метод коррекции, описываемый выражениями (2) – (6), достаточно прост и может быть легко реализован современными микропроцессорными системами.