Коррекция динамической погрешности измерительных преобразователей на основе сплайн-аппроксимации сигнала

Самарский государственный технический университет

Рассмотрен метод коррекции динамической погрешности инерционных измерительных преобразователей с передаточной функцией 1-го порядка с использованием параболической сплайн ‒ аппроксимации дискретных значений сигнала, а также его первой производной.

Динамическая погрешность, присутствующая при измерениях ряда параметров в динамическом режиме, существенно искажает получаемую с первичных измерительных преобразователей (ИП) информацию. Особое значение эта проблема имеет в тепловых измерениях, где используются инерционные преобразователи.

Динамическая погрешность зависит от постоянной времени ИП, а также скорости изменения измеряемой величины и может быть скорректирована с использованием аппаратных и программных методов.

Применение аппаратных методов сопряжено с решением ряда проблем. Снижение динамической погрешности путем уменьшения по стоянной времени ИП, как правило, снижает его надежность и долговременную стабильность. Кроме того, уменьшение тепловой инерционности ИП связано со значительными технологическими трудно стями.

В связи с этим все большее распространение получает коррекция динамических погрешностей с использованием программных методов.

В ряде случаев коррекция динамической погрешно сти представляет собой об- ратную задачу [1], то есть задачу восстановления входного сигнала по известной информации об операторе А (аппаратной функции) ИП.

Рассмотрим задачу измерения мгновенных значений параметра x(t), который преобразуется ИП в сигнал y(t) , формируемый на его выходе (рис.1).

При динамических измерениях, как правило, интерес представляет не выходной сигнал ИП y(t) , а параметр x(t) . Поэтому задачей обработки результатов измерений является определение значений параметра x(t) по выходному сигналу y(t) и оператору А , описывающему динамические свойства ИП, что представляет собой решение задачи коррекции его аппаратной функции. Наиболее просто такая задача решается реализацией оператора А^-1 , обратного оператору А , с использованием корректирующего звена КЗ (рис.1) в аппаратном или программном виде, который обрабатывает сигнал y(t) . Однако по сущности своей такая задача является некорректной, поскольку обратный оператор должен реализовывать функцию предсказания сигнала, что физически реализовать невозможно [1].

В связи с этим корректное решение

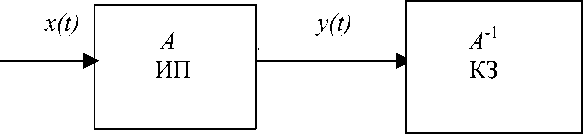
Рис.1. Структурная схема тракта прохождения сигнала

z(t)

обратной задачи при измерениях динамических параметров может быть выполнено, если предусмотреть определенное запаздывание в формировании значений сигнала z(t) на выходе корректирующего звена, что не требует реализации функции предсказания.

В наиболее распространенном случае инерционный ИП имеет передаточную функцию, соответствующую передаточной функции апериодического звена первого порядка

мации.

Коэффициенты пятиточечной парабо-личе ской сплайн‒функции, аппроксимирующей сигнал y(t) по его дискретным значениям, определяются следующими выражениями [2]:

a ₀

[п ]= X

— x [ п — 2 ] + 4 x [ п —1] +

^+ 10 x [ п ] + 4 x [ п + 1 ] — x [ п + 2 ]

a 1 ^{[ п ]} = 1/8

^< x ^{[ п —} 2 ^]— 6 x ^{[ п — 1 ]+ 2} ^+ 6 x [ п + 1 ] — x [ п + 2 ]_?

W (p ) = yM = -K x (p) Tp +1 ’ где Т ‒ по стоянная времени ИП.

При К =1 передаточная функция корректирующего звена принимает вид

W "'

Tdy ) + У ( t ) = z ( t ).

dt

Таким образом, это звено должно реализовать функцию дифференцирования сигнала y ( t ) и сложения его производной с самим сигналом (рис.2).

Для решения такой задачи предлагается использовать цифровой фильтр, реализующий сплайн‒аппроксимацию дискретных значений сигнала y ( t ), а также его производной.

При использовании параболической сплайн ‒ аппроксимации на n -м дискретном участке сигнал описывается параболической функцией (рис.3)

a ₂ [ п ] = 1

^< — x [ п — 2 ] + 7 x [ п — 1 ] — 6 x [ п ]

—

¹⁶ ^— 6 x [ п + 1 ] + 7 x [ п + 2 ] — x [ п + 3 ] "

Коэффициенты пятиточечной парабо-личе ской сплайн‒функции, аппроксимирующей производную сигнала y(t), определяются выражениями [2]:

b ₀ [ п ] = Ц2 ( x [ п — 2 ] — 8 x [ п — 1 ] + 8 x [ п + 1 ] — x [ п + 2 ] ) , b 1 [ п ] = 16 ( — x [ п — 2 ] + 10 x [ п — 1 ] — — 18 x [ п ] + 10 x [ п + 1 ] — x [ п + 2 ] ) ,      (3)

b ₂ [ п ] = Ц2 ( x [ п — 2 ] — 9 x [ п — 1 ] + 22 x [ п ] — — 22 x [ п + 1 ] + 9 x [ п + 2 ] — x [ п + 3 ] ) .

Таким образом, сигнал на выходе корректирующего звена должен иметь вид z (t) = c 2[ п ] t2 + c1[ п ] t + c 0[ п ],        (4)

где c0[п] = a0 [п] + T ■ b0 [п] , c1[ п ] = a1 [п ] + T ■ b1 [п ],             (5)

У п ( t ) = a 2 [ п ] t ² + a _x [ п ] t + a 0 [ п ] ,     (1)

где a₂ , a₁ , a₀ ‒ коэффициенты аппрокси-

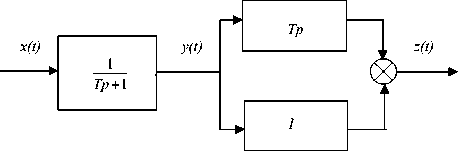
Рис.2. Структурная схема корректирующей цепи

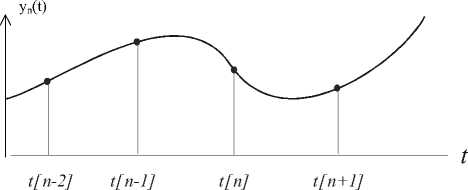
Рис.3. Аппроксимация выходного сигнала измерительного преобразователя параболической сплайн - функцией

c2[n] = a2 [n] + T■ b2 [n].

При t =0 из (8) следует:

z(n) = c0[n] = a0 [n] + T ■ b0 [n]. (6)

Как видно из (3), сигнал z(t) на выходе корректирующего звена формируется с задержкой в 3 дискретных интервала.

Выражение (4) определяет сигнал на выходе корректирующего звена, который в идеальном случае (при отсутствии погрешностей) должен повторять по форме сигнал x(t) .

Использование сплайн‒аппроксима-ции позволяет определить значения сигналов y(t), z(t) внутри интервалов дискретизации, что является достоинством рассмат- риваемого метода.

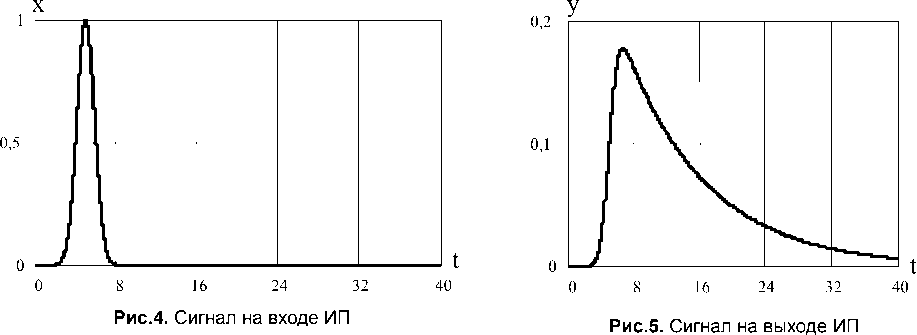
Рассмотрим в каче стве примера прохождение через описанную корректирующую цепь, изображенную на рис.1, единичного сигнала Гауссовой формы (рис.4)

(t - 5)\ x(t) = exp[-v    7 ].

.

При передаточной функции ИП

W (p ) = —1—

Tp +1 , его переходная характеристика определя- t ется выражением h(t) = (1 - e T).

Выражение для сигнала y(t) на выхо-

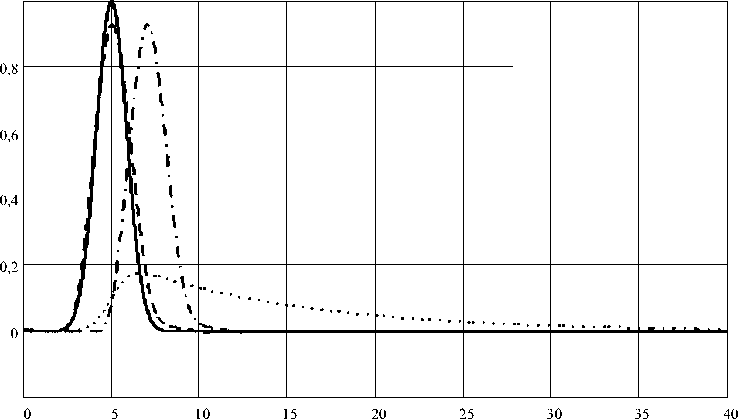
Рис.6. Диаграммы сигналов сигнал x(t) на входе первичного преобразователя сигнал y(t) на выходе первичного преобразователя сигнал z(t) на выходе корректирующего фильтра сигнал z(t-2)

де ИП может быть получено с использованием интеграла Дюамеля:

t

1 г

у(t) = -| exp(-T 0 L

( t - т - 5) 2

1.5

т

) exp ^{( -} т ) d^T .

Для конкретного значения постоянной времени Т =10с передаточной функции ИП график этой функции изображен на рис.5.

При аппроксимации сигнала y ( t ) сплайн ‒ функцией с использованием выражений (2) ‒ (3) для коэффициентов аппроксимации, а также выражений (4) ‒ (5) определяется функция сигнала z ( t ) на выходе корректирующего звена.

Эти функции изображены на рис.6, при рассмотрении которого видно, что рассмотренное корректирующее звено доста- точно эффективно восстанавливает по форме сигнал x(t), действующий на входе инерционного ИП, с запаздыванием в 3 интервала дискретизации.