Коррекция нелинейных искажений в цифровых формирователях сигналов
Автор: Викторов Д.С., Пластинина Е.В.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 3 т.11, 2018 года.
Бесплатный доступ
Предложен метод цифровой коррекции нелинейных искажений, вносимых в зондирующий сигнал аналоговым ключом в формируемые сигналы, позволяющий увеличить реальный динамический диапазон цифрового формирователя сигналов и повысить качество синтезируемых сигналов.
Коррекция нелинейных искажений, аналоговый ключ, цифровой формирователь сигналов, цифровой корректор
Короткий адрес: https://sciup.org/146279363
IDR: 146279363 | УДК: 621.39 | DOI: 10.17516/1999-494X-0046
Текст научной статьи Коррекция нелинейных искажений в цифровых формирователях сигналов
На современном этапе развития радиолокационных средств требуется создание многофункциональных и специализированных РЛС, способных быстро изменять свои характеристики вслед за быстроменяющейся целевой и помеховой обстановкой. Важнейшей составной
Однако ЦФС свойственны нелинейные искажения, возникающие за счет статических и динамических ошибок цифроаналогового преобразования и преобразования формируемого сигнала в аналоговом ключе.
Применение аналоговых ключей (АК) в цифровых формирователях зондирующих сигналов (ЦФЗС) обусловлено рядом причин.
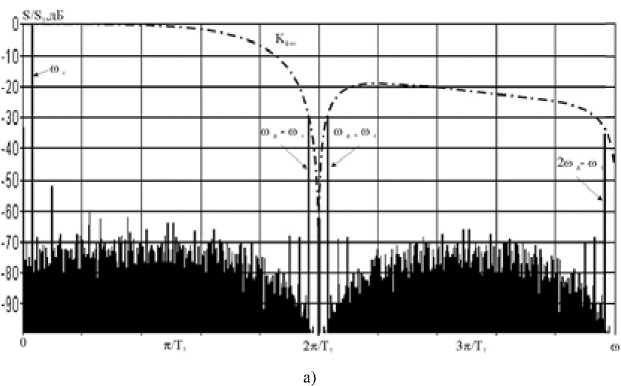
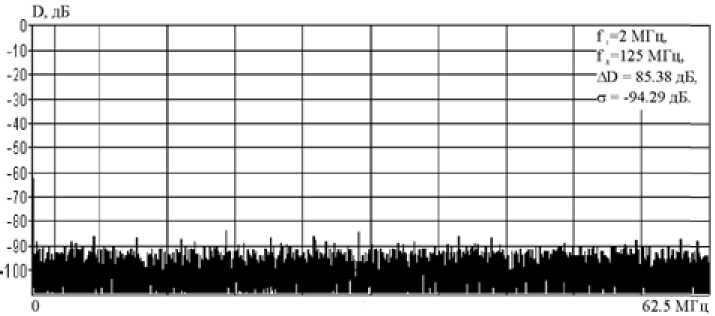
Во-первых, верхняя граница рабочего диапазона современных ЦФЗС, не использующих однополосную балансную модуляцию (ОБМ), не превышает 1/(2 T д ), где T д – период тактового сигнала. Причиной тому является существенная неравномерность амплитудно-частотной характеристики (АЧХ) цифроаналогового преобразователя (ЦАП), на частотах свыше 1/(2 T д ) (рис. 1 а ).
Повышение верхней границы рабочего диапазона ЦФЗС при помощи ОБМ [1] или компенсации боковых составляющих гармоник за счет вычисления выборок формируемого колебания в разные моменты времени [2] требуют наличия квадратурных каналов. К тому же наличие балансного сложения (или вычитания) на выходе не позволяет получить подавление противоположной боковой составляющей в широком диапазоне более чем на 40–50 дБ.
Стробирование формируемого сигнала в АК приводит к тому, что длительность его выборок на выходе АК ( U ак) (рис. 2 в ) становится меньше, чем длительность его выборок на входе АК ( U цап ) (рис. 2 а ).
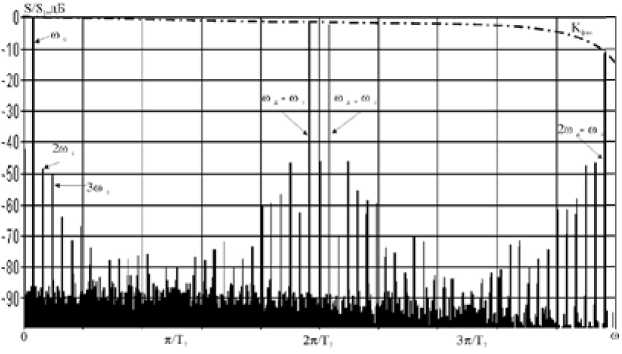
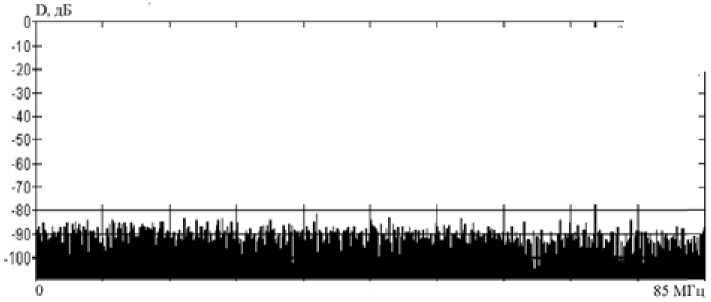
Основной лепесток АЧХ последовательно соединенных ЦАП и АК ( K ф ао) расширяется (рис. 1 б ) по сравнению с АЧХ отдельно взятого ЦАП (рис. 1 а ), что позволяет существенно снизить неравномерность АЧХ ЦФЗС в целом. С учетом дискретного характера спектра формируемого сигнала это дает возможность при помощи полосового фильтра (ПФ) выделять его гармоники из дискретных подспектров, расположенных на частотах более высоких, чем 1/(2 T д) (рис. 1 б ), тем самым увеличивая границы рабочего диапазона ЦФЗС без использования квадратурных каналов.
Во-вторых, при преобразовании цифровых отсчетов синтезируемого сигнала в аналоговые при помощи ЦАП неизбежно возникают динамические ошибки цифроаналогового преобразования, к которым относятся различия во времени включения и выключения уровней квантования ЦАП, а также проникновение управляющих сигналов ЦАП на его выход, через паразитные емкостные и индуктивные связи.
Динамические ошибки цифроаналогового преобразования приводят к появлению большого количества паразитных дискретных составляющих в рабочем диапазоне частот (рис. 1 а ). Причем уровень данных дискретных составляющих растет с увеличением соотношения синтезируемой и тактовой частоты и может достигать – 55–60 дБ.
Результаты исследований показали, что источником динамических ошибок является сигнал управления ЦАП [3]. Из чего следует, что подобные ошибки невозможно устранить известными методами коррекции, так как цифровой метод коррекции предполагает внесение корректирующих поправок в цифровые отсчеты формируемого сигнала, что в свою очередь приводит – 337 –
б)
Рис. 1. АЧХ ЦАП и спектр формируемого сигнала: а – АЧХ отдельно взятого ЦАП и спектр формируемого сигнала без коррекции; б – АЧХ последовательно соединенных ЦАП и АК, и спектр формируемого сигнала с коррекцией
Fig. 1. The amplitude-frequency characteristic of the digital-to-analog converter and a range of the formed signal: a – the amplitude-frequency characteristic of separately taken digital-to-analog converter and a range of the formed signal without correction; b – the amplitude-frequency characteristic of consistently connected digital-to-analog converter and an analog key, and a range of the formed signal with correction к изменению сигнала управления ЦАП, которому будут соответствовать уже новые значения динамических ошибок.
Используя то свойство динамических ошибок, что во временной области они совпадают с моментами переключения ЦАП из одного квантованного значения напряжения формируемого сигнала на его выходе в другое (рис. 2 а ), можно утверждать, что наиболее эффективным методом устранения данного вида ошибок является их стробирование. При этом под воздействием управляющего сигнала (рис. 2 б ) АК на время переходных процессов закрывается и отключает выход ЦАП от выхода ЦФЗС (рис. 2 в ). В результате спектр выходного сигнала очищается от динамических ошибок ЦАП (рис. 1 б ).
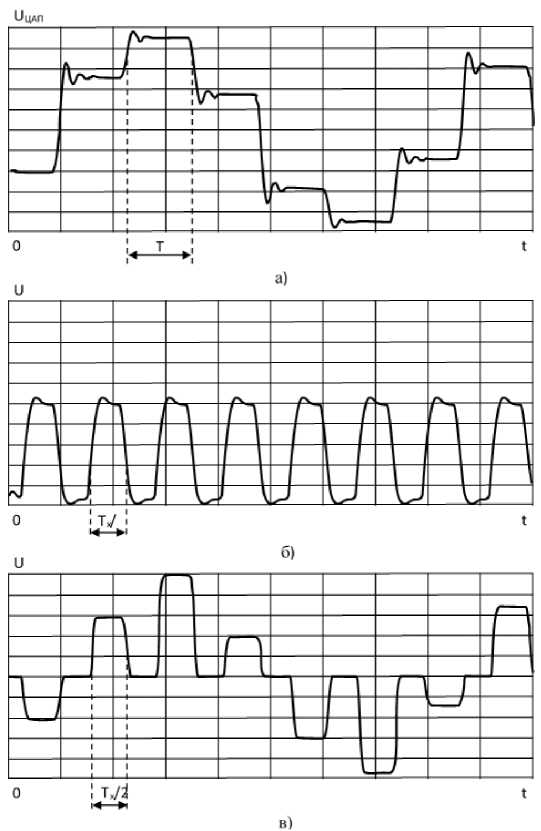
Рис. 2. Сигналы ЦАП: а – сигнал на выходе ЦАП; б – управляющий сигнал; в – скорректированный сигнал на выходе ЦАП
Fig. 2. Signals of the digital-to-analog converter: a – a signal at the exit of the digital-to-analog converter; b – the operating signal; c – the corrected signal at the exit of the digital-to-analog converter
В качестве элементной базы, которая в настоящее время применяется для построения АК, используются полевые транзисторы. Применение данного типа транзисторов обусловлено малым уровнем собственных шумов, соизмеримым с тепловым шумом, высоким входным сопротивлением, малыми токами утечки в цепи управления, свойством обратимости данных электронных приборов и высоким быстродействием.
В результате того, что сопротивление канала полевого транзистора нелинейно зависит от значений напряжения, действующего между стоком и истоком ( U ЦАП) (рис. 2 а ), а также от значения между стоком и затвором ( U У ) (рис. 2 б ) [4], передаточная функция АК является нелинейной. Это приводит к появлению паразитных дискретных составляющих, кратных частоте синтезируемого сигнала (ω с ) в рабочем диапазоне частот (рис. 1 б ). Однако количество дискрет- – 339 –
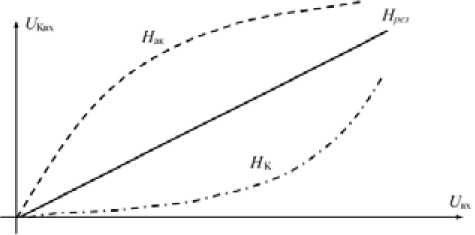
Рис. 3. Графическое представление задачи коррекции нелинейных искажений сигнала на выходе АК
Fig. 3. Graphical representation of correction problem of nonlinear distortions of a signal at the exit of an analog key ных составляющих, требующих коррекции при правильно выбранной амплитуде входного напряжения, а также минимального дифференциального сопротивления канала транзистора, не превышает нескольких единиц.
Задача коррекции нелинейных искажений зондирующего сигнала на выходе АК сводится к тому, чтобы в схему формирования сигнала был добавлен некоторый элемент (корректор), передаточная функция которого являлась бы обратной (рис. 3, Н к) передаточной функции АК (рис. 3, Н а к ). В таком случае результирующая передаточная функция корректора и АК будет представляться в виде прямой линии (рис. 3, Нрез ), что уже говорит об отсутствии продуктов нелинейных искажений сигналов на выходе такой системы.
Линеаризацию результирующей передаточной функции можно осуществить путем применения как аналоговых, так и цифровых корректирующих устройств [5]. Однако аналоговая коррекция обладает рядом существенных недостатков. Основным из них является невозможность осуществления адаптивной коррекции при изменении параметров передаточной функции нелинейного элемента с течением времени под воздействием внешних факторов. Использование аналоговых элементов в корректирующих цепях также требует прецизионной настройки и точного подбора параметров электронных приборов. Из-за чего аналоговые корректоры, по сути, являются уникальными устройствами для каждого из образцов ЦФЗС, пусть даже и однотипных, что позволяет говорить о нетехнологичности такого подхода к коррекции нелинейных искажений.
Цифровые корректоры не имеют указанных недостатков, могут быть размещены непосредственно в формирователе цифровых отсчетов (ФЦО) ЦФЗС и обладать передаточной функцией, обратной передаточной функции АК. В таком случае задача коррекции нелинейных искажений, вносимых АК, сводится к определению параметров передаточной функции корректора.
Пусть передаточная функция АК аппроксимируется степенным полиномом, тогда дискретные отсчеты сигнала на его выходе представляются следующим выражением:
U ак = 2 a 1 r U ак вх ) , (1) r = 1
где U – отсчеты сигнала на входе АК; ar – коэффициенты степенного полинома, аппроксими-вх рующего передаточную функцию АК, идентифицировать которые можно по результатам измерения параметров продуктов, нелинейных искажений [6]; Uак – отсчеты сигнала на выходе АК.
Передаточная функция корректора также представляется степенным полиномом, и дискретные отсчеты! сигнала на его выходе, соответственно, таковы:
'
U к -^ квх Ь (2)
где jк - отсчеты сигнала на входе корректора; bi - коэффициенты степенного полинома, вх аппроксимирующего передаточную функцию корректора; U – отсчеты сигнала на выходе к корректора.
Так как используется цифровой метод коррекции, то корректирующее устройство размещается перед нелинейным элементом, коим является аналоговый ключ (рис. 4). В таком случае отсчеты формируемого сигнала на выходе аналогового ключа представляются следующим выражением:
D D йак = Хаr-йK = XО'r- ^jj‘ квх
r
• (3)
Предполагая, что при определении параметров передаточной функции корректора, аппроксимируемой бесконечным в общем случае степенным рядом, удерживаем m первых его членов, выражение (3) с учетом формулы полинома [7] примет вид
R
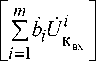
U = ОЕЛ • ак r r = 1
Лаr XCr(k1,k2^,,.)Ш2f -^rVrЬ r=1 ‘2+"* km = r где V = Uк - отсчеты формируемого сигнала, поступающие на вход корректора. вх
Из выражения (4) следует, что в соответствие ему можно поставить некоторый эквивалентный степенной полином:
m
U ак = : ^ 1 d j V , (5)
где d j – некоторый коэффициент степенного полинома, аппроксимирующего результирующую передаточную функцию корректора и нелинейного элемента.
Н к Н ак
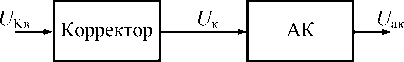
Рис. 4. Схема размещения корректирующего устройства
Fig. 4. Scheme of the correcting device placement
Из (5) видно, что необходимым условием коррекции является соблюдение следующих равенств:
d 1 = 1; d j = 0 при j = 2, ^ m. (6)
Это означает, что в выражении (5) результирующий коэффициент полинома при основной составляющей должен быть равен единице, а значения остальных результирующих коэффициентов должны равняться нулю.
В качестве примера предположим, что порядок полиномов, описывающих передаточные функции корректора и нелинейного элемента, ограничивается пятью. В таком случае, раскрывая в (5) выражения, стоящие под знаками суммы, и приводя подобные, получим:
U ак = a l b l • V +
+ ( a b 2 + a 2 b 2) • V 2 +
+ ( a b 3 + 2 a 2 bb 2 + a 3 b 3) • V 3 + (7)
+ ( a1 b4 + 2 b b3 + bb + з a 3 b 2 b 2 + a 4 bb • V 4 +
2 2 3 55
+ ( «11>5 + 2 a 2( b i b 4 + b 2 Ь з ) + 3 а з (bЬ з + bb 2 ) + 4a4 bb 2 + <1 5 b l ) • V .
Откуда, учитывая (6), т. е. приравнивая коэффициент при основной составляющей к единице, а остальные к нулю, получим, что коэффициенты корректора, с первого по пятый, описываются следующим выражениями:
,
b1 =- a1
b 2 = . ' ( a 2b1 ),
a
b 3 = — • (2 < 2 b i b 2 + 6 3 bl),
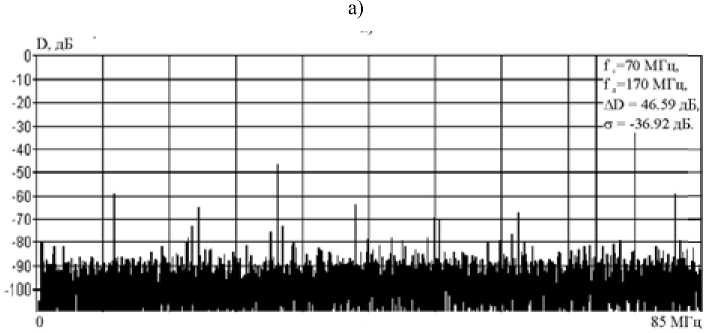
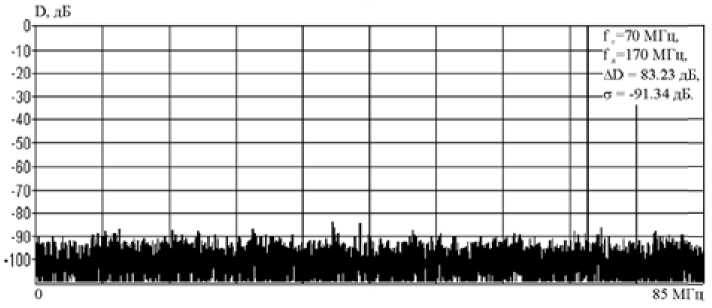
a b4 = — • (2 tl2bib 3 + a 1), =(2 a, b, t). + 2 <<21>21>2 + 3 a1 Из (8) видно, что полученные выражения, начиная со второго, можно объединить следующим рекуррентным соотношением: i)i =-!• mt ,C,k k,. k 2, _, km-D-Kk1 -ixk 2 ‘-j,(9) а)1 =2 12 где Ci (k 1,k2,.,km-i) =------i!полиномиальный коэффициент, при i = 2,m -1. k 1!k 2!. km-1! 1 2 m1 В общем случае, выражение (9) представляет собой бесконечный ряд, однако с практической точки зрения целесообразно брать в рассмотрение ограниченное число членов ряда –m, но не менее чем количество дискретных составляющих в спектре искажений, уровень которых превышает допустимое значение. Таким образом, обобщенная передаточная функция последовательно соединенных корректора и аналогового ключа представляется степенным рядом с новыми, результирующими коэффициентами. Удерживая конечное число членов ряда и учитывая, что условием коррекции является равенство единице результирующего коэффициента при линейном члене ряда и нулю при членах ряда с высшими степенями, получено рекуррентное соотношение для определения коэффициентов корректора. В результате математического моделирования с использованием полученных выражений были рассчитаны спектры и показатели качества формируемых сигналов. Основные результаты моделирования приведены на рис. 5 и 6. Под литерами “а” отображены спектры идеально квантованных сигналов на выходе 10-раз-рядного ЦАП для соотношений синтезируемых и тактовых частот: 0,016 и 0,41. Под литерами “б” отображены спектры синтезируемых сигналов с нелинейными искажениями на выходе АК. Под литерами “в” отображены спектры синтезируемых сигналов с учетом цифровой коррекции нелинейных искажений, возникающих в АК. Анализ результатов моделирования показывает, что предлагаемый метод цифровой коррекции нелинейных искажений достаточно эффективен, так как позволяет сделать следующее: 1. Уменьшить дискретные составляющие спектра нелинейных искажений, тем самым увеличить реальный динамический диапазон ЦФЗС (ΔD), доведя его практически до потенциально достижимого значения, определяемого значением динамического диапазона идеального ЦАП (ΔDэ). 2. Повысить качество синтезируемых сигналов, что выражается в уменьшении среднего квадрата ошибки формирования сигнала (σ) до значения, соизмеримого с уровнем шумов квантования. Предлагаемый метод цифровой коррекции нелинейных искажений предполагает применение корректирующего устройства, размещаемого перед АК, что позволяет увеличить реальный динамический диапазон ЦФЗС и повысить качество синтезируемых сигналов. Метод может быть использован для коррекции нелинейных искажений в ЦФЗС, используемых в радиолокации [8, 9], системах связи и высокоточной измерительной технике. а) б) в) Рис. 5. Спектры сигналов для соотношений синтезируемых и тактовых частот 0,016 Fig.5. Ranges of signals for ratios of synthesizable and clock rates 0,016 Г,-70 МГц, 1,- 170 Ml ц, ,- 87 лБ. б) в) Рис. 6. Спектры сигналов для соотношений синтезируемых и тактовых частот 0,41 Fig. 6. Ranges of signals for ratios of synthesizable and clock rates 0,41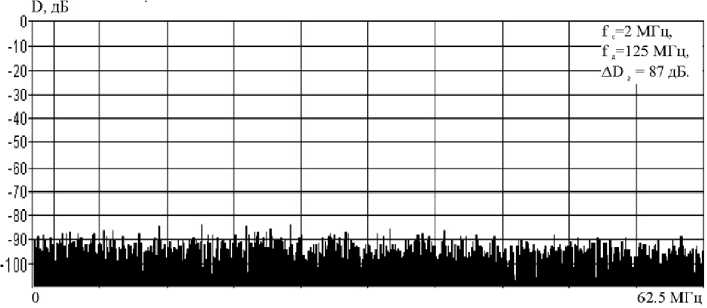
Список литературы Коррекция нелинейных искажений в цифровых формирователях сигналов
- Шапиро Д.Н., Паин А.А. Основы теории синтеза частот. М.: Радио и связь, 1981
- Тирней Дж., Рейдер К.М., Голд Б. Цифровые синтезаторы частот. Зарубежная радиоэлектроника, 1972, 3, 54-74
- Волков Е.А. Математическая модель аналогового ключа и результаты анализа коррекции динамических ошибок цифроаналогового преобразования. Сборник научно-методических материалов, 3(502). Тверь: 2ЦНИИ МО РФ, 2006
- Степаненко И.П. Основы теории транзисторов и транзисторных схем. Изд. 4-е, перераб. и доп. М.: Энергия, 1977. 672
- Богданович Б.М. Нелинейные искажения в приемно-усилительных устройствах. М.: Связь, 1980
- Волков Е.А., Викторов Д.С. Идентификация параметров нелинейной передаточной функции аналогового ключа цифрового формирователя сигналов. Сборник научно-методических материалов XXXIV ВНК. Тверь: ВА ВКО, 2005
- Семендяев К.А., Бронштейн И.Н. Справочник по математике для инженеров и учащихся ВТУЗОВ. М.: Наука, 1980
- Филонов А.А., Васильев О.В., Богданов А.В. Методика построения динамических моделей радиальных скоростей и ускорений пары воздушных целей, летящих в сомкнутом боевом порядке, Известия РАН. ТиСУ. 2007, 4
- Богданов А.В., Васильев О.В., Исаков И.Н., Ситников А.Г., Филонов А.А. Способ сопровождения воздушной цели из класса "самолет с турбореактивным двигателем". Патент на изобретение №2419815, 2009


