Корректирующая способность декодера мягких решений троичных кодов Рида - Маллера второго порядка при большом числе ошибок

Введение. В разнообразных системах передачи и хранения информации для ее защиты от искажений используются алгебраические помехоустойчивые коды [1-3]. Одной из актуальных задач в настоящее время является разработка для

*]

**

Работа выполнена в рамках инициативной НИР.

***

известных кодов новых декодеров, которые обладают какими-либо преимуществами по сравнению с известными декодерами. К таким преимуществам может относиться, например, увеличение скорости работы декодера или повышение корректирующей способности кодека. Так, в последние годы для обеспечения помехоустойчивости актуально применение декодеров мягких решений (ДМР), особенность которых состоит в том, что принятые из канала данные вводятся в декодер, минуя демодулятор [1]. Обычно использование ДМР дает лучшие результаты по сравнению с декодированием жестких решений, когда на вход декодера поступают значения с выхода демодулятора, преобразующего данные из канала в слова над фиксированным конечным алфавитом. Эффективность ДМР основана на том, что в отсутствие демодулятора не накапливаются ошибки квантования, однако обычно декодеры с технологией ДМР обладают большей сложностью — например, [2].

В работе [4] построен мягкий декодер кодов Рида — Маллера второго порядка, заданных над полем Галуа F з (далее RM з(2, т ), т — параметр кода). При этом за основу взят декодер двоичных кодов Рида — Маллера второго порядка В. М. Сидельникова и А. С. Першакова [5], обладающего значительной корректирующей способностью (он исследовался в работах [6-7]). Однако нет теоретической или экспериментальной оценки корректирующей способности нового алгоритма.

Цель данной работы состоит в экспериментальном исследовании корректирующей способности нового мягкого декодера [4] троичных кодов Рида — Маллера второго порядка при различных условиях его эксплуатации. Для достижения цели необходимо решить две задачи. Во -первых, построить модель канала с троичным входом. Источник и приемник сообщений данной модели оперируют цифровыми данными, заданными над полем F з, а линия связи в зависимости от настроек выдает цифровые или непрерывные сигналы над полем комплексных чисел. Во -вторых, провести экспериментальное исследование корректирующей способности нового декодера при различных видах искажений кодовых слов. С этой целью используется программная реализация построенной модели троичного канала связи.

Модель троичного канала передачи данных с использованием канального ДМР -кода Рида — Маллера второго порядка. Рассмотрим элементы модели канала с троичным входом и схему прохождения данных по модели (рис. 1).

Информатика, вычислительная техника и управление

Источник сообщений выдает информационные векторы m=(jnx, т2,...,тк)еРз , где F3 — линейное к-мерное пространство, заданное над полем Галуа F3 .

Затем в кодере канала эти векторы обрабатываются с использованием линейного блочного кода RM з(2, т ) Рида — Маллера второго порядка длины n и размерности к(< п) , заданного над полем F₃ .

Сформированные кодовые векторы с ^F3 поступают в передатчик, который служит интерфейсом к линии связи и преобразует векторы с е F3 в z-kzV Zl^-Fn^'-S )

где С — поле комплексных чисел, сигналы zs, s = \,...,n принадлежат мультипликативной группе корней третьей степени из единицы.

I       J <7=0,1,2

Преобразование аддитивной группы поля F₃ в мультипликативную группу С 3 происходит с помощью естественного изоморфизма ф : F₃ —>С₃, который определяется по формуле фО) = е'^, jeF₃.

Сформированные векторы z = (z_x, z^...^^ передатчик на физическом уровне отправляет в линию связи. Физический аналог сигнала Zj можно получить, например, с помощью модуляции с непрерывной фазой [2]. Диаграмма пространства таких сигналов иллюстрируется рис. 2.

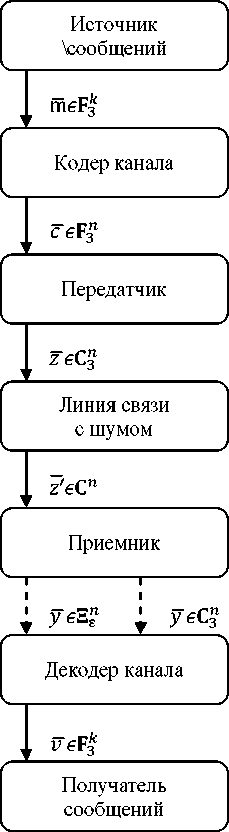
Рис. 1. Схема прохождения данных в моделируемом канале

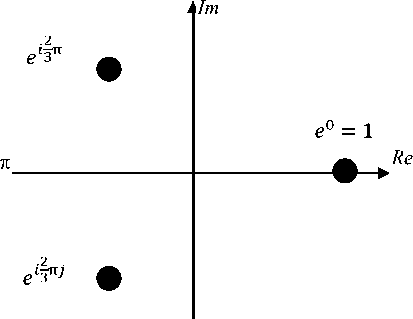
Рис 2. Диаграмма пространства сигналов

В силу искажений, действующих в линии связи, на выходе из нее формируются символы из поля C. Будем рассматривать два базовых вида искажений элементов вектора z е С3 в линии связи — а именно, искажения по фазе и по амплитуде. Под искажением по фазе будем понимать фазовый сдвиг сигнала Zj по единичной окружности. Искажением по амплитуде будет смещение сигнала с единичной окружности по радиу су. Предположим, что под воздействием шума координаты вектора 1 подвергаются различным комбинациям базовых искажений и формируется вектор z'e С”. Графическая иллюстрация искажений сигнала представлена в левой верхней четверти рис. 3. Так, сигнал е* показан черной точкой, голубая точка соответствует его искажению по амплитуде, зеленая — по фазе, а желтая — комбинации двух видов искажения.

Информатика, вычислительная техника и управление

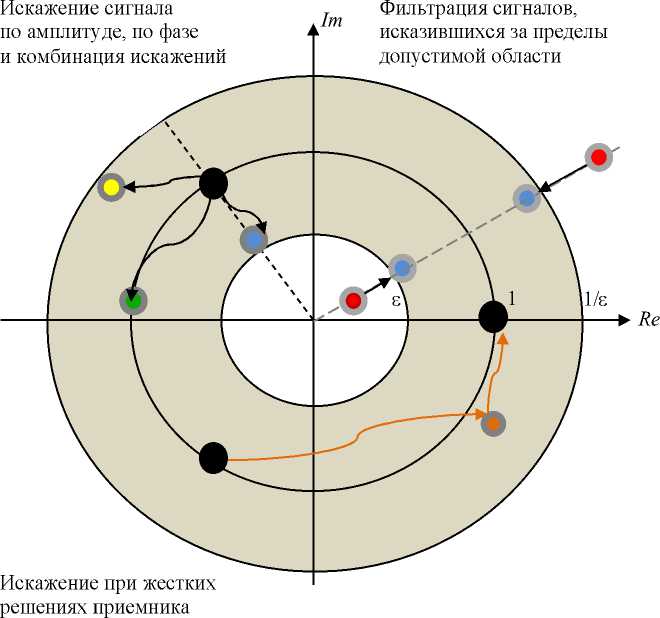
Рис. 3. Примеры искажения сигнала и его фильтрации

Вектор z’ е С” поступает на вход приемника, который в зависимости от настроек может выдавать мягкие или жесткие решения о принятом сигнале. Так, в случае жестких решений приемник преобразует входной вектор z ес в вектор V = (Vb ">.Уп)^е1-з = независимо от типа искажении, поразивших вектор в линии связи. В этом случае может быть использован, например, принцип решающих областей. Таким образом, в результате воздействия

,                                                                                                                                                                                                                                                                   , beF3, а^Ь.В построенной реализации модели такой переход осуществляется равновероятно. На рис. 3 показано, что сигнал с'1 , обозначенный черной точкой, в результате искажения перешел в сигнал, обозначенный коричневой 0

точкой, а приемник с жесткими решениями преобразовал его в сигнал e .

В случае мягких решений приемник фильтрует амплитуду каждого сигнала z_s таким образом, чтобы значения сигнала у_х на выходе приемника принадлежали допустимой области

НЕ=ЬеС|е<Ш<1/е}, где s(e(0;l]) —параметр приемника.

у = (у\, ...,уД ев". Действие фильтра иллюстрируется на правой верхней четверти рис. 3: сигналы, обозначенные красными точками, попавшие в результате искажений в линии связи за пределы допустимой области, переводятся приемником в сигналы, лежащие в области допустимых значений, с помощью смещения их по радиусу к ближайшей точке на границе области S_E. Допустимая область выделена на рис. 3 серым цветом. Используя принятую в теории связи терминологию, можно говорить, что в случае работы приемника в режиме жестких решений реализуется цифровой канал, а в случае работы в режиме мягких решений — полунепрерывный канал.

y ника) направляется в декодер мягких решений, цель которого — восстановить информационный вектор т е F3 , посланный ранее источником сообщений. Результат декодирования v(e/^) поступает получателю сообщения. В зависимости от уровня повреждения вектора Z в канале связи результат декодирования может совпадать с исходным вектором или отличаться от него. Если т — V , то принято говорить о верном декодировании, иначе говорят об ошибке декодирования.

Определение кодов Рида — Маллера RM з (2, m ). Используя [4], [8], определим троичный код Рида — Малл ера RM 3(2, m )

RM3(r, m) { f( 1),..., f( n) | f F3(2)[x1,..., xm]          , где п = 3,й — длина кода, множество г/ а ? I а = (а а и

.

Далее в работе используем следующее упорядочение:

— по целочисленной сумме координат р(ос) вектора а е F” как натуральных чисел от меньшего к большему, а при одинаковых суммах — обычное лексикографическое упорядочение слева направо от большего к меньшему;

m                               .

Степень dcg(/ ) полинома f определяется как максимальная степень составляющих его ненулевых моно-

.

,

г(х) е F^^,..., .x„J, называется информационным вектором. При этом предполагается, что для нумерации элементов информационного вектора, как и кодового, используется упорядочение (1). Кодирование информационного вектора осуществляется путем вычисления значений соответствующего информационного полинома в точках пространства F™ , упорядоченного в соответствии с (1). Способы нахождения числа гарантированно исправляемых ошибок в общем виде см. в [4], [8]. Далее в работе будем использовать уже вычисленные значения.

Конструкция ДМР для кодов RM з (2, m ). На вход алгоритма подаются параметр m кода RM з(2, m), связаиные с m зна- n                        RM 3 (2, m )

Y = (Y .,YB ) еВ^сС), элементы которого занумерованы в соответствии с (1). На выходе алгоритма формируется

.

:, где уД — число, сопряженное YB , векторы у е F™ упорядочены по (1). Далее везде, где нумерация элементов векторов или наборов осуществляется векторными переменными из г^ , по умолчанию будем использовать упорядочение (1).

,

.

^{В =} ^=°^^ВЪ’-’^В1^{>1 и} v4 = (4 =0,4 ..,4 ) В, где В- — вектор

Р = (P₁,...,P_m) е F” , на котором достигается 4 — минимальное значение функционала

МР) = ХМ -^^(e К), где ^Р,а^(е4) — скалярное произведение, ро еК.

Шаг 3. Построим (пхт) -массив ©, строки которого инициализируем значениями из набора B : @(a_s) = В„ = (9_1Ве ,-,Q_mц )eF™. Далее j -й столбец полученного массива будем обозначать ©у , j = 1,..., т . Для каждого a, е F” и всех р_у g F” таких, что р. * a, вычислим

Ж) := МаЖа, + р;) - 0(р;))-      , где функция Maj возвращает элемент, встречающийся наибольшее число раз.

Шаг 4 . Для каждого j = 1,..., т найдем Jy как минимум функционала

, заданного на множестве всех линейных однородных полиномов вида ф(х) = ^^Ф»^ , Фв е У]■ Полином ф, на котором достигается минимум, обозначим ®(;)(х) = ^”1а)^).х? .

Вычислим У(У ⁼Х^<₇^а®^хЛ, где х е F” , а е F₃, q,j е[1,..., т\ , а^ = d_jq и

0)^\если dq < dj

О)^⁰, если d_q³ dj

Шаг 5 . Среди множества векторов С, = t^,...,^ ) е F” и значений ^₀ eF₃ найдем те, которые минимизируют

Информатика, вычислительная техника и управление

O(y.0 = ynJya

X ’        Z—is=\ | ^as

__еФ(<л+^-^с1к^+,1'1л))|(_е р^

где 4’as )(е^з)- скалярное произведение.

Из найденных значений составим полином ф(х) = У^с^,. + с₀ = ^гДе коэффициенты c_k ^F^, k = 0,..., т соответствуют найденным значениям С, и ^₀.

Результат декодирования строим в виде полинома: /(х) = ф(х) + (р(х), который определяет искомый инфор мационный вектор f

Экспериментальное исследование. В работе проведено моделирование передачи закодированной информации по троичному каналу связи как с жесткими, так и с мягкими решениями приемника. Канал связи моделировался с использованием информационной системы «Канал» [9], для которой были созданы специальные библиотеки. При проведении экспериментов параметры модели задавались следующими входными данными:

— значение т, определяющее параметры помехоустойчивого кода RM з(2, т );

— число ошибок t, поражающих кодовое слово;

— тип приемника.

Если использовался приемник с мягкими решениями, то применялись дополнительные настройки, указывающие на вид используемых базовых искажений элементов кодовых слов, а также параметр приемника s, задающий допустимую область значений Se, при использовании искажений по амплитуде. Проведено 104 испытаний для каждого набора параметров модели.

Отметим, что при моделировании потоков ошибок часто используется понятие пораженных символов, т. е. попавших под воздействие искажений, но по случайности не изменивших своего значения [3], [10]. При проведении экспериментов такая ситуация намеренно не моделировалась, т. е. в результате наложения t ошибок на кодовое слово это слово отличалось от исходного ровно в t позициях.

В табл. 1 описаны основные параметры кодов RM 3(2, m), результаты экспериментального исследования которых представлены ниже. В этой таблице использованы следующие обозначения: m — параметр кода RM 3(2, m ); n , k и t — длина, размерность кода и число гарантированно исправляемых ошибок (определяемое по минимальному расстоянию кода). Отношение t / n задает максимальное значение вероятности ошибки в канале связи, при котором код «гарантирует» выдачу верного результата. Отметим, что при ошибках, вероятность которых превышает t / n, классический детерминированный декодер всегда выдает ошибочные результаты. Параметр t / n показывает избыточность кода. При необходимости далее будем использовать традиционную краткую запись параметров кода в форме тройки [ n , k , d ], где d — минимальное кодовое расстояние.

Таблица 1

Основные параметры кодов RM 3(2, m ), m =2, 3, 4, 5

m	n	k	t	t/n	n/k
2	9	6	1	0,111	1,5
3	27	10	4	0,148	2,7
4	81	15	13	0,160	5,4
5	243	21	40	0,164	11,57
6	729	28	121	0,165	26,03

Проведенная серия экспериментов по определению корректирующей способности нового ДМР -кода RM 3(2, m ) в случае применения его в канале с жесткими решениями приемника показала значительное повышение числа исправляемых ошибок по сравнению с детерминированным декодером. Изменение значения максимальной вероятности исправляемых ошибок новым декодером по сравнению с детерминированным декодером представлено в табл. 2. В верхней строке таблицы указаны максимальные вероятности ошибок, исправление которых гарантируется кодом (параметр t / n , см. табл. 1). Вторая строка таблицы содержит максимальные вероятности ошибок, при которых новый мягкий декодер выдал верный результат во всех проведенных экспериментах (т. е. в 100 % случаев). Из приведенных результатов видно, что декодер значительно улучшил результат, гарантированный кодом, во всех случаях, кроме кода RM 3(2,2). Так для RM 3(2,3) корректирующая способность увеличилась на 34 %, для RM 3(2,4) — на 54 %, а для RM 3(2,5) — на 157 % (код гарантирует исправление 40 ошибок на кодовое слово, а декодер во всех проведенных экспериментах исправил все ошибки до 103 включительно на кодовое слово). Третья и четвертая строки таблицы отличаются от второй вероятностью выдачи декодером верного результата (третья строка — верный результат в 95 % случаев, четвертая — в 90 % случаев).

Таблица 2

Корректирующая способность нового декодера кода RM 3(2, т )

в случае применения его в канале с жесткими решениями приемника

Максимальное значение вероятности исправляемых ошибок, гарантируемое	Параметр кода RM 3(2, m )
	m = 2	m = 3	m = 4	m = 5
КОДОМ RM 3(2, m )	0,111	0,11	0,160	0,165
декодером с вероятностью 1	0,111	0,148	0,247	0,424
декодером с вероятностью 0,95	0,111	0,185	0,321	0,428
декодером с вероятностью 0,9	0,111	0,185	0,333	0,436

Для определения чувствительности нового ДМР -кода RM 3(2, m ) к различным базовым типам искажений и их комбинациям проведена серия экспериментов с различными настройками параметров модели канала связи. На рис. 4 представлен график зависимости вероятности верного декодирования от вероятности ошибки в канале связи для кода RM 3(2,4).

Рассмотрим график подробнее. Кривая с подписью «Дискретные ошибки» отражает результаты экспериментов, проведенных в канале связи с жесткими решениями приемника. Напомним, что в этом случае ошибка переводит сигнал в один из двух других разрешенных сигналов из поля C3. Кривая с подписью «Ошибки по фазе» отражает результаты экспериментов, проведенных в канале связи, где происходят только ошибки типа сдвига сигнала по фазе. Кривые с подписью «По фазе и амплитуде» отражают результаты экспериментов, проведенных в канале связи, где происходят различные комбинации ошибок по фазе и по амплитуде, в скобках указан параметр приемника е , опреде- ляющий ширину допустимой области SE. Легко видеть, что чем меньше значение 8, тем область НЕ больше. Эксперименты показали, что чем шире область допустимых значений (т. е. чем значения 8 меньше), тем хуже корректирующая способность декодера. Однако для каждого кода находится такое значение 8, при увеличении которого значительного изменения корректирующей способности практически не происходит. Так для кода RMз(2,4) результаты экспериментов при значениях 8 е [0.5,1] практически неразличимы. На графике не представлена зависимость корректирующей способности декодера в случае, когда происходят только ошибки по амплитуде. Эксперименты показали, что декодер не чувствителен к таким ошибкам, если не происходит сдвига сигнала по фазе. Так, для числа ошибок типа по амплитуде от 1 до длины И кода декодер всегда выдает верный результат. Отметим, что взаимное положение кривых, представленных на графике, повторяется для различных кодов RMз(2,m), т > 2.

Информатика, вычислительная техника и управление

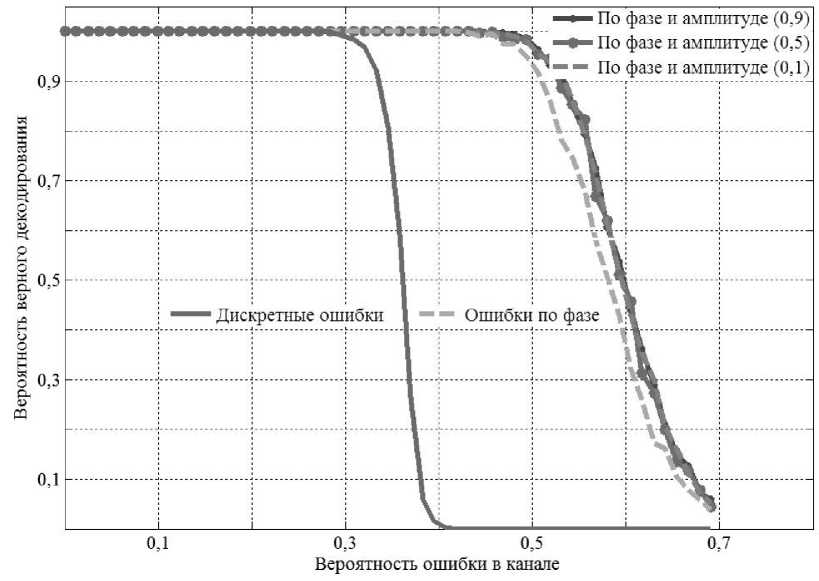
Рис. 4. Результаты исследования [81, 15, 27]-кода RM з(2,4)

В работе проведена серия экспериментов по поиску зависимости корректирующей способности декодера от расположения ошибок внутри кодового слова. Результаты экспериментов показали, что декодер не чувствителен к местоположению ошибок.

Из табл. 1 видно, что [243, 21, 81]-код RMз(2,5) обладает достаточно высокой избыточностью n/k = 11,6. Возникает очевидный вопрос: целесообразно ли использовать этот код с его трудоемким алгоритмом декодирования или имеет смысл использовать коды с большой избыточностью и простыми декодерами? Рассмотрим в качестве кода, имеющего хорошую корректирующую способность и простой алгоритм мажоритарного декодирования, код повторения [1], [11] с близким значением избыточности и сравним корректирующие способности кода RMз(2,5) и [11,1,111-кода многократного повторения над алфавитом Fз, который гарантированно исправляет 5 ошибок на 1 кодовое слово и обладает избыточностью, равной 11. Для того, чтобы сравнять длины кодовых слов обоих кодов, объединим 22 кодовых слова кода повторения — например, с помощью техники прямой суммы кодов [1], [И]. Таким образом, длина составного кодового слова — 242 символа, и код может гарантировано исправить 110 символов в этом составном слове, но только при жестком ограничении: ошибочные символы должны быть распределены внутри кодового слова равномерно (не более 5 ошибок на 11 -символьный отрезок кодового слова). Код Рида — Маллера может гарантированно исправить только 40 ошибок внутри кодового слова длиной 234 символа, однако результат его работы не зависит от местоположения ошибок. Если использовать новый мягкий декодер кодов Рида — Маллера, то в рассматриваемом случае можно будет исправить 103 ошибки, также независимо от места их положения. Более того, если применять новый декодер в полунепрерывном канале связи, то декодер сможет исправить не менее 150 ошибок, вне зависимости от места их положения внутри кодового слова. Декодер кода многократного повторения не предназначен для исполь- зования в полунепрерывном канале связи. Очевидно, что код многократного повторения, который обычно рассматривают как код, обладающий большой корректирующей способностью, уступает по этому параметру коду RM3(2,5), хотя, очевидно, выигрывает по скорости работы алгоритмов кодирования и декодирования. Для кодов RM3(2,m) с другими значениями параметра m аналогичные рассуждения также показывают выигрыш в корректирующей способности по сравнению с кодом многократного повторения. При этом с ростом m данный выигрыш растет, а с уменьшение значения m — падает.

Заключение. Результаты проведенных экспериментов показали, что исследуемый декодер троичного кода Рида — Маллера второго порядка обладает значительной корректирующей способностью по сравнению с классическими детерминированными декодерами — например, с декодированием по минимуму расстояния Хэмминга. Новый декодер мягких решений может быть применен для обеспечения помехоустойчивости в каналах связи низкого качества, используемых, однако, для передачи ценных сообщений. Так, на графике 4 видно, что даже при вероятности ошибки в канале связи, равной 0,5, т. е. значению, при котором говорят о разрыве линии связи, декодер выдает верные результаты с высокой достоверностью. Кроме традиционного применения декодера для обеспечения помехоустойчивости он может быть использован в таких практических приложениях, как восстановление информации, полученной по побочным (отводным) каналам связи [12], при построении криптосистем типа Мак-Элиса и Ниддерайтера [11].