Корреляционная обработка кубоида инфракрасных изображений, получаемых с беспилотных летательных аппаратов. Часть 1. Моделирование и обработка инфракрасных сигнатур техногенных объектов в процессе суточного изменения температур
Автор: Ищук И.Н., Громов Ю.Ю., Постнов К.В., Степанов Е.А., Тяпкин В.Н.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 3 т.9, 2016 года.
Бесплатный доступ
В статье рассматривается технология формирования и корреляционной обработки кубоида ИК-изображений техногенных объектов в ходе суточных наблюдений. Представлена общая постановка задачи нестационарного теплообмена в прямоугольной области анизотропного в отношении теплопроводности материала, аппроксимирующего техногенный объект. Приведены результаты обработки корреляционным алгоритмом динамических ИК-сигнатур, полученных в результате численного моделирования.
Тепловая томограмма, тепловое излучение, тепловой контраст, динамические ик-сигнатуры, теплопроводность материалов, термодинамическая температура, кубоид ик-изображения, тепловой обмен, скрытые объекты
Короткий адрес: https://sciup.org/146115065
IDR: 146115065 | УДК: 518.6, | DOI: 10.17516/1999-494X-2016-9-3-310-318
Текст научной статьи Корреляционная обработка кубоида инфракрасных изображений, получаемых с беспилотных летательных аппаратов. Часть 1. Моделирование и обработка инфракрасных сигнатур техногенных объектов в процессе суточного изменения температур
Рис. 1. Схема определения теплофизических параметров техногенных объектов: 1 – БЛА квадрокоптерного типа с тепловизором на борту; 2 – станция управления БЛА; 3 – модель техногенного объекта (техники) и эталонных материалов; 4 – термометр; 5 – мобильная метеостанция
С другой стороны, данные практических исследований дистанционного измерения температур, начатых с середины прошлого века, в начале в ИК-диапазоне длин волн, а затем и в радиодиапазоне показывают, что величины тепловых контрастов в большей степени определяются теплофизическими параметрами материалов, из которых изготовлены объекты, их размерами, свойствами подстилающей поверхности и метеорологическими условиями [3-6]. На рис. 1 приведена схема проведения дистанционных измерений теплофизических параметров техногенных объектов путем получения их ИК-сигнатур. Съемка экспозиции техногенного объекта производится с заданной периодичностью в течение суток, что позволяет сформировать кубоид ИК-изображений [1, 2].
На основании этого исследование закономерностей динамического изменения тепловых контрастов (температурных контрастов) материалов, связанных с практически не изменяющимися теплофизическими параметрами объектов и фонов, является актуальной задачей. Решение указанной задачи позволяет в ходе дистанционной оценки теплофизических параметров характеризовать все объекты по своим, присущим только им, параметрам с проведением их типизации [7].
Постановка задачи
Рассмотрим процесс нестационарного теплообмена в прямоугольной области анизотропного в отношении теплопроводности материала. Если в условиях однозначности решения в качестве граничных условий рассматривать условия первого рода, то математическая модель этого процесса имеет вид следующей краевой задачи:
C(Т) — = — | ^ .(Т) — | + — I ^2(Т) — \ + 2 — I ^2(T) ~\ + S(x,УT), (1) дт ax I axJI j dxI j где x e[0, a];y e[0, b ];те[0,Тт ] - координаты и время, C = р • c ; р - плотность; с - теплоемкость; T- температура; Хц(Т), ^22(T), ^12(T) — компоненты тензора теплопроводности;
Т ( x , y ,0) = ^ o ( x , y ),
T ( x r , У г ,т ) = Ф г ( x r , У г ,т ), x r = { 0; a } , y r = { 0; b } , r e [ 0, r m ] (3)
где ф 0 ( x , y ), фг ( xr , yr, т ) и S ( x , y , т ) - известные функции начального распределения поля температур, граничных условий и функции объемного источника тепла.
Теплофизические параметры зададим в виде функции ^ ^( Т ), ^ 2( Т ), ^ 2( Т ) и C ( Т ), зависящих от мгновенных значениях температур в определенных n точках прямоугольной области G = [0; а ] х [0; b ] , при T ( x i , y i, т ) = f ( x i , yt, т ), i =1,2,..., n и известных функциях S ( x , y , т), Ф 0( x y ), Ф Г ( x r , У г , т Г )
Для упрощения теплофизические параметры Я ц( Т ), Я 22 Т ), ^ 12 ( T ) и C ( Т ) зададим в параметризованном виде:
m + 3 m + 3 m + 3
MT) = S Я(1Lk(T), Я22(Т) = S 4?Lk(T), Я12(Т) = S Я(2Lk(T), k=1 =1 k=1
C (T ) = m + 3 C ( k ) Lk ( T ) k = 1
где Lk ( T ) - последовательность интерполяционных полиномов Лагранжа; Т e [ T min, T max ] m – число участков разбиения области определения функций при осуществлении их ™н- ( k ). ,,<—„,,„; Л ,, = k U ,1 , k - 1,2 ^ ,( m + 3», X 22 = ( Л 22 , k = 1,2 ^ ,( m + ЗД,
X 12 = ( x 12 , k = 1 , 2 - , ( m + 3)) , C = ( C ' kk = 1 , 2 ^ , ( m + 3)) - векторы значений параметров интерполяционных полиномов.
Кроме того, упростим
5Г d t \df d t A_,m82 t ^d(TT ) f5 t
I X ( T )-— l + I Л ( У )—1 = Л ( T )— +I I + 8 x I 8 x ) 8 y ( 5 y J 8x 8T 15 x J
62 T 8Л( T ) (8 T ) 2 (82 T 82 T ) 8A(T ) n
■ .. . = ^ ( T )i - ■ - при ^^«0
8y 8T<8y J (5 x 8 y J
Численную оценку параметров техногенного объекта будем производить путем нахождения максимумов коэффициента взаимной корреляции между данными дистанционно-измеренных динамических значений температур и рассчитанных на основе соответствующей математической модели «эталонного» материала. В [8] аналогичный подход рассматривается в качестве метода распознавания образов, известного как корреляционное сопоставление поиска эквивалентов объекта-эталона, представленного в виде вектора, матрицы или массива. Расчет коэффициента взаимной корреляции будем производить по всему растру кубоида ИК-изображений в соответствии с выражением
K
, Е ( Ф [ k ] p-q. -ф [ k ] p ,. q -) . ( Ф [ k ] p,q -ф [ k ] p, )
J p,q
1 . k zT
K CT * * ■ CT p, q p, q
где p e 0, P , q e 0, Q , k e 0, K , где P^Q - растр кубоида ИК-изображений, Ф - математическое * *
ожидание яркости, о - среднеквадратичное отклонение яркости, p, q - координаты отсчетов эталонов, К – количество отсчетов во времени, Ф – относительное значение яркости Ф∈ [0;1] , которое получают из системы уравнений
f Tr = sT 4 + (1 - s) T4;
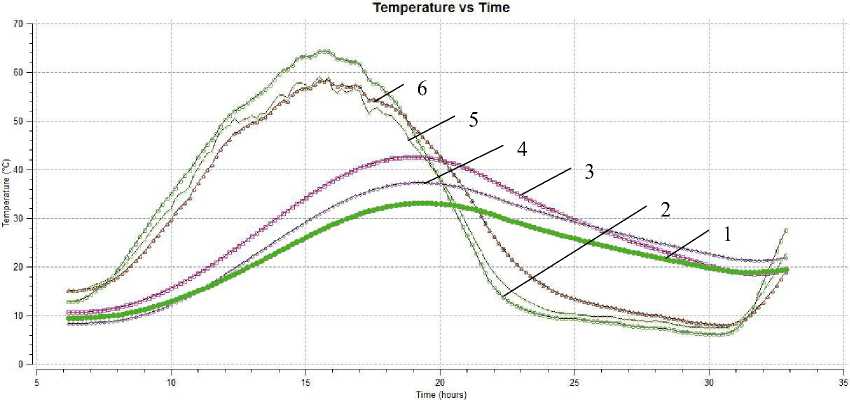
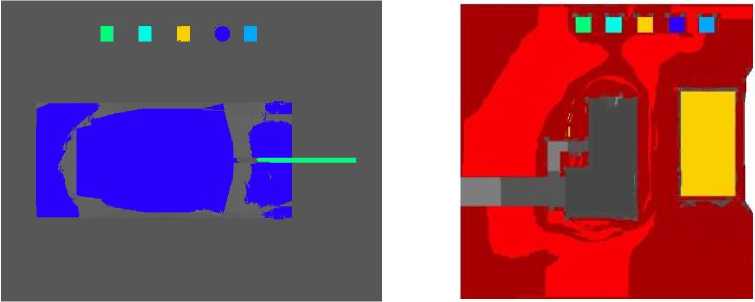
|г = Ф(Т -T ) + T J На основании численного решения прямой задачи (1) - (4) задачу сегментации кубоида ИК-изображений сформулируем следующим образом. На каждой итерации оценки J по 5-эталонам рассматриваемый пиксел кубоида ИК-изображений добавляется в соответствующий сегмент, для которого J имеет значение больше заданного порога. В противном случае пиксель считается сильно отличающимся от всех текущих областей и создаётся новая область – область неопределенности. Описание модели С использованием среды трехмерного теплового моделирования на основании (1) – (3) были построены модели техногенных объектов (объект техники, здание и бункер) и эталонных материалов, покрытых черной краской, на фоне антропогенных ландшафтов (рис. 2). В ходе проведения численного моделирования динамики изменения возникающих радиационных контрастов в среде теплового моделирования были использованы данные метеорологических наблюдений погоды, зафиксированные в интервале времени с 06:10 до 08:50 следующих суток в точке с координатами 51.61 с.ш. 39.137 в.д. на высоте 98 м над уровнем моря. Результаты расчетов суточного изменения термодинамических температур наблюдаемых на поверхностях объектов и материалов представлены на рис. 3. В ходе численного моделирования в соответствии со схемой определения теплофизических параметров (рис. 1) было получено по 27 ИК-сигнатур исследуемых техногенных объектов с интервалом в 1 ч, некоторые из них изображены на рис. 4. Алгоритм сегментации изображения Для сегментации кубоида ИК-изображений и выделения областей по схожим параметрами обработку полученных данных необходимо производить в соответствии со следующим алгоритмом: Шаг 1. Считывание динамических ИК-изображений и формирование кубоида ИК-изображений [1]. Задание координат центра эталонных объектов и формирование векторов динамических значений изменения яркости Ф , ,. p, q _ Шаг 2. Расчет векторов численных значений математического ожидания Φ и p, q СКО о * * изменения яркости на интервале времени наблюдения для каждого эталонного материала. Шаг 3. Расчет коэффициента корреляции между каждым пикселем растра кубоида ИК-изображений и вектором динамических значений изменения яркостей эталонных объектов Ф * * с формированием массива невязок JPQ в соответствии с выражением (4). p, q б) Рис. 2. Тепловая модель техногенных объектов: а – объект техники; б – здание и бункер. Обозначения и параметры материалов: 1 – объект исследования (техника, скрытый объект); 2 – плита из пенопласта (λ= 0,04 Вт/м∙К, c= 1400 Дж/кг∙К); 3 – стальной лист (λ= 58 Вт/м∙К, c= 482 Дж/кг∙К); 4 – бетонная плита (λ= 1,28 Вт/м∙К, c= 880 Дж/кг∙К); 5 – деревянная плита (сосна) (λ=0,18 Вт/м∙К, c=2300 Дж/кг∙К); 6 – плита из красного полнотелого кирпича (λ= 0,67 Вт/м∙К, c= 860 Дж/кг∙К) Рис. 3. Графики изменения термодинамических температур: 1 – исследуемый объект; 2 – плита из пенопласта; 3 – стальной лист; 4 – бетонная плита; 5 – деревянная плита (сосна); 6 – плита из красного полнотелого кирпича а) б) Рис. 4. ИК-сигнатуры техногенных объектов: а – объект техники; б – здание и бункер Шаг 4. Выбор оптимального по критерию Неймана – Пирсона порогового значения невязки HJ для проведения сегментации кубоида ИК-изображений по заданным эталонным материалам. Шаг 5. Построение сегментированного изображения в цветовой модели HLS. В результате применения разработанного алгоритма корреляционной обработки кубоида ИК-изображений были получены сегментированные изображения техногенных объектов, представленные на рис. 5. Анализ полученных тепловых томограмм показывает, что предложенный корреляционный алгоритм позволяет выделить в пределах растра ИК-изображения элементы конструкционных и функциональных материалов, из которых состоит техногенный объект, по сходству их теплофизических параметров эталонным материалам. Так, на рис. 5 – 316 – а) б) Рис. 5. Сегментированные изображения техногенных объектов: а – объект техники; б – дом и бункер на фоне местных предметов отчетливо выделен объект «техника», корпус которого отнесен к материалу «стальной лист», а малозаметный объект «бункер» отнесен к материалу «бетонная плита», несмотря на то что он покрыт слоем грунта. Выводы Таким образом, в статье представлен алгоритм корреляционной обработки кубоида ИК-изображений в задачах автоматического обнаружения объектов по их теплофизическим параметрам на примере сегментации изображений техногенных объектов, полученных в ходе численного моделирования динамики изменения термодинамических температур на поверхностях исследуемых и эталонных материалов. Для оценки качества работы алгоритма проводилась попиксельная обработка ИК-сигнатур объектов с вычислением невязки и выбором по критерию Неймана – Пирсона пороговых значений невязок, обеспечивающих сегментацию изображений по заданным эталонным материалам. Представленные результаты показали преимущество корреляционной обработки по сравнению с подходом, описанным в работе [9]. Работа выполнена при финансовой поддержке РФФИ (грант № 15-08-02611 А).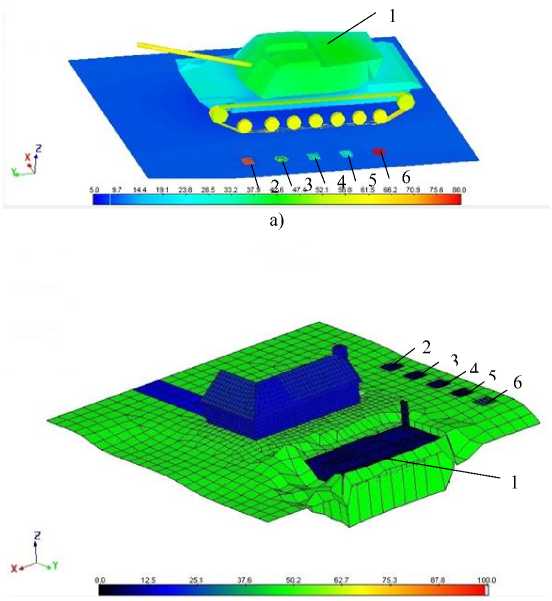


Список литературы Корреляционная обработка кубоида инфракрасных изображений, получаемых с беспилотных летательных аппаратов. Часть 1. Моделирование и обработка инфракрасных сигнатур техногенных объектов в процессе суточного изменения температур
- Ищук И.Н., Парфирьев А.В. Измерительная техника, 2014, 10(56), 1162-1166
- Ищук И.Н., Парфирьев А.В. Измерительная техника, 2014, 1(57), 74-78
- Yong Xu, Xiangyu Wei, Ge Wang. International Journal of Biomedical Imaging, 2009, Special section, 1-4.
- El Hazzat, Soulaiman Saaidi, Abderrahim Karam, Antoine Satori, Khalid. 3D Research. 2015, 6, 1-18.
- Ishchuk, I.N., Filimonov, A.M., Tyapkin V.N., Semenov M.E., Kabulova E.G. Modern applied science, 2015, 2, 206-215.
- Ishchuk, I.N., Parfiriev, A.V, Tyapkin V.N., Semenov M.E., Kabulova E.G. Modern applied science, 2015, 3, 233-241.
- Khutorskoi M.D., Podgornykh L.V. Reports on Earth Sciences, 2006, 2, 225-229.
- Buchnev A.A., Tyapkin V.P. Journal of Siberian Federal University. Engineering & Technologies, 2015, 6(8), 701-705.
- Громов Ю.Ю., Губсков Ю.А., Ищук И.Н., Ворсин И.В. Промышленные АСУ и контроллеры, 2014, 6, 24-28


