Корреляционная обработка кубоида инфракрасных изображений, получаемых с беспилотных летательных аппаратов. Часть 2. Метод обработки инфракрасных сигнатур эталонных объектов на основе численного решения нелинейной задачи теплообмена

В последние годы как в России, так и в других странах мира в практику дистанционного зондирования Земли всё более ускоряющимися темпами внедряются технологии многоспектральной съемки. Данный вид съемки представляет собой новое перспективное направление исследования объектов поверхности Земли посредством изучения свойств объектов на основе анализа информации о распределении отраженного от них излучения в зависимости от длины волны. Многоспектральная съемка реализует для заданного района местности одновременное получение десятков и сотен изображений одной и той же сцены, зафиксированных в видимом и инфракрасном диапазонах длин волн в различные промежутки времени. При многоспектральной съемке наиболее значимыми являются данные, полученные в инфракрасном (ИК) диапазоне длин волн, так как информация о температурах объектов, расположенных на поверхности Земли, позволяет дистанционно определять их теплофизические свойства. Однако данная задача требует построения сложной математической модели процессов теплообмена, а также учета всего многообразия факторов, влияющих на процесс формирования радиационных температур и определяющих климат на поверхности Земли. Следовательно, можно сделать вывод об актуальности и целесообразности разработки принципиально новых программно-математических методов об- работки и анализа информации, полученной в ИК-диапазоне длин волн, для определения теплофизических свойств дистанционно исследуемых объектов, а также их дальнейшей сегментации и идентификации.

Постановка задачи

Реализация метода анализа ИК-сигнатур, полученных при многоспектральной съемке объектов, расположенных на поверхности Земли, для определения их теплофизических параметров с учетом процессов теплопередачи в них состоит из трех этапов [1]. Первый этап - решение прямой задачи теплопроводности, математическая модель которой представлена дифференциальным уравнением теплопроводности с граничными и начальны -ми условиями. Следующим этапом является решение коэффициентной обратной задачи (КОЗТ) с составлением и минимизацией функционала невязки по рассчитанным и экс -периментально измеренными значениям температур на исследуемой поверхности. По результатам решения КОЗТ строится пространственное распределение теплофизических параметров (ТФП) – томограмма. Третий этап – решение задачи обнаружения объектов по томограмме.

Наиболее важный из этих этапов - этап постановки прямой задачи теплопроводности, который должен максимально учитывать все процессы, влияющие на формирование теплового поля в исследуемой среде. Для построения математической модели теплового поля многослойного изотропного материала рассмотрим двумерное дифференциальное уравнение теплопроводности, которое удобно применять к телам цилиндрической формы (рис. 1).

Математическая модель

Постановка прямой задачи теплопроводности для многослойной среды для двумерного случая с учетом граничных условий теплового баланса земной поверхности и сопряжения, учитывающего неидеальность теплового контакта соприкасающихся поверхностей [2], выглядит следующим образом:

4 (т )

=0

5 Т

I z— 0

I z=-h1    RT д Т1

Т2| z-H-Тср. с где р * - плотность материала, кг^м-3; с * - удельная теплоемкость материала, Дж-кг-1*К-1; Т - избыточная температура, К; т - время, c; X - теплопроводность, Вт*м-1-К-1; ср - удельная изобарная теплоемкость воздуха, Дж-кг-1*К-1; р - плотность воздуха, кгм"3; к - коэффициент турбулентности в приземном слое атмосферы, м2^с; 9 - потенциальная температура, K, 5 - массовая доля водяного пара, %, z - вертикальная координата в глубину, м; x –координата в ширину, м; L – удельная теплота парообразования, Дж∙кг;

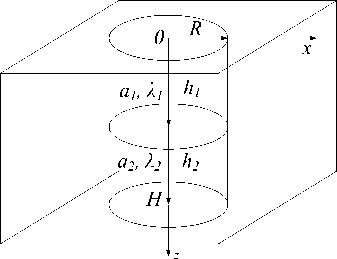
Рис. 1. Схема распространения тепла в цилиндрических телах

B*_o=3 TT^ - a_aTT4 - эффективное излучение поверхности первого слоя, Вт^м^-2; 5 - поглощательная способность поверхности первого слоя; а ^- постоянная Стефана - Больцмана, Вгм 2X4 q ^- плотность теплового потока, В™—^{2; r}t ^- коэффициент термического сопротивления, м²-К-Вт-1; H - координата нижней границы многослойного материала; T ср.с – среднесуточная температура воздуха, К.

Разностный аналог выражения (1) представляется в следующем виде [3, 4]:

Т к +1 _ jk               тк +1 _ утк +1 , у к +1

T pn--- T pn ₌ гу ^{к    1 p}-'ⁿ 2 ^{1 pn 1 p} ■"

^_т       a i [² p , n ]             д z 2

Тк +1 _ утк +1 , ук +1

к     T p ^, n +1    T^p p ^, n ^T1p ^, n -1 -io.

+ a I T p , n J--д Х--------’ i - V’

, т^к -T^k л ,       , ЛАТ^к 1-A

_ ; vt^k i T p ^{, n} T p ^{+1, n} _zy т^к —__n^kT ^{L1[ 1}p ^{, n J 1L p , n J}     A z         ■ n"" ^{q      2} aLT кn J

Tк +1 _ ук

Tp , n Tp +1, n ,

At ^;

^1 L T p , n J

T n

Tk _Tk Tk _ Tk

I T i n n Tp +1, n Tp +1, n Tp -1, n.

----A z----⁼-----v-----’

2 ¹• n ^J _{t       +}     ^* ^ " ^J к

ДГГ ^к НЯЛТ'¹ ] '⁴ⁿ  Я,[Т^к ] + Я,[Г ^к ]

1 p , n          2 p , n                      1 p , n          2 p , n

_Tk ¹ p^ 1, n

• v ;

k

H," ср. с, где TkPnn - сеточная функция; к - номер отсчета по времени, к е [0, K]; p - номер отсчета в глубину, p е [0,H]; n - номер отсчета по горизонтали, n е [0,R]; a - коэффициент температуропроводности слоя, м2-с-1; а - коэффициент теплоотдачи поверхности, Вт-м"2-К"1; д - номер отсчета, соответствующий границе сопряжения в многослойной среде; Ат - величина шага дискретизации по времени, c; Δz – величина шага дискретизации по пространству в глубину слоя, м; Δx – величина шага дискретизации по ширине, м; v – коэффициент тепловых потерь.

k

qk

kk

1 2/ exp           exp

В \          В

1/             ^1

Р 1

E , ^к<К *;

( к-К >Ат-2/ exp

V                     ' 2

exp

( к-К >Аг

Р ₂

E , к>К *;

где K^* – номер отсчетов по времени, соответствующий времени действия теплового потока; β 1 , β 2 – параметры релаксации теплового потока на стадии нагрева и остывания соответственно, c "1 ; E - энергетическая светимость ИК-излучателя, Вт-м^-2.

Метод решения и исходные данные

Рассмотрим алгоритм расчета нестационарного теплового поля согласно (2) с использованием продольно-поперечной схемы и метода прогонки [5, 6]:

Шаг 1. Задание исходных данных, а также начальных и граничных условий, необходимых для расчета: k , a 1 , a₂ , a, h 1 , h₂ , Ат, T imp , A z , x , в ₁, в 2 , E , ^ 1 , ^ 2 , R , v, Т ср.с , H = h 1 + h₂ . Задание граничных и начальных условий: T ₀( z , x ) и Т Г ( z_r , х_Г , т).

Шаг 2. Введение нелинейности теплофизических параметров. Аппроксимация теплофизических параметров исследуемых материалов кусочно-линейными функциями

А+^Р i , Tkn

PT Tk n > U T i T, n <Ъ  , i £1,2;

k

PT1!* Pi, Tp, n > T2 , где T1, T2 - пороговые значения температур, при которых происходят изменения теплофизических параметров материалов; п — параметры зависимости теплофизических свойств от изменения температуры; ρ – теплофизические параметры исследуемых материалов.

Шаг 3. Вычисление плотности теплового потока q^k согласно (3).

Шаг 4. Последовательное прохождение временных отсчетов по k от 0 до K c шагом Δτ.

Шаг 4.1. Прогонка пространственных отсчетов по n от - R до R c шагом A x .

Шаг 4.2. Прогонка по глубине p от 0 до H с шагом Δ z при целом временном шаге.

Шаг 4.2.1. Вычисление вспомогательных коэффициентов a k,p , b k,p , c k,p , d k,p для p € [ 0,^ ] :

a TkA^    2-a TT^    a TT^к

1      p,n                                      1 p,n                                   1 p,nk ak,p        V! ; b k,p           TA          1; c k,p        TA ; dk,p   Tp-1, n • zzz

Шаг 4.2.2. Вычисление вспомогательных коэффициентов a _k , _p , b _k , _p , c _k , _p , d _k , _p на границе сопряжения двух сред (ph).

a 2 №J^Ar к    2- a 2 ft , ].Дг        a ₂ T „ ]-Аг

—НЧ—; b k,p =--4V--1; c k,p = —TA —;

Az                Az                 zz d k, p=(-T

A [ T p^k , n

A T n ]₊A T n]

m k —1

" T P" A ⁿ

A [ T pk , „

A J_+Л ТД

rp k —1 '^Tp +¹, n

. rp k -1

^; Tp , ⁿ -^{d k} , p •

Шаг 4.2.3. Вычисление вспомогательных коэффициентов a _k , _p , b _k , _p , c _k , _p , d _k , _p для p € [ h ₁, H ] :

^a k,p

a2 [Tpknh\ h _  2-a2 [Tpk,„]'Аг a 2 [Tpk, nP^  .     ?k_ 1

A z²       ’ d ^^p"^p- ¹ " •

A _ 2         ^{; b} k,^p              A _ 2             ¹

zz

Шаг 4.2.4. Вычисление прогоночных коэффициентов ek,p, fk,p c k p в граничных точках при p = 0: еk,p = -^p k,p

d k, p к ; b k, p

тт J?

при p = №. ^f k , p =

^d k , p a k , p - 1 ' ^f k , p - 1 ^b k , p a k , p - 1 * ^e k , p - 1

k , p                               k , p       k , p -1 k , p -1

в интервале p e(0, H ): ek,p = ----------------; fk,p =---------------- b k, p - a k, p-1 •e k, p-1             b k, p - a k, p-1 •e k, p-1

Шаг 4.2.5. Определение значений температур на целом временном слое обратной прогон-к-1                                                                k                         к кой при p - H: Tp,n = dk,p; при p e (H,0] с шагом Az: Tp-1,n -tk,z - ek,z • Tp,n.

Шаг 4.3. Организация прогонки на временном полушаге вдоль оси x .

Шаг 4.4. Прогонка по глубине по p от 0 до h₂ с шагом A z при временном полушаге с условиями:

, к Ц a 1 ^ \р ^ [0 А Л _; л A fc\р е [ОЛИ ^рЛ [ a 2 Tp. ] р е^Н\’     pn^ [Z2^] р е^Н'

Шаг 4.5. Прогонка по ширине по n от - R до R с шагом A x при временном полушаге .

Шаг 4.5.1. Вычисление вспомогательных коэффициентов a k _n , b _k , _n , c _k , _n , d _k , _n для n e [ - R , R ] :

_ a [ П,       _ 2-a [ T^. >      a [ T^. > k-1

; к, П       T p , n - 1 .

akn       Л 2      ; b kn           Л 2         1 ; c knд

Ax                Ax

Шаг 4.5.2. Вычисление прогоночных коэффициентов e _k , _n f _kn :

при n = - R : e _kn = —— ; f _k = ^ ; при n - R : f , = ^--- ^{kn 1 k}-n-^{1 b k} , n             ^{b k} , n                                ^{b k} , n ^{- a k} , n ^-i •^{e k} , n ^-i

              c                  d - a• f приn e(-R,R): ek, n                        ; k, n.

• b , — a, , • e, , b, —a, . -e, .

• k , n       k , n -1 k , n -1                    k , n       k , n -1 k , n -1

Шаг 4.5.3. Определение значений температур на временном полушаге обратной прогон^кой при n - ^R: T p^kn ¹ = d k , n ; при ⁿ e ( ^R , ^{- R} ] c ^{шагом A} x ^: T p,n - 1 = f к , x - e k , x • T kn .

Шаг 4.6. Организация целого временного шага для прогонки по оси z . Возвращение к шагу 4.1. Повторение расчетов до момента времени k - K .

Шаг 5 . Формирование численных значений кубоида избыточных температур и построение соответствующих графиков.

Результаты исследования

Для оценки возможности применения корреляционного алгоритма, описанного в ч. 1 статьи, и построенного алгоритма численного решения прямой задачи теплопроводности были проведены дистанционные измерения теплофизических параметров эталонных объектов путем получения их ИК-сигнатур. Съемка экспозиции объектов производилась тепловизионным приемником FLIR Tau 2, размещённым на беспилотном летательном аппарате в период с 18:45 16.10.2015 до 07:45 19.10.2015 с высоты 10 м. Общее время съемки составило 61 ч. В качестве эталонов использовались материалы с известными теплофизическими параметрами: 1. Металлическая модель танка. 2. Бетонная плита (X = 0,7 Вт^м-1\К-1). 3. Мешок с песком (X = 0,35 Вт^м-1\К-1). 4. Плита из красного полнотелого кирпича (X = 0,67 Вт^м-1\К-1). 5. Деревянная плита (X = 0,18 Вт^м-ЕК-1). 6. Мраморная плита (X = 2,9 Вт^м-1К-1). 7. Гранитная плита (X = 3,5 Вт^м-1\К-1). 8. Стальной лист (X = 58 Втм-ьК-1). 9. Плита из пенопласта (X = 0,04 Втм-ьК-1); 10. Газосиликатные блоки (X = 0,2 Вт^м-1К-1). 11. Асфальт (X = 0,7 Вт^м-1\К-1) (рис. 2).

В результате применения алгоритма корреляционной обработки кубоида ИК-изображений были получены сегментированные изображения «эталонных» материалов. Принимая во внимание зависимость порога принятия решения об обнаружении согласно критерию Неймана – – 381 –

Таблица 1. Результаты оценки необходимого количества ИК-сигнатур

Номер п/п	Объекты, по которым производился расчет выборочного коэффициента корреляции	Количество ИК-сигнатур, обеспечивающих устойчивое решение задачи сегментации
1	Плита из красного полнотелого кирпича	10
2	Стальной лист	10
3	Плита из пенопласта	12
4	Деревянная плита	14
5	Бетонная плита	9

а)

Рис. 2. Расположение эталонных материалов на грунте: а - в видимом диапазоне длин волн; б - в ИК-диапазоне длин волн

б)

Пирсона от заданной вероятности ложной тревоги, на едином сегментированном изображении в соответствии с заданным количеством «эталонов» можно выделить материалы с близкими к ним теплофизическими параметрами. Путем использования алгоритмов предварительной обработки изображений становится возможным получение четких контуров таких объектов. Однако не всегда есть возможность непрерывно и длительно производить съемку. Например, при ведении воздушной разведки в условиях работы противовоздушной обороны противника либо в условиях ограниченного запаса топлива. Возникает необходимость оценки количества ИК-сигнатур в ходе наблюдения одной и той же экспозиции объектов, обеспечивающих решение задачи сегментации изображения и последующее устойчивое решение коэффициентной обратной задачи теплопроводности. Результаты такой оценки представлены в табл. 1.

Полученные оценки эффективности сегментации изображения по критерию максимального выделения объектов по площади и различения всех 10 материалов «эталонного полигона» показали:

• –    наилучшее решение задачи сегментации достигается при построении кубоида ИК-изображения, содержащего 150 кадров с интервалом 10 мин в течение суток (рис. 3а);

• –    минимально возможным количеством ИК-изображений является три изображения, при этом интервал съемки не должен превышать 500 мин (рис. 3б);

  
  
  

  а

  
  

б

Риc. 3. Результат сегментации кубоида ИК-изображений: а – 150 кадров с интервалом 10 мин.; б – три кадра с интервалом 500 мин

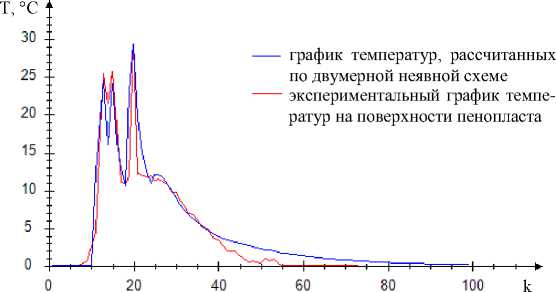
Рис. 4. Экспериментальные и рассчитанные на ЭВМ графики суточного нагрева и остывания поверхности пенопласта

• –    оптимальным количеством обрабатываемых ИК-изображений является 14 изображений с интервалом получения каждого из них около 100 мин.

На получившемся изображении четко видны почти все эталонные материалы, однако результат показал, что использование только лишь значений яркости при анализе кубоида ИК-изображений является недостаточным, так как не учитывает теплофизические процессы, проходящие в центре и по краям объектов. Для их учета необходимо разработать более сложную математическую модель, основанную на методах теплофизики, перейдя от значений яркости к температурам.

Построенное численное решение задачи (2) после восстановления функции источника тепла по данным метеорологических наблюдений погоды позволяет с приемлемой точностью рассчитывать термодинамические температуры в любой пространственно-временной точке кубоида ИК-изображений. Так, на рис. 4 представлен график зависимости изменения избыточных температур на поверхности эталонного материала «пенопласт», рассчитанных с помощью разработанного алгоритма и зарегистрированных в ходе суточного эксперимента.

Заключение

Таким образом, в статье представлена постановка и приведено алгоритмическое решение прямой задачи теплопроводности для многослойной среды с учетом граничных условий теплового баланса земной поверхности и сопряжения, учитывающая неидеальность теплового контакта соприкасающихся поверхностей. Описаны и отражены результаты натурного эксперимента корреляционной обработки кубоида ИК-изображений материалов с известными теплофизическими параметрами. Показано, что предложенный метод позволяет сегментировать объекты наблюдаемой сцены не только по относительным значениям яркостей ИК-сигнатур, но и по их теплофизическим параметрам. Использование теплофизических параметров материалов, отражающих практически не зависимые от внешних условий свойства, позволяет на качественно новом уровне решать задачу идентификации объектов как на поверхности, так и на приповерхностном слое Земли.

Работа выполнена при финансовой поддержке РФФИ (грант № 15-08-02611 А).