Корреляционно-регрессионный анализ машиностроительной отрасли РФ

В современных условиях хозяйствования перспективы развития промышленности России неразрывно связаны с уровнем развития машиностроительного комплекса страны, главной задачей которого является обеспечение всех отраслей народного хозяйства высокоэффективными машинами и оборудованием.

Машиностроение – это одна из самых емких отраслей российской промышлен- ности. Она включает в себя производство всевозможных машин, оборудования и приборов. Современное машиностроение состоит из более чем 200 подотраслей и производств. Более подробно на рисунке 1 рассмотрим структуру продукции машиностроительного комплекса РФ за 2019 год.

• ■    Автомобилестроение

  
  

• ■    Комунальное машиностроение

• ■    Станкостроение

• ■    Прочие

• ■    Машиностроение для легкой и пещевой промышленности

• ■    Тракторное и сельхоз машиностроение

• ■    Химическое и нефтяное машиностроение

• ■    Тяжелое энергетическое машиностроение

• ■    Электротехническое приборостроение

  Рис. 1. Структура продукции машиностроительного комплекса РФ за 2019 г., %

Как видно из вышепредставленной диаграммы продукция машиностроительного комплекса РФ формируется в основном от автомобилестроения доля которого в об- щей структуре продукции машиностроительного комплекса составляет 31%.

В РФ с 2014 года действует государственная программа «Развитие промышленности и повышение её конкурентоспособности» (с изменениями на 30 марта 2018 года) [1]. Данная программа содержит ряд подпрограмм по структуре отраслей, относящихся к предмету программы, в частности:

– автомобильная промышленность;

– сельскохозяйственное машиностроение, машиностроение для пищевой и перерабатывающей промышленности;

– машиностроение специализированных производств (строительно-дорожная и коммунальная техника, пожарная, аэродромная, лесная техника);

– транспортное машиностроение;

– станкоинструментальная промышленность;

– тяжелое машиностроение;

– силовая электротехника и энергетическое машиностроение.

Данная программа предусматривает создание в РФ конкурентоспособной, устойчивой и структурно сбалансированной промышленности, способной к эффектив- ному саморазвитию на основе интеграции в мировую технологическую среду, разработки и применения передовых промышленных технологий, – индустрии, нацеленной на формирование и освоение новых рынков инновационной продукции, эффективно решающей задачи обеспечения экономического развития и обороноспособности страны.

Сроки и этапы реализации государственной программы «Развитие промышленности и повышение её конкурентоспособности». Государственная программа реализуется в 2014-2021 гг., в том числе:

– первый этап – 2014-2016 гг.

– второй этап – 2016-2021 гг.

Общий объем финансирования государственной программы из федеоального бюджета РФ составляет 1060159154,4 тыс. руб. [1].

Анализ показывает, что государственная программа имеет определенные результаты. В РФ наблюдается существенный рост объема производства продукции машиностроительной отрасли [2]. На рисунке 2 изобразим динамику обьема производства продукции машиностроительной отрасли в РФ за 2014-2019 гг.

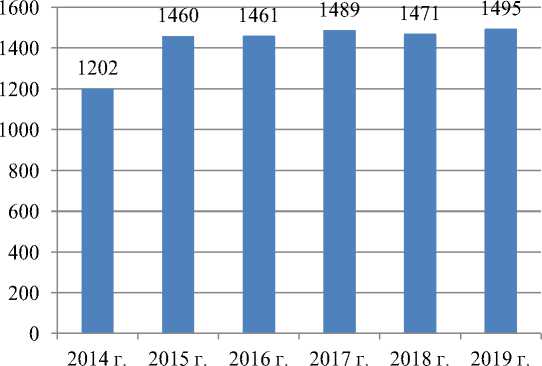
■ Обьем произвосдтва, млр.руб.

Рис. 2. Обьема производства продукции машиностроительной отрасли в РФ за 2014-2019 гг.

Как видно из вышепредставленной диаграммы обьем производства продукции машиностроительной отрасли увеличивается с каждым годом, однако в 2018 году по сравнению с 2017 годом произошло снижение обьема производства на -18

млрд. руб. За весь анализируеммый период обьем производства увеличился на 293 млрд. руб., что свидетельствует о том, что отрасль машиностраения в РФ динамично развивается и располагает значительным потенциалом, который позволит ей занять высокое место среди других отраслей российской промышленности.

Далее рассмотрим ряд факторов влияющих на обьем производства продукции машиностроительной отрасли. Обьем производства продукции машиностроительной отрасли формируется в основном от среднегодовой численности работников и числа действующих организаций. Проверим влияние данных факторов, при помощи построения регрессионой модели. Данные для построения множественной регрессии представлены в таблице 1.

Таблица 1. Данные для построения модели множественной регрессии

Год	Y обьем производства, млрд.руб.	X1 среднегодовая численность работников, тыс.чел.	X2 число действующих организаций, шт.	Yx1	Yx2	Y^2	X1^2	X2^2	X1X2
2010	1013	839	24312	84990 7	246280 56	10261 69	7039 21	591073 344	203977 68
2011	1237	837	25928	10353 69	320729 36	15301 69	7005 69	672261 184	217017 36
2012	1306	818	27812	10683 08	363224 72	17056 36	6691 24	773507 344	227502 16
2013	1352	793	28068	10721 36	379479 36	18279 04	6288 49	787812 624	222579 24
2014	1202	736	28175	88467 2	338663 50	14448 04	5416 96	793830 625	207368 00
2015	1460	721	28210	10526 60	411866 00	21316 00	5198 41	795804 100	203394 10
2016	1461	682	28219	99640 2	412279 59	21345 21	4651 24	796311 961	192453 58
2017	1489	699	28391	10408 11	422741 99	22171 21	4886 01	806048 881	198453 09
2018	1471	692	28406	10179 32	417852 26	21638 41	4788 64	806900 836	196569 52
2019	1495	711	28442	10629 45	425207 90	22350 25	5055 21	808947 364	202222 62
Сумма	13486	7528	275963	10081 142	373832 524	18416 790	5702 110	763249 8263	207153 735
Среднее значение	1348,6	752,8	27596,3	10081 14,2	373832 52,4	18416 79	5702 11	763249 826,3	207153 73,5

На основании данных таблицы 1 составим уравнение линейной множественной регрессии, Для нахождения параметров уравнения необходимо решить систему линейных уравнений относительно неизвестных параметров, которая представлена в соответствии с формулой 1.

an+∑х1+∑х2=∑у

∑х1+∑х12+∑х1х2=∑ух1

∑х2+∑х1х2+∑х22 = Syx2

Далее, подставим значения из таблицы в формулу и составим систему линейных уравнений.

10+7528+275963=13486

7528 + 5702110 + 207153735 = 10081142 275963 + 207153735 + 7632498263 = 373832524

Решим систему линейного уравнения по методу Крамера.

∆	10  7528  275963 7528+5702110+207153735   = 2439228146338

275963 + 207153735 + 7632498263

13486  7528  275963

= 401869304889344

∆1   10081142  5702110  207153735

373832524  207153735  7632498263

∆2

10  13486  275963

7528  10081142  207153735

275963  373832524  7632498263

= -2181631783776

∆3

10  7528  13486

7528  5702110  10081142

275963  207153735  373832524

= 164152664672

На основании найденных определителей, найдем параметры уравнения множественной

регрессии.

X1=

X2=

X3=

Δ 1

Δ

Δ 2

Δ

Δ 3

Δ

-2181631783776

164,7527

= - 0,8944

= 0,0673

Таким образом, получаем следующие уравнение множественной регрессии:

Y = 164,7527-0,8944X1 + 0,0673X2

Полученное уровнение показывает взаимосвязь между показателем обьема производства и числом действующих организаций. Из данного уравнения видно, что с ростом числа действующих организаций на 1 ед. обьем производства возрастает на 0,7 млрд. руб. Среднегодовая численность работников напротив снижает обьем производства на 0,89 млрд. руб.

Далее рассмотрим взаимосвязь каждого отдельного взятого фактора с показателем обьема производства, для этого рассчитаем парные коэффициенты корреляции. Для того что бы рассчитать парные коэффициенты корреляции необходимо в первую очередь найти среднеквадратические отклонения. Расчет среднеквадратических отклонений представим в таблице 2.

Таблица 2. Расчет среднеквадратических отклонений

Признак	Формула расчета	Расчет	Значение
σу	у^2 - (у)	V1841679 - 1348, 62	151,52
σх1	х1 5 - х1 )2	V570211 - 752, 82	59,19
σх2	х2 2 - х2 )2	V763249826,3 - 27596, 32	1301,56

Подставим найденные среднеквадратические отклонения в формулу 2, и рассчитаем парные коэффициенты корреляции.

_ ху-х ∗ у rxy =

ay∗ ax ryx1= ryx2=

1008114 , 2-752 , 8 ∗ 1348 , 6 151,52∗59,19

= - 0,793

37383252 , 4 - 27596 , 3 ∗ 1348, 6 151,52∗1301,56

0,846

ryx1x2 =

20715373,5-27596,3∗752,8

59,19∗1301,56

= - 0,767

На основе рассчитанных коэффициентов парной корреляции можно сделать вывод, что одним из самых значимых факторов оказывающих влияние на показатель обьема производства является фактор (X2) число действующих организаций.

Используя шкалу Чеддока для выявления характеристики силы связи можно утверждать, что фактор x2 (число дейст- вующих организаций) оказывает высокую связь (0,846) на результативный признак Y.

Из полученных параметров уравнения множественной регрессии найдем стандартизированное уравнение регрессии, ко- торое представлено в соответствии с формулой 3.

ty =β1tx1+ β2tx2                     (3)

Найдем β1; β2; β3 используя уже имеющиеся параметры уравнения множественной регрессии, расчет представим в соответствии с формулой 4

β = bn*

β1= b1*   = -0,8944* ^ ^,   = -0,349

β2= b2*   = 0,0673* 1301 ^, 56 = 0,578

^r         ay              151,         ^,

axn ay

Стандартизированное уравнение регрессии будет иметь вид:

ty = 0,349 tx1+0,578tx2

Стандартизированные коэффициенты регрессии можно сравнить между собой. Так как β2>β1 то можно сказать, число действующих организаций оказывают большее влияние на обьем производства чем среднегодовая численность работников.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности, которые находятся в соответствии с формулой 5.

Э = bi *

yi

Параметры b1и b2 нам уже известны, подставим их в формулу 5 и вычислим коэффициент эластичности.

Э1= -0,8944 * 752 ^, ® = -0,499

Э2= 0,0673* 27596 ^, - = 1,377 ^, , ^,

Коэффициент эластичности показывает, насколько процентов в среднем изменяется признак-результат (у) с увеличением признака-фактора хi на 1% от своего среднего уровня при фиксированном положении других факторов модели. Из полученных значений коэффициентов эластичности можно утверждать, что коэффициент эластичности Э1<1, следовательно его влияние на результативный признак Y незначительно. Коэффициент эластичности Э2>1 следовательно, он существенно влияет на результативный признак Y. Таким образом, подтверждается большее влияние на результат (у) фактора X2.

В результате расчетов было получено уравнение множественной регрессии: Y = 164,7527-0,8944X 1 + 0,0673X 2 . Возможна экономическая интерпретация параметров модели: увеличение X 1 на 1 ед.изм. приводит к уменьшению Y в среднем на 0,894 ед.изм.; увеличение X 2 на 1 ед.изм. приводит к увеличению Y в среднем на 0,0673 ед.изм. По максимальному коэффициенту β 2 =0,578 можно сделать вывод, что наибольшее влияние на результат Y оказывает фактор X 2 .

Таким образом, можно сделать вывод о том, что основопологающим фактором оказывающим влияние на обьем производства машиностроительной отрасли является фактор числа действующих организаций.