Корреляционно-регрессионный анализ влияния факторов на урожайность зерновых культур

Экономико-статистический анализ производственно-хозяйственной деятельности предприятия играет важную роль в обеспечении повышения эффективности производства. Он является существенной составной частью экономических методов управления. Анализ является базой планирования, средством оценки качества планирования и выполнения плана.

Изучение взаимосвязей - одна из важнейших задач экономикостатистического анализа. Статистика различает компонентные и факторные связи.

Компонентные связи характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель как множители. Например, динамика затрат на 1 руб. товарной продукции зависит от динамики себестоимости и объема производства продукции.

Факторные связи проявляются в согласованной вариации изучаемых показателей. При корреляционной факторной связи изменение результативного признака y обусловлено не полностью влиянием факторного признака х , а лишь частично, так как возможно влияние других факторов. При изучении корреляционной связи решаются следующие основные задачи:

• -    выделение основных причинно-следственных связей между изучаемыми показателями;

• -    построение модели;

• -    оценка линии регрессии;

• -    измерение тесноты связи, т.е. определение роли изучаемого фактора в формировании результативного признака;

• -    проверка существенности связи, т.е. доказательство неслучайного характера выявленных закономерностей связи.

Статистика разработала много методов изучения факторных связей: графический, метод аналитических группировок, корреляционнорегрессионный анализ. Рассмотрим поподробнее один из них – это корреляционно-регрессионный анализ.

Корреляционно регрессионный анализ - комплекс методов, основанный на построении регрессионной модели. Наиболее разработанной в статистике является методика парной корреляции, рассматривающая влияние одного факторного признака ( x ) на результативный ( y ).

Рассмотрим влияния внесения удобрений в ц\га на урожайность зерновых культур Орловской области за период 1997-2012.

Таблица 1 Исходные данные

Годы	Доза внесения удобрений, ц/га	Урожайность озимой пшеницы, ц/га
1	2	3
1997	54	19,1
1998	58	20,0
1999	52	19,0
2000	65	19,3
2001	59	22,9
2002	54	27,0
2003	58	24,5
2004	70	23,3
2005	61	24,0
2006	62	24,1
2007	62	23,0
2008	69	31,4
1	2	3
2009	67	30,7
2010	81	21,6
2011	83	22,4
2012	71	27,2

Результативный признак (у) – урожайность зерновых культур, ц/га

Факторный признак (х) – доза внесения минеральных удобрений, ц/га

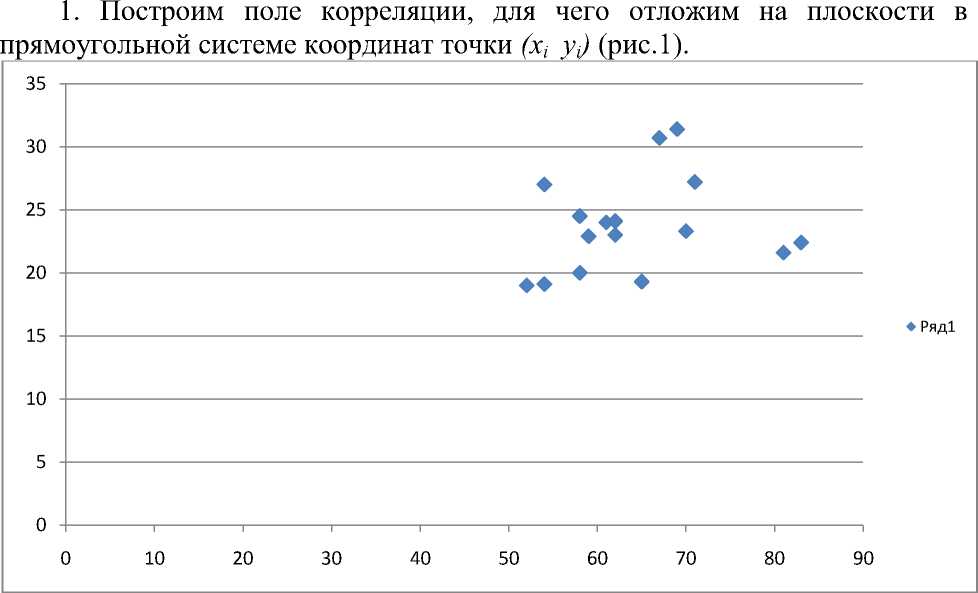
Рис. 1 Поле корреляции

Расположение точек на графике не позволяет точно определить тип уравнения регрессии. Для выявления типа зависимости воспользуемся экспериментальным методом.

Для расчета параметров линейной регрессии построим расчетную таблицу 2.

Таблица 2 – Расчетные значения

№	х	у	xy	2 х	у2	у	у - у -—- х 100% у
1	54	19,1	1031,40	2916,00	364,81	23,06	20,73
2	58	20	1160,00	3364,00	400,00	23,42	17,10
3	52	19	988,00	2704,00	361,00	22,88	20,42
4	65	19,3	1254,50	4225,00	372,49	24,05	24,61
5	59	22,9	1351,10	3481,00	524,41	23,51	2,66
6	54	27	1458,00	2916,00	729,00	23,06	14,59
7	58	24,5	1421,00	3364,00	600,25	23,42	4,41
8	70	23,3	1631,00	4900,00	542,89	24,50	5,15
9	61	24	1464,00	3721,00	576,00	23,69	1,29
10	62	24,1	1494,20	3844,00	580,81	23,78	1,33

11	62	23	1426,00	3844,00	529,00	23,78	3,39
12	69	31,4	2166,60	4761,00	985,96	24,41	22,26
13	67	30,7	2056,90	4489,00	942,49	24,23	21,07
14	81	21,6	1749,60	6561,00	466,56	25,49	18,01
15	83	22,4	1859,20	6889,00	501,76	25,67	14,60
16	71	27,2	1931,20	5041,00	739,84	24,59	9,60
Итого	1026,00	379,50	24442,70	67020,00	9217,27	383,54	201,23
Ср.зн	64,13	23,72	1527,67	4188,75	576,08	х	12,58

Построим линейное уравнение парной регрессии у по х . Используя данные табл ицы 2, имеем:

y ⋅ x - y ⋅ x

β= x ² - x ²    =0,09

a = ^{y - β ⋅ x} = 18,2

Тогда линейное уравнение парной регрессии имеет вид:

YX = 18,2 + 0,09 *X

Полученное уравнение показывает, что с увеличением дозы внесения органических уравнений на l ц/га урожайность зерновых культур возрастает в среднем на 0,09 ц/га.

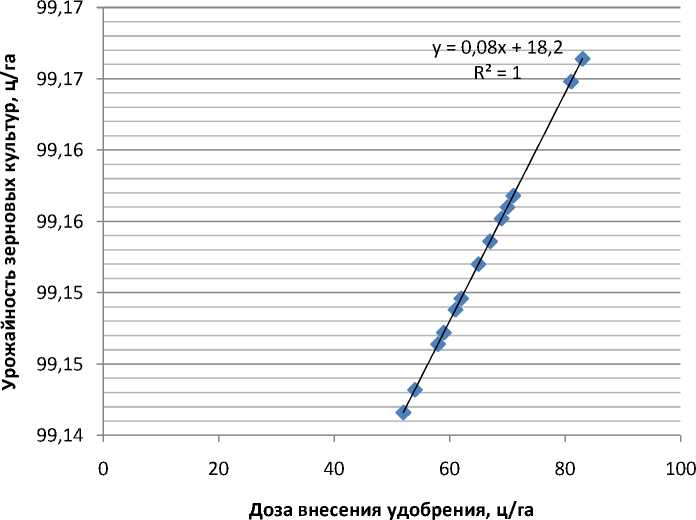
Рис. 2. Зависимость между дозой внесения минеральных удобрений и урожайностью зерновых культур (линейная регрессия).

Подставляя в полученное уравнение регрессии значения x_i из исходных данных определяем теоретические (выровненные) значения результативного признака (табл.2).

При линейной корреляции между х и у исчисляют парный линейный коэффициент корреляции r. Он принимает значения в интервале -1 < r < 1. Знак коэффициента корреляции показывает направление связи: «+» – связь прямая, «–» – связь обратная. Абсолютная величина характеризует степень тесноты связи.

Учитывая:

_ / X ( Xi ^- X "f          ^ = I X ( у! ^- y ) 2

σХ =                       Y i         n      =8,76             n =3,67

оценим тесноту линейной связи с помощью линейного коэффициента парной корреляции

§х

^ = Р-^ =0,21

Связь между факторами прямая. В соответствии со шкалой Чеддока теснота характеризуется как слабая.

Изменение результативного признака у обусловлено вариацией факторного признака х. Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака характеризует коэффициент детерминации D. Коэффициент детерминации – квадрат коэффициента корреляции.

R²=r ху ²•100%=4,34%

Следовательно, вариация урожайности зерновых культур на 4,34 % объясняется вариацией дозы внесения удобрений, а остальные вариации урожайности обусловлены изменением других, не учтенных в модели факторов.

А = n "^X y I ' ¹⁰⁰% = n ^X A i =12,58 %.

В среднем расчетные значения отклоняются от фактических, на 12,58%. Это входит в допустимый предел, следовательно, качество построенной модели высокое.

Для оценки силы связи признаков у и х найдем средний коэффициент эластичности:

Э = f'(x ) * x _ 6^х_

■      y .= a + ex = 0,24%

Таким образом, в среднем на 0,24% по совокупности изменится урожайность зерновых культур от своей средней величины при изменении дозы внесения удобрений на 1% от своего среднего значения.

Для оценки статистической надежности результатов используем F-критерий Фишера.

Выдвигаем нулевую гипотезу Но о статистической незначимости полученного уравнения регрессии. 2

Е фа„. = = ^ — r ( _n -2)=0,63

Сравним фактическое значение критерия Фишера с табличным. Для этого выпишем значения критерия Фишера из таблицы «Значения F-критерия Фишера при уровне значимости а =0.05» (приложение 1).

В нашем примере k 1 =1; k=16-1-1=14.

Таким образом. F табл . =4,60 при ^Y =0,05.

Т.к. Fфакт.< F-табл., то при заданном уровне вероятности у=0,05 следует принять нулевую гипотезу о статистической незначимости уравнения регрессии и показателя тесноты связи.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей.

Выдвигаем гипотезу Н о о статистически незначимом отличии показателей регрессии от нуля а = Р =г _ух =0.

Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки:

t в

в

а

m e ; ^а m a ;

r tr = --- mr

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

т р =

та

■-- '■" ■ V 0,003

£ (х-х)л2

^-У)² *   ^^{х 2}_ = 13 4

п-2    п*Х(х-х)2

1—r тг = /--- =0,26

ГХ   \ п-2

Сравнивая фактическое и критическое (табличное) значения t-статистики принимаем или отвергаем гипотезу Но.

Если 1 _таб_л <  Т ф_акт, то Но отклоняется, т.е. а , в , r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если 1 _табл >  t ф_акт, то гипотеза Но не отклоняется и признается случайная природа формирования а , в , г.

1Р =

^а =

^ х

—=27,3

т р

— =1,35

та

-^х5- = 0,80 ^т гх

t табл при уровне значимости у =0,05 и числе степеней свободы равных 16-2=14 равно 2,1448 (приложение 2).

tв > t-табл,    ta < tтабл,     tr < t-табл, следовательно нулевая гипотеза о несущественности коэффициентов корреляции и регрессии принимается , т. е. r, а статистически незначимы, а вот β является статистически значимым.

Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:

∆ α = t табл m α = 2,1448 ∙13,4=28,74

∆ β = t табл m β = 2,1448 ∙0,003=2,15

Доверительные интервалы:

Для параметра α : (-10,62; 46,86)

Для параметра β : (2,06; 2,24)

Анализ верхних и нижних границ доверительных интервалов приводит к выводу, что с вероятностью p = 1–γ = 0,95 параметры α и β находятся в указанных пределах, причем параметра a являются статистически незначимыми, т.к. в границы доверительного интервала попадает ноль, а b статистически значимым.