Корреляционные функции полей напряжений и деформаций в микронеоднородных средах
Автор: Ташкинов М.А., Михайлова Н.В.
Статья в выпуске: 4, 2016 года.
Бесплатный доступ
Статья посвящена разработке метода вычисления полей микроструктурных напряжений и деформаций в многокомпонентных средахна основе вычисления статистических характеристик локальных полей напряжений и деформаций в компонентах, позволяющих учитывать заданные геометрические и физико-механические свойства компонентов. Исследуются представительные объемы структурно-неоднородных материалов, состоящие из нескольких компонентов. Предполагается, что компоненты являются однородными и изотропными. Для описания внутренней геометрии и оценки пространственного взаимодействия между микроструктурными компонентами используется набор структурных моментных функций различных порядков. Поведение отдельных компонентов микроструктуры при нагружении представительного объема оценивается с помощью статистических характеристик локальных полей напряжений и деформаций. В качестве характеристик процессов деформирования использованы статистические моментные функции полей напряжений и деформаций в компонентах неоднородной среды. Аналитические выражения для статистических моментов и корреляционных функций полей напряжений и деформаций находятся с помощью статистического осреднения интегродифференциальных уравнений, содержащих моментные функции и получаемых на основе решения стохастических краевых задач в упругой и упругопластической постановке. Рассмотрены некоторые частные случаи типичных неоднородных сред со случайной микроструктурой. Построены корреляционные функции напряжений и деформаций для разреженных структур со сферическими и эллипсоидальными полыми включениями в упругом и упругопластическом случае. Проведено исследование и выбор аппроксимирующих зависимостей для полученных корреляционных функций. Полученные численные результаты могут использоваться дляоценки механического поведения микроструктурных компонентов неоднородной среды при нагружении, а также для предсказания момента начала разрушения.
Пористые материалы, упругопластическая краевая задача, случайная структура, моментные функции, поля напряжений и деформаций, функция грина, статистическое осреднение
Короткий адрес: https://sciup.org/146211651
IDR: 146211651 | УДК: 539.3 | DOI: 10.15593/perm.mech/2016.4.03
Текст научной статьи Корреляционные функции полей напряжений и деформаций в микронеоднородных средах
PNRPU MECHANICS BULLETIN
Важной и актуальной проблемой в механикенеоднородных материаловявляется разработка моделей механики неоднородных средсо случайной структурой, учитывающих особенности реальной структуры композиционных материалов, процессы нелинейного деформирования, появление и развитие областей разрушения в структуре микронеодно-родных материалов задолго до полного разрушения конструкций.
Доказано, что влияние распределения включений играет решающую роль в макроскопическом поведении неоднородных сред [1–4]. Таким образом, создание точных математических моделей позволяет предсказывать эффективное механическое поведение с учетом особенностей микроструктуры, таких как размер, объемная доля, ориентация, дисперсия и кластеризация составляющих компонентов.
Распространенным направлением в микромеханике материалов со случайной структурой являются методы статистической механики для систем многих частиц, в которых используются многоточечные статистики для напряжений, деформаций и полей смещений, для описания взаимодействия неоднородностей. Основы статистической механики были заложены в работах М. Берана, В.А. Ломакина, Т.Д. Шермегора [6, 8, 9, 11, 12] и в дальнейшем широкое распространение получили во многих научных школах [1, 5, 7, 10, 13, 14]. Представленные характеристики полей учитывают хаотичность расположения элементов в структуре, а также статистическую дисперсию свойств компонентов. Например, эффективные упругие свойства могут быть оценены на основе статистических моментов первого порядка полей напряжений и структурных моментных функций [7, 8, 13, 15]. Моменты высшего порядка используются для исследования распределения напряжений и деформаций в компонентах. Методы, связанные с описанием гетерогенных структур с помощью корреляционных функций, также используются для отождествления моделей микроструктуры с экспериментально анализируемыми образцами материалов [16–18].
Анализ деформирования и разрушения в рамках статистических подходов основан на разработке многоуровневых математических моделей и численных алгоритмов для решения задачи микромеханического описания процессов деформации представительного объема материала [5–8, 13, 14, 19]. Параметры таких процессов зависят от конкретных характеристик полей структурных напряжений и деформаций, которые могут быть определены из решения стохастических краевых задач, где уравнения и граничные условия содержат случайные величины.
Целью данной работы является разработка аналитического инструментария для анализа полей микроструктурных напряжений и деформаций в многокомпонентных неоднородных средах, позволяющего учитывать геометрические и физико-механические свойства компонентов, на основе построения корреляционных функций полей напряжений и деформаций. В разработанных ранее подходах в качестве статистических характеристик полей деформирования использовались статистические моменты, которыеявляются константами для конкретного представительного объема при заданном нагружении [6–8, 20– 28]. При этом для оценки пространственного взаимодействия между микроструктурными компонентами используется набор структурных моментных функций различных поряд-ков.Разработанная в данной работе аналитическая модель позволяет поставить в соответствие структурным моментным функциям корреляционные функции полей напряжений и деформаций, представляющие собой моментные функции второго порядка.
1. Постановка и решение стохастических краевых задач неоднородных сред
Аналитические выражения для корреляционных функций полей напряжений и деформаций находятся на основе решения стохастических краевых задач в упругой и упругопластической постановке. Стохастическая краевая задача теории упругости для композитов со случайной структурой в некоторой области (представительном объеме) V записывается следующим образом:
°нА Г)=0,(1)
- j( r) = 2 (чД r)+«»( r)),
° j(F ) = Cyki (r )e и.(F),
U (r )lFeru = ejrj , где Cijkl (r) - тензор структурных модулей упругости; ej - компоненты симметричного тензора малых макродеформаций, с помощью которого определяется нагружение представительного объема; r - радиус-вектор с компонентами (x1, x2, x3); Г u - поверхность представительного объема. Между компонентами выполняются условия идеального кон-(I) (M) (I) (M)
такта u, = u, , o„ ) n; = ст(г ) п, .
ii ij j ij j
Стохастическая краевая задача упругости композитов с помощью функции Грина сводится к интегродифференциальному уравнению относительно пульсаций перемещений [6-8, 22, 24], которое в первом и втором приближении для двухфазных материалов имеют следующий вид:
u ^ ’( r) = = >, €-*, j G„ , ( r, r ) ( X ; ( r ) V V 1 , (5)
V
u ;®( r ) = e l, C „n„ j G „, ( r , r ) l X; ( r ) I , . dV + V Vi
e oq ^ m.kl ^ fsoq
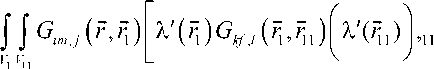
s
■ i . dV, dV
где Gim (r, r) функция Грина; , j обозначение производной % ; X‘(r) = X(F) — (X(F)^ / ° rj флуктуация случайной индикаторной функции в точке; Cmnkl = CImnkl — CmMk - разность тен зоров структурных модулей упругости включений и матрицы; ukl (r) - поле флуктуаций перемещений в представительном объеме, которое является решением краевой задачи теории упругости или упругопластичности в стохастической постановке.
С учетом разложения полей деформаций и напряжений на среднюю составляющую и пульсацию для пульсаций структурных напряжений и деформаций справедливы следующие соотношения:
ё j r ) = 2 ( u j r ) + u j. ( r ) ) • O y(r) =° y( r ) —<^ j ( r ) > .
Тогда получаем dj (r)(1) =1 eklCm„kt j (Gm,j (r,F) + Gjm,i (r, F ))X' (F ) 1 .dV 2 V
^j ( F ) (2) =
Г eklCmnkl j(Gim,j (F , F ) + Gjm, (F , F )) X(F ),i.
V V
dV 1 +
+ e ofC-. jj( G„ , j ( F , F ) + G,. , i ( F , F ) ) G f , , ( F ■ r i X^’ CF ) X‘ < r i )) „ , , . dVdV , V V 1 i
^' ij ( F ) = Cijmn ( F ) e m. - < C jm. ( r ) ^ mn ( r ) > + Cijmn ( r ) S mn ( F ) .
Здесь комбинации типа X‘ ( F ) X‘ ( F 1 ) при последующем осреднении образуют структурные моментные функции, значения которых могут быть получены для геометрии исследуемых представительных объемов. Выражения (7)-(9) используются для получения аналитического представления корреляционных функций полей напряжений и деформаций.
Использование второго приближения(9) предполагает использование структурных моментных функций более высокого порядка, при этом значительно увеличивается время расчета. Установлено, что для исследуемого класса пористых композитов вклад, вноси- мый в результаты вторым приближением, является незначительным (разница с результатами в первом приближении составляет 2-4%), поэтому с целью экономии вычислительных ресурсов представляется целесообразным использование первого приближения (8).
2. Аналитические выражения для многоточечных корреляционных функций полей напряжений и деформаций
Напряженно-деформированное состояние представительного объема композита характеризуют моменты и моментные функции полей микроструктурных напряжений и деформаций. Существуют безусловные и условные статистические характеристики, предназначенные для описания механического поведения композита как макрооднородного материала и его компонентов в отдельности [7, 8]. Выражения для многоточечных условных и безусловных моментных функций стохастических полей напряжений и деформаций в представительных объемах композитов позволяют описывать взаимосвязь полей в удаленных на различное расстояние точках и при необходимости вычислять значения моментов случайных полей в произвольных точках представительного объема.
В общем виде моментные функции n -го порядка полей напряжений могут быть получены из выражения
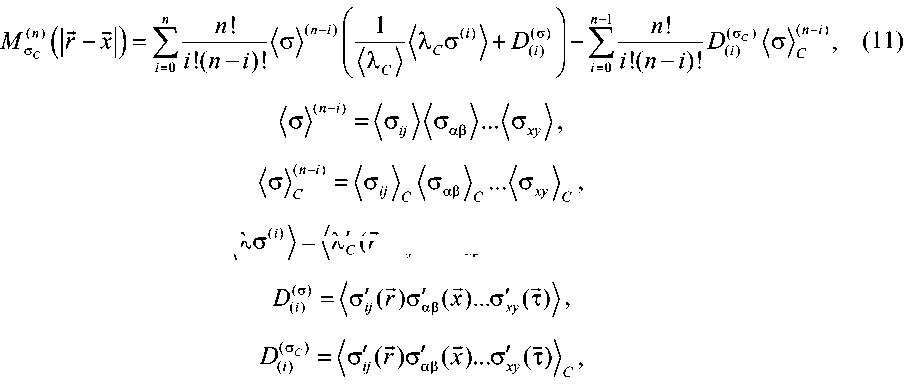
V\ Cc
О = \О ij)\ Oa» /"A ° xy
O) = ( O - ) (On ) ...( О
/ c \ ij / c \ ав / c \ xy где ( ) оператор осреднения есть оператор математического ожидания. Для случайных однородных эргодических полей осреднение по объему совпадает со статистическим осреднением. Xc (F) - индикаторная функция для представительного объема, равная 1, если радиус-вектор r находится в компоненте С, и 0 - в остальных случаях, XC(r) = Xc(F) -(Xc(F)) - флуктуация индикаторной функции, величина u.c(F)^ определяет объемную долю компоненты c в представительном объеме.
В данных формулах случайные поля флуктуаций напряжений d j ( r ) выражаются через поле структурных модулей упругости c ijkl ( r ) = / c j; ( r ф + Ci jkl ( r ) , и флуктуации полей деформаций a j ( F ) формулой (10).
Для многокомпонентного композита в общем виде флуктуации структурных модулей упругости в i -м компоненте выражаются в следующем виде в упругом (13) и упругопластическом случае (14):
m
c.nk(r)=£(NO)+.(r))C .„ i=1
m
C .n„ ( r ) = E (^ i ( r» ■'( r ) ) C .'.« <(6*)M , A ,„)-( C .n „( r )), ( 14 )
i = 1
A / / — \ /— \ — где л» =Vwи» 8 - ■
- 3 8 kk 8 у — девиаторная часть тензора деформаций.
Непосредственно получить решение упругопластической краевой задачи обычно не удается, так как связь тензоров напряжений и деформаций является физически нелинейной, и применить к ней традиционные методы механики затруднительно. Поэтому системе уравнений структурно-феноменологической модели, как и в упругой задаче, ставится в соответствие система уравнений для среды с эффективными свойствами. Чтобы воспользоваться статистическими методами, физические уравнения (которые записываются через определяющие соотношения в инвариантной форме: оц(r) = [3K(г,у®, j^)j + 2р(г,у®, j^)D^]gи (r)) необходимо линеаризовать при определенных допущениях. Для решения поставленной задачи применяется вариант метода статистического осреднения, в пределах объема каждого компонента композита пренебрегаются пульсации деформаций, стоящие под знаком материальных функций н ,) (j™, j н ,) (
< р >
< 8 ii > ( i ) ,
л f , . ) , K f ,
(i
(1) /2П=^ f
( Jb , J 8 ) Jvf , . ( <8 ii
> f , .
Л f , . ) .
С учетом формулы (10) и с помощью процедуры осреднения получены выражения для моментных функций полей напряжений, описывающих представительный объем как макрооднородный. Так, соотношение для безусловной корреляционной функции полей напряжений имеет вид
M ° C ’ (I r - x ) = O j (■' '<( x^ = .e»(kC*hD 2 1 * +
+ ««Cw (C .6.) (.' (r 8( x )) + e„C*h (C „)(.' ( r K ( r) +
+ ( C „k,)( C .„ . )(= k, ( r X h (-Г)) - «AkC .„ h {.' (W X )< h ( X )) - (15)
- e . ДА .6. h (.' ( r W(( r ) - C aw ДД(.'xX X( x ) e k, ( r) -
C ijkl \ C «Рф h / \Л ( r ) 8 . h ( r ) 8 kl ( x )/ + C ijkl C ap. h \Л ( r ) . ( x ) 8 kl ( r ) 8 . h ( x )/
С учетом разложения полей деформаций и напряжений на средние составляющие и пульсации (7) для многокомпонентной неоднородной среды корреляционные функции (моментные функции второго порядка) полей деформаций и напряжений в компоненте С записываются в следующем виде:
M 8 ( с 2) (I r - ^^1 ) = (8' / ( r К₽ ( x )} C = (8 j ( r K₽ ( x )) + e j e ap -(8 ^ C (8 ap ) C +
. . 1 r )) (( . C ( r ) 8 ' у ( r Kp ( x )) + e ij (. C ( r Kp ( x )) + e ap (. C ( r ) 8 ' у ( r ))) ,
M Z ’ (I r - ^^1 ) = (° i/ ( r Hp ( X )) C = (° i/ ( r Hp ( X )} + (° ij) (°ap ) - (° ij X (°ap ) C +
+ -^“^ (( X C ( r ) O i/ ( r Kp ( XX + (° j ) (X C ( r Kp ( XX + (° ap ) (. C ( r )о'у ( r X ) •
Средние значения тензора деформаций и напряжений в компоненте С принимают вид [7, 8]
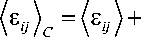
(i c h ^ ( r ) Е , ( r ) ) ,
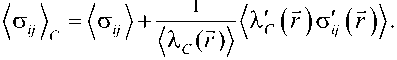
Искомые моментные функции полей напряжений и полей деформаций как в компонентах неоднородной среды (16), (17), так и гомогенизированном представительном объеме (15) зависят от ряда безусловных и смешанных функций различных порядков, в которые входят флуктуации полей деформации a , ( r ) , а также многоточечные структурные моментные функции K n ) ( г , r,...,rn ), которые содержат статистическую информацию о геометрии неоднородной структуры композитов. Для многокомпонентной среды структурные моментные функции строятся для каждой компоненты в отдельности:
= (( X c ( r ) -(X c (F» )( X c ( r ) -(X c ( r )) ) ... ( X c ( r n ) X c ( r, »)) .
Значения структурных моментных функций могут быть получены на основе анализа геометрической модели представительного объема [16, 18, 24].
В качестве примера далее приведены некоторые безусловные корреляционные функции полей деформаций, входящие в выражения для корреляционных функций полей напряжений и полученные с использованием первого и второго приближения решения стохастической краевой задачи в случае двухфазного композита:
(=-,(г)^(Г) ' = 1 emne„Ckm,C„„J J (G.,,(r,r) + G,^r,r))(G„,(x,x) + G„,(x,x))x 4
x K <2) ( r. , x .), „ dVdV X V 1 " 1 /, l U 1 2
-\\(2)
(a, (r Rp(x))
1C , 4 mmnkl 7ПФ h
r eф. J J( Gm, r, r) + G,mA -,X))(G.„ (x, x) + G„,. (x, x) )x
I xKX2)( r, x),, .1, dV2 dV +
+ e ki e bd C vwbd J J J ( C„A r , X ) + C„ ( r , X ) )( G «„, ( x , x ) + G ,„. ( г , x ) ) x
V V 2 V 21
x G Ф ., ( x , x 2 ) K X 3) ( r , - x , x 2 ) ,1 .„j . dV 2 l dV 2 dV1 +
+ е ф . e oq C fsoq J J J ( G m, r , r ) + G ,mi (r , r ) )( G „,( x , x ) + G 6„( x , x 1 ) ) x
V V , V 1
x G k,, ( . , г ) K X 3) ( . , x„r ) 1 , Л2 , dV 1 dV dV 1 +
V V 2 V 1 V 21
4K(4)(r. X, Fm xGkf,i (X,r)Gф.,h (x,x2) X (1’ |,r2, 2) dV21 dV11 dV2dV1 .
d r 1 , d x 1 n d r2 s d x 2 w J
Таким образом, получены выражения для вычисления моментных функций первого и второго порядков полей напряжений и деформаций как в целом так и в компонентах композита с использованием структурных моментных функций высших порядков.
3. Трехмерные модели внутренней полидисперсной структуры текстурированных матричных композитов с эллипсоидальными включениями
Для реализации методики были построены трехмерные модели внутренней полидис-персной структуры исследуемых материалов – двухкомпонентных текстурированных матричных композитов с эллипсоидальными включениями. В отличие от хаотически армированных композитов рассматривается текстурированный композит с эллипсоидальными включениями, имеющими определенную пространственную ориентацию. Предполагается, что включения расположены в матрице равномерно. Также было введено условие, согласно которому включения не могут пересекаться. Для создания геометрической модели был использован алгоритм, позволяющий синтезировать полидисперсные эллипсоидальные включения в представительном объеме заданного размера.
Для проверки выполнения условия отсутствия пересечений эллипсоидов каждое включе- ние описывается параллелепипедом, для которого проверяется пересечение с другими, уже существующими. При условии, что все эллипсоиды находятся в одной системе координат, необходимо отдельно сравнить минимумы и максимумы координат вершин параллелепипедов отдельно по трем осям. Так, если первый параллелепипед определен значениями координат
Ax min ,
A A .
x _max , y _min
A y_max ,
min , Az max , а второй Bx min , Bx max ,
^^^™
^^^™
в в _ s _ y _min , y_max , z_min ,
B z max , то эллипсоиды пересекаются, если выполняются все неравенства: A min < B x max
А >В А x_max x_min , y_min
y _max , Ay _max > By _min , Az _min
*z max , Az max > Bz min . ^^^^» ^^^^s ^^^^e
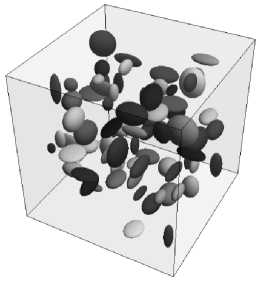
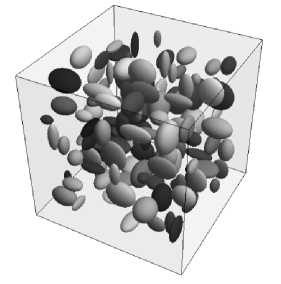
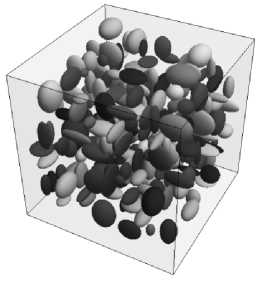
На рис. 1приведены изображения некоторых полученных моделей представительных объемов с различной объемной долей эллипсоидальных включений.
в
а б
Рис. 1. Представительные объемы структур с эллипсоидальными включениями с различной объемной долей: а – 5 %, количество включений 77; б – 10 %, количество включений 158; в – 15 %, количество включений 245
Fig. 1. Representative volumes of structures with ellipsoidal inclusionsof different volume fractions: а – 5 %, the number of inclusions is 77; b – 10 %, the number of inclusions is 158; c – 15 %, the number of inclusions is 245
Для исследуемых структур с эллипсоидальными включениями получены значения структурных моментных функций высших порядков, а также рассчитаны коэффициенты аналитических аппроксимирующих выражений для структурных моментных функций, необходимых для вычисления моментных функций полей напряжений и деформаций. В качестве выражений для аппроксимации использованы следующие зависимости [23, 27]:
f (2) ( |F - r i |) = exP ( - c i r - r i |) [ cos ( c 2 r - r i |) + c 3 sin ( c 2 r - r 1| ) ] , ( 23)
( n ) f X
^ ^
r — r 1 ) = exp ( - c 1
^ ^ 1^ ^ 2
I r — Г 1 1) cos I c 2 r — r j I ,
где (23) использовано для аппроксимации функций второго порядка; (24) – для функций порядка выше второго. Для построения моментных функций высшего порядка шаг между радиусами-векторами принимался равным. На рис. 2 отображены графики аппроксимированных моментных функций различных порядков для структуры с объемной долей включений 10 %.
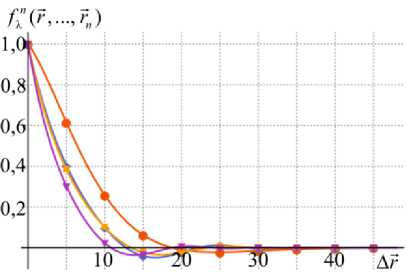
Рис. 2. Моментные функции различных порядков для структуры с объемной долей эллипсоидальных включений 10%: – моментная функций второго порядка; – моментная функция третьего порядка;
– моментная функция четвертого порядка; – моментная функция пятого порядка
Fig. 2. Correlation functions of different orders for a structure with a volume fraction of ellipsoidal inclusions amounting to 10 %: – is the second order correlation function; is the third order correlation function; – is the fourth order correlation function; – is the fifth order correlation function
4. Значения моментных функций полей деформирования в упругом случае при различных условиях нагружения и физико-механических характеристиках компонентов композитов
Для получения значений условных (в компонентах композита) и безусловных (для представительного объема как целого) моментных функций полей напряжений и деформаций в представительных объемах и их компонентах использовано решение стохастической упругой и упругопластической краевой задачи в первом и втором приближении. В качестве входных параметров для вычислений выступают константы, характеризующие свойства компонентов представительного объема и входящие в функции Грина в подын- тегральных выражениях, а также геометрические свойства компонентов, определяемые структурными моментными функциями. Нагружение представительного объема задается в виде граничных условий стохастической краевой задачи.
Алгоритм численной реализации методики заключается в вычислении значений интегралов в выражениях для корреляционных функций при необходимых комбинациях индексов в зависимости от расстояния между радиусами-векторами r и х . При этом значения моментной функции M * 2' ( r - х| ) находятся путем осреднения моментов 8у ( r )8 Lp ( х ) для заданного расстоянии между радиусами-векторами r -х| , вычисленных в дискретных точках представительного объема V . Точность вычисления значений моментной функции определяется частотой (шагом) дискретизации представительного объема.
Для реализации методик численного вычисления значений моментных функций полей деформирования в упругом и упругопластическом случае при различных условиях нагружения представительных объемов и физико-механических характеристиках компонентов созданы программные инструменты, реализованные в виде программного кода в среде Wolfram Mathematica, с использованием возможностей встроенных функций и параллельных вычислений, а также в среде С++. Используемые численные методики аналогичны методикам при вычислении моментов полей напряжений и деформаций, которые подробно рассмотрены в работах [24, 28].
На приведенных ниже рисунках представлены некоторые результаты для моментных функций полей деформаций в представительном объеме пористого композита. Представлены дискретные значения и их интерполяция. Для расчетов был выбран частный случай деформирования как чистый сдвиг.
Для упругой краевой задачи был задан тензор макродеформаций eij на границе представительного объема в виде граничных условий (4), равный e 12 = e 21 = 10 - 6 . Упругие свойства матрицы заданы следующими величинами: модуль упругости матрицы пористого композита E M = 2^10 5 МПа; коэффициент Пуассона v m = 0,3.
На рис. 3–4 представлена нормированная корреляционная функция полей деформаций для пористого материала с различным содержанием сферических пор ( р = 0,20 и р = 0,24). Нормирование проводилось делением значений построенной корреляционной функции на дисперсию полей деформаций, т.е. на корреляционную функцию при r - х| = 0. В качестве размеров r — х | используем условные единицы. Вид полученных моментных функций полей деформаций в целом схож с видом структурных моментных функций (см. рис. 2), поэтому для аппроксимации были протестированы те же исходные выражения (25), (26), что были использованы для аппроксимации структурных функций.
Проведено исследование моментной функции полей деформаций для структур с эллипсоидальными порами от объемного содержания (рис. 5) и от вариации разброса максимального размера полуоси эллипсоидальных включений (рис. 6).
Так как наибольшие значения корреляционной функции полей деформаций возникают при |r 1 - r 2| =0, а это дисперсии полей деформаций, то при решении краевой задачи в каких-то частных случаях достаточно учитывать только дисперсии для характеристики полей деформаций.
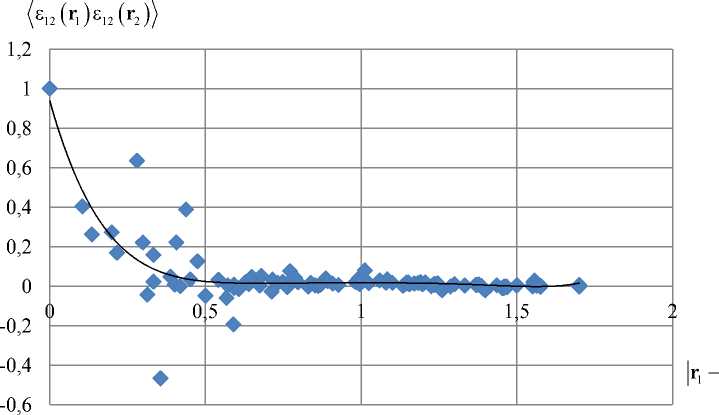
Рис. 3. Нормированная интерполированная моментная функция деформации ^812 (r1 )812 (r2) для структуры с объемной долей 20 % при чистом сдвиге; значения нормированной моментной функции деформаций; интерполированнаямоментнаяфункциядеформаций
Fig. 3. Normalized interpolated correlation function of strain ^8 12 ( r 1 ) 8 12 ( r 2 )^
for a structure with a volume fraction of 20 % at pure share; are values of normalized correlation function of strains; is interpolated correlation function of strains
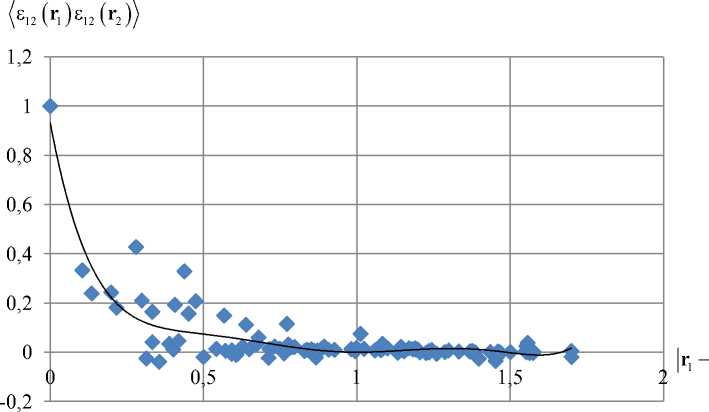
Рис. 4. Нормированная моментная функция деформации ^8 12 ( r 1 ) 8 12 ( r 2 )^
для структуры с объемной долей 24 % при чистом сдвиге; значения нормированной моментной функции деформаций; интерполированнаямоментнаяфункциядеформаций
Fig. 4. Normalized correlation function of strain ^812 (r1 )812 (r2 )) for a structure with a volume fraction of 24 % at pure share; are values of normalized correlation function of strains; is interpolated correlation function of strains
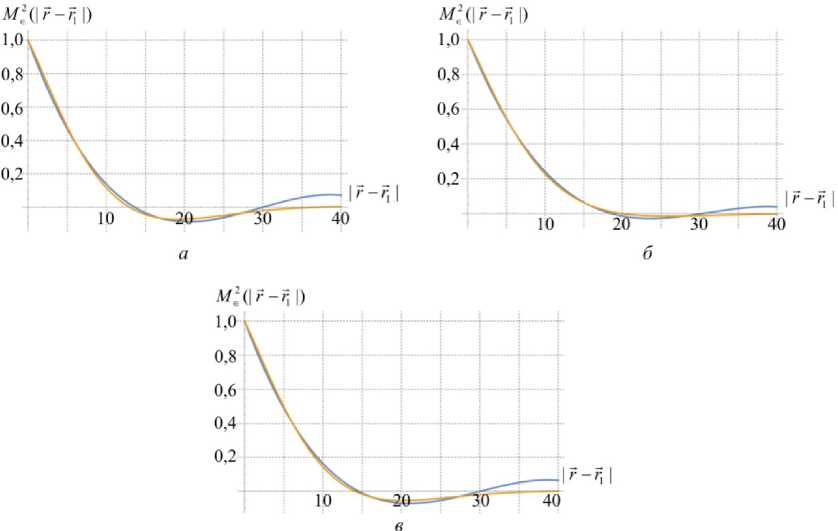
Рис. 5. Интерполированная () и аппроксимированная () моментные функции деформаций для структур с различным разбросом максимального размера полуоси эллипсоидальных включений: а – от 6 до 22; б – от 9 до 13; в – от 4 до 24 Fig. 5. Interpolated ( ) and approximated ( ) correlation function of strains for structures with a different range of maximum sizes of semi-axis ellipsoidal inclusions: а – is from 6 to 22; b – from 9 to 13; c – from 4 to 24
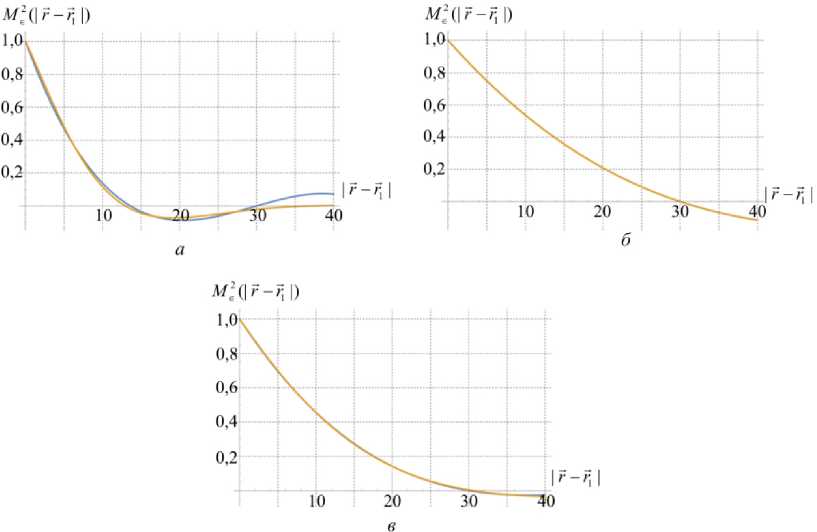
Рис. 6. Интерполированная () и аппроксимированная () моментные функции деформаций для структур с различной объемной долей включений: а – 4 %; б – 10 %; в – 13 %
Fig. 6. Interpolated ( ) andapproximated ( ) correlation function of strains for structures with a different range of volume fraction of inclusions: а – 4 %; b – 10 %; c – 13 %
В качестве примера решения упругопластической задачи был произведен расчет также для пористого материала с матрицей, обладающей следующими свойствами: модуль упрочнения G M = 44,2 ГПа, модуль сдвига G M = 14,3 ГПа, коэффициент объемного сжатия K M = 132,2 ГПа, j ^ 2) = 6,37 х 10 - 4. В качестве примера представлены моментные
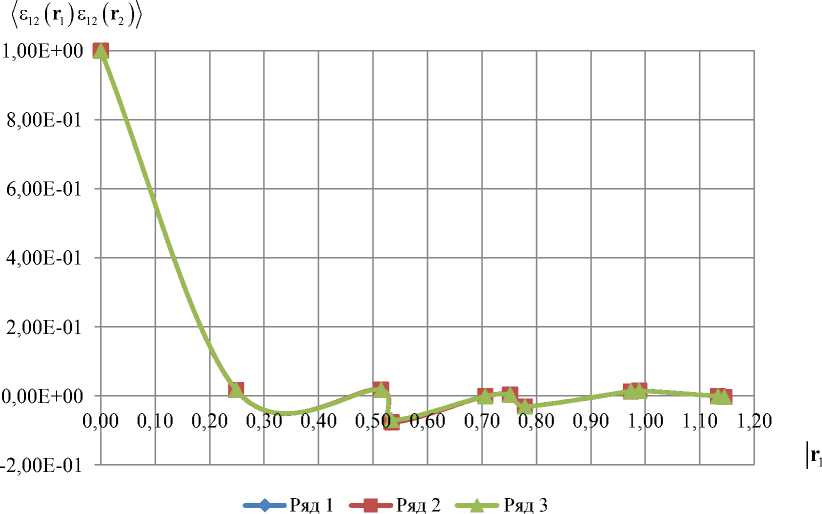
Рис. 7. Нормированные моментные функции полей деформаций в упругопластической задаче в разных точках деформирования для структур со сферическими включениями с разным объемным содержаниемр = 0,20; 0,24; 0,28 при (е12) = 2,25E - 04
Fig. 7. Normalized correlation functions of strain fields in an elastoplastic problem at different straining points for structures with spherical inclusions of different volume fractionsр = 0,20; 0,24; 0,28 at(е12) = 2,25E - 04
функции полей напряжений и деформаций. Проведено исследование в зависимости от объемной доли включений. Корреляционные функции полей деформаций для структур с содержанием пор от 15 до 28 % можно аппроксимировать одним выражением с одинаковыми константами (рис. 7)
Выводы
Были рассмотрены частные случаи представительных объемов многокомпонентных композитов со случайным расположением эллипсоидальных включений. Разработана и реализована методика вычисления значений корреляционных функций полей деформирования в упругом и упругопластическом случае при различных условиях нагружения и физико-механических характеристиках компонентов композитов. Для получения значений условных и безусловных корреляционных функций полей напряжений и деформаций в представительных объемах и их компонентах использовано решение стохастической краевой задачи в полном корреляционном приближении. В качестве входных параметров для вычислений выступают константы, характеризующие свойства компонентов предста- вительного объема, и входящие в функции Грина в подынтегральных выражениях, а также геометрические свойства компонентов и представительного объема, определяемые структурными моментными функциями.
Построены корреляционные функции напряжений и деформаций для разреженных структур со сферическими и эллипсоидальными полыми включениями. Проведено исследование и выбор аппроксимирующих зависимостей для полученных моментных функций. Полученные численные результаты могут использоватьсяв стохастических моделях для предсказания момента начала разрушения микроструктурных компонентов материала.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проекты16-41-590259 и 16-01-00682), а также гранта Президента Российской Федерации для государственной поддержки молодых российских ученых - кандидатов наук (проект МК-5172.2015.1).
Список литературы Корреляционные функции полей напряжений и деформаций в микронеоднородных средах
- Buryachenko V. Micromechanics of heterogeneous materials. -New York: Springer, 2007. -686 p.
- Rasool A., Böhm H.J. Effects of particle shape on the macroscopic and microscopic linear behaviors of particle reinforced composites//International Journal of Engineering Science. -2012. -Vol. 58. -P. 21-34 DOI: 10.1016/j.ijengsci.2012.03.022
- Mishnaevsky Jr. L., Derrien K., Baptiste D. Effect of microstructure of particle reinforced composites on the damage evolution: probabilistic and numerical analysis//Composites Science and Technolog. -2004. -Vol. 64. -Iss. 12. -P. 1805-1818 DOI: 10.1016/j.compscitech.2004.01.013
- Yu M., Zhu P., Ma Y. Effects of particle clustering on the tensile properties and failure mechanisms of hollow spheres filled syntactic foams: A numerical investigation by microstructure based modeling//Materials & Design. -2013. -Vol. 47. -P. 80-89 DOI: 10.1016/j.matdes.2012.12.004
- Torquato S. Random heterogenous materials, microstructure and macroscopic properties. -Springer, 2001. -701 p.
- Шермергор Т.Д. Теория упругости микронеоднородных сред. -М.: Наука, 1976. -400 с.
- Вильдеман В.Э., Соколкин Ю.В., Ташкинов А.А. Механика неупругого деформирования и разрушения композиционных материалов. -М.: Наука, 1997. -288 с.
- Волков С.Д., Ставров В.П. Статистическая механика композитных материалов. -Минск: Изд-во Белорус. гос. ун-та, 1978. -208 с.
- Ломакин В.А. Статистические задачи механики твердых деформируемых тел. -М.: Наука, 1970. -139 с.
- Ванин Г.А. Микромеханика композиционных материалов. -Киев: Наукова думка, 1985. -302 с.
- Beran M. J. Statistical continuum theories. -New-York: Wiley. Intersci. Publ., 1968. -493 p.
- Болотин В.В., Москаленко В.К К расчету макроскопических постоянных сильно изотропных композиционных материалов//Изв. АН СССР. Механика твердого тела. -1967. -№ 3. -С. 106-111.
- Хорошун Л.П. Методы случайных функций в задачах о макроскопических свойствах микронеоднородных сред//Прикл. механика. -1978. -Т. 14. -Вып. 2. -С. 3-17.
- Сараев Л.А., Глущенков В.С. Неупругие свойства многокомпонентных композитов со случайной структурой. -Самара: Самарский университет, 2004. -163 c.
- Ghossein E., Lévesque M. Homogenization models for predicting local field statistics in ellipsoidal particles reinforced composites: Comparisons and validations//International Journal of Solids and Structures. -2015. -Vol. 58. -P. 91-105 DOI: 10.1016/j.ijsolstr.2014.12.021
- Jiao Y., Stillinger F. H., Torquato S. Modeling heterogeneous materials via two-point correlation functions. II. Algorithmic details and applications//Physical Review. -2008. -Vol. 77. -No. 3. -P. 031135 DOI: 10.1103/PhysRevE.77.031135
- Computational microstructure characterization and reconstruction for stochastic multiscale material design/Yu. Liu, M. Steven Greene, W. Chen, D.A. Dikin, W.K. Liu//Computer-Aided Design. -2013. -Vol. 45. -P. 65-76 DOI: 10.1016/j.cad.2012.03.007
- Lee H., Gillman A.S., Matouš K. Computing overall elastic constants of polydisperse particulate composites from microtomographic data//Journal of the Mechanics and Physics of Solids. -2011. -Vol. 59. -Iss. 9. -P. 1838-1857 DOI: 10.1016/j.jmps.2011.05.010
- Берестова С.А., Хананов Ш.М. О некоторых путях становления структурно-феноменологических теорий в механике деформируемого твердого тела//Вестник Пермского национального исследовательского политехнического университета. Механика. -2010. -№ 4. -С. 17-28 DOI: 10.15593/perm.mech/2015.3.12
- Паньков А.А. Статистическая механика пьезокомпозитов. -Пермь: Изд-во Перм. гос. техн. ун-та, 2009. -480 с.
- Соколкин Ю.В., Ташкинов А.А. Механика деформирования и разрушения структурно-неоднородных тел. -М.: Наука, 1984. -116 с.
- Ташкинов М.А., Вильдеман В.Э., Михайлова Н.В. Метод последовательных приближений в стохастической краевой задаче теории упругости структурно-неоднородных сред//Механика композиционных материалов и конструкций. -2010. -Т. 16. -№ 3. -С. 369-384.
- Tashkinov M. Statistical characteristics of structural stochastic stress and strain fields in polydisperse heterogeneous solid media//Computational Materials Science. -2014. -Vol. 94. -P. 44-50 DOI: 10.1016/j.commatsci.2014.01.050
- Tashkinov M.A. Methods of Stochastic Mechanics for Characterization of Deformation in Randomly Reinforced Composite Materials//Eds. V.V. Silberschmidt, V.P. Matveenko. Mechanics of Advanced Materials. -Springer. -P. 43-78 DOI: 10.1007/978-3-319-17118-0_3
- Ташкинов М.А. Стохастическое моделирование процессов деформирования упругопластических композитов со случайным расположением включений с использованием моментных функций высоких порядков//Вестник Пермского национального исследовательского политехнического университета. Механика. -2014. -№ 3. -С. 163-185 DOI: 10.15593/perm.mech/2014.3.09
- Ташкинов М.А. Моделирование упругого поведения многокомпонентных композиционных материалов с использованием приближенных решений стохастических краевых задач//Вестник Пермского национального исследовательского политехнического университета. Механика. -2015. -№ 3. -С. 165-181 DOI: 10.15593/perm.mech/2015.3.12
- Ташкинов М.А. Статистические характеристики полей напряжений и деформаций в компонентах композитов со сферическими включениями при различных видах макрооднородного напряженно-деформированного состояния//Решение инженерных задач на высокопроизводительном вычислительном комплексе Пермского национального исследовательского политехнического университета: моногр./под ред. В.Я. Модорского. -Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2014. -C. 172-192.
- Соколкин Ю.В., Паньков А.А. Сингулярное приближение метода периодических составляющих для дисперсий деформаций в фазах композита//Механика композиционных материалов и конструкций. -2001. -Т. 7, № 4. -С. 427-433.
- Соколкин Ю.В., Ташкинов А.А. Механика деформирования и разрушения структурно неоднородных тел. -М.: Наука, 1984. -116 с.


