Корреляционный анализ по хозяйствам Орловского района

Автор: Курочкина И.А.

Журнал: Экономика и социум @ekonomika-socium

Статья в выпуске: 6-3 (19), 2015 года.

Бесплатный доступ

В данной статье представлен корреляционный анализ по хозяйствам Орловского района. Рассчитывается множественная корреляция, коэффициент эластичности, детерминации, коэффициент корреляции. Сделаны выводы по полученным показателям.

Короткий адрес: https://sciup.org/140115484

IDR: 140115484

Текст научной статьи Корреляционный анализ по хозяйствам Орловского района

Для глубокого исследования взаимосвязи социально-экономических явлений используется корреляционно-регрессионный анализ. Цель корреляционно-регрессионный анализа – установить, с каким из показателей, включённых в группировку, наиболее тесно связан группировочный признак.

Наметим показатели, которые будут включены в анализ при простой корреляции. Факторный признак – удой молока от 1 коровы, результативный

– окупаемость затрат.

Таблица 1 - Исходные данные корреляционно – регрессионного анализа по хозяйствам Орловского района.

Название предприятий	Производительность коров, ц Х	Окупаемость, % Y
ООО Авангард	22,0	107,5
ООО Звягинки	23,2	110,1
ООО Троицкое	21,9	95,9
ОАО ОПХ Красная Звезда	28,1	93,4
ЗАО Березки	23,2	81,2
ФГУП УПХ Лавровский	26,1	106,9
ООО Хлебороб	21,1	97,8
ООО Троицкое	22,8	94,4
ООО Орловские зори	23,4	85,0
ООО Фирма Ока	22,8	86,3
Итого	234,5	958,5
Ср. знач.	23,5	95,9

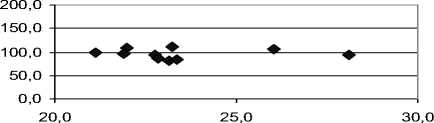
Установим форму связи между фактором и результатом. Для этого изобразим рисунок 1.

Ряд 1

Производительность коров, ц

Рисунок 1 - Зависимость между удоем молока от 1 коровы и окупаемостью затрат по предприятиям

Исходные данные показывают, что между удоем молока от 1 коровы и окупаемость затрат имеется в основном прямо пропорциональная зависимость, поэтому форму связи определим как линейную.

Подготовим данные для корреляционно – регрессионного анализа.

Таблица 2 - Расчетные данные корреляционно – регрессионного анализа.

Наименование предприятий	Производитель ность коров, ц Х	Окупаемость, % Y	X*X	Y*Y	X*Y
ООО Авангард	22,0	107,5	484,0	11551,2	2364,5
ООО Звягинки	23,2	110,1	539,5	12120,5	2557,2
ООО Троицкое	21,9	95,9	478,7	9198,3	2098,5
ОАО ОПХ Красная Звезда	28,1	93,4	789,5	8731,3	2625,5
ЗАО Березки	23,2	81,2	536,7	6590,9	1880,8
ФГУП УПХ Лавровский	26,1	106,9	678,8	11434,0	2786,0
ООО Хлебороб	21,1	97,8	446,4	9567,1	2066,5
ООО Троицкое	22,8	94,4	518,8	8902,8	2149,1
ООО Орловские зори	23,4	85,0	545,4	7219,4	1984,3
ООО Фирма Ока	22,8	86,3	521,4	7455,4	1971,5
Итого	234,5	958,5	5539,1	92771,1	22483,8
Ср. знач.	23,5	95,9	553,9	9277,1	2248,4

Определим тесноту связи между изучаемыми признаками, рассчитаем коэффициент корреляции.

σx =

Z x2

( x ) 2

; σx = 1,98; σy =

X y2

—

(y )2

; σy = 9,47;

xy — x • У r = ux uy ; r = 0,027 ; D = 0,07%

Построим уравнение регрессии и определим параметры уравнения:

y = a0 + alx; ^ y na⁰ ⁺ a ¹ ^Z x -55.93=10*a0+224.96*a1 a0= 92,84

£ xy = a о X ^x ⁺ a i ^£ ^x ² -401.61=224.96*a0+5178.37*a1 a1= 0,13

x ax • y=0,13*x+92,84; Э1 = y ; Э1= 22,75

Коэффициенты эластичности позволяют сказать следующее: при увеличении удоя молока на 1% окупаемость уменьшается на 22,75 пункта.

Проведенный нами расчет коэффициента корреляции показал, что между производительностью коров и окупаемостью затрат есть связь прямая, (r < 0,3). Коэффициент детерминации равный 0,07 % говорит о том, что на изменение окупаемости повлияла продуктивность коров, во всех других случаях на изменение окупаемости оказали влияние другие неучтенные факторы.

Корреляционное уравнение связи показывает, что окупаемость затрат изменяется в среднем на 0,13 % при повышении удоя молока на 1ц.

Показатель окупаемостью затрат связан не с одним, а с несколькими факторами, поэтому следует применить множественный корреляционный анализ. В качестве второго факторного признак возьмём трудоемкость 1ц продукции, чел.-час.

Подготовим данные для множественного корреляционнорегрессивного анализа (таблица 3).

Таблица 3 - Исходные данные для множественного корреляционно-регрессионнго анализа.

№ предприятий	Произв-ть коров, ц Х1	Трудоем кость 1ц, чел.-час. Х2	Окупаемост ь, % У	X1*X1	X2*X2	Y*Y	X1*X2	X1*Y	X2*Y
ООО Авангард	22,0	9,8	107,48	484	96,83	11551,2	216,483 5	2364,5	1057,6
ООО Звягинки	23,2	9,2	110,09	539,506 2	84,60	12120,5	213,636 4	2557,2	1012,6
ООО Троицкое	21,9	9,6	95,908	478,749 4	91,59	9198,3	209,401 7	2098,5	917,9
ОАО ОПХ Красная Звезда	28,1	10,2	93,441	789,460 8	104,78	8731,3	287,610 6	2625,5	956,5
ЗАО Березки	23,2	9,3	81,185	536,694 4	86,08	6590,9	214,942 5	1880,8	753,2
ФГУП УПХ Лавровский	26,1	8,2	106,93	678,813 7	67,16	11434,0	213,513 5	2786,0	876,3
ООО Хлебороб	21,1	11,5	97,812	446,378	131,80	9567,1	242,553 2	2066,5	1122,9
ООО Троицкое	22,8	11,3	94,355	518,760 6	126,90	8902,8	256,578 9	2149,1	1062,9
ООО Орловские	23,4	11,0	84,967	545,393 4	120,25	7219,4	256,097 6	1984,3	931,8

зори
ООО Фирма Ока	22,8	12,4	86,345	521,361 1	154,88	7455,4	284,166 7	1971,5	1074,6
Итого	234,5	102,5	958,5	5539	1064,88	92771,1	2395	22483,8	9766,2
Ср. знач.	23,5	10,2	95,9	554	106,49	9277,1	239	2248,4	976,6

В случае двухфакторной линейной регрессии уравнение связи имеет вид: Y = a0+a0 x1+a2 x2.

Рассч итаем парные и частные коэффициенты корреляции.

² 2 2 ²

J^ -(J )2 Л-(X 1 У -(x2 )

σy = ⁿ ; σx1 = ⁿ ; σx2 = ⁿ ;

xy - xy oy = 9,47; oxi = 1,98; ox2 = 9,47; r yx1 = °x1 *^ ; r yx1 = 0,027;

xy ^- x 2 y X 1 X 2 — X 1 X 2

r yx2 = & ^x ² * ^ y ; r yx2 = -0,487; r x1x2 = ^ x ¹ * ^a x ² ; r x1x2 = -0,341;

r - r r ryx1 ryx2 rx1x 2

r yx1(x2) = ^(1 ryx2 )(1 rx 1 x2); ryx1(x2) = -0,18 ; r yx2(x1) = r - r r ryx2 ryx1 rx1x 2

7⁽¹ ^- r yx 1 X^{1 -} r x 1 X 2 ) .

;

r yx2(x1) = - 0,54 ; r x1x2(y) =

r x 1 x 2 ^- r yx 1 * r yx 2

¹ ¹ ^- r x 1 1¹ ^- r x ² ) ; r x1x2(y) = -0,375;

r yx 1 + ryx 2 ^- ² * r yx 1 * r yx 2 * r x 1 x 2

R yx1x2 = ’ ¹ ^- r x2 x ² ; R yx1x2 = 0,51.

Определим параметры уравнения множественной регрессии.

° y '^(ryx 1 ^- r yx 2 * r x 1 x 2 )

^ y ■ ⁽ ^ryx 2 r yx 1 * ^rx 1 x 2 )

ai= ° x 1 . ( 1 ^- r x i x 2 ) ; a1 = -0,75; а2= ^a x 2 ⁽ ¹ ^- ^rx i x 2 ) ; a2 = -4,21;

a0 = ^y ^- a 1 ^x 1 ^- a ² ^x 2 ; a0 = 156,56; y = 156,56 — 0,75*x1 -4,21*x2

x а * ^

^y ; Э1= -0,184;

Определим коэффициенты эластичности: Э1 =

x а2

Э2= ^y Э2= - 0,45.

На этом основании можно сказать, что связь тесная и обратная по направлению возникает между результативным и факторным признаком х2 – трудоемкостью 1 ц молока, то есть при увеличении факторного признака результативный уменьшается (ryx2 = -0,487). Связь между результативным признаком и фактором х1 – удоем молока от 1 коровы – можно оценить как слабую и прямую (ryx1 = 0.027). Связь между факторными признаками умеренная и обратная. Наиболее тесная связь между х2 и у.

Совокупный коэффициент корреляции R yx1x2 показывает, что связь между признаками сильная.

Коэффициенты эластичности показывает, что при увеличении удоя молока на 1% окупаемость уменьшается на 0,18 пункта, в то время как увеличение трудоемкости на 1% влечёт уменьшение окупаемости на 0,45 пункта.

Таким образом, результативный признак наиболее тесно связан с фактором х2- трудоемкостью.

Список литературы Корреляционный анализ по хозяйствам Орловского района

Луценко А.И. Основы статистики сельского хозяйства. М: Финансы и статистика, 2013.
Минаков И.А. Экономика сельского хозяйства. М.: Колос С, 2009.
Яколвева Н.А. Корреляционный анализ прибыли предприятия агропромышленного комплекса//Сборник статей 2-ой Международной научной-практической конференции «Приоритеты системной модернизации России и ее регионов» (11 июня 2014 г.), Юго-Западный гос. Ун-т А.А. Горохов, Курск, 2014г.

Статья научная