Корреляционный метод поиска и координатометрии излучающего радиоэлектронного средства в заданном секторе

Рис. 1. Графическая постановка задачи

от пеленгаторов; θ1, θ2 – азимуты направления максимумов диаграмм направленностей антенн первого и второго пеленгаторов соответственно.

Существо триангуляционно-корреляционного местоопределения заключается в реализации синхронного по пространству и времени пеленгования источников излучения с последующей корреляционной обработкой потока сигналов от каждого из пеленгаторов в интересах выявления сигналов тех источников, координаты которых принадлежат априорно заданной «просматриваемой» области пространства [2–4]. Пространственно-временная синхронизация реализуется путем одновременного формирования диаграмм направленности пеленгаторов, максимумы которых ориентированы на геометрический центр просматриваемого элемента области поиска.

Выражения, определяющие вычислительный алгоритм управления диаграммами направ-ленностей пеленгаторов, представлены в следующем виде:

где

0 ₁ ' = arctg (

У о - У1 + j • dy

x0 - x1 + i • dx

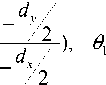
0/- a, 01 > a a - 0 ', 01' < a

0 2 ' = arctg (

d

Уо — y + j • dy — Ai

⁰           y ----42-7 ), 0 2

x - x0 + B - i • d + xA

¹⁰       x /2

02'+ a - n, 02' > n - a n - (a + 02'), 02' < n - a

i = 1, n -1, j = 1, m — 1, n = [Dr], m = [Dy1 ] dxdy

Следует отметить, что углы q1', q2' – величины, функционально зависящие от времени. Вид зависимости определяется выражениями (1) через параметры индексов элементов разрешения области поиска. В частности, j = Fy (t),  E{Fy (t)} = [1, m -1]

i = F x ( t ),   E { F x ( t )} = [1, n - 1]

Одной из основных особенностей формирования F_y ( t ) и F_x ( t ) помимо согласования их областей определения, что обеспечивает синхронизацию в изменении диаграмм направленностей (ДН) пеленгаторов, является реализация возможности функционального исключения элементов разрешения области поиска с наименее вероятным расположением излучающих РЭС.

Очевидно, что с каждого из направлений ориентирования ДН пеленгаторов будет формироваться поток сигналов, излучающих РЭС. Определение наличия в каждом из потоков сигнала одного и того же радиоэлектронного средства, что свидетельствует о его расположении в области пространства пересечения диаграмм направленностей, возможно за счет корреляционной обработки.

При работе источников излучения в непрерывном режиме значение корреляционной функции сигналов пеленгаторов будет определяться в следующем виде:

t + t

K ( t ', t , t ) = J X 1 ( t) x 2 ( t -1 ') dt

t

X i ( t ) = q S i x ^, y j ( t ) + E S m ( t ) + n 1 (t )

m

X 2 ( t ) = q S 2 x ‘ ’ y j ( t ) + E S k (t ) + n 2 ( t ) ,

k где q e[0,1] - случайный параметр различения; S^-^t) - реализация сигнала Sx(t) (искомого сигнала) на выходе первого и второго пеленгаторов соответственно; Sm(k) – сигналы, поступающие с фиксированных направлений пеленгования первого и второго пеленгаторов соответ-ственн0; ni(2)(t) - шум на выходе первого и второго пеленгаторов; m = 1,M; n = 1, N — количество сигналов в каждом из потоков; τ – интервал времени накопления.

В интересах решения задачи различения сигналов пороговый уровень принятия решения о наличии в реализациях сигнальных функций сигнала S ^{xi , yj} ( t ) целесообразно определить в соответствии с критерием идеального наблюдателя, предусматривающим минимизацию вероятности суммарной ошибки:

h opt = argmint P ^ ош ⁽ h )},

∞h где Pzош(h) =fР(K(t',tT)/9 = 0)dK(t',tт) + J p(K(t',tт)/9 = 1)dK(t',tт) [5]. h                                      -∞

Рассмотрим случай пеленгования РЭС, излучающих узкополосные сигналы, поступающие на вход каждого из пеленгаторов. В качестве математических моделей определим комплексные сигналы в виде

S 1 ( t ) = s m 1 ( t ) e ^{( m} ° t + « < t      = s m 1 ( t ) j 0

S2( t) = Sm 2( t) ej(^ t+^ t )+Фю) = Sm 2( t) eM t, где Sm1(t), Sm2(t) – комплексные амплитуды рассматриваемых сигналов пеленгаторов [6].

1*

Исходя из соотношения a ⁽ t ) • b ⁽ t ) = -^Re{ a ⁽ t ) • b ⁽ t ) ^J a ⁽ t ) • b ⁽ t ^)} , можно показать, что

K ( t \t , t ) = ¹ [Re J Ц( t ) S(t - t ') dt } + Re‘J S ( t ) S 2 ( t - t)dt }].

Интегрируя комплексные функции сигналов, получим:

I t                                                                  *                  *

f S ( t ) S ₂ ( t - t ') dt = S ¹ m ⁽ t ) S ² m ⁽ t ) [ e j⁽² w ^{0t +1V)} ( e j w ^{0 t} - 1)]

_t                       2 w ₀

.

J S ( t ) S 2 ( t - 1 ') dt = .S 1 m ( t ) . S 2 m ( t )t e ^- j ^{( w} 0 t ^{1 -A j} ) t

Следует отметить, что выражения (8) получены при ограничениях на динамику изменения огибающей сигналов и множителей угловой модуляции (ejj1(t),ejj2(t)), а именно dS1m(t) dt

« ₀, d^{S 2} m (t ) t e [ t , t + t ]                ^dt

« 0

t g [ t,t + t ]

d j 1 ( t ) dt

« ₀ d j 2 ( t ) t e [ t, t + t ]               ^dt

« 0

t g [ t,t + t ]

Подставляя (8) в (7), окончательно для корреляционной функции узкополосных сигналов получим:

K ⁽ t ', t , t ) = S 1 m S 2 m ^[ s^{m( W c t} ) siⁿ(^{2 w} 0 t ^{+ w} 0 t ^{+ w} 0 t '^{+ j} 1 ⁽ t ) ^{+ j} 2 ⁽ t ) ^{+ j} 01 ^{+ j} 02 ) ⁺

2       w 0                                                     (10)

+ t cos( w ₀ 1 '-A j )]

Введенные ограничения (9) позволяют произвести анализ корреляционной функции, положив j 1 ( t ) = j 1 = 0, j ₂( t ) = j 2 = 0, j ₀₁ = 0, j ₀₂ = 0, что не повлияет на закономерность ее поведения на множестве аргументов.

Таким образом,

K ( t ', t , t ) = S ^{1 m} S ^{2 m} [ ^{Sin( W 0} t ) sin(2 w ₀ 1 + w ₀ t + w ₀ 1 ') + 1 cos( w ₀ 1 ')].             (11)

• 2      w ₀

В соответствии с выражением (11) были получены графики зависимости K ( t ', t , t ) от времени задержки и интервала времени накопления применительно к сигналу с частотой f = 1 МГц (рис. 2).

Анализ представленных зависимостей свидетельствует о периодичности корреляционной функции, что объясняется гармоническим характером исходных сигналов. При этом в области – 1251 –

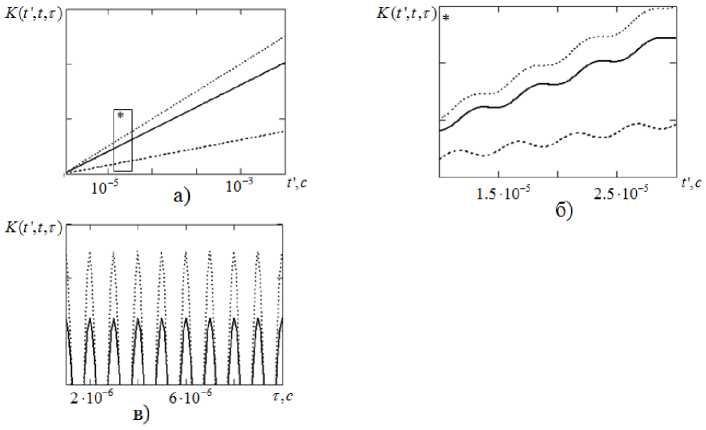
Рис. 2. Графики зависимости K ( t ', t , t ) от времени задержки сигналов и времени накопления

значений времени накопления период функции корреляции TK(ttt) = T0/2 (рис. 2б), в области значений времени задержки между сигналами TK(t‘ t,t) = T0 (рис. 2в). Следует отметить, что при больших значениях времени накопления по сравнению с длительностью периода функции (t >> T0) величина флуктуаций корреляционной функции значительно меньше ее средне го, так, при t / T0 = 100 и времени задержки, кратному T0 (t1 / T0 = n, n е □ )

K ( t ', t , t )

A K ( t ', t , t )

□ 1000

. Помимо этого, периодичность функции корреляции следует учитывать при анализе времени

(2^, n е □ - K ( t ', t , t ) = 0.

задержки сигналов пеленгаторов, в частности при t , / T 0 =

Таким образом, в статье рассмотрен метод определения местоположения источников радиоизлучения в заданном секторе поиска, основанный на триангуляционной координато-метрии с совместной корреляционной обработкой аддитивного потока сигнальных функций каждого из пеленгаторных постов, позволяющей реализовать режекцию входного потока электромагнитных контактов с ИРИ, тем самым повысить пропускную способность системы местоопределения и обеспечить поиск и анализ излучений в априорно заданном секторе поиска.