Ковалентное допирование нитрида углерода карбазолом и бензохалькодиазолами: моделирование электронных свойств в альтернативных приближениях

Нитрид углерода вызывает широкий интерес исследовательского сообщества благодаря простоте получения, привлекательной для многих практических целей электронной структуре, высокой физико-химической стабильности и доступности [1–3]. Графитоподобный нитрид углерода g-C 3 N 4 (ГНУ) в целом представляет собой плоскую двумерную структуру, которая в стабильной кристаллической форме не зафиксирована [4]. Разновидности ГНУ образованы триазиновыми или гептазиновыми звеньями. Наиболее энергетически выгодную структуру имеет мелем, представляющий собой гептазиновое звено. Мономеры мелема, связываясь между собой через атомы азота, образуют мелон [5], который является важным промежуточным продуктом при конденсации меламиновых колец до нитрида углерода [6].

Особый интерес представляет дальнейшая модификация сопряженной π-системы полигептазиновых цепей. Исследование органических полупроводниковых полимеров получило развитие в течение последних двух десятилетий, что привело к возникновению новой отрасли электронных устройств на основе органических светоизлучающих диодов, OLED, полевых транзисторов, OFET и органических фотогальванических элементов, OPV [7, 8]. Это развитие основано на модификации электронной структуры высокосопряженных органических полимеров. Основным подходом к этой модификации является введение донорных и акцепторных заместителей в полимерные цепи, которые нагнетают или отнимают электронную плотность в сопряженной системе, тем самым влияя на энергетические уровни и ширину запрещенной зоны полимера.

Хотя этот подход оказался эффективным при создании органической электроники, он мало применяется в синтезе фотокатализаторов для расщепления воды, окисления или разложения загрязняющих веществ из-за низкой стабильности и фотокоррозии [9, 10] Мы предлагаем применить донорно-акцепторный подход к ГНУ, который оправдан из-за его более высокой стабильности и надежности. Более того, убедительное количество публикаций однозначно указывает на положительное влияние молекулярного допирования и сополимеризации с g-C3N4 на фотокаталитическую активность. Исследована сополимеризация с производными бензола: п-фенилендиамин [11], тригидроксибензол [12], терефталевая кислота [13, 14], пиромеллитовый ангидрид [15–17], аминобензойная кислота [18], пиридины [19, 20], пиримидины [21–24], триазол [25], 3-аминотиофен-2-кабонитрил [9, 26, 27], фенилмочевина [28] и бензотиадиазол [29, 30].

Однако в большинстве этих публикаций изучается влияние одного допанта на активность ГНУ, что затрудняет полное понимание преобразования электронной структуры. Хотя в некоторых отчетах [31, 32] и показано влияние ряда допантов на фотокаталитическую активность по отношению к выделению водорода, сложно сделать вывод о природе возникающей эффективности катализа.

Полупроводниковые свойства ГНУ обусловлены делокализованной π-электронной структурой мелемовых или триазиновых субструктур, состоящих из атомов углерода и азота в sp2-гибридизации. С одной стороны, ароматическая π-система ГНУ в чистом виде содержит внутренние недостатки, с практической точки зрения, такие как быстрое рекомбинирование разделённых зарядов, неполное поглощение видимой части спектра, существенным образом сдерживающие её фотохимический потенциал [33, 34]. С другой стороны, на большом числе примеров было показано, что внедрение малых ароматических и гетероароматических молекул в полимерную структуру ГНУ способствует оптимизации запрещённой зоны полупроводниковых материалов, настройке уровней ВЗМО и НСМО, улучшению светочувствительности и фоторазделению зарядов [35].

Важным сдерживающим фактором для понимания особенностей взаимодействия ГНУ с допантами и механизмов его каталитической активности является недостаточность данных о структуре объектов исследований [36]. Первыми приближениями на пути к моделированию ГНУ являются его структурные звенья – меламин, мелем, димелем, мелон [37]. Такие звенья возможно успешно смоделировать в газофазном кластерном приближении с помощью различных методов и подходов, учитывая известный опыт [38–40]. Несмотря на невозможность учёта межзвенных взаимодействий, слоевых эффектов, на этом уровне моделирования удаётся корректно описать особенности, связанные со свойствами ковалентных связей, и в первом приближении учесть влияние атомных и молекулярных допантов типа пиридина на электронные характеристики [41]. Однако прогностические модели, позволяющие предсказать каталитическую активность ГНУ как его главное целевое свойство, требуют прямого учёта ближнего порядка и симметрии. Это становится возможным только при переходе к моделям с периодическими граничными условиями, позволяющим учесть двумерную или трёхмерную периодичность [42]. Рассмотрение таких моделей в литературе встречается намного реже, однако в числе наиболее выдающихся стоит отметить модели, в рамках ТФП, периодических расчётов с использованием локализованных атомных базисных наборов в CRYSTAL [43], а также сравнение различных подходов к вычислению ШЗЗ [44].

Все вышеперечисленные модели затрагивают вопросы построения двух- и трёхмерной структуры без точно известной геометрии взаимного расположения звеньев, а также позволяют получить ряд сопоставимых с расчётом электронных характеристик.

В представленном исследовании мы поставили следующие цели:

• •    моделирование молекул мелона, допированных рядом гетероциклов с выраженными электрон-донорными и электрон-акцепторными свойствами в 2 приближениях: кластерном и с периодическими граничными условиями;

• •    расчет электронных характеристик полученных систем, анализ взаимосвязи рассчитанных характеристик и имеющихся экспериментальных данных;

• •    определение влияния допантов на энергию связывания замещённого мелона с молекулой бензилового спирта;

• •    анализ результатов расчетов в 2 приближениях и разработка рекомендации по возможности использования методик расчетов для модификации свойств допированного мелона.

В работе представлены результаты моделирования структуры и свойств рассматриваемых π-электронных систем с экспериментальными данными на двух уровнях моделирования, а именно: 1) оптимизированные структуры и энергия граничных орбиталей для изолированных молекул мелона, состоящих из трех и девяти гептазиновых звеньев, полученные путем кластерного расчета молекулы в газофазном состоянии; 2) рассчитанная ширина запрещенной зоны для полимерных цепей мелона, смоделированных из девяти гептазиновых звеньев как мономеров, с периодическими граничными условиями. В обоих случаях одна молекула легирующей примеси соответствовала одной молекуле мелона или полимерному звену.

Экспериментальная часть

Серия анализируемых молекулярных структур мелона ( Tm_M ), ковалентно-связанного с замещенными гетероциклами на основе карбазола и 2,1,3-бензохалькодиазола ( 1–20 ), формировалась путем замещения атомов водорода и чередования молекулярных допантов, представленных молекулами с выраженными как электрон-донорными, так и электрон-акцепторными свойствами (табл. 1). Кластерные квантово-химические расчеты, включающие локализацию равновесной геометрии допированных структур мелона, были выполнены с использованием ТФП, в программе Gaussian 16 [45]. Были использованы функционалы с базисными наборами B3LYP/6-311+G(d,p) и HSE06/DZVP. Учет эффектов сольватации произведен методом поляризационного континуума То-маси, PCM [46]. Критерий сходимости по энергии 10^–8 ат. ед. и параметры по умолчанию уровня точности Tight. Выполнен расчет энергий граничных молекулярных орбиталей: высшей занятой (ВЗМО) и низшей свободной (НСМО), и разности граничных орбиталей, ΔE MO = Е НСМО – Е ВЗМО .

Таблица 1

Состав молекулярно-допированных структур мелона и энергии граничных орбиталей в кластерных расчётах, уровень расчета HSE06/DZVP

№	Обозначение	Электрон-акцепторный допант	Электрон-донорный допант	E ВЗМО , эВ	Е НСМО , эВ	ΔE MO , эВ
0	Tm_M	–	–	–6,32	–2,75	3,57
1	Tm_O	1,2,5-оксадиазол	–	–6,56	–3,09	3,46
2	Tm_S	1,2,5-тиадиазол	–	–6,49	–3,01	3,48
3	Tm_Se	1,2,5-селенадиазол	–	–6,47	–3,00	3,48
4	Tm_B_O	2,1,3-бензоксадиазол	–	–6,40	–3,16	3,23
5	Tm_B_S	2,1,3-бензотиадиазол	–	–6,23	–3,10	3,13
6	Tm_B_Se	2,1,3-бензоселенадиазол	–	–6,13	–3,20	2,93
7	Tm_D	–	карбазол	–5,64	–2,66	2,98
8	Tm_D_S	–	дибензотиофен	–5,90	–2,74	3,16
9	Tm_O_D	1,2,5-оксадиазол	карбазол	–5,75	–2,95	2,80
10	Tm_S_D	1,2,5-тиадиазол	карбазол	–5,72	–2,88	2,84
11	Tm_Se_D	1,2,5-селенадиазол	карбазол	–5,71	–2,87	2,85
12	Tm_B_O_D	2,1,3-бензоксадиазол	карбазол	–5,72	–3,08	2,64
13	Tm_B_S_D	2,1,3-бензотиадиазол	карбазол	–5,69	–3,03	2,65
14	Tm_B_Se_D	2,1,3-бензоселенадиазол	карбазол	–5,68	–3,14	2,53
15	Tm_O_D_S	1,2,5-оксадиазол	дибензотиофен	–6,00	–3,02	2,99
16	Tm_S_D_S	1,2,5-тиадиазол	дибензотиофен	–5,97	–2,94	3,03
17	Tm_Se_D_S	1,2,5-селенадиазол	дибензотиофен	–5,96	–2,93	3,04
18	Tm_B_O_D_S	2,1,3-бензоксадиазол	дибензотиофен	–5,97	–3,12	2,85
19	Tm_B_S_D_S	2,1,3-бензотиадиазол	дибензотиофен	–5,94	–3,07	2,87
20	Tm_B_Se_D_S	2,1,3-бензоселенадиазол	дибензотиофен	–5,93	–3,18	2,75

Локализация равновесной геометрии одномерных полимерных структур 8 исследуемых образцов производилась с помощью программного пакета CRYSTAL17 [47] методом ТФП с периодическими граничными условиями следующим образом. В качестве мономерного звена взята молекула, состоящая из трёх параллельных трёхзвенных молекул мелона, соединённых между собой в шахматном порядке. То есть одно звено моделируемого полимера состояло из 9 соединённых между собой в три ряда молекул мелема. Затем один или два атома водорода на краях мономерного звена замещались на молекулярные фрагменты допантов в нескольких сочетаниях. Информация о мономерных звеньях, использованных для моделирования соответствующих полимеров, приведена в табл. 2. Было установлено, что применение к моделированию того же уровня расчёта, что и для молекулярных структур, а именно B3LYP/6-311+G(d,p), даёт завышенные и далёкие от экспериментальных [48] значения ШЗЗ. Поэтому для локализации равновесной геометрии полимеров был использован уровень расчёта HSE06/pob-DZVP_rev2 [49, 50], давший более близкие к эксперименту значения ШЗЗ для незамещённого полимера. Для релаксации как исходной структуры мелона, так и замещённых полимеров использована опция POLYMER программного пакета CRYSTAL17 и следующие значения параметров программы: TOLDEG 0.00001, TOLDEX 0.00003, TOLDEE 10, TOLINTEG 14 14 14 14 24. Полученные значения ШЗЗ приведены в табл. 2.

Таблица 2

Состав молекулярно-допированных структур мелона в расчётах полимеров, значения ШЗЗ и разности энергий граничных орбиталей для соответствующих молекул

№	Обозначение	Допанты	Структура	ШЗЗ, эВ	ΔEMO, эВ
1	Tm_M	–		2,91 (2,56)*, (2,70)**	3,57
2	Tm_B_Se	2,1,3-бензоселенадиазол		2,72 (1,88)*	2,93
3	Tm_D	карбазол		2,26	2,98
4	Tm_B_Se_D	2,1,3-бензоселенадиазол, карбазол		2,49	2,53
5	Tm_B_O	2,1,3-бензоксадиазол		2,92 (2,41)*	3,23
6	Tm_B_S	2,1,3-бензотиадиазол		2,69 (2,00)*	3,13
7	Tm_B_S_D	2,1,3-бензотиадиазол, карбазол		2,45	2,65
8	Tm_B_O_D	2,1,3-бензоксадиазол, карбазол		2,60	2,64

Экспериментальное значение ШЗЗ [36]; ** Экспериментальное значение ШЗЗ [54].

Ан а л и з хара к тера в за и мод ействия в комплексах из молекулы ГНУ и б е н зи лов ого спирта п рои зв од и лся при п омощи ра счё т ов э н е рги и в з аимоде й с тв ия (E int ) молекул бензилового спирта и терм и н а л и з ов а н н ого фр агме н та н и три да у гле р од а. Р а сче т E int произведен методом противовеса, с у че том оши б к и с у п е рп ози ци и ба зи с н ого наб о ра п о фо рм у л е : E int = E AB – (E A + E B ) – E BSSE , где E AB – эн ергия м ол е к у лярн ого комплекса бензилового спирта и фрагмента н и три д а у глерод а, E A – эн ергия мол е к у лы бе н зил ов ого с п ирта , E B – энергия фрагмента нитрида углерода, E BSSE – п оп ра в к а н а ош и бк у с у перп оз и ц и и б а зи с н о го н а бора [ 51]. Расчет энергии нековалентных взаимодействий E HB п рои зве де н по уравнению Эспиноза с соавторами [ 52]: E HB = ΣE i,HB , E i,HB = 0,5υ(r b ), где E i,HB – эн ерги я отдельно взятого нековалентного взаимоде й с тв и я в к омп л е к се, υ(r_b) – п л отн ос ть п оте н ц и альн ой э н е рги и в связевой критической точке (3,–1) этого взаимодейст в и я. Р а с чет вы п олн е н в програ мме Gaussian 16 [45], критерий сходимости по э нерги и 10^–8 ат. ед. и п а раме тры п о у м ол ча ни ю у ро вня точности Tight. Визуализация и анализ ра сс чи та н н ых с т руктур молекул, пол и м еров, к омпл ексов и их молекулярных орбиталей выполнены п ри п омощ и п рограммы ChemCraft 1.8 [53].

Обсуждение результатов

Моле ку ля р ный дизай н к ов але нтн о -допированных соединений мелона

Для мод е ли р ов а н и я и золи рованных молекул мелона и их допированных п ро изводных были в ы б ра н ы ф ра гм е н ты, с остоящ и е из трех и девяти гептазиновых звеньев, из н а ча льн о и ме ющ ие п л ос к у ю с тру к ту ру. Рас п олож е н ие донорных и акцепторных гетероциклов в Г НУ в ыб ра н о с у ч е том и ме ющ и хс я э кс п е риме н та л ьн ых данных [36]. Разности энергий граничных молекулярных орбиталей ( ΔE MO ) д ля и золи рованных молекул мелона, замещенных од н и м и з бе н-зо[c ][1, 2, 5]ха л ьк о ге н ад и азолов , и оценки ШЗЗ для полимерных цепей тех ж е фрагме н тов , п олу ч е н ны е с п е ри о д и че ск и м и гра н и чными условиями, приведены в табл. 2. Также м ож но отметить, ч т о м ол ьн ое с оотн оше н и е молекулы допанта и мелона (в пересчете на мела ми н) в п оли ме рн о м зв е н е при ме рн о соответс т в уе т 5%-ному допированию в эксперименте. Этот факт позволяет срав н и ть э к с п е ри м е н та льные и ра с че тные э ле к трон ные харак те рис ти к и д оп и рованной молекулы ме- л он а , и х те нд е н ц и и и оц ени ть в озможные структурные особенности допирова н н ого мелон а .

С п е ц и фи че ск ое ра с поло же н ие допирующих заместителей повлияло на п рос транственн у ю структуру смоделированных сое д и не н и й ( ри с . 1 ) . Э лек трон-акцепторные допанты на основе 2,1,3- б е н зоха льк о д и а золо в могу т замещать атом Н первичной аминогруппы, т. е. располагаться в о д н ой из в е ршин гептаз и н ов ого к ольца Tm_M, находясь при этом в одной плоскости со связан н ы м ге п та зи нов ы м фрагментом ме л он а . Пл а н а рн ое ра с п оло же н и е этих фрагментов связано с эф ф е к т а ми с оп ря же н и я межд у д опантами и гептазиновым кольцом, которое по д к ре пле н о в озмо ж н ы м об ра зов а н и е м в о д ор од н ых с в язе й N…H–C. Электрон-донорные гетероциклы, замещающие по з ици и пр и вт о рич но м ат о м е азо т а м еж д у дв умя гепт аз ино вы ми кольцами, как правило, разверну т ы о р т о г о нал ь но по о т ношению к плоскости мелона. Молекулы мелона, допир о ванны е т ол ь ко электрон-акцепт о р ны ми зам ест ителями, содержащими в своей структуре хал ь ко г ены (O, S, Se), более планарны в случае Se как г ет ер о ат о м а в до пантах. Степень планарности мы определяли, как м аксим ал ь но е о т кл о нение ат о м о в, вх о д я щих в сост а в м ел о на, по ко о рдинат е Z от плоскости XY.

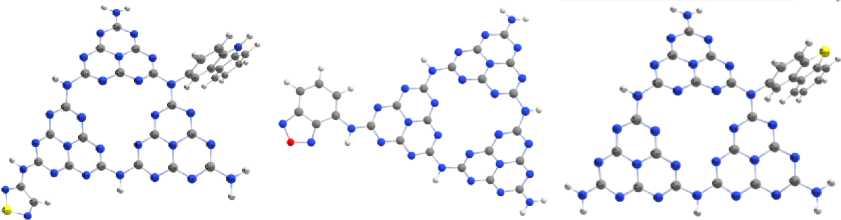
а)                                             б)                                 в)

Рис. 1. Примеры оптимизированных допированных структур мелона: а) Tm_S_D: акцептор – 1,2,5-тиадиазол, донор – карбазол, б) Tm_B_О: акцептор – 2,1,3-бензоксадиазол, в) Tm_D_S: донор – дибензотиофен

Например, для чистого Tm_M степень планарности составляет 2 , 37 Å. Молекулярное допирование чаще всего приводит к увеличению степени планарности в интервале 0 , 1–1 , 9 Å. Модели допированного мелона, построенные с учетом влияния растворителя, имеют более плоскую структуру, степень планарности уменьшается в среднем на 0 , 08 Å.

Рассмотрим изменение энергетических уровней ВЗМО и НСМО (рис. 2 и табл. 1) при модификации структуры мелона ковалентно-связанными допантами, а также разность граничных орбиталей (ΔE MO = Е НСМО – Е ВЗМО ). На рис. 2 видно, что модификация структуры любыми допантами закономерно влияет на изменение Е ВЗМО . Все значения энергий далее приведены относительно Е ВЗМО недопированного мелона, равной –6,32 эВ. Введение только электрон-донорных молекул повышает Е ВЗМО на 0,43…0,68 эВ, в среднем на 0,55 эВ. Одновременное присоединение к мелону электрон-донорных и электрон-акцепторных молекул приводит к повышению Е ВЗМО в среднем на 0,48 эВ. При введении только акцепторных молекул, больший вклад в изменение Е ВЗМО вносит атомная орбиталь более электроотрицательного атома. Поэтому для допантов, содержащих атом О, наблюдаемое изменение уровня ВЗМО сильнее, чем для соединений, содержащих атомы S и Se. Введение электрон-акцепторных молекул, представленных серией 1,2,5-халькогендиазолов, понижает значение Е ВЗМО на 0,15…0,24 эВ.

Рис. 2. Распределение значений энергий граничных орбиталей Е ВЗМО , Е НСМО в зависимости от состава и характера замещения атомов H в мелоне

Простой количественной зависимости изменения энергии НСМО от состава, положения и количества вводимых допантов не обнаружено (см. рис. 2). Максимальное понижение Е НСМО наблюдается для структуры, допированной только одним электрон-акцепторным допантом – 2,1,3-бензоселенадиазолом. Для структур, допированных дибензотиофеном и карбазолом, наблюдается незначительное повышение Е НСМО , на 0,05 эВ.

Анализ разности энергий граничных орбиталей ΔE MO показывает зависимость её значений от вида и количества вводимых допантов (рис. 3). Расчетное значение ΔE_MO для мелона Tm_M составляет 3,57 эВ. Отметим, что близкий результат (3,88 эВ) был получен в теоретических расчетах, опубликованных ранее [48]. В целом величина разности энергий ВЗМО и НСМО уменьшалась при введении любых исследованных допантов. Максимальное уменьшение ΔE_MO отмечается для структур, допированных одновременно и электрон-донорными, и электрон-акцепторными молекулами. Так, присутствие фрагментов 2,1,3-бензоселенадиазола и карбазола уменьшает ΔE MO на 1,04 эВ по сравнению с Tm_M. Введение только одного из этих допантов уменьшает ΔE MO максимально на 0,6 эВ.

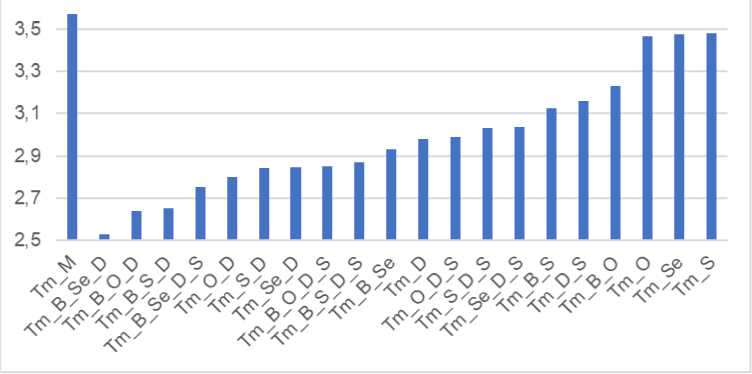
Рис. 3. Разность энергии граничных орбиталей ΔE MO , для структур с разными видами и количеством допантов

Анализ распределения электр онной плотности по молекулярным орбитал ям

Ковалентное допирование м елона только акцептирующими электронну ю плотность бенз о- халькодиазолами приводит к смещению локализации ВЗМО в основном на акцептор (рис. 4). НСМО имеет большую площадь распределения, локализуясь одновременно и на фрагменте а к цептора, и на связанном с акцеп тором гептазиновом кольце. Допирование к арбазолом как эле к-трон- донорной молекулой приводит к локализации ВЗМ О на донорном фрагменте молекулы, при этом НСМО локализована на мелоне (рис. 5).

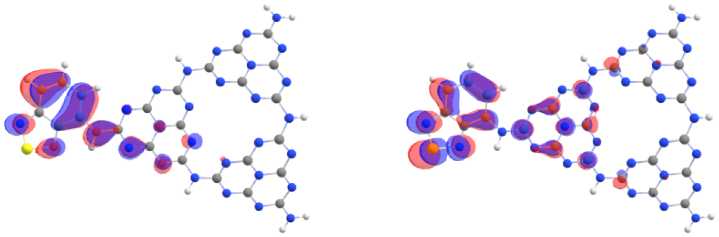
а)

б)

Рис. 4. Локализация ВЗМО (а) и НСМО (б) на молекуле мелона, допированной 2,1,3-бензотиадиазолом

Одновременное допирование донорными и акцепторными молекулами, наиболее эффектив но уменьшающее разность грани чных молекулярных орбиталей, приводит к одинаковой закон омерности: ВЗМО оста ется локализованной на электрон -донорном фрагменте, а НСМО локализуется на электрон- акцепторном фрагменте и связанном с ним гептазиновом кольце (рис. 6). Говоря более конкретно, показано, что ВЗМО допированного мелона преимущест венно локализована на атоме N и распределена на связях С –С молекулы карбазола, а НСМО локализована на атомах N халькогенсодержащих эле ктрон -акцепторных допантов, связанных с гептазиновым фрагментом.

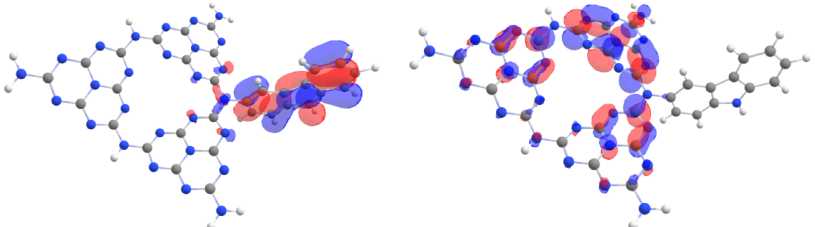
а)

б)

Рис. 5. Локализация ВЗМО (а) и НСМО (б) на молекуле мелона, допированной карбазолом

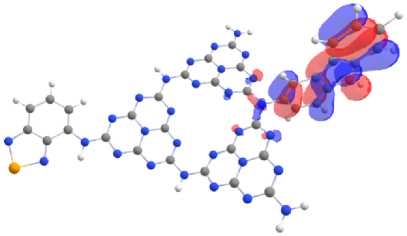
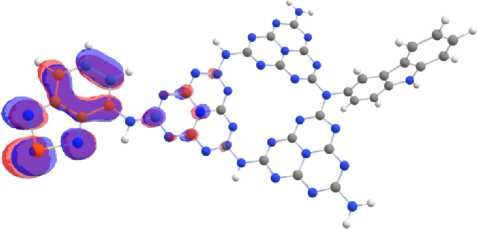
а)                                                                    б)

Рис. 6. Локализация ВЗМО (а) и НСМО (б) на молекуле мелона, допированной молекулами 2,1,3-бензоселенадиазола и карбазола

В целом стоит отметить, что введение допантов в структуру мелона приводит не только к уменьшению ΔEMO, но и к изменению локализации ВЗМО и НСМО в структуре молекулы. Это может способствовать образованию сайтов связывания на поверхности допированной молекулы по отношению к наиболее способным к сорбции модельным молекулам. Так, были исследованы взаимодействия в комплексах, состоящих из бензилового спирта и мелона, которые являются переходными в реакциях окисления бензиловых спиртов до альдегидов с использованием фотокатализатора.

Нековалентные взаимодействия в комплексах ГНУ с молекулой бензилового спирта

Рассмотрим нековалентные взаимодействия в комплексах, образованных молекулами допи-рованного мелона и бензилового спирта ( табл . 3), и оценим прочность связывания в комплексе, используя топологические характеристики электронной плотности [55] в критических точках связи в зависимости от вида допанта. При моделировании наблюдается, что молекула бензилового спирта, как правило, ориентируется практически параллельно псевдоплоскости допированного мелона и формирует несколько связевых путей, определяемых нековалентными взаимодействиями (рис. 7). Значения электронной плотности в критических точках нековалентных связей показывают, что наиболее сильное взаимодействие наблюдается для водородной связи О–H…N–C, образованной атомом Н в молекуле спирта и вторичным атомом N в гептазиновом фрагменте.

Таблица 3

Смоделированные комплексы молекулярно-допированных структур мелона с бензиловым спиртом, энергии взаимодействия молекул E int и энергии водородных связей E НВ в соответствующих комплексах

№	Обозначение	Структура	Eint, ккал/моль	EНВ, ккал/моль
1	Tm_M		–7,32	–3,92
2	Tm_B_Se		–7,22	–3,84
3	Tm_D	^^^^?	–7,44	–3,94

Окончание табл. 3

№	Обозначение	Структура	E int , ккал/моль	E НВ , ккал/моль
4	Tm_B_Se_D	V*frVv5»?r	–7,22	–3,99
5	Tm_B_O	^^^Vvy*^**^'	–7,47	–3,87
6	Tm_B_S		–7,37	–3,83
7	Tm_B_S_D	^«*v^£у/ V-	–7,43	–3,93
8	Tm_B_O_D		–7,75	–3,98

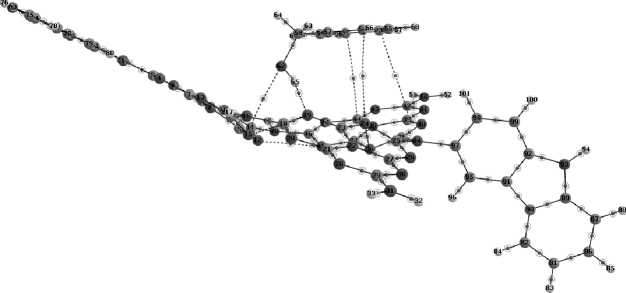
Рис. 7. Формирование связевых путей в комплексе между бензиловым спиртом и молекулой допированного мелона

Энергия взаимодействия молекул в комплексе Eint сравнивалась с энергией водородной связи EНВ, определяемой исходя из корреляции, предложенной Эспиноза с соавт. в работе [52]. Определенное отсутствие количественной корреляции энергии взаимодействия в 8 исследованных комплексах бензилового спирта и допированного мелона с энергией водородной связи говорит о том, что не только одна водородная связь О–H…N–C определяет прочность связывания молекул бензилового спирта на поверхности допированного мелона в молекулярных комплексах. По- этому нами также проведен анализ зависимости энергии взаимодействия от ЕВЗМО допированного мелона. Для комплексов, допированных карбазолом (рис. 8), с ростом ЕВЗМО энергия взаимодействия Eint меняется сильнее по сравнению с комплексами, допированными только акцепторными заместителями. В последних при повышении ЕВЗМО на 0,33 эВ энергия взаимодействия повышается на 0,25 ккал/моль.

При допировании мелона карбазолом наблюдается иная тенденция: при незначительном увеличении Е ВЗМО – на 0,02 эВ – E int увеличивается на 0,53 ккал/моль. Селенсодержащие комплексы имеют меньшие значения E int , чем комплексы с S и O. Установленная зависимость косвенно указывает на то, что нитрид углерода в образуемом комплексе с бензиловым спиртом выступает донором электронной плотности. Отмечено, что формирование более прочных комплексов может препятствовать частичному окислению спиртов. В случае допирования мелона электрон-акцепторными селенсодержащими структурами образуется промежуточный комплекс с менее прочными связями, чем с серой и кислородом, и поэтому окисление проходит более эффективно.

-7,1

-7,2

-7,3

8 -7,4

-7,5

-7,6

-7,7

-7,8

Tm_B_Se                     Tm_B_Se_D

Tm_M

Tm_B_S

Tm_B_S_D Tm_D

Tm_B_O

Tm_B_O_D

-6,7      -6,6      -6,5      -6,4      -6,3      -6,2      -6,1       -6,0      -5,9      -5,8

ЕВЗМО, эВ

Рис. 8. Зависимость энергии взаимодействия молекул бензилового спирта и ГНУ E int в комплексе от Е ВЗМО мелона и его допированных производных

Характеристики одномерных периодических моделей допированного мелона

Далее мы рассмотрим 1D-полимерные модели допированного мелона, полученные с использованием периодических граничных условий, и сравним значения ширины запрещенной зоны, рассчитанные для этих полимерных структур, и величины разности энергий граничных орбиталей ΔE MO , полученные для молекулярных моделей (рис. 9, см. табл. 2). Из указанного сравнения можно оценить, насколько может быть корректен переход от газофазного кластерного расчёта к расчёту с периодическими граничными условиями и насколько полученные значения при этом переходе приближаются к экспериментальным. Значение ШЗЗ для немодифицированного полимерного мелона, равное 2,91 эВ, оказывается значительно ближе к экспериментальному (2,7 эВ, [54]), чем ΔE MO , равное 3,57 эВ, которое рассчитано для газофазного состояния. Здесь, однако, следует отметить, что расчёт равновесной геометрии полимерного мелона с необходимыми параметрами требует на порядки б о льших компьютерных ресурсов и времени, чем расчёт фрагмента мелона в газофазном состоянии.

Тем не менее, как видно из обобщающего рис. 9, прослеживается некоторая зависимость между значениями ШЗЗ и ΔE MO . Мелон, допированный кислородсодержащими гетероциклами, имеет большее значение ШЗЗ и ΔE MO . Селенсодержащие допанты, наоборот, максимально уменьшают значения ШЗЗ и ΔE_MO. Однако корреляция этих значений в ряду меняющихся в допантах халькогенов (O, S, Se) низкая.

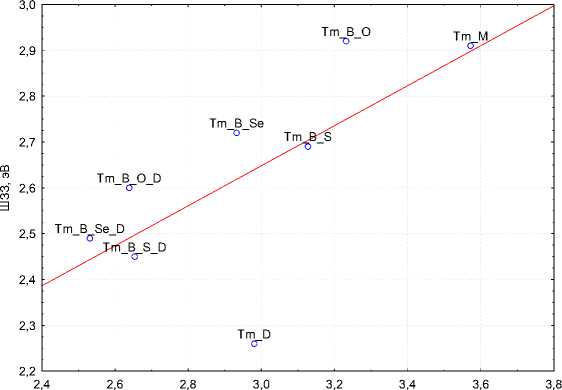
ΔE MO , эΒ

Рис. 9. Зависимость между значениями ШЗЗ и ΔE MO для исследуемых молекул

Из сравнения результатов расчётов в разных приближениях мы не можем сказать однозначно, какое допирование необходимо выполнить для максимального уменьшения ШЗЗ, так как при кластерном расчете наименьшую ΔE MO показывает мелон, допированный карбазолом и 2,1,3-бензоселенадиазолом. При периодических расчетах наименьшая ШЗЗ у мелона, допированного только электрон-донорной молекулой – карбазолом, затем следуют молекулы, допированные карбазолом и 2,1,3-бензотиадиазолом, карбазолом и 2,1,3-бензоселенадиазолом. Причем разница между ШЗЗ в двух последних случаях составляет 0,04 эВ. По рис. 9 также видно, что допирование мелона 2,1,3-бензоксадиазолом, по сравнению с другими допантами этого ряда, увеличивает ШЗЗ, даже по сравнению с недопированным мелоном.

Сравнение экспериментальных значений ШЗЗ и рассчитанных электронных свойств для ряда рассчитанных комплексов (табл. 4) показало следующее. При 5 %-ном допировании нитрида углерода бензо[c][1,2,5]халькогенадиазолами рассчитанные значения ШЗЗ и ΔE MO коррелируют с экспериментально измеренными значениями ШЗЗ 5% с коэффициентами 89 и 84 % соответственно (см. табл. 4). Изменение метода и уровня молекулярного расчета влияет на значения ΔE MO , при этом корреляция уменьшилась на 10 % при использовании метода учёта растворителя PCM и уровня HSE06/DZVP. Значения ШЗЗ и ΔE MO , полученные на уровне B3LYP/6-311+G(d,p), всегда имеют более высокое значение, чем для уровня HSE06/DZVP. Рассчитанное значение ШЗЗ для исходного ГНУ, равное 2,91 эВ, намного ближе к экспериментальным значениям 2,56 эВ [36] и 2,70 эВ [54], чем ΔE MO , рассчитанное для молекулы ГНУ в газофазном состоянии и равное 3,57 эВ.

Таблица 4

Экспериментальные и расчетные значения ШЗЗ и ΔE MO для исследуемых систем с электрон-акцепторными допантами

Обозначение	ΔEMO, эВ	EВЗМО, эВ	Е НСМО , эВ	ШЗЗ, эВ	E(TVB*), эВ	E(BVB*), эВ	ШЗЗ 5% , эВ
Tm_M	3,57	–6,32	–2,75	2,91	–5,72	–2,81	2,56 (2,70)
Tm_B_O	3,23	–6,40	–3,16	2,92	–5,72	–2,80	2,41
Tm_B_S	3,13	–6,23	–3,10	2,69	–5,65	–2,96	2,00
Tm_B_Se	2,93	–6,13	–3,20	2,72	–5,65	–2,93	1,88

* – TVB – верхний валентный уровень, BVB – нижний виртуальный уровень.

Учитывая вышеизложенное, мы можем отметить, что результаты, полученные на обоих расчетных уровнях, приемлемо соответствуют экспериментальным данным, а именно тенденциям изменения ширины запрещенной зоны при допировании исходной структуры ГНУ электрон-акцепторными молекулами. В то же время, моделирование полимера с периодическими граничными условиями позволяет рассчитать эти значения и их тренды при допировании различными бензо[c][1,2,5]халькогенадиазолами несколько ближе к самим экспериментальным значениям и, возможно, правильно предсказать их для других электрон-акцепторных заместителей. С другой стороны, расчет равновесной геометрии полимера ГНУ требует на порядки больше компьютерных ресурсов и времени, чем расчет геометрии молекулы ГНУ в газофазном состоянии.

Заключение

Проведено моделирование структур мелона, допированного рядом гетероциклических молекул с выраженными электрон-донорными и электрон-акцепторными свойствами, в 2-х приближениях. Во-первых, мы применили подход, основанный на расчетах изолированных молекул. Во-вторых, мы использовали периодические граничные условия для моделирования 1D полимерных цепей. Сравнивая рассчитанные значения ШЗЗ и ΔE_MO с экспериментальными данными для исходного и допированного ГНУ, мы пришли к выводу, что газофазные молекулярные расчеты больше подходят для качественной оценки трендов ΔE MO . Расчеты же полимерных цепей с периодическими граничными условиями дают удовлетворительные количественные зависимости ШЗЗ от вида и количества вводимого допанта. Одновременное допирование мелона электрон-донорными молекулами карбазола и электрон-акцепторными молекулами 2,1,3-бензохалькодиазолов максимально уменьшает разность энергий граничных орбиталей, а допирование только карбазолом максимально снижает ширину запрещенной зоны в рассмотренном ряду соединений.

Анализ распределения молекулярных орбиталей показал, что при эффективном допировании, максимально сужающем ΔE MO, ВЗМО локализовано на электрон-донорном фрагменте молекулы, а НСМО – на электрон-акцепторном фрагменте молекулы, что способствует быстрому рекомбинированию разделенных зарядов.

Допированные структуры ГНУ способны к образованию комплексов с бензиловым спиртом, образуемых за счет разных видов нековалентных взаимодействий. Селенсодержащие допанты ГНУ являются более подходящими молекулами для модификации катализатора в реакциях частичного окисления бензиловых спиртов.