Краевая задача несимметричной деформации цилиндрического резервуара с жидкостью в температурном поле

PNRPU MECHANICS BULLETIN

We framed a precise solution of the nonsymmetrical boundary value problem of the elasticity theory for a cylindrical vessel with liquid placed in the thermal field. The thermoelastic problem is unlinked, i.e. at first we solve the thermal conductivity equation, and then the linear problem of the elasticity theory for a circular cylinder in displacements.

It should be noted that until the present time there were no precise solutions of non-symmetrical problems of the elasticity theory in the cylindrical coordinate system with a consideration of the thermal field. It is explained by the complexity of the system of resolvent equations, such as high order, variable coefficients. The authors of the article managed to form integrable combinations of resolvent equations in this work, at first by taking no account and then considering the thermal fields. For this purpose an additional equation related to a volumetric deformation was introduced into the system of resolvent equations instead of the relator connecting the volumetric deformation with the movement of the cylinder points. When we took into account the heat conduction equation, we managed to gain the equation which had been obtained earlier without the consideration of the thermal elements. As a result, the problem was brought to a successive solution of each equation separately. Since the additional equation was obtained by the derivation of the rest of the equations, the order of the resolvent equations system became higher which resulted in «excess» constants of the integration. The authors proved that the use of the replaced correlation between the volumetric deformation and displacements as an additional condition eliminated this disadvantage.

We formed a precise solution of the boundary value problem for the cylindrical vessel with liquid upon the condition of the linear dependence of temperature and displacements of the cylinder along its axis. The numerical example was considered where the temperature of the external side area of the cylinder is changed in the circumferential direction.

Решением задач деформации цилиндрических конструкций в температурных и силовых полях ученые всего мира занимаются более 100 лет. Рассматривались в основном одномерные и двумерные задачи (стержни, балки, пластины, тонкие оболочки, осесимметричные задачи теории упругости, бесконечно длинные цилиндры).

К середине прошлого века были построены разрешающие уравнения, описывающие деформацию оболочек вращения, а также получены точные решения простейших задач упругости и термоупругости, являющиеся в настоящее время классическими [1–13]. Абсолютное большинство точных решений реализовано в декартовой системе координат, так как уравнения в этой системе наиболее просты. Построено несколько решений осесимметричных краевых задач теории упругости в цилиндрических и сферических координатах [21–32]. Точных решений трехмерных краевых задач теории упругости практически не было. Решены были только уравнения относительно объемной деформации цилиндра и шара [9]. Это было связано с непреодолимыми на тот момент трудностями построения интегрируемых комбинаций разрешающих уравнений как относительно перемещений, так и напряжений.

С последней четверти XX века появилось большое количество приближенных решений, в том числе и трехмерных задач, основанных на численных методах. Численные решения позволили существенно увеличить число рассматриваемых областей, в том числе сложных конфигураций. Поскольку при численном решении не важно, в какой системе координат решать краевую задачу, использовалась декартова система координат.

Интерес к аналитическим решениям задач появился, когда встал вопрос о достоверности численных решений. Проверка могла быть осуществлена либо экспериментом, что затруднительно по финансовым и иным соображениям, либо сравнением с точными решениями.

Для увеличения числа аналитических решений краевых задач появилась необходимость получать решения в иных системах координат. Однако преодолеть трудности решения уравнений и выполнения краевых условий, близких к реальным, удалось не сразу.

Привести систему разрешающих уравнений трехмерной теории упругости в цилиндрической и сферической системах координат к отдельным уравнениям относительно каждой искомой функции и проинтегрировать их удалось авторам данной статьи [14–20]. Опубликованных работ по этому направлению нет. Настоящая работа обобщает эти ре-

зультаты на задачу теомоупругости.

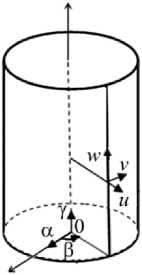
Рис.1. Цилиндрический резервуар

Fig.1. Cylindrical vessel

В цилиндрической системе координат а, р, у рассматривается несвязанная задача термоупругости для цилиндрического резервуара с жидкостью, причем первая координата отнесена к внешнему радиусу резервуара R, третья – к его высоте H, вторая координата – есть угол поворота вдоль направляющей. Таким образом, исследуемая область t < а < 1, - п < р < п, 0 < у < 1, причем r t = —, r - радиус внутренней боковой поверхности.

Система разрешающих уравнений задачи термоупругости может быть представлена следующим образом [8]:

AT = 0, Ае = 0,

A w +

R	1 де п д т	= 0,
( 1 - 2» )	8 ду 8 ду

Г 1 ) R Где   дT1 2 дv

I AIU +                П

( а2)   (1 -2и)_да    да_ а2 др

1 ) R Г1 де п дT

V +

а2) (1 - 2и)_адр а др

2 д u _п

+ —7— = 0 .

а2 др

Здесь u , v , w - перемещения вдоль координаты а, окружном р и вдоль у соответственно (рис. 1); е-объемная деформация; T - температура тела; а _т - температурный коэффициент линейного расширения; E , и- модуль упругости и коэффициент Пуассона; р-

плотность жидкости.

8 = H; п = 2(1 + и)ат, f =

R

2(1 + и)(1 -2и)р H

E

д ² £ д 1 д ² 1 д ² да ² а да а ² др ² 8 ² ду ²

Первое уравнение системы – есть уравнение теплопроводности для несвязанной задачи термоупругости, второе – уравнение относительно объемной деформации, включенное в систему разрешающих уравнений вместо соотношения

1 1 д (а и) 1 д V 1 д w е =----—- -■----■- —

R

а да а др 8 ду

используемого в дальнейшем в качестве дополнительного условия для определения значений «лишних» произвольных постоянных, появившихся в решении в результате повышения порядка системы после включения в нее уравнения А0 = 0 [14].

Точное решение системы (1) строится в предположении, что температура и перемещения линейны относительно координаты у. Этот вариант встречается при исследовании деформации резервуаров, заполненных жидкостью.

Периодическое по р решение системы (1) ищется в виде

T (а , р, у) = To (а , у) + Т (а, у) cos р, 0(а, р, у) = 0о (а, у)+ 01 (а, у) cos р,w(а, в, у) = Wo (а , у) + w (а, у) cosр,

и (а, р, у) = и0 (а , у) + и1 (а, у) cos р,    v(а, р, у) = v1 (а , у) sin р.

Замечание . Возможны другие варианты решения, когда меняются местами синусы и косинусы, а также комбинация этих решений.

После подстановки соотношений (4) в систему уравнений (1) приходим к двум системам уравнений

<52 1 д 1 д2 ) +         1

(да   а да а ду J

Т о = о,

< д ² 1 д 1 д ² ) + ^_ ~ । ~—~

(да   а да а ду J

0 о = 0 ,

< д ² 1 д 1 д ² )

++ W o

(да2 а да а2 ду (

R д

(1 -2и)а ду

(0о-П То),

и

д ²      1 д      1     1 д ² "

+               • ^и о

да2 а да а2 а2 ду

R д

( 1 - 2 и ) да

( ⁰ о ^-П ^То )

< д2 + £_д1_ + X д2 )T

(да2 а да а2 а2 ду2 J 1

< д ² 1 д 1 1 д ² V

+ 7---7+”—^ 01

(да2 ада а2 а2 ду (

< д ²     1 д      1     1   д ² )

++ W

(да2  ада  а2  а2 ду (

-

R д^    ,

п ..      .(01 П Т1),

(1 -2и)а ду

д ²      1 д      4     1 д ² '

( ^u 1 ^{+ v} 1 )

++

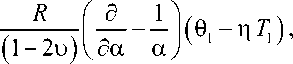
да2 а да а2 а2 ду2

д ²     1 д 1 д ²

^{( и}1 - ^v 1 ) = ^-

R < д 1

^^1 „ + ^_ ( 1 - 2 и ) (да а

1                             •

да2 а да а2 ду

Следует отметить, что последние два уравнения системы (6) получены как сумма и разность четвертого и пятого уравнений из (1).

С учетом предположения о линейности перемещений в направлении у считаем

Т (а , у) = Т„0 (а) + ТА (а) у, 0„ (а, у) = 0„,п(а) + 0„. (а) у, m,         m0m1, m,          m0m1,

wm (а , У) = wm0 (а) + wm 1 (а) У ,um (а , у)= um 0 (а) + um 1 (а)У,      vm (а , У) = vm 0 (а) + vm 1 (а)У, ( m = 0;1) •

После подстановки соотношений (7) в уравнения (5) и (6) получаем серию обыкновенных дифференциальных уравнений. В результате их интегрирования имеем

T oo ( a ) = B 0o + B 020 ln a ,      T a- ( a ) = B -- + B 02- ln a ,

0 00 ( ^a ) = ^{A -} 0 ⁺ А 0 ^{ln a} , 0 01 ( ^a ) = А^- - ⁺ А - ^{ln a} ,

R

-' ^|a|             .

C* + C 2 In a + - L-, a ² + L² —( In a - 1 )

00     00         401         014

И 0 ( “ ) = - (1 -₂u)_e ( C °- + C О- ln “ ) ’                            (8)

u 00

2 (1  2u) D00 a + D00 a + L00 a ln a u01

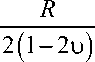
D 0_- a + D 0- — + L 21 a In a a

Если после интегрирования определить значения u ₁₀ , v ₁₀ и u ₁₁ , v ₁₁ , то

T 0 ( a ) = B ^ a + B ^l, T„ ( a ) = B -, a + B --- , a                 a

^О -0 ^{(a)   A} -0 ^{a + A} -0    ,

a

О -- ( a ) = A -^-- a + А 2 - , a

R I z~f2 ^{- -} r- _.3 ^- r2

^ -0 = -л      C -0 ^{a +} C -0   +o ^Ln^{a +}7T L -- ^{a ln a}

( -- 2 u ) e [ a 8        2

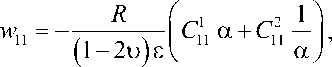
u ₁₀

v ₁₀

R

4 ( - - 2 u )

( ^{D -}0 ⁺ L -0 ) ^a 2 ⁺ D -0 A ⁺ L 20 ⁺ D -30 ⁺ D -40 ^{ln a x} ' a

u ₁₁

v ₁₁

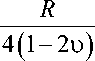
( ^D -^-0 ^- L -0 ) ^a 2 ^{+ D} -²0 ” ⁺ L ²0 ^- D -o ^{- D} -⁴0 ^{ln a x} ’ a

.„ R, X ( D - + L I- ) a ² + D^ + L ,²- + D ,³, + D ,⁴, ln a

4 ( - - 2 u ) L                   a

——— ( D -^-- - L -- ) ^{a 2} + D -²- —+ L ²- - D -³- - D -⁴- ln ^a

4 ( - - 2 u ) L                   a

Здесь ^A™ , B ^n , С ^п , D ^n ^- постоянные интегрирования,

kk k

^mn   mnnn   ¹1 mmn ^.

С учетом соотношений (4), (7) дополнительное условие (3) приводит к тождествам

1 f 1 d ( a u 00 )    1

R ^a d a

+ - W 01

£

)

, 0 0!

1 d ( a u ₀₁ )

R a d a

,

1 R

' 1 d ( a u ₁₀ )

_Va    d a

+ - ^v 10

a

. 1 )

+ - w_n

£ )

1 R

1 d ( a u_x J   1

" + - V 11 a d a    a

Подставляя в первые два из них соотношения (8), получаем

2(1 -2о)(А00 + А00 Ina) + 2D00 + L00 (2lna + 1) + — (Cm + C01 l"a) 0, 2(1 -2u)(A01 + А2 Ina) + 2D01 + L^ (2lna +1) - 0, откуда следует

2 ( 1 - 2u ) A. + 2 D 00 + L 0 +£ 2 C 01 = 0, ( 1 - 2u ) A . + L 00 + £ 2 C 1 = 0,

2 ( 1 - 2u ) 4 + 2 D 0, + L₆ 1 - 0, ( 1 - 2u ) А , + L 21 - 0.

А с учетом (10)

12    1     2 2 1             2     2 1 2

^{2 (}1  ^2u) А 00 ⁺ А 00 ^{+ 2} D 00   ^— B 00 ⁺ £ 2 C 01 ^- 0,  ^{2 (1  u) A} 00   ^— B 00 ⁺ £₂ C 01 ^- 0,

[2 ( 1 - 2u ) A 01 + А ' ] + 2 D 01 - n B 01 = 0,2 ( 1 - u ) 4 - — B 021 = 0.

В результате

2 ^01

£

⁽ 1 - ^{2 u )} А 0 + 2 А 20

— D ¹ -I-— R² D 00 ⁺ 2 B 00 ,

- 2 C 21 --2 ( 1 ^-u ) А 2 + ^— B 0 _O.

D 01 -- ( 1 - 2u ) A 11 +^ ) — B 01 , A ,21 -TT^ B 021 .

4 ( 1 -u )              2 ( 1 -u )

Из третьего условия (11) имеем

( In a +1 ) a

4 (1 - 2u) [ А110 a + А120 _ J+ 3 (D10 + L10) a - D120 ~ + (L2 0 + D130) _ +

V          a 7 ^{x 7} a ^x —' a

+ ( D ;„ - L 1 0 ) a + Ц 2Д + ( L 20 - D 1³0 ) - - D* "^a + 4 f C 111 a + C n -) - 0.

x ' a x —1 a a - V

Очевидно,

111  1     2242

^{4 ( 1  2 u) A}10 + ⁴ D 10 + ² L 10 + £ 2 C ^{11 -} 0, ^{4 ( 1  2 u)} А 10 ^{+ 2} L 1° + D 1° + £ 2 C ^{11 -} 0,

( 3 - 4 u ) A 1 ₀ + 2 D 1 ₀ -n Б \ _й +- 2 C 11 - 0,

^{( 3 - 4 u) A} 10 ^-— B 10 ⁺ 2 D 10 +- ? C 11 ^{- 0},

1 C 1 -— B 1 -1 3 -£ 2 ¹¹ 2 ¹⁰        2

A 10 - D 10 ,

-Lr2 -— R2

2 C 11 _n B 10 £        2

(3 - 4u)

A 10 - 4 D-

Последнее условие из (11) приводит к г 1 А                          Г 1        (lna +1)

4 (1 - 2u) I A, a + 4,2 - I + 3 (D^1 + L11) a - DX1—r + (L21 + D3) - + D,1

V          a) ^v ’ a ^x —’ a a

+ ( Dh- L 11 ) a + D 2A+( L 2, - D , ) - - D — ^ 0, ^x ' a ^x    —’ a a

2(1 - 2u) A, + 2D, + L,1 = 0 , (3 - 4u) A, + 2D, - n B\x=

2 (, - 2») 421 + L1 + , D 0,  (3 - 4u) 41 + 2 D, - П В,2

D¹ - Л/?^{1 (}3 ^4u) 4¹    D ⁴ - 2n Д² - 2(4 -4n1 A"

^D , 1 = 2 B ¹      2    ⁴ 1 , D ¹ = 2 ⁿ B ^{1 2 (} 3 4 ^{U) 4 1} .

Таким образом, получены соотношения, определяющие значения «лишних» постоянных интегрирования

_c

£

—c¹ £² C1¹

^{1 n} R^{2 D}00 ⁺ 2 B 00 ,

D 01 = - ( 1 - 2 u ) А 1 + 4         в 0²1 ,

= Л в 1 _13±

2 10        2

А 10   ^D 10 ,

1 C ’=- 2 ( 1 -u ) 4 00 +n В

— Г^{2 П} R²

C n     - ^B 10

£

00 ,

^П    R2

2 ( 1 -u ) ⁰¹ ,

⁽ 3  ^{4 u)} ^² -Ip⁴

2 10 4 10 ,

( 2)

D 1 =П В , -3--^)^ A 1 1 , D *1 = 2 n В ,', - 2 ( 3 - 4 u ) A , .

При исследовании деформации резервуара с жидкостью одним из обязательных граничных условий является условие, накладываемое на напряжение caa. Это напряжение определяется из соотношений Дюгамеля–Неймана и в принятых обозначениях имеет вид ст aa

E        Г 2 ( 1 - 2 u ) d и

+ 2 u0-p T >.

2 ( i +u )( i -2u ) [    R da

Соотношения (4), (7), позволяют считать

^CT aa (^a , P , Y ) = ^CT aa 00 (^a) ^{+ CT} aa 01 (^a) Y ⁺ [ ^CT aa 10 (^a) ^{+ CT} aa 11 (^a) Y] cos P -

Тогда

E Г 2 ( 1 - 2 u ) du_{mn n}

+n T m„ ^ , ( m ; ⁿ = 0;1 ) -

CT aamn

---- ------ J-- X------ L--mn - 2 u0 2 ( 1 + u )( 1 - 2 u ) [      R d a

После подстановки входящих в эти уравнения соотношений с учетом (12) получаем

^CT aa 00

E

2 ( 1 + u )( 1 - 2 u )

-

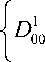
— ^{- 2 u} А 00 + a

⁺ [ 1 ^{+ ( 1 - 2 u) ln a]} А 00 ^{+ n} ( ^B 00 ^{- B} 020 ) } .

^ аа 01

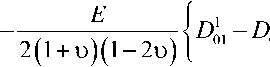
— - 2 о А 01 + а

+ [ 1 + ( 1 - 2 о ) In а] < + п ( В 11 - В 1 ) } ,

° аа 10

E

2 ( 1 + и )( 1 - 2 и )

D>- D

-1Т + D а

— +

2 а

+ ( ^{1 - 2 и} ) А 110 ^{а -} 2 U А О + ^п В 120 2 , а а I

° аа 11

-

E

dm а - D121 — + D14 — + а     2а

+ (1 - 2и) А> - 2иА11 - + п В121 - 2 . а а I

Решаем краевую задачу: цилиндрический резервуар с жидкостью находится в несимметричном температурном поле.

Для температурной задачи принимаем следующие краевые условия. Оба торца резервуара и его внутренняя боковая поверхность термоизолированы от внешней среды, то есть дT(а , в, у)

да

а= t

= 0,

д T ( а , в , у )

ду

Y= 0

= 0,

д T ( а , в , Y )

= 0.

Внешняя боковая поверхность имеет температуру

T (1, в, y) = @00 +010 cos в , параметры 000,010 постоянны. С учетом соотношений (4), (7), (8), (9) имеем

T ( ^а , ^в , y ) = T 00 ( ^а ) + T 01 ( ^а ) Y ⁺ [ T 10 ( ^а ) ⁺ T 1 (^аИ ] ^{cos в} =

B 00 ^{+ B} 00 ^{ln а +} ( B 01 ^{+ B} 01 ^{ln а} ) ^{Y +}

B 110 а + B 1 ² ₀ - + | B 111 а + B 121 - IY а I            а J

cos в ,

^д T ^(а , ^в , Y)_ „2 1    _R2 1

= B00   + B01   Y + да        а а

B 110 ^- B 10 ~ ⁺ [ ^B 11 ^{- B}u “I^Y а ' а ;

cos в ,

дT(а , в, Y)     1      2 , Г 12 cos в.

—= в1 + в2 in a + в1 а + B2 -01      01               1111

дY[а

Из первого граничного условия

^B 00 ^{+ в} 01 Y ⁺ [ B 110 ^{+ B} 1 ² 0 ⁺ ( B 111 ⁺ B 121 ) y] ^{cos в} = ⁰ 00 ^{+ 0} 10 ^{cos в} ,

^B 00 = ⁰ 00 , ^B 01 = ⁰ , ^B 10 ^{+ B} 10 = ⁰ 10 , ^B 11 ^{+ B} 11 = ⁰ .

Из второго

2 1      7 1

B ₀ ² ₀ t + B . t Y +

^B 10   ^B 10 t ₂ ⁺^ ^B 11   ^B 11 t 2 |^Y

cos в = 0,

откуда следует

^B 00    ⁰ ,    ^B 01    ⁰,   ^B 10   ^B 10 1 2    ⁰,   ^B 11   ^B 11

-1 = 0. t ²

Тогда

B 0 - B ^0

1 t ²

10 /2 Л ^10 ,

2 = 0,   B10 + B10 = ®10 , ^ B10 ~ ( 2 , \ ®10 , t                                              (12 + 1)

12     12 1       1  2

^B 11 + ^B 11    ⁰,    ^B 11   ^B 11 1 2 ⁰, ^ ^B 11    ^B 11    ^0.

В итоге

B 0 =© oo , B^ = 0, B o2o = 0, B^ = 0, Bh = B 2 = 0,

2 t 1 1

10 /2         10 , 10                 10 ,

( t ² + 1 )                 ( t ² + 1 )

то есть в рассматриваемой краевой задаче B ₀ ¹ ₀ , B ₁ ¹ ₀ , B ₁ ² ₀ не равны нулю, остальные – нули.

8T(a , в , y)

При полученных значениях постоянных интегрирования ---------- = 0, следова-

5у тельно, все краевые условия температурной задачи выполняются.

Граничные условия упругой задачи принимаем в следующем виде:

aaa( t, в , y) = Pн (1 -y) , w (1, в ,0) = 0, w (1, в ,1) = 0, w (t, в ,0) = 0, w (t, в ,1) = 0, u (1, в ,0 ) = 0, u (1, в ,1) = 0, v(1, в,0) = 0, v(1, в,1) = 0, v(t, в,1) = 0 v(t, в ,0) = 0.

Кроме этих условий имеем соотношения

£

— Г¹ = ^П R¹

2 ^L 11 _n B 10 £        2

D ¹

00 ,

D 11 =- ( 1 - 2 u ) А 01 -

^u ) __D1

2     А 10 D 10 ,

£

£ 2 C 2, =- 2 ( 1 -u ) А 2, ,

А 0 1 = 0,

= ^ B0

( 3 ^{4 u)} X² -1D*

2 10 4 10 ,

( 3^4 2 1 а

2 11 ,

которые с учетом (14) следуют из (12).

Из (4), (7) и (13) имеем

w(a , в , y) = w00 (a)+ w01 (a) Y + [w10 (a)+ w11 (a) y] cos в, u00 (a) + u01 (a) Y + [u10 (a} + u11 (a) y] cos в, v(a , 3 , Y) = [v10 (a)+ vn (a) y] sin3,

^ аа (^а , Р , Y ) = 4,. 00 (^а) + 4,. 01 (^а) Y + [^ аа 10 (^а) + ^ аа 11 (^а) Y] cos Р •

В результате из условий (15) получаем

W00 (1) + W10 (1) cos Р = 0 , wоо (1) + woi (1) + [wio (1) + wn (1)] cos P = 0, woo ( t ) + W10 ( t ) cos P = 0 , w00 ( t ) + W01 ( t ) + [ W10 ( t ) + W11 ( t )] cos P = 0,

u00 (1) + uio (1) cos P , u00 (1) + u01 (1) + [uio (1) + uii (1)] cosP = 0 , 4o(1) = 0, 4o(1) + 41 (1) = 0, 4o(t) = 0, 4o(t) + 41 (t) = 0,

4„ (t , P , Y) = 4„00 (t ) + 4,.01 (t ) Y + [^аа10 (t ) + ^аа11 ( t) Y] cos P = PН (1 - Y) , откуда следует woo (1) = 0, W10 (1) = 0, W01 (1) = 0, W11 (1) = 0, woo ( t ) = 0, W10 ( t ) = 0, W01 ( t ) = 0, W11 ( t ) = 0, uoo (1) = 0, U10 (1) = 0, u 01 (1) = 0, U11 (1) = 0,                        (17)

4o ( 1 ) = ⁰, 41 ( 1 ) = ⁰, 4o ( t ) = ⁰, 41 ( t ) = ⁰,

^ аа» ( t ) = P Н , ® „а 01 ( t ) =^-P ^Н , ° «,. 10 ( t ) = ⁰, ® аа 11 ( t ) = ⁰.

Из w ₀₁ ( 1 ) = 0 и w ₀₁ ( t ) = 0 с учетом соотношений (8) имеем систему C 11 = 0, C 11 + C 21 ln t = 0, откуда C 11 = C 21 = 0. Теперь из второго соотношения (16) получаем 4 00 = 0, из первого D 00 =- ( 1 - 2 и ) А 0 ₀. Из третьего и четвертого имеем

D 01 =- ( 1 — 2 u ) 4 11 ,

4 21 = 0.

^Из     w oo ( 1 ) = ⁰

^C 10 ^{+ C} 0 ² 0 ^ln t ⁺ 4 ^{4 1} 1 t ²

и    w ₀₀ ( t ) = 0 с учетом (8) получаем    C 0 ₀ + 4 А 11 = 0,

= 0, откуда следует

C Oo =- 4 4 01 , C 2 =

(t2-1)

4ln t

А 0¹1

Из W 11 ( 1 ) = 0 и W 11 ( t ) = 0 с учетом (9) имеем систему

C11 + C121 = 0, C111 + C^ = о, откуда следует

C 11 = C 121 = 0.

После чего из оставшихся соотношений (16) имеем

1 ^П R1 ⁽3 4ц) 1        4          2                 z<2

D 1o = 2 B 1o       2     ⁴ 1o ,   D 1o = 2 ⁿ B 1o   ^{2 ( 3  4 u) 4} 1o ,

D1, =-(3-24U) А,1,, D‘=-2 (3 - 4u) А2.

Из w ₁₀ (1) = 0 и w ₁₀ ( t ) = 0 с учетом (9) приходим к системе уравнений

12 1 1      122 1 14 1 22

C10 + C10 + о A11 0,   C10 t + C10 + о A11 t + n A11 t ln t 0’ откуда следует

t ² ln t ₂

=-11

- 8 ^А“ ( t 2 ^{+ 1} ) ’ C² =

t ²ln t

² t

² 2 t 1

A n ⁺ 8 A n

Из и ₀₀ ( 1 ) = 0 и и ₀₁ ( 1 ) = 0 с учетом (16) приходим к системе

< + D00 = 0, D01 + D = 0, откуда следует

21 21

00    ^00 ’ ^01    ^01 ’

D 00 =- D > = ( 1 - 2 и ) А 00 ,   D 01 =- D 01 = ( 1 - 2 и ) А_г

^И з ^ аа 00 ( t ) = Р ^Н и ° аа 01 ( t ) = -Р ^Н имеем

D 00 ^{- D} 00 t ^{- 2 и} А 00 ⁺ⁿ B 00 = ^- f , D 01 ^- D ² t ^{- 2 и} А 01 = f ,

1 (t2+1)          1         1                   1 (t2+1)

D »   t    -²» А 00 +П B 00 =- f , D      -2u А 01 = f ,

, (t2+1)                                                          (t2+1)

-(1 - 2v) А00---22oА00 +n B00 =- f ,  -(1 - 2u) А01---22u А01

1 t ² ( f ^{+ n B} 00 ⁾       1 t ² f

А”    ( t ² + 1 - 2 u ) ’   А 0 ¹      ( t ² + 1 - 2 u ) .

Из u ₁₀ ( 1 ) = 0, v ₁₀ ( 1 ) = 0 , v ₁₀ ( t ) = 0 с учетом (9) следует

11  1 2223

D 10 ^{+ А} 10 П " 10 ⁺ D 10 ^{+ А} 10 П " 10 ⁺ D 10 = 0,

11  1 2223

D 10 ^А 10 ^+п " 10 ⁺ D 10 ^{+ А} 10 ^п " 10 D 10 = ⁰’

11  142  2  23242

( D 10 ^{- А} 10 ^+п " 10 ) t ⁺ D 10 ⁺ ( A 10 ^-n B 10 ^- D 10 ) t ^{- D} 10 t ^ln t = 0.

Суммируем первые два уравнения и вычитаем из первого уравнения второе:

D 10 ⁺ D 10 ⁺ A 10   ⁿ B 10 = ⁰’ A 10   ⁿ B 10 ⁺ D 10 = ⁰

12   2   2    311

D10 + D10 = A10 +n B10 ’    D10 =n B10

Ранее было установлено, что

П¹    — R^{1    (2}  4ц) ,        4 _      2 - /,. _ Д \ ^2

D10 = 2 B10      2    А*0 ’   D*0 = 2П B*0 + 2 (3  4U)

следовательно,

Л¹ । Г)² — — Л ² । n R²     Л² — — ^П R1 । ⁽³ 4ц) 1 _ 2       д2

D io + D io = A io ⁺ Л B io ,   D io = 2 B ^{w +} 2    Аю   a 'o ^{+ П} b '⁰ ,

_П2 ЛЬ 02 __Ri \ , (3-4^и) 1

D io = 2 ( ²B io B io ) ⁺    2 А ю

-4, D ^ =n B io - A io .

или

_i 2        ( t ² -I )

Таким образом, C ^o = - 4 A 1i , C Jo = ——---

t ² ln t 2 1 122 t ² ln t 2 t ²112

2 ( ₁ 2 -1 ) A i 8 A ii ⁽ t ^{+ 1 )} ’ C io = 2 ( _t 2 -1 ) A ii ⁺ 8 A ii , C ii    C ii   ^o ,

n i — ⁿ Ri

D io 2 B io

⁽ 3 4 ^u) A¹ D²

2 10 , 10

Д M «2 _ Ri   I ^{( 3 4 U)} Ji _ j2

2 ^{( 2} B io   B io ⁾⁺ 2     ^A io   A io ,

D 3o =n B io - A io , D io = 2 n B i ² o - 2 ( 3 - 4 » ) A io ,

D ii "'J'') A ', .      D 4 =- 2 ( 3 - 4 v) A 2 .

Из третьего уравнения системы ( 8) с учетом ( 9) получаем

■ B 1

2 0

- ^{(3 4 u} ) _Л1 _J1 _{+ S}1

2 io ^io ⁺ 'I ^uio

. 4 , ^ПМ R2 R ^{3 4 U)} Д 1 4² + t ⁺ ~ ( ² B i o ^- B i o ) ⁺ 2 ^A 1 o ^{- A} 1 o ⁺

+ ( A ² -n B i ² o -n B 1о + A i 'o ) t ² -[ 2 n B i ² o - 2 ( 3 - 4 u ) A 2 ] t ² In t = o ,

[ ( 3 - 4 u ) ( t ² + i ) + 2 1 ² ] ( t ² - 1 ) A '_o - 2 [ t ² - 1 + 2 ( 3 - 4 u ) t ² In t ] A ² _o -- n [ 3 t ⁴ - 2 1 ² - i ] B 1 _o + 2 n [ 2 1 ² In t + 1 ² - i ] B 1 ² _o = o ,

то есть одно из уравнений для определения оставшихся постоянных интегрирования А ₁ ¹ ₀ , A ₁ ² ₀ .

Выполним условие o_{aa io} ( t ) = o . Подставляя в

^ ааЮ

E J_ 4 ( 1 - 2 u ) du _io 4 ( 1 + u )( 1 - 2 o ) [ R    d a

- 4 u0 ,o + 2 n T ,o ^,

используя соотношения (9), получаем

^ aa io ( t ) = -

E

4 ( 1 + u )( 1 - 2 u )

1 - 4vl A io t + A ² 1 1 + 2 nl B io t + B i ² o 1

^ = o,

14    2   42          14     22      22

2 D io t — 2 D io + D io t + 2 ( 1 — 2 u ) A ,o t — 4 u A ,o t + 2 n B io t — o,

2 D 1_o t ⁴ - 2 d ,²_o + D 4 t ² + 2 ( 1 - 2 u ) A '_o t ⁴ - 4 u A ² _o t ² + 2 n В^ t ² = o.

С учетом (19) приходим к уравнениям

2 D 10 1 ⁴ - 2 D. 0 + D 0 1 ² + 2 ( 1 - 2 u ) А } ₀1 ⁴ - 4 u 4, 0 1 ² + 2 n B q 1 = 0,

[ⁿ B 10 ^{- ( 3 - 4 u)} А 10 ] ^{1 4 - n} ( ² B io ^- B 10 ) ^{- ( 3 - 4 u)} А 10 ^{+ 2} A 1O ⁺

+ [2n B20 - 2 (3 - 4u) 420 ] 12 + 2(1 - 2v) 4^014 - 4u A2012 + 2n В2012 = 0, [-(3 - 4u-2 + 4u) 14-(3 - 4u)] А10 + [2 + (-6 + 8u-4u) 12 ] 420 +

+ n( 14 +1)B^ +n(412 -2)B;« = 0,

( 1 ⁴ + 3 - 4 u ) А 1 ₀ + 2 [ ( 3 - 2 u ) 1 ² - 1 ] 4 2, - n ( 1 ⁴ + 1 ) B'_to - 2 n ( 2 1 2 - 1 ) B o = 0.

Итак, имеем пару уравнений относительно А ₁ ¹ ₀ , А ₁ ² ₀ :

А 10 [ ( 3 - 4 u ) ( 1 ² + 1 ) + 2 1 ² ] ( 1 ² - 1 ) + 2 A ² ₀ [- 1 ² + 1 - 2 ( 3 - 4 u ) 1 ² In 1 ] -- n B w ( 3 1 ² + 1) ( 1 ² - 1 ) + 2 n B 2 ( 2 1 ² ln 1 + 1 ² - 1 ) = 0 ,

(14 + 3 - 4u) I + 2 [(3 - 2u) 12 -1] А2 - n ( 14 +1) C - 2n (212 -1) B2 = 0 .

Выполним оставшиеся граничные условия из (15) u₁₁ ( 1 ) = 0, v _n ( 1 ) = 0, v _n ( 1 ) = 0,

. .                                                           1       (3 - 4и) 1             4/ А оаа11 (1 ) = 0, добавив к ним соотношения D^ =--—2—~41,    Di =-2(3-4и)4л из

(16). Из (14) имеем B ₁ ¹ ₁ = B 2 = 0, откуда следует L₁₁ = A ^ , L 2 ₁ = A ₁ ² ₁ . Из указанных граничных условий имеем систему шести однородных уравнений

11 223   11223

^D11 ^{+ A}11 ⁺ D 11 ^{+ A}11 ⁺ D 11 = 0,      D 11 ^{- A}11 ⁺ D 11 ^{+ A} 11 ^- D 11 = 0,

11221  2  34

( ^D 11 ^- A 11 ) ^{1 +} D 11 1 2"⁺ A n ^{- D} 11 ^{- D} 11 ^{ln 1} = ⁰,

D11 - D2 -1 + D4 — + (1 - 2и) А11 - 2иА2 1 = 0 , 11        11 t3 11 2t 1111

D\1 +(3-24U) А11 = 0,     D141 + 2 (3 - 4и) А2 = 0, решение которой единственное, следовательно, нулевое:

A 11 = A² = D 11 = D² = D 3 = D⁴ = 0.

Таким образом, постоянные интегрирования А ₁ ¹ ₀ , А ₁ ² ₀ определяются из системы (20), значения остальных постоянных интегрирования имеют вид

1  21212

B 00 = ^ 00 , B 00 = 0, B 01 = B 01 = 0, B 11 = B 11 = ⁰ ,

2 t 1 1

10 /2     ^10 , 10 /2     ^10 ,

(12 + 1)                 (12 + 1)

12 (f+nB)

А 00 = ,' , /"? , 4 2, = 0, А 11 =- тАг-ГЛ , А 21 = 0, A 1 = A 1 = 0, ( 1 ² + 1 - 2 u )                     ( 1 ² +1 - 2u )

С ¹ = Л а° С² -⁽) Л¹ С¹ = С2 =0

00       0         00                ^1 , ^01 *^01 ^v,

4             4ln t

C0 = C,20 = 0, <} = <1 0,(21)

D 00 =- ( 1 - 2 » ) -4.- D 00 = ( 1 -29 4 ,- D 0, = - ( 1 - 2 » ) AD 0, = ( 1 - 2 u ) А„

£)¹ -Л #' -(3 4°) A¹ D² -ⁿf2 В² -В¹ 1 __ 4^u) A¹ -A²

D10   2 B10      2    А10’ D10   2 (2 B10  B10) +    2    А10

D 30 =П B 10 - A, D m = 2 П B 120 - 2 ( 3 - 4 u ) 4, D = D ^ = 0.

Теперь

T(а , в , y) = B0o + | Bio а + B120 - |cosв , Vа 7

0(а, в, y) = А0о + А01 y + I А1о а + А, - I cos в, Vа 7

w (а, в, y) = -

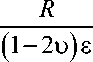
C 1_n + C ^: _n In а + ¹ А а 00      00                01

u ( а , в , y ) = -

R I ^1       ^2 1 i ^1       ^2 1 i

7 ] D00 а + D00 + I D01 а + D01   I Y +- 2u) I а V а 7

+ —

( ^D 110 ⁺ L 10 ) ^а 2 ^{+ D} 120 ~ ⁺ L ² 0 ^{+ D} 130 ^{+ D} 10 ^{ln а}

cos в r ,

D110 - L10 ) а2 + D10 — + L20 - D10 - D140 ln а ' а sin в,

E

а,., =--------------[v9 - (1 + и)аг T ].yy (1 + u)(1 - 2u)[               T ]

Вычисления проводились для следующих параметров задачи:

R = 10м, r = 9,95м, H = 30м, E = 7,0-104 МПа, u = 0,34, p = 0,75 • 103 ---, аТ = 23• 10-6-----, 000 = 60°С, 010 = 25°С.

м3 град

Оказалось, что перемещения v , w пренебрежимо малы, как и смещение u точек наружной боковой поверхности. Перемещения u точек внутренней боковой поверхности практически не меняются по высоте и не превышают 0,004 толщины стенки резервуара.

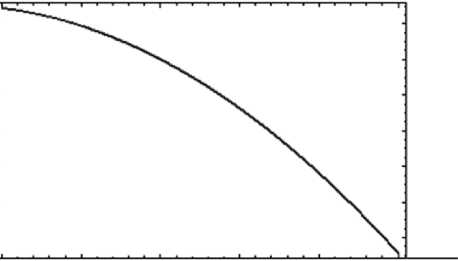
Максимальным при указанных параметрах задачи является напряжение oyy , и меня ется оно только по окружной координате, практически не завися от а и y . На рис. 2

представлено распределение напряжения

ап(а ,0,0,5) E

по а от внутренней до внешней

боковых поверхностей резервуара.

-0,00296897

-0,00296897

-0,002296897

-0,002296898

-0,002296898

-0,002296898

-0,002296898

0,995   0,996   0,997   0,998    0,999    1,000 «

Рис. 2. Распределение напряжений по координате

• Fig. 2. The stress distribution on coordinate

На рис. 3 показано распределение того же напряжения по окружной координате от в = 0 до в = п .

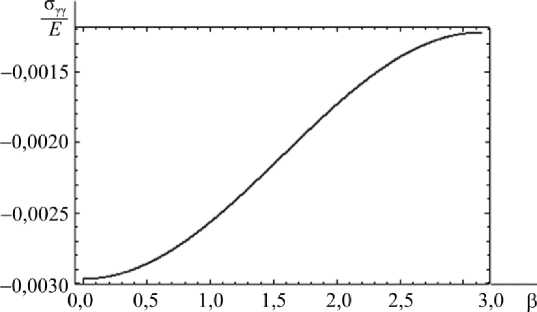
Рис. 3. Распределение напряжений по координате

Fig. 3. The stress distribution on coordinate

Остальные напряжения значительно меньше.

Без учета влияния температуры качественная картина та же, но максимальные напряжения на 1–2 порядка меньше.

Итак, точное решение поставленной краевой задачи построено.