Краевые задачи для неоднородных систем полигармонических уравнений с приложениями в теории тонких оболочек и пластин
Автор: Микишанина Е.А.
Статья в выпуске: 4, 2019 года.
Бесплатный доступ
Ряд задач теории упругости, теории гетерогенных сред, теории тонких оболочек и пластин сводится к решению краевых задач для систем неоднородных полигармонических уравнений. В работе предложен численный алгоритм решения систем полигармонических уравнений вида в односвязных областях с кусочно-гладким контуром с заданными граничными условиями. Рассмотрены два случая, когда функция является известной полигармонической функцией и когда функция является также искомой полигармонической функцией. Граничные условия могут иметь вид, аналогичный условиям Дирихле, условиям Неймана, а могут иметь смешанный вид, когда на одной части границы заданы условия типа Дирихле, а на другой - условия типа Неймана. На основе многократного применения оператора Лапласа и метода граничных элементов, в основе которого лежит интегральное тождество Грина, заданная система сведена к системе интегральных тождеств. После аппроксимации границы вписанным N -угольником и дискретизации системы интегральных тожеств последняя сведена к системе линейных алгебраических уравнений, которую удобно представить в виде системы матричных уравнений. Существование и единственность решения следует из существования единственного решения системы линейных алгебраических уравнений. Особое внимание уделено приложению построенного алгоритма к решению задач об изгибе тонких пластин, причем изгибающая нагрузка может быть известной функцией, а может быть неизвестной полигармонической функцией произвольного порядка с заданными граничными условиями. Решена задача об изгибе тонкой пластинки эллиптической формы с известной нагрузкой на поверхности, а также задача об изгибе тонкой квадратной пластинки с неизвестной нагрузкой, являющейся решением гармонического уравнения с заданными граничными условиями. Построены линии уровня и приведены формы изогнутых пластинок.
Система, полигармоническое уравнение, краевая задача, граничные условия, дискретизация, тождество грина, численный алгоритм, тонкая пластина, изгиб, изгибающая нагрузка
Короткий адрес: https://sciup.org/146281959
IDR: 146281959 | УДК: 519.635 | DOI: 10.15593/perm.mech/2019.4.13
Текст научной статьи Краевые задачи для неоднородных систем полигармонических уравнений с приложениями в теории тонких оболочек и пластин
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2019PNRPU MECHANICS BULLETIN
Исследование проблем механики, теории оболочек и пластин, теории гетерогенных сред предполагает решение краевых задач для систем дифференциальных уравнений в частных производных. В пространственном случае зачастую возникает сложность в постановке граничных условий, поэтому ограничимся рассмотрением плоских задач.
Ряд задач механики сплошной среды сводится непосредственно к системам эллиптического типа (системам полигармонических уравнений), например задача об изгибе тонкой пластины. В плоской теории упругости исследование изгиба пластин связано с решением дифференциального уравнения Софи Жермен для функции прогиба
A 2 u = q- , (1)
D где D - цилиндрическая жесткость пластинки в области T, которая задает форму пластинки. Если нагрузка q(x, у) является полигармонической порядка m (она может быть как заданной, так и неизвестной), то реше- ние задачи сведется к решению системы полигармони-ческих уравнений л 2, q
а и =
D
A mq = 0.
Граничные условия будут задаваться в зависимости от способа закрепления кромки и вида функции нагрузки на границе.
Задачи определения напряженного состояния водонасыщенной упругопористой среды [13], определения контуров обводнения области от источника [14] также сводятся к системе полигармонических уравнений.
Исследование изгиба достаточно пологих упругих оболочек предполагает решение системы
А2ф- Eh Aw = 0,
, 1 л 1
A w +-- Аф = —q ,
DD
где E - модуль Юнга; D - цилиндрическая жесткость; h - толщина пластины; ф(x, у) - функция напряжений; w(x, у) - нормальное перемещение точек срединной плоскости; q(x, y) – распределенная нагрузка, действующая по нормали.
Подробное решение дифференциальных уравнений эллиптического типа представлено в монографии И.Н. Векуа [3] и трудах современных авторов [5, 9, 11, 12, 22, 23, 29]. Например, монография F. Gazzola, H.-Ch. Grunau, G. Sweers [23], как и монография Векуа, охватывает линейные и нелинейные эллиптические краевые задачи более высокого порядка в ограниченных областях. В этой работе формулируются краевые задачи для систем полигармонических уравнений и анализируется существование и единственность их решений в функциональном пространстве. Во всех перечисленных работах приведены аналитические решения поставленных краевых задач в некоторых, достаточно простых, областях. В работах [11–12] решались различные системы дифференциальных уравнений, в том числе и эллиптического типа, в классе почти-периодических функций с помощью обобщенного дискретного преобразования Фурье. В этих работах задачи решались в областях, представляющих собой одно-, многослойные полосы и полуплоскости. Использование этих методов, например, в многосвязных областях с произвольной границей довольно затруднительно. Применение аналитических методов вообще возможно лишь в областях специального вида.
Поэтому имеет смысл применить прямые численные методы, которые бы позволили рассчитать искомую функцию в односвязной или многосвязной (в зависимости от условия задачи) области произвольной формы с непрерывной кусочно-гладкой и несамо-пересекающейся границей d T .
В настоящее время для численного решения краевых задач для полигармонических уравнений чаще используют метод конечных элементов [30], который требует использования всех точек области, что при вычислении, например, производных от искомых функций приводит к существенным погрешностям. При решении системы полигармонических уравнений этот метод довольно трудоемок, как и метод виртуальных элементов [28], предложенный авторами [20] для решения именно полигармонических уравнений, так как требует четкого разбиения области на элементы определенной формы. В последние годы для решения узкого спектра задач также используется метод Монте-Карло [24], в основе которого так же, как в конечно-разностных схемах, лежит метод сеток, который снова требует использования внутренних точек области. При использовании этого метода требуется решение дополнительной трудоемкой задачи: составить систему уравнений, отражающих взаимосвязи между погрешностями и значениями, что, в свою очередь, усложняет процесс решения исходной задачи. Поэтому с точки зрения простоты и эффективности метод граничных элементов выигрывает.
В работе [5] методом прямого численного разложения полигармонического уравнения краевая задача была сведена к системе линейных уравнений, в результате был разработан простой численный алгоритм вычислений полигармонических функций. В основе этого алгоритма лежит метод линейных граничных элементов [1, 2], который является одним из эффективных методов для решения указанного класса задач. Серия численных результатов подтверждает эффективность и высокую точность вычислений.
Ниже дается обобщение численных методов [7, 17] на системы линейных дифференциальных уравнений специального вида (аналог задачи Пуассона с известной правой частью или системы полигармонических уравнений):
A n u ( x, у ) = v ( x, у ), A m v ( x , у) = 0.
Граничные условия определяются особенностями моделируемого сценария.
В данной работе построен четкий алгоритм решения системы полигармонических уравнений специального вида (4). Ранее уже делалась попытка сформулировать краевые задачи для полигармонических систем [27]. Однако четкий алгоритм сформулирован не был. Автор попытался восполнить данный пробел, сформулировать строгий алгоритм для решения системы (4) и продемонстрировать этот алгоритм при решении задачи об изгибе тонкой пластины эллиптической и прямоугольной формы.
Система уравнений (4) является упрощенной, но численный алгоритм может быть применим для системы линейных уравнений произвольного порядка.
Рассматриваются два случая: 1) u ( x , y ) является искомой полигармонической функцией порядка n , непрерывной вместе со своими производными до ( n - 1) -го порядка включительно, v ( x , y ) является заданной полигармонической функцией порядка m также непрерывной вместе со своими производными до ( m - 1) -го порядка включительно в области T = T ^дT ; 2) u ( x, у ) является искомой полигармонической функцией порядка n , непрерывной вместе со своими производными до ( n - 1) -го порядка включительно, v ( x, у ) также является искомой полигармонической функцией порядка m , непрерывной вместо со своими производными до ( m - 1) -го порядка включительно в области T = T ^дT . Ссылаясь на результаты Векуа, мы оставляем в стороне теоремы существования и единственности решения и основное внимание обращаем на построение численного алгоритма и его применение при решении некоторых задач теории тонких оболочек и пластин.
1. Аппроксимация границы области и интеграла по границе
Ограничимся рассмотрением односвязной области произвольной формы с непрерывной кусочно-гладкой и несамопересекающейся границей дT. Данный алго- ритм можно обобщить на случай многосвязной области. Границу аппроксимируют вписанным многоугольником с N сторонами (элементами), угловые точки называют узлами (рис. 1). Количество узлов равно N . Если на границе есть угловые точки, то они совмещаются с узлами. Граничные условия удовлетворяются в средних (контрольных) точках элементов.
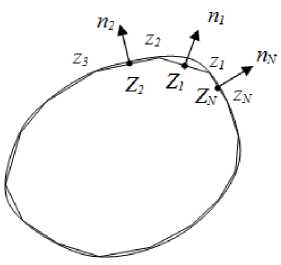
Рис. 1. Аппроксимация области вписанным многоугольником
Fig.1. Approximation of a region by an inscribed polygon
Компонентами матрицы M являются интегралы по элементам h m : M m = f g ( Zk , s ) ds . hm
Воспользовавшись интегральными представлениями [17], полигармоническое уравнение A n u = 0 с учетом представления (6) можно представить в виде системы линейных интегральных уравнений [8]:
n — j —1
S uj + £ f uj + p H p ds —
P=0 8 T n—j—1 _________
— E f qj+pGpds = 0, (j = 0, n — 1),(8)
P =0 8 T где
, du, _ , x x dGp_ u =Aju, Qj = —, APG (r) = G(r), Hp = —, (9) dnd r – расстояние от фиксированной точки z до переменной точки z' на гладкой границе. Поскольку в контрольной точке Zk контур гладкий, то множитель S = 1/2; во внутренней точке s = 1. Третье уравнение в (9) есть
Пронумеруем узловые и контрольные точки zj = ( x , y j ) ( j = 1, N ) , причем zN + 1 = Z1 , и Z k = ( X k , Yk ) ( k = 1, N ) , тогда геометрические характеристики границы в контрольных точках, таких как контрольная точка, длина элементов, координаты дуговой абсциссы и внешняя нормаль к контуру d T , определяются в виде
обыкновенное дифференциальное уравнение вида
( 1 d dG j ( r ) Y r ^^- I
( r dr dr J
ция [10]:
= G (r).
Решением
является функ-
G =
1 r 2 j
2 n 4 j ( j !) 2
1j ln;+E r m=1
m
7 = z k +1 + z k k 2
hk = |zk+1 — zk I,
2. Дискретизация уравнений (8)
nk =
k
S k = E h m =1
h k
2,
( y k +1 - y k
I h k
—
x k +1 — x k hk
Пользуясь приближенным представлением (6) или (7), можно записать уравнение (8) в виде линейной системы дискретных значений функции u j ( Zk ) и нормальной производной q j ( Zk ) = n k A u j ( Zk ) в контрольных точках:
Рассмотрим две функции u (z) и g (z, z'), z, z 'edT -первая функция непрерывна на границе, в то время как функция g(z, z ‘) может иметь в точке zk интегрируе- мую особенность. Интеграл от произведения функций по контуру определяется по формуле о нем, допускающей ошибку порядка О(max(hm)): m двух сред-
| n — j —1 N ^
1 u , ( Z k ) + EE uy + p
2 P =0 m =1 ^
( Z m ) f H p ( Z k , z ‘ ) ds ( z ' ) —
)
— Qj+P ( Zm )f GP (Zk , z ‘) dS ( z') = 0 hm J или в виде n матричных уравнений
J (Zk) = f u (z') g (Zk,z')ds (z') ~
5 T
N
*S U (Zm ) f g (Zk , z') ds (z')• m =1
m
Приближенное значение интеграла может быть записано в виде произведения матриц
J = MU .
n — j —1 _________
-и ^ + Е ( H p U j + p — G p Q j + p ) = 0, ( j = 0, n — 1 ) • (10)
-
2 p =0
-
3. Краевые задачи
Равенство (10) представляет n уравнений относительно N компонент Uj,k и Qj,k, (k = 1, N), которые являются элементами матриц U j и Q j и определяются как Ujk = uj (Zk), Qjk = qj (Zk), элементы матриц Hp и G p определяются как значения интегралов
Hp, km = J Hp (Zk, z9 ds (z ‘) и Gp, km = J Gp (Zk, ^9 ds (z9 hm hm соответственно.
1-й тип. Пусть функция v ( z ) непрерывно дифференцируема m раз в замкнутой области T и является известной полигармонической функцией порядка m . Тогда второе уравнение системы (4) удовлетворяется тождественно. Применяя m раз оператор Лапласа, получаем одно полигармоническое уравнение порядка m + n :
Am+nu = 0.(11)
В соответствии с формулой (10) уравнение (11) записывается в виде системы матричных уравнений
1 n + m - J -1
1U.+ У (Н и. -G Q ) = 0, 9 j Z—i\ p j+p p^+j+p) ’ 2
(J = 0, n + m -1).
Компонентами матриц и векторов являются значения соответствующих функций в N контрольных точках, найденных, как указано в предыдущем пункте.
2-й тип . Функция u ( z ) является искомой полигар-монической функцией порядка n , непрерывной вместе со своими производными до ( n - 1) -го порядка включительно, v ( z ) также является искомой полигармониче-ской функцией порядка m , непрерывной вместо со своими производными до ( m - 1) -го порядка включительно в области T = T ид T . Она определяется из второго уравнения системы (4) с m граничными условиями. Если представить это уравнение в виде системы (12), то для его решения необходимо задать дополнительно mN значений в контрольных точках.
Применив к первому уравнению системы оператор Лапласа m раз, снова придем к полигармоническому уравнению ( m + n ) -го порядка, которое также может быть представлено в виде системы уравнений (9). Таким образом, из системы уравнений (12) можно одновременно найти значения искомых функций u j и v J в контрольных точках.
Значение функции v ( z ) в произвольной внутренней точке области находится из равенства (9) при е = 1 .
-
4. Граничные условия
В обоих случаях решение сводится к решению уравнения (11), для которого необходимо определить ( m + n ) граничных условий. Они могут быть следующего вида:
1) u| д t = u о ( s ), A u |д т = u 1 ( s ),
An+m-1 I / u |дT = un+m-1(s)> s - дуговая координата на границе;
|
2) i u д n д T 5a " + m - 1 u |
( \ дА u f A = q 0 ( s ), , = q 1( s ), д n д T = q n + m -1( s ); д T |
|
д n |
-
3) смешанные условия, когда на одной части границы заданы uJ , а на другой qJ .
Приведенные граничные условия аналогичны условиям Дирихле и Неймана.
Например, в случае решения задачи об изгибе пластины, жестко защемленной по краям, моделируемой дифференциальным уравнением (1), краевые условия имеют смешанный тип [18]:
I л 5 u u • т = 0 .n
= 0.
д T
Так как граница пластины и нормаль жестко фиксированы, то первое граничное условие показывает отсутствие прогиба на границе, второе граничное условие показывает отсутствие изменения положения края пластины от своего первоначального [16].
При переходе к системе уравнений (12) будут определены ( n + m ) N значений UJ , k , или Q j , k , или частично U J , k и Q j , k . Для задачи 1-го типа достаточно задать nN значений в контрольных точках, дополнительные mN условий могут быть найдены из заданной функции v ( x , y ) в области T и, следовательно, на границе д T :
d(A lv) . ,
un+1 =A u = Av, qn+1 = ——, 1 = (0,m- 1). д n
Для задач 2-го типа nN значений в контрольных точках определяются из граничных условий для первого уравнения системы (4), а оставшиеся mN значений - из граничных условий для второго уравнения этой системы.
-
5. Оценка точности численного алгоритма
Оценить точность данного численного алгоритма возможно, оценив погрешность вычислений. Значение искомой функции u ( z ) в каждой внутренней точке области T определяется формулой (8) при е = 1 .
Абсолютное значение разности интегралов в (8), вычисленных по контуру дT области T и по границе L вписанной многоугольной области D , рассчитываем следующим образом:
n - J -1 n - J -1
Е f ( q j + pgp - uj + php ) ds -E f ( q j + pgp - u + php ) ds p =0 а т p =0 l
По теореме о дивергенции [19], справедлива следующая оценка:
— j -1
Е Кq,.pgp — jphp)ds— p=0 at hi
2 .2
. [ Y," (0) — ds . ... = Y, (0) h . O ( h 3).
h i -^ --
Тогда
—
n — j —1
Е f( q , . A
—
p =0
L
u , . , H , ) ds -
c- p ■ max ( y i (0) ) . O ( h 2 ) ,
n — j —1
)j ( A u , . p G p
D
n — j —1
- Е ]J|(A uj. pgp — uj. p A Gp) d t- p=0 T—D
- Е Mp ■c- nM c , (13)
p =0
где h = p / N , p - периметр вписанного многоугольника. Таким образом, расположение контрольной точки в середине хорды при вычислении интегралов типа (6) допускает ошибку O ( h 2 ). С другой стороны, с учетом условия Гельдера
I c i l =
hi j Y i (s) ds hi
—
- max | y, (s) | h - AhX41, sе[— hi/2,hi/2] i i i
где c - площадь области T — D ; Mp - наибольшее значение модуля |(Au,.pGp — u,.p AGp )| в этой области; M = max M . Таким образом, погрешность прямо про-pp порциональна площади c . Оценим ее.
Представим площадь области между контуром и вписанной многоугольной областью c в виде
N c = Е ci, где ci - площадь i-го сегмента между грани-i=1
цей и i -й хордой, i = 1, N .
Введем с центром в контрольной точке каждой i -й хорды локальную систему координат так, что ось Os совмещена с хордой, s е [ — h i / 2, h i 1 2 ] . Тогда разложение некоторой функции f ( s ) в окрестности нуля в ряд Тейлора имеет вид
5 2
f ( s ) = f (0) . f '(0) s . f "(0) у .
. f "(0) s- . f ""(0) s - .... (14)
6 24
Отсюда производная определится следующим образом:
f .(0) = f (V2) - / ( - h i /2) . O ( hi
Площадь сегмента c i как площадь некоторой криволинейной трапеции, образованной кривой y i ( s ) и хордой, c учетом (14) и (15) рассчитывается так:
hih i h i
2 22
c i = j y i ( s ) ds = j y i (0) ds . j y ‘ (0) sds .
—hL — hL
2 22
где
A
i
- постоянная Гельдера; 0
Для площади c справедлива следующая оценка:
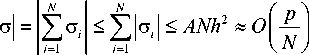
где А = max Д . Из (13) понятно, что погрешность пря-i мо пропорциональна площади c . При неограниченном увеличении количества узлов N ^ да площадь c ^ 0, следовательно, погрешность также стремится к нулю, и возрастает точность предлагаемого численного метода.
-
6. Численные примеры
Пример 1. Рассмотрим тонкую пластину толщиной 0,003 м эллиптической формы с полуосями а = 1, b = 0,6 м в недеформированном состоянии на плоскости Oxy , края которой жестко закреплены. На поверхности пластины распределена безразмерная линейная внешняя нагрузка q = 100(1. x).
Рассчитаем функцию изгиба.
Решаем уравнение
A 2 u = q
в
R T Jr x2 У2 I области t = < (x, y) —.---1), если на контуре I 1 0.36 I пластины dT граничные условия имеют вид du u|-T = °- ^n
= 0.
S T
Применяя описанный выше алгоритм, переходим к системе матричных уравнений
( 0.5 E + H o ) U i - G O Q 1 - G 1 Q 2 = - H 1 U 2 , H 1 U 1 - G . Q . - G 2 Q 2 = - H 2 U 2 , G 0 Q 2 = ( 0.5 E + H o ) U 2 .
Форма прогиба пластины представлена на рис. 2, линии уровня на рис. 3.
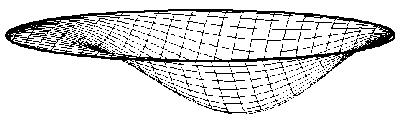
Рис. 2. Форма прогиба эллиптической пластины
Fig.2. The shape of the deflection of elliptical plates
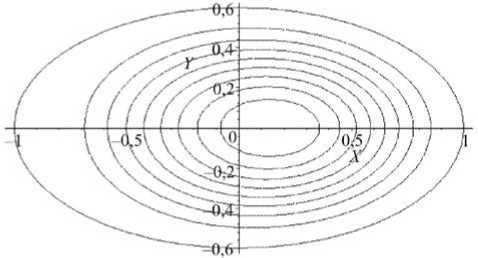
Рис. 3. Линии уровня при изгибе эллиптической пластины
-
Fig. 3. Level lines when bending an elliptical plate
Пример 2 . Рассмотрим тонкую пластину толщиной 0,003 м квадратной формы T = { -0,5 < x < 0,5, -0,5 < y < 0,5 } в недеформированном состоянии на плоскости Oxy , края которой жестко закреплены. На поверхности пластины распределена безразмерная внешняя нагрузка, которая удовлетворяет гармоническому уравнению. На границе нагрузка принимает следующие значения:
q\x = ± 0 , 5 = 100(1,25 - y 2), q\y =±0,5 = 100 ( 0,75 + x 2 )-
Рассчитать функцию прогиба.
Для численного решения перейдем к полигармони-ческому уравнению третьего порядка с граничными условиями u = 0, d T d n 8 t
A 2 u = 100(1,25 - y 2 ),
I x =±0,5
A 2 u | + o5 = 100(0,75 + x 2 ).
Решение этого уравнения на границе сводится к решению системы линейных алгебраических уравнений:
G 0 Q 0 + G 1 Q 1 + G 2 Q 2 = ( 0.5 E + H 0 ) U 0 + H 1 U 1 + H 2 U 2 ,
< G 0 Q 1 + G 1 Q 2 = ( 0.5 E + H 0 ) U 1 + H 1 U 2,
[g 0Q2 =( 0.5E + H 0) U2, которую можно свести к простому матричному уравнению
|
[ G 0 |
G 1 |
G 2 1 |
^ Q o 1 |
" ( 0.5 E + H 0 ) U 0 + H 1 U 1 + H 2 U 2 " |
||
|
0 |
G 0 |
G 1 |
Q 1 |
= |
( 0.5 E + H 0 ) U 1 + H 1 U 2 |
|
|
_ 0 |
0 |
G 0 _ |
_ Q 2 _ |
( 0.5 E + H 0 ) U 2 |
Результаты построения функции прогиба u представлены на рис.4
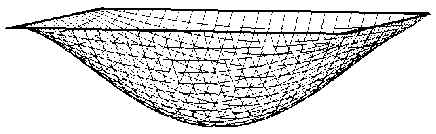
Рис. 4. Форма прогиба квадратной пластины
-
Fig. 4. Square plate deflection
Заключение
Изложенный численный алгоритм построен для системы упрощенного вида, но может быть применен к широкому классу подобных систем уравнений и представлять теоретический интерес для научных коллективов. В работе решена задача об изгибе тонкой пластины с известной нагрузкой, а также задача об изгибе плиты с неизвестной нагрузкой, удовлетворяющей полигармо-ническому уравнению.
В современной научной практике часто методом выбора для численного решения, например, задач механики являются конечно-разностные схемы, метод конечных элементов, вариационные методы [4, 6, 15, 20, 25, 26, 30]. Но они учитывают все дискретные точки области. В ряде задач теории упругости требуется вычисление производных. Например, при решении классической задачи теории упругости для функции Эри нахождение напряжений требует численного вычисления производных. В указанных методах необходимо использование не только граничных точек, но и внутренних точек области. В сравнении с ними метод граничных элементов учитывает только точки на границе, что повышает точность расчетов. В работе оценена точность метода, эффективность метода подтверждена в более ранних работах [8, 9, 13, 14] на различных примерах сравнением численных результатов и аналитических решений.
Список литературы Краевые задачи для неоднородных систем полигармонических уравнений с приложениями в теории тонких оболочек и пластин
- Бенерджи П., Баттерфилд Р. Методы граничных элементов в прикладных науках. - М.: Мир, 1984. - 494 с.
- Бреббия К., Телес Ж., Вроубелл Л. Методы граничных элементов. - М.: Мир, 1987. - 524 с.
- Векуа И.Н. Новые методы решения эллиптических уравнений. - М.: Физматлит, 1948. - 296 c.
- Векуа И.Н. Некоторые общие методы построения различных вариантов теории оболочек. - М.: Наука, 1982. - 282 с.
- Голушко С.К., Идимешев С.В., Семисалов Б.В. Методы решения краевых задач механики композитных пластин и оболочек / Конструкт.-технол. ин-т вычислит. техн. Сиб. отд-ния РАН. - Новосибирск, 2014. - 131 с.


