Краевые задачи с разрывными граничными условиями для некоторых систем уравнений в частных производных

Системам уравнений в частных производных, в частности эллиптическим, посвящены исследования многих математиков. Интерес к ним обусловлен рядом факторов. Во-первых, многие задачи механики, в частности теории упругости, сводятся к краевым задачам для эллиптических систем уравнений различных порядков, что, естественно, требует их всестороннего изучения. Во-вторых, возможно и во-первых, большое значение имеют чисто теоретические вопросы, в том числе вопрос о корректности тех или иных задач для таких систем уравнений. В данной работе речь пойдет о разрешимости в обобщенном смысле краевых задач для некоторых систем уравнений в частных производных. Идея введения обобщенных решений начала проникать в математическую физику с 20-х годов прошлого столетия. В частности, при исследовании двумерных вариационных задач появилась необходимость расширить класс функций, среди которых ищется минимум, привлекая непрерывные функции, имеющие обобщенные производные (классы Тонелли). Другим источником возникновения обобщенных решений послужили нестационарные задачи для волнового уравнения и уравнений гидродинамики, где давно вводились разрывные решения в виде плоских и сферических волн с сильным разрывом, а также решения, описывающие ударные волны.

В этом направлении значительные и во многом определяющие все дальнейшие исследования результаты получены С.Л.Соболевым. В основу определяемых им обобщенных решений той или иной задачи для уравнения Lu = f положено интегральное тождество J uL vdx = J fvdx, имеющее место для некоторого класса гладких «пробных» функций. Затем доказывается, что такие обобщенные решения дифференциальных операторов с постоянными коэффициентами по существу являются пределами, в том или ином смысле, гладких решений исследуемых задач. Таким образом, С.Л.Соболев приходит к другому определению обобщенных решений уравнения Lu = f, как пределу классических решений. В настоящее время эти два вида обобщенных решений называются слабыми и сильными решениями.

О.А. Ладыженская [1], продолжая исследования в указанном направлении, отметила, что для каждой задачи можно вводить различные классы обобщенных решений, определяе- мые тем функциональным пространством, к которому принадлежит искомое решение. При этом оказалось, что корректность задач зависит от функциональных пространств, в которых ищется решение. В свою очередь, отметим, что корректность задач для одного уравнения существенно зависит от типа этого уравнения.

Автора в первую очередь заинтересовал тот факт, что системы уравнений в частных производных существенно отличаются от одного уравнения с точки зрения постановки корректных задач, чего нет в случае обыкновенных дифференциальных уравнений . В частности, если для одного эллиптического уравнения второго порядка корректной является задача Дирихле, то хорошо известен пример эллиптической по Петровскому системы уравнений второго порядка, для которой нарушается единственность решения задачи Дирихле [2].

Приведенную в работе А.В.Бицадзе [2] систему уравнений запишем в комплексной форме

д u = о

дz2     ’ где z = x + iy, u (=) u1(x, y) + iu2(x, y),

д 1

д

z

2 кд x

^1

^д y )

Любое классическое решение уравнения (1) есть функция u(z) = ф(z) + z^(z), где ф(z),^(z) - произвольные аналитические функции. Поэтому в круге |z| < в для У в > 0, полагая у(z) = —zф(z) и убирая постоянный множитель, получаем бесконечное множество рев в шений u(z) = ф(z) (в2 - |z|2), обращающихся в ноль на окружности |z| = в . Это свидетельствует о том, что задача Дирихле для системы уравнений Бицадзе некорректна.

В данной работе зададимся целью найти такие постановки краевых задачах для системы уравнений (1), которые имеют однозначную разрешимость в пространствах Соболева.

Обозначения

д

Пусть в дополнение к введенным ранее обозначениям — = д z

д . д ) n i, а D

2 кд x д y у

- область

на комплексной плоскости с достаточно гладкой границей Г , n = n 1 + in ₂ - единичный вектор внешней нормали к Г .

При изучении краевых задач нам потребуются следующие функциональные простран-

ства: пространство L ₂ ( D ) со

скалярным произведением

||u\ |₀ = \( u , u ) ₀ ; пространства

Соболева    W™ ( D )   со

( u , v ) ₀ = Re j uvdD и нормой

D скалярным произведением

, х _n                д k u д k v

^{( u} , ^v ) m = ^Rel ^{uv +} £ ^T" ы дx k

m

д k u д k v

D

k = 1

к

----;—I--т~ *----7" д x k    д y k д y k _у

dD и нормой

II ^u L = 4 ^{( u} , ^u ) m ; пространства

функций, имеющих непрерывные частные производные, Сm (D), Сm (D), m < ^ , то есть, например, u(z) e Cm(D), если u 1(x,y),u2(x,y) e Cm(D); обобщения этих пространств, связан- д     д

.

ные с операторами — и — a z      д z

Для функций u(z), v(z) e C*(D) имеют место формулы интегрирования по частям f ^ vdD = Л D дz j f ^ vdD = 4 D дz j

■ д v u

. дz д v

u дz

,        1 f

■ dD + — uvnd r , 2^J

г

. 1 f dD + — uvndr, 2 J

г

которые справедливы и в пространстве W ^ ( D ). Кроме того, нам понадобится формула

дu д и дz дz

и следствия из нее, которые будут приведены по мере необходимости.

Всюду в тексте черта над комплексным выражением обозначает комплексное сопря жение, а над множеством - его замыкание.

Задача Римана-Гильберта для обобщенной системы уравнений Коши-Римана

Поскольку оператор в системе уравнений Бицадзе (1) является второй степенью оператора Коши-Римана, представляется вполне естественным найти и исследовать сначала корректные постановки краевых задач для системы уравнений Коши-Римана, а затем дополнить краевые условия до условий для системы (1).

В области D рассматривается уравнение

ди.

Lu = --+ a ( z ) и + b ( z ) и = f ( z ),                       (5)

дz где a (z) = a i( x, y) + ia 2( x, y ), b (z) = bi( x, y) + ib 2( x, y ), f (z) = f1( x, y) + if,(x, y) - заданные функции.

Уравнение (5) является комплексной формой обобщенной системы уравнений Коши -Римана [3].

Разобьем границу области на части следующим образом

Г+ = {z еГ | п1 > 0}, Г- = {z еГ | п1 < 0}, Г0 = Г\(Г+ U Г-).

Задача 1. В области D найти решение уравнения (5) при условиях и 1 |Г-иГ0 = и2 |Г+ = 0.                                        (6)

По существу, задача 1 является обобщенной задачей Римана-Гильберта [3] с разрывными граничными условиями. Действительно, условия (6) можно записать в виде

(a( x, y) и + в( x, y) и 2 )|г = 0, где

a ( x , y )

<

'1,( x , y ) еГ^- U Г ⁰

0, ( x , y ) еГ⁺

и

^{e ( x} , y )

<

'0, ( x , y ) еГ^- U Г ⁰

1,( x , y ) еГ⁺

являются разрывными функ-

циями.

Эта задача и теоремы о ее разрешимости без доказательства приведены в работе Б.Б. Ошорова [4]. Здесь предлагаются достаточно подробные доказательства.

Множество функций и ( z ) е C ” ( D ), для которых выполнены условия (6), обозначаем через C_L , а его замыкание в норме ||-| |1 - через H_L . Очевидно, что H_L с W .' ( D ).

Лемма 1. Для любой функции и ( z ) е H_L имею место оценки

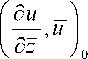
> 0 ,

д и

5 z 0

= Ы 10+Iki 12-

Доказательство. Достаточно получить эти оценки для любой функции и(z) е СL . Ин- тегрируя по частям, согласно формуле (2), получаем

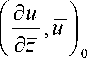
= — j и ² n,d Г

⁴ Г +

= Re J ^^dD = 1Re J и ² nd Г = ¹ J [( и ²

D ^д z ⁴ Г           ⁴ Г

- и ² ) n 1

- 2 и 1 и ₂ n ₂ ] d Г =

-

J и 2 n 1 d Г >  0.

Г

Далее

д и д z

д и д и

= Re--. o      D д z д z

-dD = 1 j [( и 1 x — и 2 у ) ² + ( и 2 x + и 1 y ) ² ] dD = 4 _D

= vj ^{( U} 1 x ^{+ и} 2 x ^{+ и} 1 У ^{+ и} 2 У 4 _D

—

^{2 U} 1 x ^U 2 y + ^{2 U} 2 x ^U 1 y ) ^dD •

Пользуясь обычной формулой интегрирования по частям, получаем

D где т = — n2 + in

j ^и 1 x^u 2 y dD = ^—

D

= j ^и 1 y^u 2 x dD +

1 2 xy                 1 2 y 1                 1 y 2 x                 1        2 x 2        2 y 1

D             Г                D              Г

[ и ] ^^^ dD, j 1 д т

— единичный касательный вектор к границе Г .

В силу условий (6)

j и x г

^ 12- ^dD = ^o, j ^u 1 x ^u 2 y ^dD = j ^u 1 y ^u 2 x ^{dD дТ}            D            D

и

д и д z

= j ^{( U} 2 ^{+ U} 2 x ^{+ U} 1y ^{+ U} 22 y ) ^dD = || ^U x | |_o ^{+ U} y ||_o • D

Лемма 2. Если     а ( z ), Ь ( z ) e C ( D )   и матрица A =

f b , + a ,

I a 2      b 1

a 2

—

^а 1 )

положительно

определена в области D , то для любой функции и ( z ) e H_L имеет место оценка ||Lu ||_o >  c||u ||_o , c = const >  o.

Доказательство. Неравенство (9) является следствием оценки (7), так как д и

( Lu , и )₀ = (— , и )₀ + ( аи + Ьи , и )₀ >  ( аи + Ьи , и )₀, ( аи + Ьи , и )₀ = ^o д z                                 v                      v              ,°

= j [(Ь1 + a 1)U12 — 2 a 2 U1 U 2 + (Ь1 — a 1)U 2] dD > c|U| ^ Ц |o = Ц |o, (LU, U )o > c|U| C D откуда в силу неравенства Гельдера следует оценка (9).

Лемма 3. Если для функций а ( z ), Ь ( z ) e C ( D ) существует достаточно малое число а >  o, такое, что | аи + Ьи | < а | и | (степень малости уточняется по ходу доказательства), то для любой функции и ( z ) e H_L справедлива оценка

II Lu lo >  ^С Н

Доказательство. По свойству нормы

1 ,

c = const >  0 .

||Lu\ |_o = d u + a ( z ) и + b ( z ) и >

д и д z

^— I a ^{( z} ) ^{u + Ь ( z} ) ^u ll_o >

д и д z

—

a l u llo.

В силу простейшей теоремы вложения для функций и ( z ) e H_L имеет место неравенство

II ullo < в( ux\lo + И Io )= в

д и

^{д z} 0’

где в = const зависит от mesD .

Отсюда имеем неравенство || Lu ||_o >  (1 — ар )

д и д z

, где а должно быть столь малым, 0

чтобы выполнялось неравенство 1 — ав >  0.

Из равенства (8) и неравенства (11) следует, что в пространстве H_L норма

5 u

5 z

экви-

валентна норме u ₁ , поэтому имеет место оценка (10). Лемма доказана.

Отметим, что в условиях леммы 3 можно положить либо a ( z ) = 0, либо b ( z ) = 0, либо a ( z ) = b ( z ) = 0 .

Далее, для произвольных функций u ( z ) e H L , v ( z ) e C ” ( D ) рассмотрим выражение f 5 u ) _ы

I ——, v I . Интегрируя по частям, получаем

V ^{5 z} ) о

5 u i _ г 5 u _ г 5 v 1 _ г _ _     _ г 5 v 1 гг, .

—, v I = Re [ —vdD = - Re [ u — dD + — Re \ vnddT = - Re [ u— dD + — [[( u 1 v 1 + u 2 v 2 ) n + 5 z ) ₀       ^J 5 z             ^J 5 z       2 *                J 5 z      2 *

1 f   5 v |    1 f _ 1 r _ 1 r _ 1 r _

+ ( u 1 v ₂ - u ₂ v 1 ) n ₂ ] u 1 d r = -I u ,— I + — u 1 v 1 n d r + — u ₂ v ₂ n d r + — u 1 v ₂ n ₂ d r— u ₂ v 1 n ₂ d r = V ^{5 z} ) 0 ² Г +             ² A             ² Г +             ² г - U. 1

f 5 v I 1 г z           .„-1c,

-I u ,— I +— I u 1 ( v 1 n + v ₂ n ₂ ) d r + — I u ₂ ( - v 1 n ₂ + v ₂ n 1 ) d r .

^{V 5 z )} 0 ² r ^{+                        2} r ^- U r ⁰

Следовательно, во-первых, оператор

—

5 I A

— I является формально сопряженным для 5 z )

5                         _ оператора , во-вторых, если потребуем для функции v(z) выполнение условий 5z v 1 nx + v2n2 |r+ = 0, - v 1 n2 + v2n 1 |r-ur = 0 ,

то имеет место тождество

5 u I     f 5 v I

—, v I = -I u ,— I .

.^{5 z}   ) 0      V    ^{5 z} ) 0

Условия (12) заведомо выполнены для функций v ( z ), если ^v 1 lr = ^{v 2}1 r ⁺ U r ^- = ⁰ .

Если же D = {z | 0 < x < k, 0 < y < h} - прямоугольник, то условия (12) равносильны услови- ям v 11 r+ ur0 = v2 I r- = 0.                                       (15)

Для оператора L формально сопряженным будет оператор, который задается формулой

,      5 v ——t        _

L * v =--- + a ( z ) v + b ( z ) v

5 z

Множество функций v ( z ) e C ” ( D ), для которых выполнены условия (12), а в случае прямоугольника - условия (15), обозначаем через C L* , а его замыкание в норме ||-| |1 - через ^H L * ^.

Из тождества (13) следует, что для функций u ( z ) e H L , v ( z ) e H L * выполняется равенство

( ^Lu , ^v ) ₀ = ( ^u , ^L * ^v ) ₀ .                                   ⁽¹⁶⁾

Определение 1. Функция u ( z ) e L ₂ ( D ) называется слабым обобщенным решением задачи (5),(6), если для любой функции v ( z ) e H L * имеет место тождество

^{( f} , ^v ) 0 = ^{( u} , ^L * ^v ) 0 ^.

Для функций v ( z ) e H L * справедливы следующие утверждения.

Лемма 1*. Для любой функции v ( z ) e H L * имеют место оценки

Лемма 2*. Если

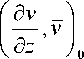
-1Ы 10

d v d z

a ( z ), b ( z ) e C ( D ) и

< 0 ,

+1 H 12.

(7*)

(8*)

матрица A -

( b l ⁺ a l

I ^a г

a 2

b l - a l )

положительно

определена в области D , то для любой функции v ( z ) e H L * имеет место оценка

||L * v ||₀ >  c||v ||₀ , c - const >  0.                                   (9*)

Лемма 3*. Если для функций a(z),b(z) e C(D) существует достаточно малое число a > 0, такое, что | av + bv |< a | v |, то для любой функции v(z) e HL* справедлива оценка || L * v||0 > c||v||., c - const > 0.                                 (10*)

Доказательство этих лемм практически совпадает с доказательство лемм 1 - 3.

Теорема 1. Если выполнены условия леммы 2* или леммы 3*, то для любой функции f ( z ) e L ₂ ( D ) существует слабое решение задачи (4),(5).

Доказательство. Для фиксированной функции f ( z ) e L ₂ ( D ) и произвольной функции v ( z ) e Н _L * рассмотрим выражение ( f , v ) ₀ . Согласно неравенству Гельдера и оценок (8*) или (9*) получаем

I(f,v)0| <1 f|,|v||0 < m||f|,|L *v||0, то есть (f, v)0 является линейным ограниченным функционалом по L * v над некоторым под пространством пространства L2(D). По теореме Хана - Банаха продолжаем этот функционал на все пространство. Тогда по теореме Рисса о представлении функционалов в гильбертовом пространстве найдется функция u(z) e L2(D), такая, что имеет место равенство

^{( f} , ^v ) 0 ^{- ( u} , ^L * ^v L

Теорема доказана.

Теперь исследуем разрешимость поставленной задачи в пространстве W₂(D ).

Как было сделано в работе [5], введем негативные пространства, которые подробно описаны в монографии [6]. На функциях f ( z ), g ( z ) e L ₂ ( D ) определим нормы

II ^gW - 1 - sup u e Hl

( g,u )0

I h - 1

sup

^{( f} , v ) 0

v e Н L *

Замыкания пространства L ₂ ( D ) по нормам ||-|| _н и ||-|| _н . называются пространствами Н - 1 и

Н -. , соответственно.

Из определения негативных пространств следует

L , ( D ) с H . 1 , L , ( D ) с H - . .

Известен аналог теоремы Рисса о представлении линейных непрерывных функционалов над негативными пространствами.

Лемма 4. Если над пространством Н - . ( Н . . ) задан линейный непрерывный функционал l ( f ) ( l ( g )) , то существует функция v ( z ) e H_l * ( u ( z ) e H_l ), такая, что l ( f ) - ( f , v ) 0 , ( l ( g ) - ( g , u ) 0 ).

Доказательство этой леммы можно найти в той же книге [6].

Лемма 5. Если выполнены условия леммы 3*, то для любой функции v ( z ) e Н . справедливо неравенство

II Lv   —

- 1

> c||v ||₀ , c = const >  0 •

Доказательство. Рассмотрим в области D вспомогательную задачу

5 u        _       _

— = v , v ^e C L * , ^{U e C} L •

dz

Как известно [3], решение уравнения (18) имеет вид u ( z ) = Ф ( z ) — ~( z ), где Ф ( z ) —

произ-

вольная аналитическая функция в области D , а ~( z ) = — [ v^{( Z} \ П D Z — Z

—

dzdn, Z = £ + in •

В качестве Ф ( z ) возьмем решение задачи

"d z" = 0, ^ф|_г ^— и г ⁰ = и| г — и г ⁰, ^ф|_г+ = и\ _г+ , которая называется смешанной краевой задачей аналитических функций и представляет собой частный случай задачи Гильберта с разрывными коэффициентами [7],[8]

Таким образом, задача (18) имеет решение и e C_L для любой функции v e C_L * .

Из доказательства леммы 3 следует, что существуют    c 1 , c ₂ = const >  0,

такие, что c J| u ||1 <

d u d z

< c ₂ || u ||1 для любой функции u e C_L • Тогда для решения задачи (18)

имеет место неравенство

с1 lulI < IM L

Далее, согласно тождеству (16) и неравенству (10), получаем

Lu, — | =(Lu,Lu — au — bu)₀= |LU|2 —(Lu,au + bu)₀>c₃||u||2, c₃ = const>0, az)0                                                ^{110                                        111}

(L* v, u )0 =( Lu, v )0 =

откуда следует неравенство

IL 4— >c «IML- и, наконец, в силу неравенства (19) -

IILAL.,>cllvlL c=const>0

Теорема 2. Если выполнены условия леммы 3, то для Vf (z) e L₂(D) существует единственное слабое обобщенное решение задачи (4), (5) u(z) e HL.

Доказательство. Рассмотрим выражение (f, v)₀для Vv(z) e HL*. Тогда в силу неравенства (16)

I⁽f,^v )0l <1 IflU М L < ^mW\LIL* AL_—, то есть (f, v)₀является линейным непрерывным функционалом по L*v над негативным пространством H_—1. По лемме 4 3 u (z) e H 1, такая, что

⁽f,^v)0 = ^(u,^L*^v)0, ^Vv(z) ^{e H}( •

Интегрируя по частям, получаем

⁽f, ^v)0 =^(Lu, ^v)0, ^Vv(z) ^{e H}L*, то есть Lu = f почти всюду в D•

Единственность следует из неравенства (9), которое для решений задачи (5), (6) можно записать в виде

II^ulli < ^{c 1} Ifllo, ^c = const > ⁰.

Аналоги задачи Римана-Гильберта

Обратим внимание на то, что всюду выше нигде не использовалась эллиптичность по Петровскому, которая для системы уравнений

Lu = У AaD u + Tu = f a a

|a| =m определяется условием

Q (X) = det

Z AX

|a|=m

* 0,

VX * 0.

Отсюда возникает предположение, что условие эллиптичности по Петровскому не является существенным для корректности задач, подобных задаче (5), (6).

Действительно, выбрав в качестве области на плоскости прямоугольник

D = {(x, y) e R2: 0 < x < k, 0 < y < l}, рассмотрим модельные системы уравнений вида

LmU = AUx + BUy + CU = F (x, y),                 (20)

где m означает размерность вектор-функции. Если m = 2 и

A =

(-1 01

< 0 1),

B =

I1 0 ) ’

то система уравнений (20) представляет собой матричную симметрическую запись обобщенной системы уравнений Коши-Римана (5), а характеристическая форма имеет вид det (AX1+ BX2= -(X2 + X2).

При m = 3 полагаем

	(-1	0	0 1		( 0	1	01
A =	0	1	0	, b =	1	0	-1	.                          (21)
	1 0	0	-1;		10	-1	0;

В этом случае характеристический детерминант задается формулой

det( AX1 + BX2 ) = X то есть система уравнений (20), (21) по классификации Петровского не имеет определенного типа.

Если же m = 4 и

(-1

A =

I 0

0	0	01	(0	1
1	0	0	. 1 , в =	0
0	-1	0	0	-1
0	0	1;	10	0

-1

то

det(AX + BX2) = (X2 + X2)2 + X2X2 > 0, то есть система уравнений (20), (22) эллиптическая в любой области D с R2.

Задача 2. В прямоугольнике D найти решение системы уравнений (20), (21) при гра- ничных условиях u1( x ,0) = u1( k, y) = u 2(0, y) = u 2( x, l) = u 3( x ,0) = u 3( k, y) = 0.             (23)

Задача 3. В прямоугольнике D найти решение системы уравнений (20), (22) при гра- ничных условиях u1( x ,0) = u1( k, y) = u 2(0, y) = u 2( x, l) =

= u₃( x ,0) = u₃( k, y) = u₄(0, y) = u₄( x, l) = 0

Лемма 6. Если матрица С(x, y) e C(D) положительно определена в D, то для любой вектор - функции U(x, y) e C” (D), удовлетворяющей условиям (7) при m = 3 или условиям (8) при m = 4 , справедливы неравенства

(LU,UX > 8UI 12, ||LmU||₀> 8|UI|₀, 8 = const > 0.

Доказательство этой теоремы проводится интегрированием по частям.

Такие же неравенства имеют место для формально сопряженного оператора Em на век-тор-функциях V(x, y) е C” (D), удовлетворяющих естественным образом заданным сопря- женным краевым условиям.

Отсюда следует, что поставленные задачи имеют, по крайней мере, единственные слабые обобщенные решения из пространства L₂(D), которые совпадают с сильными решениями, а для классических решений этих задач справедлива теорема единственности.

Далее рассмотрим трехмерное пространство R³. Для системы уравнений первого порядка, когда искомая вектор-функция имеет такую же размерность, характеристическая форма имеет нечетный порядок

Q (2) =^ ааХ“х' 2 2?,

1 а=3

где a = (a1,a₂, a₃) - мультииндекс, |а| = а_х + а₂+ а₃. Эта форма априори не может быть знакоопределенной.

Тем не менее, и в этом случае можно привести примеры систем уравнений первого порядка, которые можно считать аналогами систем уравнений на плоскости с точки зрения по- становок краевых задач.

В параллелепипеде

D = {x = (x 1, x2, x3) е R3 : 0 < xt < k t, i = 1,3 } рассмотрим симметри- ческую систему уравнений

LU = £BUx_+ B(x)U = F(x), i=i где

(1 0 0 ^

-1

B1 =⁰-¹⁰

( 0 0 1J

B 2

-1   0   0

_v0    0   a_{2 v}

B 3

' a^{3 0 0}"

0   0 1

< 0 10 v

a i = const, i' = 2,3.

Для этой системы уравнений

+ a₃21 2₃+ 2²₂)-a₃2₃(22 + 22 )

Q(2) = -21 £ 22 - a222 (22

i=1

что не дает возможности определить ее тип. Отметим только, что при a2 = a3 = 0 мы имеем систему составного типа.

Задача 4. В параллелепипеде D найти решение системы уравнений (25) при условиях U\\ п = ^Мз| п = U2I ъ = 0,

¹ lx! =0         ³ lx! =0         ² lx! = k!

U2I n = Uli t = U3L    m = 0,

² Ix2=0        ¹ lx2=k2         ³I(a2п2<0)

U3I n = U2I t = U1L    m = 0,

³ lx3=0        ² lx3=k3         1I(a3п3<0)

где n = (n1, n₂, n₃) - единичный вектор внешней нормали к Г.

Сопряженная задача 4*. В области D найти решение системы уравнений

LV ^-^ В^+ B* (x)V = G(x), i=1

при условиях v 11 x, = k 1 = v з| x, = k 1 = v 2I x, =0 = vJ     = v, I     = v, |        =

2 Ix2=k2        1 lx2=0        3I(a2п2>°)’ vj     = Vil    = v.|       =

31 x3 = k3        ² lx3 =0        1I(a3пз>0)

Постановка задачи 4, с точностью до размерностей пространства и искомой вектор -функции, совпадает с постановками задач 2 и 3. Поэтому ограничимся формулировкой леммы.

Лемма 7. Если матрица B(x) e C(D) положительно определена в D, то для любой вектор - функции U(x) e S (г(x) e SL. ) справедлива оценка

ILU\10> 81U10 (|\Eг|10> 81П| ), 8 const > 0.

Здесь через SL (SL) обозначены классы гладких вектор-функций, удовлетворяющих краевым (сопряженным краевым) условиям.

Эта лемма позволяет утверждать, что задача 4 также имеет единственное слабое обобщенное решение из пространства L₂(D) , которое совпадают с сильным решением, а для классических решений этих задач справедлива теорема единственности.

Задача Пуанкаре для обобщенной системы уравнений Бицадзе

Теперь в области D рассмотрим уравнение второго порядка

Mu J^-u + Ku = f (-),

dz²

которое является комплексной формой эллиптической системы уравнений второго порядка, названной обобщенной системой уравнений Бицадзе. Корректность задачи Дирихле для уравнения (26) зависит от оператора K [9], [10].

Считаем, что D - произвольная ограниченная область на комплексной плоскости с достаточно гладкой границей Г, которая разбита на части, как в случае задачи 1. Рассмотрим задачу, в которой к условиям задачи 1 добавлены новые краевые условия.

Задача 5. В области D найти решение уравнения (26), удовлетворяющее условиям

u 1 Ir-_Ur0 = u2 lr+ = Re uz Ir-_Ur0 = Imuz lr+ = ⁰.

Для исследования поставленной задачи введем некоторые понятия.

Сначала отметим, что для любой функции v(z) e C1(D) IC(D), v |_r= 0, формулы (1) и (2) принимают вид

ju_zvdD = -Juv_zdD, Ju_zvdD = -Juv_zdD.

D

D

D

D

Класс таких функций v(z) обозначаем через C₀¹(D) .

Определение 2. Функция w(z) e L₂(D) называется обобщенной производной функции u(z) e L₂(D) вида и- или u_z, если для любой функции v(z) e C0(D) имеют место тождества juv_zdD = -J wv dD или juv_zdD = -J wv dD , соответственно.

D

D

D

D

Для обобщенных производных мы сохраняем такие же обозначения, как и для обычных производных, то есть w = u- или w = u_z.

Пусть теперь u(z), v(z) e C2 (D) IC1 (D). Используя формулы (1) и (2), получаем juzzvdD = - juzvzdD + — juzvndr =juvzzdD + — j(uzv - uvz)nd? ,

D           D          2 Г         D juzzvdD = - juzvzdD + — juzvndr =juvzzdD + — j(uzv - uvz)ndr,

D           D          2 Г          D f u-vdD = - f uv-dD + — f uvndr = f uv-dD + — f (uvn

- uvzn ) dr =

zz                  z z                 z                  zzz

D           D          2 Г         D

Г                 . 1X

= uv-dD + — (u-vn - uvn) dr.

zz                  zz

D

Класс функций v(z) e C2 (D) IC 1(D), для которых выполнены условия v |Г = vz |Г = 0, будем обозначать через C02 (D). В этом случае juzzvdD = -juzvzdD = juvzzdD .

D

D

D

Для класса функций v(z) e C 2(D) IC 1(D) = C02(D), которые удовлетворяют условиям v |Г= vz |Г= 0, выполнено равенство juzzvdD = -juzvzdD = juvzzdD.

DD

Если же v(z) e C₀²(D) или v(z) e C₀²(D), то j u_zz^vdD = j

D

D

uv_zzdD.

D

Определение 3. Функция w(z) e L2 (D) называется обобщенной производной функции u(z) e L2(D) вида uzz , если для Vv(z) e C02(D) имеет место тождество j wvdD = juvzzdD.

D

D

Аналогично определяются обобщенные производные вида u_zz и u_zZ, а также производные более высоких порядков.

Впрочем, во всех определениях в качестве класса “пробных” функций можно взять множество C 0 (D) = {v (z) e C^k (D) I C^k-1( D )| | d^Jul | _г = 0, l = 1,2, j = 0, k -1}. Очевидно, что C₀^k (D) является подмножеством для всех приведенных ранее классов “пробных” функций.

Через W’k (D) обозначаем множество функций u(z) e L2(D), имеющих обобщенные a ju _                   n_ производные —- e L2 (D), j = 1, k, W20 (D) = L2 (D). В этом пространстве скалярное произве-azj                          2

дение и норма задаются формулами

(u,.)k = RejfVAD, ИC’ =(u, u)HZ Dj=o az azj       ^k          j

k, a^j

u

az^j

dD,

^{а (u},^v)0 =^(u,^v)o, ||^u| 10 = lulIo.

Точно так же вводится пространство W’ (D) со скалярным произведением (u,v)‘ = Re f V ^u.^vdD

, )k     j 5zj azj и нормой

k

II ^u lit²= ⁽u,u)k = jz

Dj=0

∂ ^ju ∂z ^j

dD,

при этом (u,v)0 = (u,v)₀, || u IIO = || u ||₀. В случае области D, звездной относительно некоторого круга, пространства W₂^к (D) и W₂^к (D) получаются замыканием пространства С” (D) в соответствующих нормах.

Нетрудно показать, что для любой функции u(z) е W₂^k (D) выполнены неравенства || u ||k< c || u ||_k и || u Ilk< c || u ||_k, где c = const > 0 зависит только от области D и числа к, поэтому имеют место вложения W₂^k (D) с W₂^к (D), W₂^к (D) с W₂^k (D).

Приступим к исследованию задачи (19),(20).

Теорема 3. Если Ku = a(z)uz + b(z)uz и коэффициенты этого оператора удовлетворяют условиям леммы 3, то для любой функции f (z) е L₂(D) задача (26),(27) имеет единственное решение u (z) е W₂²(D).

Доказательство. Пусть w = u-. Тогда, согласно формуле (4), uz = uz = w . Поэтому задача (26),(27) редуцируется в задачу (5),(6) относительно функции w(z). Эта задача при условиях данной теоремы имеет единственное решение w(z) е W₂1 (D), для которого выполнена оценка ||w||1 < c||f ||₀. Согласно лемме 3 ||w||1 = ||wz||₀, ||u||1 = ||uz ||₀. Значит существует единственное решение задачи (26),(27) u(z), удовлетворяющее неравенствам

_          II“=|L < cfL- luzlI0 < cfL- H0 < clflL- то есть u (z) е W22 (D) .

Точнее, u(z) е W₂1(D) и существует u-(z) е W₂1(D). Теорема доказана.

Теперь рассмотрим случай, когда Ku = a(z)uz + b(z)u .

Множество функций u(z) е C” (D), для которых выполнены условия (20), обозначаем через CM, а его замыкание норме ||-||₂ - через HM . Найдем априорные оценки.

Лемма 8. Если функция a(z) удовлетворяет условиям леммы 3, а b(z) - достаточно малая по модулю функция, удовлетворяющая условиям

(z) = 0, (Re bn. - Im bn. )| = 0, dz                       1            2 lr то для любой функции u(z) е HM имеют место неравенства

II^Mu\L^⁵Iul 12, IM^ulL^NuzzL⁺ИL), ⁵=^const>°.

Доказательство. Рассмотрим выражение

^(Mu, ^uz-z-⁾0 = ⁽uzz, u-zz^^{+ (}uzz, a^u-z)0^{+ (}uzz, ^bu)0 .

Согласно лемме 3 имеет место неравенство

⁽uzz, uzz⁾0^{+ (}uzz, auz)0 ^ \zzz ||0.

Поэтому остается рассмотреть выражение (uzz,bu )₀. Интегрируя по частям, получаем

(uzz, bu )₀= Re j uzzbudD =-

D j uz (b ) zudD =j uzbzudD =0;

D

D

Re J uz (b)z udD - Re j buzdD +—Re j buzundГ;

D                D         ²г

; Re jbu =dD |(uz,buz)₀| < max| b | ||uz|12;

D

Re jbuzundГ = Re j (Reb - i Imb)(Re uz + i Im uz )(Re u + i Im u)(n1 + in₂)dГ =

Γ

Γ

=∫[(RebReu_zReu+ImbImu_zReu-RebImu_zImu+ImbReu_z Im u)n₁-

Γ

-(RebReu_z Imu+ImbImu_z Imu+RebImu_z Reu-ImbReu_z Reu)n₂]dΓ =

=∫Reu_zReu(Rebn₁-Imbn₂)dΓ- ∫Imu_zImu(Rebn₁-Imbn₂)dΓ=0;

Γ⁺                                              Γ^-UΓ⁰

I (u_zz,bu)₀I      D         II u_z II₀².                                           (30)

По теореме вложения uz II0≤mIIuzz II0,                                         (31)

где m = const > 0 зависит от mesD .

Из неравенств (29) – (31) следует

I (Lu,uzz )0 I ≥ IIuzz II20 - mDax |b|II uz•II20 ≥ (1 - max | b | m2)IIuzz II20 =δ I uzz II20, δ> 0, откуда получаем оценку

II Lu II₀≥δI uzz II ₀.                                        (32)

Из неравенства (32) таким же способом, как и в лемме 3, получаются оценки (28).

Теорема 4. Если выполнены условия леммы 8, то для ∀f (z) ∈ L2 (D) существует един ственное решение задачи (26), (27) u(z) ∈ HМ .

Доказательство. Рассмотрим вспомогательную задачу

M~u~ ≡ u~zz + a(z)u~z = ~f (z), ∀z ∈ D, u~(z) ∈ HM , где f (z) = f (z) - b(z)u(z) и u(z) - произвольная функция из HM .

Согласно теореме 3 эта задача имеет единственное решение u~(z) ∈ HL для каждой функции f (z) ∈ L2(D), то есть выполняется тождество

(M^~u^~,v)0 =(f,v)0                            (33)

на некотором замкнутом классе “пробных” функций v(z). Если f (z) ∈L₂(D) , то для

∀u(z) ∈H_M f(z)∈L₂(D). Тождество (33) перепишем в виде

(Mu^~-bu^~,v)₀= (f - bu, v)₀

или

(Mu^~,v)₀+(b(u-u^~),v)₀=(f,v)₀.

Отсюда следует, что существует функция u(z) ∈H_M , для которой выполнено тождество

(Mu,v)0 =(f,v)0, то есть Mu = f почти всюду в области D .

Из оценки (28) следует, что такая функция единственная.

Анализ краевых условий показывает, что задача (26), (27) является задачей Пуанкаре [2] с разрывными краевыми условиями.