Критериальное моделирование процесса центробежного разделения утфеля III кристаллизации

Технологический поток получения товарного кристаллического сахара в продуктовом отделении сахарного завода на одном из заключительных этапов включает обработку в центробежном силовом поле утфеля последней кристаллизации – «желтого» сахара, который идет на растворение или аффинацию и последующую переработку. Причем оттек, получающийся в результате центрифугирования последнего утфеля, отводится в виде конечного продукта – мелассы – субстанции, уже не подлежащей дальнейшей кристаллизации.

При исследовании процесса разделения утфеля III, как и при соответствующей обработке утфелей других кристаллизаций, выделяют одновременно развивающиеся процессы осаждения кристаллов сахарозы на фильтрующей поверхности ротора и отвода оттека из рабочего объема машины.

В последующем кристаллы сахарозы подвергают обработке промыванием водой или сахарсодержащим раствором слоя осевшего на стенке ротора кристаллов сахара, его просушивание и др.

В настоящей работе рассматривается вопрос физико-математического моделирования и численного анализа собственно совместно протекающих процессов осаждения кристаллов сахарозы на фильтрующей поверхности ротора и отвода межкристального раствора (мелассы) из рабочего объема машины типа ФЦНД.

Известно, что количественный анализ процесса разделения суспензий с помощью машины данного типа затруднен тем, что этот процесс развивается в рабочем объеме оборудования, имеющего сложную цилиндроконическую форму, в условиях значительной плотности обрабатываемой жидкостной системы, вариативности частиц твердой фазы по размеру и др.

Поэтому в работах [1–8], посвященных исследованию процесса разделения суспензий в ФЦНД, кинетики накопления, промывания и обезвоживания слоя осадка кристаллов, с целью преодолеть трудности расчетного характера, авторы работ исходили из ряда допущений, упрощающих постановку и решение данной комплексной задачи. Однако при этом оказались не учтенными такие особенности процесса как дисперсность взвеси, фактор стесненности осаждения твердых частиц в жидкости, кинетика накопления осадка и др.

Применительно к количественному анализу близкой по содержанию рассматриваемой здесь проблемы, а именно, задаче об обработке утфеля I кристаллизации [6], следует отметить, что в данной работе предложен более обоснованный по сравнению с ранее известными аналогами количественный анализ процесса разделения суспензии в рабочем объеме фильтрующей центрифуги периодического действия. Причем в предложенной с учетом особенностей анализируемого явления в работе [6] предлагается методика расчета процесса на базе средств современных информационных технологий. Используя данную методику, разработчик инновационного продукта получает возможность производить необходимое корректное прогнозирование процесса на базе режимных параметров проектируемого оборудования.

В то же время, имея в виду большое число, часто варьируемых в заметном интервале определяющих протекание процесса центробежного разделения суспензии в ФЦНД физикомеханических, геометрических и режимных параметров, для практических целей желательно располагать выражениями параметров управления данным процессом на основе безразмерных и критериальных величин. Что позволяет снизить количество этих параметров, и, кроме того, адаптировать результаты лабораторных исследований на натурные образцы центробежного оборудования.

Изучая процесс седиментации в гетерогенной системе “жидкость +твердое” в роторе центрифуги с непрерывной выгрузкой осадка, используют допущения о том, что данная система содержит зернистую агрегативно устойчивую взвесь из частиц небольшим размером δ сферической формы, частицы в процессе осаждения не слипаются и не сцепляются друг с другом, не изменяют свою форму и размеры. Дополнительно предполагают, что плотность ρ т твердого выше плотности ρ ж жидкости, а суспензия, с заданным гранулометрическим составом твердой фазы и объемным содержанием твердого с , предварительно равномерно перемешана. Что, в целом, не сильно искажает рассматриваемое реально протекающее явление.

Исходя из принятых положений, количественный анализ процесса центрифугирования суспензии в роторе ФЦНД осуществляют по трем этапам.

На первом этапе проводят обоснование геометрических параметров цилиндра, моделирующего коническую часть ротора центрифуги.

Второй этап расчета отводится анализу кинетики пробной частицы твердой фазы заданным размером в потоке жидкости в рабочем объеме центрифуги.

На третьем этапе исследования, на базе найденного выражения текущего критического диаметра частицы, заданной дисперсности твердой фазы в исходной субстанции и интегративного показателя эффективности процесса разделения суспензии, на конкретном примере, проводится численный расчет исследуемого процесса с содержательным анализом результатов расчета по критериальным параметрам.

Первый этап исследования

С гидродинамической точки зрения разделение суспензии в роторе ФЦНД представляет собой кинетический процесс обработки в центробежном силовом поле двух различающихся по плотности взаимодействующих и взаимопроникающих сред в канале, ограниченном сопрягающимися стенками цилиндра и конуса.

Поскольку процесс разделения суспензии реализуется в основном на ситовой поверхности конической части ротора ФЦНД, то сначала проводят обоснование приближенной геометрической модели канала для данного участка ротора. Для чего, учитывая, что формализация и количественное моделирование собственно процесса разделения жидкостной системы в общем виде затруднено, при постановке и решении данной задачи ее упрощают, используя специфические особенности исследуемого явления.

Так, течение жидкости в роторе фильтрующей центрифуги с рабочим объемом цилиндроконической формы и с полууглом конусности α порядка 30° принимают за осесимметричный тонкослойный поток (в реальных условиях отношение средней толщины hср слоя жидкости h к его длине Lпо порядку величин -^-®1%), а характер течения жидкости – как ламинарный и безнапорный (рисунок 1).

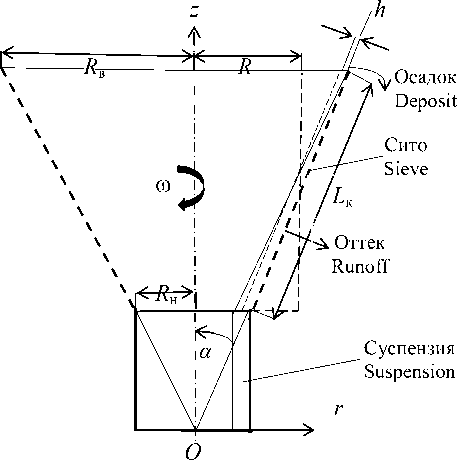
Рисунок 1. Схема к расчету геометрических параметров ротора центрифуги

Figure 1. The scheme to calculation of geometrical parameters of a rotor of the centrifuge

Тогда, если Rн и Rв – соответственно, радиус нижнего и верхнего сечения конической части ротора, то в качестве радиуса R цилиндра, моделирующего данную часть ротора, приближенно принимают полусреднее значение из величин нижнего и верхнего сечений конической части ротора, т. е. полагают

R = ( R h + R e )/2 ,            (1)

а в качестве радиуса r0 свободной поверхности потока ro = R - h ,                (2)

где R – вычисляют по (1), h – средняя толщина потока.

В допущении, что суспензия перемещается по ситовой поверхности в поршневом режиме, среднее значение скорости v z = w 0 потока в осевом направлении определяют по формуле

Q

^ 0     /п2    2 ч ^,

^{п (} R ^- r o )

где Q – производительность (расход)центрифуги по суспензии, R и h заданы по (1) и (2).

В свою очередь, если пренебречь влиянием осадка на фильтрующую способность центрифуги, то скорость по радиусу u = u r фильтрации жидкости через ситовую поверхность ротора рассчитывают согласно закону Дарси [3]

u = k^ pro² R , ^µ

где k 0 – коэффициент проницаемости ситовой поверхности, µ –динамическая вязкость жидкости, ρ – плотность жидкой фазы суспензии.

В таком случае, если полагать, что в роторе центрифуги жидкая фаза суспензии полностью фильтруется через ситовую поверхность, то расчетное значение эффективной длины составит

L = Q /(2 Ru) ,             (5)

где u вычисляют по (4).

Второй этап исследования

Учитывая, что в процессе седиментации твердой фазы действующие в суспензии на твердую частицу силовые факторы ориентированы в основном по радиусу, а частица перемещается по оси z как взвешенная с расходной скоростью w 0 = u z , согласно принципу Даламбера, в связанной с ротором системе координат r и z (рисуно к 2) в проекциях по осям r и z условия равновесия приложенных к частице сил приближенно записывают в виде уравнений кинетики частицы [7]

k52r - (vr - ur) = 0,(6)

vz - uz = 0,(7)

где k = ro2A /(18^),(8)

ω – угловая скорость ротора, рад/с; Δ = ρ 1 – ρ > 0, ρ и ρ 1 – соответственно, плотность жидкой и твердой фаз суспензии, кг/м³; µ – динамическая вязкость жидкости, Па ⋅ с; δ – диаметр частицы, м;

r – текущий радиус частицы, м; u r , v r – соответственно, переносная скорость жидкости и скорость частицы, по радиусу м/с; u z , v z – скорость жидкости и скорость частицы по оси ротора, м/с.

Поскольку решением системы уравнений (6), (7) является vr = u + kS2 r , vz = w0           (9)

где u =ur, k – определяют по (8), то исходя из дифференциального уравнения траектории частицы dr / dz = vr / vz, с учетом (9), приходят к дифференциальному уравнению dr     dz krS2 + u  w0

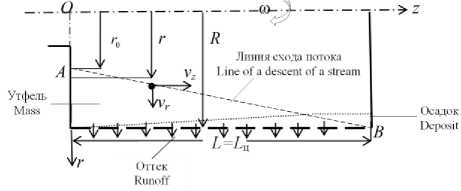
Рисунок 2. Схема к расчету процесса осаждения твердой фазы в роторе центрифуги

Figure 2. The scheme to calculation of process of sedimentation of a firm phase in a centrifuge rotor

При этом на базе (10), выражающее связь между параметрами потока жидкости и крупностью разделения (текущим критическим диаметром δ ) для перемещающейся по траектории АВ (где А ( r, 0), В ( R, L ))гипотетической частицы, характеристическое уравнение имеет вид

R

dr kS2 r + u

L = ∫ dz .

В силу того, что разделению жидкостных систем в роторах машин типа ФГШ обычно подвергают сгущенные суспензии, скорость седиментации частиц по радиусу корректируют множителем [6]

U = и (c ) = (1 - c )³<1 ,         (12)

где с – объемная концентрация твердой фазы в суспензии.

В результате чего вместо уравнения (11) используют уточненное соотношение

Rdr

* kUS² r + u

L = ∫ dz , 0

интегрируя которое получают характеристическое уравнение, куда входит параметр δ –собственное значение (текущий критический диаметр) краевой двухточечной задачи для частицы, перемещающейся по траектории АВ (рисунок 2)

kUS² R + u_x  kUS² L

F(S, r) = ln(—— ----)-- kUS r + u     w0

= 0. (13)

Полагая в (13) r =r 0 , приходят к характеристическому уравнению для δ = δ кр – глобальному (наибольшему по величине) расчетному значению критического диаметра.

Учитывая, что уравнение (13) включает параметр δ неявным образом, данный параметр находят расчетным способом с помощью оператора

S ( r ) = F ~4 r , to , c , ц , S ) ,         (14)

обратного заданному по (13) оператору F .

Третий этап исследования

На базе (14) определяют относительную массу η оседающего твердого (коэффициент осветления, %), составляющую [3]

η =

m ^ ^t¹ = "^ j Ф [ S ( r )] rdr ,   (15)

m 0       ^r1      r 0 r₀

-

где m 0 , m 1 – соответственно, масса частиц в исходной суспензии и в осадке, Ф(δ) – массовая характеристическая функция распределения частиц такая, что

Ф ( S ) = т ( 5 > ^ >, m 0

m – масса частиц размером δ >δ ^′ , m 0 – масса частиц в исходной суспензии, δ′ – зависящий от параметров управления критический диаметр вычисляют по (13).

Численный эксперимент

В соответствии с предложенной на базе (14), (15) расчетной схемой и технических параметров промышленной центрифуги ФВИ-1001К-1 [5] осуществляли количественный анализ эффективности процесса центробежного разделения суспензии, выбирая в качестве пробной модели жидкостной системы утфель III кристаллизации.

Параметры центрифуги ФВИ-1001К-1: производительность машины по осадку Q m = 8 т/ч; R н = 0,167 м, R в = 0,5 м – соответственно, радиус нижнего и верхнего сечения конической части ротора; R = 0,333 м приведенный радиус цилиндра, L =L ц = 0,652 м – длина ротора, h – 5 мм – средняя по длине ротора толщина потока суспензии, r 0 = 0,328 м – радиус свободной поверхности потока; угловая скорость ротора ω = 183 рад/с.

Физико-механические параметры утфеля (ориентировочно): с = 0,3…0,5 – объемная концентрация кристаллов сахарозы в утфеле; p i =1560, р = 1450 кг/м³ - соответственно, плотность сахарозы и межкристального раствора; ц = 2 Па - с - динамическая вязкость межкристального раствора; к о = 2 х 10^-10 м² - коэффициент проницаемости ситовой поверхности [3, 8].

Предполагали, что массовая характеристическая функция распределения твердой фазы по крупности определяется зависимостью

1 при 0 <  5 <  5 ,

Ф ( 5 ) = j ( 5 - 5 ) / ( 5, - 5 ) при 5 < 5 < 5 , (16)

0 при 5 > 5, где 81 = 10 "4 м, 82 = 10 -3 м, соответственно, минимальный и максимальный диаметр частицы твердой фазы (сахарозы).

Учитывая разнообразие физико-механических и геометрических параметров, определяющих протекание процесса центробежного разделения суспензии в ФЦНД, целесообразно располагать выражениями параметров управления данным процессом в безразмерной форме, с использованием критериальных величин. Для чего в качестве характерных величин процесса выбирали R , го и р - соответственно, радиус цилиндра, угловая скорость ротора и плотность межкристального раствора, что позволяет сократить количество переменных задачи на три – по числу характерных величин.

В результате чего, в рамках критериального моделирования, расчетная формула (14) выражается через критериальные комплексы: Та = («R2 / v)2 -число Тейлора (первое) - удельное значение центробежной силы по отношению к вязкостной силе, v =ц/р - кинематическая вязкость жидкости, и число Рейнольдса Re = w0R/v - удельное значение силы инерции в осевом направлении к силам вязкости. А также симплексные величины: § = L / R - удельное значение длины цилиндра к его радиусу; X = р / р - отношение плотностей сахарозы и межкристального раствора (эффективная плотность); к = к0 /R2 - удельное значение коэффициента к0 проницаемости ситовой поверхности в долях площади сечения цилиндра.

Поэтому вместо формулы (13) получают характеристическое уравнение

Ф ( r , Ta , Re, c , Я , § , X , 5 ) = ln( ⁵ 2 + ^Я ) -

5 ( r / R ) + Я (17)

_ UTa ( X — 1) 5² ₌₀

18Re где X = 18к /[U-(x- 1)], 5 =8/R - безразмерный диаметр частицы, выраженный в долях R – радиуса цилиндра, U = U(c) - вычисляется по (12).

При этом в соответствии с (17) коэффициент осветления п составляет

m(t)200

П = —1— = —5---7 Ф[R5(r)]rdr ,(18)

m 0    rl - r0 r где

5 = ф-( r, Ta, c, Я, §, X)

оператор, обратный (17), черточки над безразмерным диаметром 8 по умолчанию опущены.

Формулы (7), (11), (14), (16), (18), (19) являются базовыми при количественном моделировании процесса разделения суспензии в роторе ФЦНД.

При выбранных значениях режимных параметров центрифуги ФВИ-1001К-1 получили следующие величины: на основе формулы (3) значение расходной скорости потока составило w ₀ = 0,214 м/с, период Т = L / w ₀ пребывания пробной частицы в роторе Т = 3,05 с (что близко к наблюдаемому значению периода Т в реальных условиях [5]), а также значения безразмерных параметров Та = 2,18 х 10 8 ; Re = 51,67; § = 1,96; X = 1,08; к = 1,8 х 10^-9; X = 1,98 х 10^-6. Поэтому при числовых расчетах числу Тэйлора придавали значения Та = 2,1 х 10 8 ; 2,3 х 10 8 , а число Рейнольдса варьировали в области значений Re = 50–100 (рисунки 3, 4).

Результаты расчетов на базе приведенных параметров и решения уравнения (15) по глобальному критическому диаметру частиц показаны в виде графиков рисунка 3.

Визуальный анализ кривых данного рисунка выявляет согласующуюся с физическим смыслом задачи зависимость глобального критического диаметра 8 кр частиц от режимных параметров процесса центрифугирования (при фиксированных значениях остальных параметров): возрастание 8 кр (что соответствует ухудшению условий разделения суспензии) вместе с увеличением концентрации с твердой фазы и параметра управления – числа Рейнольдса (т. е. когда расход суспензии растет), и убывание 8 кр в том случае, когда число Та Тейлора растет, что свидетельствует об улучшении условий разделения суспензии (рисунок 3, кривые 1,3 и 2,4).

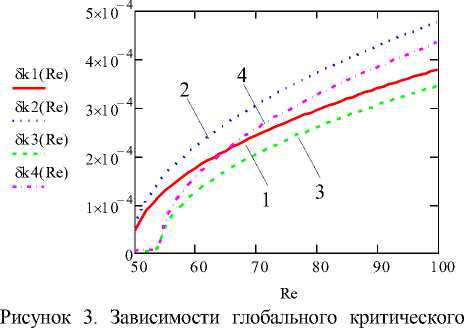
диаметра частицы 5 к (м) от числа Рейнольдса при различных значениях числа Тейлора и объемной концентрации с кристаллов сахарозы (Та =2,1 х 10 8 :1 -с = 0,3,2 - с = 0,4; Та =2,3 х 10 8 :3 - с = 0,3,4 - с = 0,4)

Figure 3. Dependences of global critical diameter of a particle 5 _к (m) on Reynolds's number at various values of number of Taylor and volume concentration с of crystals of sucrose (Та =2,1 х 10 8 : 1 - с = 0,3, 2 - с = 0,4; Та =2,3 х 10 8 : 3 - с = 0,3, 4 - с = 0,4)

В свою очередь, для принятого в форме (17) распределения твердого в жидкости визуализация данных рисунок 4 также подтверждает соответствие рассчитанных данных физическому смыслу процесса центрифугирования. А именно, отмечается убывание коэффициента осветления п , когда концентрация с увеличивается, т. е. выявляется снижение эффективности процесса разделения суспензии при большей сгущенности взвеси в суспензии (соответственно, кривые 1 и 2; 3 и 4, рисунок 4) и параметра управления – числа Рейнольдса (все кривые рисунка 4) .

В свою очередь, как и должно быть, коэффициент п возрастает, (т. е., острота разделения суспензии повышается), когда число Та Тейлора растет (а, значит, увеличивается и движущая сила процесса), что свидетельствует об улучшении условий разделения суспензии (соответственно, кривые 1 и 3; 2 и 4 того же рисунка).

Для режимных значений параметров машины Та =2,18 х 10 8 ; Re = 51,67; с = 0,4 расчет