Критериальное управление территориальным распределением кадровых ресурсов противопожарной службы Вьетнама

S. 2–3. URL: (data obrashcheniya: 27.04.2019).

В работах [11] территория Вьетнама (провинции и города республиканского подчинения) в результате решения задачи типологизации на основе кластерного анализа распределились по пяти однородным, компактно расположенным в географическом смысле группам по состоянию пожарных рисков.

Синтез территорий Вьетнама в однородные группы дал возможность эффективно решать задачи, связанные с совершенствованием управления ресурсами противопожарных служб, улучшением нормативно-правового обеспечения и организации их взаимодействия.

В частности, в работах [12; 14] показано, что решение задачи оптимального территориального распределения кадровых ресурсов противопожарной службы по кластерам связано с количественным исследованием зависимостей удельных показателей деятельности подразделений пожарной безопасности. Исходя из поведения частных удельных показателей, сформирован комплексный удельный показатель s , учитывающий как погибших, так и травмированных на пожарах [14].

А именно в аддитивном виде представлены показатели удельной нагрузки по числу погибших на пожарах, приходящихся на одного пожарного (УНПП), – d_i и удельной нагрузки по числу травмированных на пожарах, приходящихся на одного пожарного (УНТП), – w_i , взвешенные нормированными коэффициентами:

s i = a d i + в w i ,                                       (1)

где i = 1, 2,..., I - номера точек наблюдения (годы);

I – общее число лет наблюдения;

• α – вес удельного показателя d_i ;

• β – вес удельного показателя w_i .

На сумму весовых коэффициентов налагалось ограничение a + в = 1.                                     (2)

После нахождения весовых коэффициентов α, β и параметров наилучшая модель для Вьетнама записывается в виде [14]

s k = (0,555 d k + 0,445 w k ) = 0,0025 exp (7 h k ) ; k = 1, ..., K ,                (3)

где h_k – количество пожаров, приходящихся на одного пожарного в k - м кластере;

K – общее число территориальных кластеров, различающихся пожарной обстановкой.

При этом значение коэффициента объясняемости эмпирических данных моделью равно 96,3%. На рисунке 1 приведены эмпирические данные и теоретическое описание связи комплексного удельного показателя s от УНП ( h – удельная нагрузка по пожарам – число пожаров, приходящихся на одного пожарного во Вьетнаме, за период 2008–2017 гг., экспоненциальная модель).

96 в ыпуск 2/2019

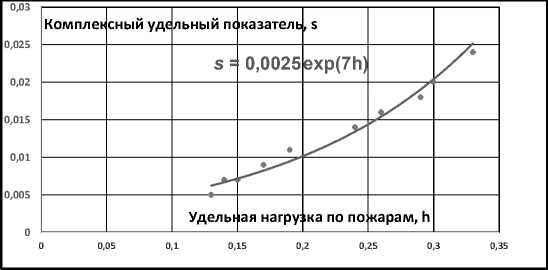
Рис. 1. Эмпирические данные (ромбы) и теоретическое описание связи комплексного удельного показателя s от УНП во Вьетнаме (экспоненциальная модель)

Опираясь на результаты работы [13], построим математическую модель типа «затраты – результаты» для более эффективного территориального распределения кадровых ресурсов противопожарной службы.

Применительно к k - му кластеру Вьетнама запишем в общем виде целевую функцию:

^ф k = ^ф k ( F k , R k , ^Yk ) ,                                 (4)

где F_k – число пожаров в k - м территориальном кластере;

R_k – количество пожарных в k - м кластере;

Y k - вектор параметров целевой функции в к - м кластере.

Примем, как и в [13], что целевая функция (4) монотонно увеличивается в области 0 <  R_k < ∞. То есть чем выше обеспеченность противопожарной службы в кластере кадровыми ресурсами, тем больше целевая функция, причем она асимптотически ограничена сверху:

Ф k ⁽ Fk , ” , Y k ) = Ak = const.                          (5)

Целевая функция общей системы противопожарной службы Вьетнама Ф_ц определяется целевыми функциями ее подразделений в кластерах. Определим целевую функцию Центра Ф_ц в виде их суммы:

Ф ц = 1 ф k ;k = 1, -, K ,                     (6)

k = 1

Будем называть критериальным управлением управление кадровой системой противопожарной службы в кластерах путем выбора целевых функций, отражающих распределение ее кадровых ресурсов. Принцип, реализованный в данной постановке задачи распределения Центром (в данном случаем – главным органом управления) кадровых ресурсов противопожарной службы по кластерам, является принципом оптимального распределения.

Центр, располагая ограниченными ресурсами, стремится достичь оптимального значения своей системной цели (общей целевой функции), определяя целевые функции активных элементов (противопожарных служб в кластерах) [14] путем выбора такого распределения кадровых ресурсов, который стимулирует их к совершенствованию форм

Минаев В.А., Топольский Н.Г., Кйеу Т.А. Критериальное управление...    97

и методов оперативно-служебной деятельности при тушении пожаров, интенсификации использования наличных ресурсов.

Территориальное распределение кадровых ресурсов при известной зависимости ф k ( F k ,R k , Y) и известных параметрах Y k ставится как следующая задача оптимизации:

k = K            __

Фц = Е^k (Fk,Rk, Yk) ^ oPtim k=1

при ограничении на количество кадровых ресурсов, которыми располагает Центр:

k = K

ERk = R.

k = 1

Для формирования целевой функции используем обратную величину зависимости (3), отражающей связь удельной нагрузки по пожарам c комплексным удельным показателем по взвешенному числу погибших и травмированных на пожарах:

1 / s_k = 400exp (–7 h_k ) .                             (9)

Примем за целевую функцию для подразделений k -го кластера

Ф k = 400 [1-exp (-7 hk )],                         (10)

которая имеет следующий графический вид (рис. 2).

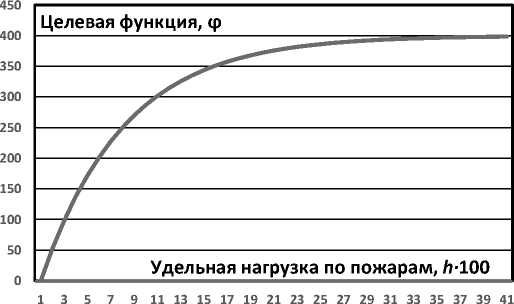
Рис. 2. Целевая функция по комплексному удельному показателю числа погибших и травмированных на пожарах в зависимости от удельной нагрузки по пожарам

Нетрудно заметить, что функция φ _k всегда больше нуля, монотонно увеличивается, с ростом R_k стремясь к величине 400 . Очевидно, что распределение кадровых ресурсов по кластерам должно быть таким, чтобы обеспечивать с точки зрения Центра интегральный оптимум суммы целевых функций (7), отражающих комплексные удельные показатели о взвешенных числах погибших и травмированных на пожарах.

Учитывая малость h k ,, с целью получения аналитических зависимостей для оптимального распределения кадровых ресурсов по кластерам упростим выражение (10), разложив экспоненту в ряд Маклорена.

98 в ыпуск 2/2019

Тогда

фk - 400 [1 -1+7hk --2!hk2 + -hk -...], или

Ф k = 400 h k ( 7 - 25 h k + 57 h_k ²-_ ) ; k = 1, 2, ..., K .

Целевая функция Центра в этом случае представляется в виде k = K

Ф ц ■ 400 Z h k ( 7 - 25 h k + 57 h k ) .

k = i

Таким образом, задача оптимального распределения Центром кадровых ресурсов противопожарной службы Вьетнама между K кластерами ставится в виде

Ф → min, цR k=K

Z Rk = R.

k = 1

Решим задачу (14)–(15) методом множителей Лагранжа.

Функция Лагранжа записывается в виде k=K

k = K

L ( Ф ц ) = 400 E ^hk ( 7 - 25 h k + 57 h 2 HI E ^Rk — H

k = 1

k = 1

где λ – множитель Лагранжа.

Условный экстремум выражения (16) находится из соотношений d L (R, X ) = d L (R, X )

^{d R}k

dX

= 0; k = 1, 2, .„, K .

Подставим в (16) выражение h k = F k / R k :

k=K F (      F      F 2 ^   (k=K^

L (ф ) = 400V - L 7 — 25 - k - + 57 -X R R , - R .

\  ц/           pl        p       P 2

k=1 Rk V       Rk      Rk )    V k=1

Вычисляя из (17) производную —-—,—- = 0, получим приведенное уравнение чет-∂Rk вертой степени относительно Rk и используем его для реализации метода Феррари:

Rk 4 + pRk2 + qRk + r = 0, где p = 28-102 F-; q = -2-104 F-; r = 684-102 -^. X            X

Необходимо отметить, что четвертая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в общем виде. И в этом аспекте настоящая статья, в которой находится решение уравнения (19), развивает результаты, полученные в работах [13; 14] для более простых случаев.

Для применения указанного метода уравнения четвертой степени на первом этапе приводятся к уравнениям, у которых отсутствует член с третьей степенью. Именно таковым является (19).

Минаев В.А., Топольский Н.Г., Кйеу Т.А. Критериальное управление...    99

На втором этапе с учетом нулевого коэффициента при члене третьей степени в (19) решается дополнительное кубическое уравнение резольвенты:

z ³ - pz ² - 4 rz + 4 pr - q ² = 0.

Подставляя в уравнение (20) значения коэффициентов из (19), получим или

z—

28 · 10 ² F 2 k z

λ

—

2736 ·10 ² F ³

---------- z +

λ

76608 · 10 ⁴ F_k ⁴    4 · 10 ⁸ F_k ⁴

λ ²

—

λ ²

= 0,

3    28·10 ² F k 2

zz λ

Введем обозначения:

—

2736·10 ² F ³     3,6608 ·10 ⁸ F ⁴

---------  z + —-----^ ---— = 0.

λ               λ ²

28 ·10 ² F

a =---; b = -

λ

2736 ·10 ² F_k ³

λ

;

c =

3,6608 ·10 ⁸ F_k ⁴

λ ²

.

Представим уравнение (21) в каноническом виде: x ³ + a 1 x + b 1 = 0,

a где z = x--= x +

28 · 10 ² F           b          10 ¹⁰ F ⁶

------ ; a_A ^ c —² = - 2,5 —;

3λ ¹        3            λ ²

2 b ³ bc

b =---+ c =

¹    27    3

108 F4 (

-°-^ 3,66 +

X ² I ,

3,34 < F ³ 1,52 4 0 7 F, ⁵ ) 1,52 •10 ¹⁵ F ⁹ kk  k

—

λ

λ

λ ³

.

10 ¹⁰ F k ⁶               10 ¹⁵ F k ⁹

и ит ак, a        ,             ;           ,

, 1               λ 2        1                 λ 3

.

Вычислим дискриминант кубического уравнения (24), используя известную формулу:

3           2        30    18

Q = [ al 1 +| bl 1 = 21A- I

I 3 J I 2 J X6

I ■ 0.

Введем обозначения, используемые в формулах Кардано:

или

A = B = -3b72 = 0,25 -°—k-

^{N 1}                X

.

Поскольку дискриминант (25) равен нулю, из формул Кардано следует, что уравнение (24) имеет при любом λ >  0 следующие действительные корни:

• один положительный :

z = A + B = 2 A = 0,5 -°— L. ; 0 ,

• два кратных отрицательных:

A + B . A — B

^Z12 =

—

10 ⁵ F_k ³

X

.

100 в ыпуск 2/2019

Используя (27), найдем корни исходного уравнения четвертой степени (19), применяя известные формулы метода Феррари:

—

—

Г a 4| v + zо

—

b l )

^Rk 1,2 =

—

Г a1 41 ~ + z 0 +

Ь1   l

^Rk 3,4

Нетрудно показать, что единственный положительный корень равен

R

k ₃

2 z 0 - 41 ^1 + z 0 +

b i )

или после соответствующих подстановок и преобразований

В итоге получаем

_{R 4} 30 10 ⁴ _F 7/4 k 3        λ 2 k .

7/4

R.₍   . = R--- A -----.

^k ( opt 3 )             K 7/414

L k = 1 F k

Результаты моделирования

Сравним эффективность территориального распределения кадровых ресурсов противопожарной службы Вьетнама, используя работы [13; 15], в которых получены линейные и квадратичные аналитические приближения для R_k .

Так, в работе [13] при учете только линейного члена в разложении в ряд Маклорена

получено соотношение

F

^R k ( opt 1 ) = ^R^K^A₁

В работе [15] при разложении в ряд Маклорена учтены члены до квадратичного и по-

лучено соотношение

^Rk ( opt 2 )

= R

³ F k ²

^K 3   2

^ k = 1\ F k

.

В настоящей статье учтен кубический член в разложении в ряд Маклорена:

R

^k ( opt 3 )

= R

F_k 7/4

^K 7/4 .

^ k = 1 F k

Минаев В.А., Топольский Н.Г., Кйеу Т.А. Критериальное управление...

Пропорциональное распределение кадровых ресурсов, к которому обычно прибегают в практике территориального распределения ресурсов, имеет вид

Rk  ^ = R k (проп)

F k

X LFk

.

Сравним различные варианты распределения кадровых ресурсов по выделенным кластерам при различных приближениях модели (рис. 3).

Из анализа рисунка 3 можно сделать следующие практические выводы:

• 1.    Линейное (34), квадратичное (35) и пропорциональное (37) приближения модели не позволяют с уверенностью говорить о том, что найденные на их основе решения по территориальному перераспределению кадровых ресурсов противопожарной службы достаточно устойчивы, в то же время они свидетельствуют о явно сформировавшихся направлениях указанных процессов.

  

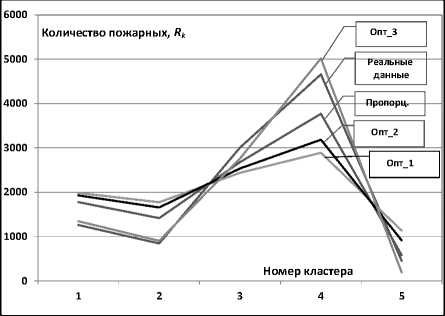
  Рис. 3. Сравнение распределений кадровых ресурсов при различных приближениях модели

  
  

• 2.    Кубическое приближение модели (36), подтверждая выявленные направления перераспределения кадровых ресурсов, свидетельствует о необходимости и возможности плавного и планомерного управления данными процессами, а именно: для повышения эффективности использования кадровых ресурсов противопожарной службы страны необходимо дополнительно усиливать кадровый состав ее подразделений в 1-м (на 6,8%), 2-м (на 7,2%) и 4-м (на 7,7%) кластерах за счет их планомерного снижения в 3-м (на 8,1%) и 5-м (на 58,2%) кластерах (нужно отметить, что предполагаемые изменения в 5-м кластере, существенно отличающиеся от других территориальных единиц, связаны с незначительной обеспеченностью кадровыми ресурсами противопожарной службы – всего 4,4% от ресурсов Вьетнама).

Выводы

• 1.    Задача оптимального распределения ресурсов противопожарной службы должна решаться на основе комплексных критериев, отражающих влияние деятельности противопожарной службы на ущерб от пожаров.

• 2.    Построение критерия оптимального распределения кадровых ресурсов связано с исследованием зависимости комплексного аддитивного показателя, отражающего взвешенное количество погибших и травмированных на пожарах от нагрузки – количества пожаров, приходящихся на одного пожарного в кластере.

• 3.    Целевую функцию противопожарной службы целесообразно строить исходя из принципов создания математических моделей типа «затраты – результаты», представляющих собой сумму целевых функций этих же служб в однородных по пожарным рискам территориях – кластерах.

• 4.    Для практических расчетов территориальных распределений кадровых ресурсов аналитическими службами противопожарной службы необходимо учитывать члены третьего порядка малости в разложении целевой функции в ряд Маклорена.

• 5.    Во избежание резких и неприемлемых скачков для управления кадровыми ресурсами противопожарной службы при общем ограничении на них без снижения эффективности их использования необходимо планомерно перераспределять названные ресурсы в процессе ежегодных перерасчетов.

• 6.    Развитие рассмотренной в статье модели видится в направлении комплексного учета ресурсов противопожарной службы, включающих не только кадровые, но и материально-технические, технологические, финансовые и иные ресурсы.

102 в ыпуск 2/2019