Критерии моделирования

Целью моделирования является построение теории, которая могла бы объяснить наблюдаемое поведение системы. На ее основе могут быть найдены оптимальные параметры системы и область их изменения, проведена имитация действий системы для оценки результативности, выбора вариантов и технико-экономического прогнозирования. При моделировании системы необходимо в упрощенной форме отобразить существенные черты, позволяющие проводить эксперименты по исследованию параметров системы [1].

Наряду с этим функциями модели могут быть: осмысление действительности, средства общения, обучения и прогнозирования.

Процесс построения модели состоит из следующих этапов:

• •    постановка задачи, построение критерия;

• •    определение взаимосвязи параметров;

• •    выбор параметров, подлежащих исследованию.

• •    модель может быть выбрана из числа существующих подходящих моделей или создана специально, искусственно;

• •    исследование модели в отношении свойств, закономерностей и параметров, представляющих интерес;

• •    проверка работоспособности модели.

При построении критерия модели рекомендуется применять следующие общесистемные принципы:

Принцип включения, предусматривает учет требования со стороны более сложной подсистемы.

Принцип системного единства или системности состоит в том, что целостность системы должна отображаться критерием.

Принцип развития предусматривает возможность наращивание и совершенствование.

Принцип комплексности заключается в том, что в критерии должен обеспечивать связное отображение элементов системы в единое целое.

Принцип совместимости состоит в том, что показатели, используемые при построении критерия, должны быть согласованы по времени и размерности.

Принцип вариантности предусматривает возможность замены одной формы представления другой.

Принцип однозначности состоит в том, что единственное значение критерия модели соответствует каждому состоянию системы.

Принцип адекватности предусматривает соответствие результатов моделирования результатам наблюдения реальной системы.

Принцип эффективности позволяет использовать в критерии моделирования показатели, дающие значительное его изменение.

Вид математического критерия может выражать абсолютную или относительную величину зависимого показателя. Критерий может быть составным, комплексным или интегральным. Построенные комплексные показатели могут содержать показатели различной природы: как интегральные, так и итоговые, и стоимостные части. Критерий может быть аналитическим, функциональным или быть представлен в виде уравнения. Система показателей, описывающая моделируемую систему, должна содержать наименьшее их число при наибольшем их влиянии.

Каждый показатель системы должен проверяться на однородность [2]. Если показатель однороден, то для него при необходимости можно построить закон распределения случайной величины и определить вероятность её появления. Используя метод главных компонент на корреляционной матрице показателей системы, показатели системы должны быть упорядочены по степени влияния или разброса показателей [3]. Для уменьшения числа показателей, входящих в критерий, необходимо пересчитывать корреляционную матрицу. Определение вида включения производится на основе уравнения распределения по методике, описанной в статье [4].

Выбор числа показателей, эффективно описывающих моделируемую систему, производится по схемам, приведенным в статье [5]. Оценивание эффективности использования критерия для математической модели производится по методике, описанной в [7]. В начале исследования определяются значимости коэффициента корреляции для показателей, полученных при моделировании, и реальных данных системы.

Затем определяется значимость уравнения критерия, полученного с помощью регрессионного анализа [8]. Если при различных наборах значений независимых показателей в реальной системе наблюдаются одинаковые значения зависимых показателей, то критерий оценивается на адекватность [9]. Оценка остатков уравнений и их корректировка описана в монографии [10] и применена в статье [11] при моделировании факторов управления урожайностью риса.

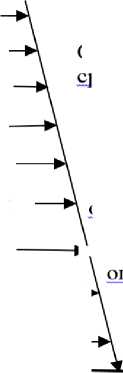
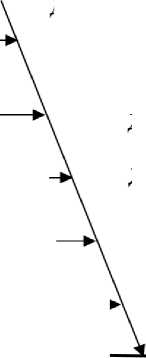
На основе вышеописанного была построена причинно-следственная диаграмма (диаграмма Исикавы) критерия модели [12], приведённая на рис. 1.

Принципы

Системности

Развития

Однозначности

Включения

Вариантности

Эффективности

Адекватности

Совместимости

Комплексности

Средство

Средство

'авнения

Средство оценки параметров

Функции

Цели применения

Для оценки результативности—►

►\ Инструмент

Средство оценки эксперимента

Для выбора вариантов

Для оптимизации

Для технико экономического прогнозирования

Для исследования параметров и ограничений

Критерий модели

Абсолютный—►

Аналитическое —►

Относительный

Составной —►

В виде уравнения

Однородность—►

Распределение —»

Упорядочение —»

Комплексный

Функциональное *■

Выбор числа

Интегральный —>

Пр ед ст а вле н не

Выбор включения *

Значимость связи

Значимость модели—^

Адекватность —ь

Оценка остатков —>

Корректирование

Вид критерия                    Показатель       Оценивание

Рисунок 1 - Причинно-следственная диаграмма критерия модели

В диаграмме описываются цели, функции, принципы построения и оценки критерия модели. В критерии эффективности, по которому ведется сравнение состояний производства в разные моменты времени, (стоимость продукции, затраты труда, затраты на материалы, затраты основного капитала) являются абсолютными показателями, представлены в денежных единицах [13]. Эффективность производства - относительным показателем. Но в общем случае произвольная система может оцениваться не с помощью критерия денежного эквивалента, а с применением другой системы единиц. Например, в образовании эффект процесса обучения оценивается баллами.

В работе [14] критерий, выраженный аддитивным выражением, оценивает эффективность внесения в почву мелиорантов, повышающих урожайность выращиваемых культур. Критерием сравнения выступает составной показатель, полученный как латентный показатель методом главных компонент.

В работе [15] приведена методика упорядочения показателей сельскохозяйственного производства по степени влияния и процедура построения комплексного критерия для определения эффективности системы. В указаниях [16] рассматриваются разноплановые показатели, характеризующие эффективность хозяйственного водопользования, которые объединяются в критерии сравнения.

Построение критериев, содержащих факторы управления сельскохозяйственным процессом, на основе нахождения функций плотности распределения факторов управления и объединение их в мультипликативный критерий проведены в статье [17].

В общем случае критерий статистического моделирования ( K) выглядит следующим образом:

K = С f(x 1 ) f(x ₂) ... f n ( X n ), (1) где x i - i -й показатель, описывающий рассматриваемую систему;

n – число независимых показателей системы;

f_i ( x_i ) – плотность распределения показателя x_i ;

С – свободный коэффициент.

Плотность распределения независимого показателя моделируемой системы может иметь следующий вид:

fi(xi) = exp(ai xi2 + bi xi), где exp – экспоненциальная функция;

a i и b i – искомые коэффициенты параболического уравнения.

Параметры С , a i и b i критерия (1) определяются методами корреляционного анализа [10]. Найденные параметры однозначно описывают систему в определенном состоянии Х = ( x 1 , x 2 , …, x n ). Задавая приращения последовательно каждому показателю из множества Х , можно определить оптимальную стратегию управления для повышения эффективность рассматриваемой системой.