Критерии устойчивости линейных систем и математические модели их анализа

Устойчивость систем в области изображений с учетом Лапласа эквивалентна стабильности систем во временной области. Для изучения устойчивости систем мы используем такой пробный сигнал, как входная функция (входной сигнал). Различают три типа устойчивости:

• -    статическая устойчивость;

• -    динамическая устойчивость;

• -    частотная устойчивость.

Критерий устойчивости.

Рассмотрим стационарную линейную систему, передаточная функция которой, с учетом преобразования Лапласа, равна

k(s - z 1 )(s - z 2 )…(s - z m ) (s-p 1 )(s-p 2 )…(s-p n )

где z j (j=1, 2, ...m) – нули системы;

p i (i=1, 2, ... n) – полюса и k=b m /a n . С учетом преобразования Фурье

k(jω-z 1 )(jω-z 2 )…(jω-z m )

G(jω) = (jω-p1)(jω-p2)…(jω-pn)

Y(jω) = G(jω)X(jω)(3)

ω = 2πf(4)

Статическая стабильность . Чтобы изучить статическую устойчивость, сигнал Дирака должен подаваться как входной

сигнал на систему, которая изначально должна находиться в состоянии покоя. В этом случае имеем

Y(s) = G(s)X(s) =

k(s -z₁)(s-z₂)…(s-z_m) (s-p 1 )(s-p 2 )…(s-p n )

Поскольку для сигнала Дирака X(s)=1

k(s - z 1 )(s - z 2 )…(s - z m ) (s - p 1 )(s -p 2 )…(s-p n )

Используя алгебраическую факторизацию, имеем

A 1      A 2          A n

Y(s) =     +     + ⋯ + s-p1  s-p2     s-pn переходя из области изображений во временную область с помощью обратного преобразования Лапласа, имеем

y(t) = A 1 e^p1t + A 2 ^∗e^p2t + ⋯ + A n e^pnt

Каждое слагаемое Aiepit (i=1, 2, ... n) может иметь различную эволюцию в зависимости от того, являются элементы действительными или комплексными. Если значения действительные, то они могут

быть положительными, нулевыми или отрицательными, и три возможных варианта развития событий представлены на рисунке 1.

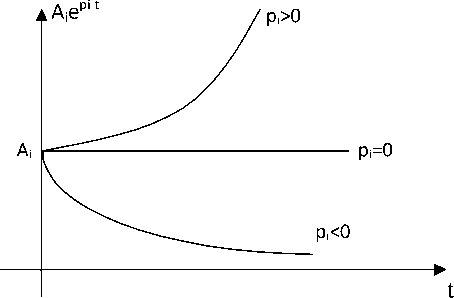
Рис. 1. Эволюция термы Aiepit, в области вещественных значений

Если полюсные элементы комплексные, то, конечно, существует также сопряженный полюс pi*, потому что комплексные алгебраические корни всегда находятся в паре. В этом случае мы имеем pi = αi + jωi pi∗ = αi - jωi используя формулы Эйлера

y(t) = Aiepit + Ai∗epit = 2Aeαitcosωit(11)

где A i = A i * = A.

В зависимости от того, является ли действительная часть α i положительной, отрицательной или нулевой, пара комплексных

полюсов может иметь три возможных варианта развития, представленных на рисунке 2.

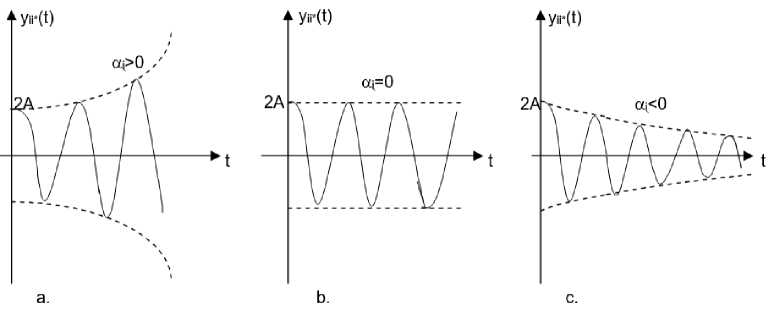
Рис. 2. Эволюция терма y ii* (t) с учетом одной пары комплексных полюсов a)    действительная часть α i положительна, b) действительная часть α i равна нулю, c)

действительная часть α i отрицательна

В соответствии с данным определением статической устойчивости можно сказать, что система обладает статической устойчивостью только в том случае, если полюса системы являются отрицательными действительными или имеют отрицательную действительную часть, если полюс является комплексным.

В любом случае, граница стабильности – это мягкая форма нестабильности. Также отметим, что критерий статической устойчивости эквивалентен общему критерию устойчивости.

Динамическая устойчивость . Применим однократный ступенчатый сигнал на входе к системе, которая, как предполагается, изначально находится в состоянии покоя. Поскольку X(s)=1/s, входной сигнал добавляет нулевой действительный полюс к выходному сигналу Y(s)=G(s)X(s).

Согласно данному определению динамической устойчивости, справедливо следующее: система обладает динамической устойчивостью только в том случае, если полюса системы являются отрицательными действительными или имеют отрицательную действительную часть, если полюс является сложным.

Частотная устойчивость . Что касается (2) и (3), то мы видим, что если входной сигнал синусоидальный, то амплитуда постоянного отклика выходного сигнала бесконечна и не ограничена, если m>n или в передаточной функции есть воображаемый полюс.

На самом деле, если m>n, то мы имеем нестабильность для очень высокой частоты (ω→∞)

lim G(jω) = ∞                               (12)

ω→∞

Если передаточная функция имеет один воображаемый полюс p i =jω i , то член jω i -p i =0

lim G(jω) = ∞ ω→ω_i

В этом случае система нестабильна по частоте, потому что она нестабильна для частоты ω=ω i .

Система обладает стабильностью по частоте только в том случае, если m≤n и в передаточной функции нет воображаемых полюсов.