Критерий для выбора геометрической модели абразивного зерна

В производстве абразивного инструмента для резания, шлифования, полирования и точной обработки изделий из металлов, сплавов и минералов используются порошки природных и чаще синтетических алмазов. В целях сравнения производительности инструментов из натуральных и искусственных алмазов были проведены обширные лабораторные и промышленные испытания. Сравнивались расход энергии, чистота поверхности и износ кругов из натуральных и синтетических алмазов. По внешнему виду партия натуральных алмазов кажется темно-серой или черной массой. При рассмотрении каждого алмазного зерна в отдельности можно видеть, что искусственные алмазы, также как и природные, могут иметь различные оттенки от белого до черного. При сравнении искусственных алмазов с природными можно отметить большое сходство и существенные различия между ними. Поразительным является правильность кристаллической формы алмазов, выращенных синтетически. Искусственные алмазы имеют легко различимую правильную форму. Среди природных алмазов правильные кристаллы с совершенно четко очерченными гранями встречаются редко; чаще встречается округлые кристаллы или кристаллы неправильной формы. Это объясняется тем, что в природных условиях алмазы растут, когда они ограничены окружающими породами и приобретают форму, соответствующую контурам окружных пород. Круглые кристаллы могут образоваться в результате шлифовки или растворения после того, как алмаз вырос. При синтезе алмазов, когда кристаллизация идет у тонкой пленки металлического катализатора при достаточном количестве графита, получается равномерное распределение графита по всей поверхности кристалла.

Режущая способность шлифовальных инструментов, эффективность их применения, а также качество обработанных поверхностей во многом зависят от линейных размеров зерен.

При моделировании процессов шлифования важным является использование формы абразивных зерен в качестве базовой модели. В научной литературе имеются различные взгляды на выбор таких моделей. В работе [1] наиболее вероятной представляется форма зерна в виде конуса с закругленной вершиной, а также шара, в работах [2, 3] – в виде эллипсоида вращения. Авторы исследования [4] описывают профиль зерна кривыми второго порядка. В работе [5] рассматривается форма алмазного зерна в виде цилиндра и куба. С учетом этих различий нами проведены сравнение различных моделей и регламентация их по степени приближения к экспериментальным данным.

Цель работы: анализ адекватности выбора базовой модели абразивных зерен, используемых в алмазных инструментах.

Мы исходим из предположений, что абразивные зерна – совокупность частиц произвольной формы и различной дисперсности, распределенные в объеме материала статистически равномерно со случайной пространственной ориентацией. Микрочастицы системы могут быть выпуклыми телами любой геометрической формы, одинаковой для всех микрочастиц системы. Частицы различаются только размерами. Находящееся на плоскости зерно в ряде случаев располагается так, что размеры, видимые в плане и принимаемые за длину и ширину, меньше третьего размера, условно называемого высотой и видимого на второй проекции [6, 7]. Следовательно, для выбора геометрической модели формы реального алмазного зерна необходимо наиболее точно определить линейные размеры зерна по объемным измерениям в двух проекциях. В качестве геометрической модели зерна абразивного наполнителя выбирался такой вариант модели, при котором параметр D , характеризующий величину отклонения объема реального зерна V r от объема его модельного аналога V m , принимает минимальное значение:

P

D = |1 - [ Е ( V mi /V ri Я^ P I (1) i = 1

где i, P – порядковый номер и количество исследованных зерен, соответственно. Совокупность линейных измерений, необходимых для вычисления V r и V m , определяется формой АЗ.

Необходимые для моделирования процедуры контрольного ситового рассева размерные характеристики зерен определялись по двум проекциям, полученным с помощью растрового электронного микроскопа РЭМ XL-20 (Philips) в режиме вторичных электронов. Линейные размеры оценивали по трем взаимно перпендикулярным направлениям. За длину зерна принимался его наибольший размер, видимый на одной из двух проекций (рис. 1). Измерение длины и ширины проекции зерен, их высоты по РЭМ-фотографиям. Примеры диаграмм распределения коэффициента формы зерна по размерным интервалам их значений приведены на рис. 2.

Как известно, коэффициент формы Кф отдельного зерна определяется как отношение длины его проекции к ее ширине. Изометрич-ность зерен (в процентах), следуя методике стандарта [8], определяли по формуле u = u1 -100, (2) n где u1 – число изометричных зерен, n – число измеренных зерен. Число изометричных зерен u1 считали по результатам вычисления коэффициента формы. Число изометричных зерен u1 считали по результатам вычисления коэффициента формы. Изо-метричным считают зерно, коэффициент формы Кф которого не превышает 1,3. Полученные таким образом значения изометричности зерен исследовавшихся порошков показаны в таблице 1.

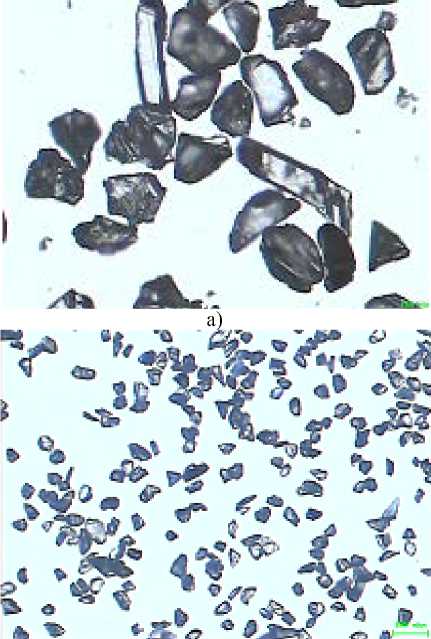
б)

Рис. 1. Зерна шлифпорошков из природных алмазов (а ) – зернистости 125/100;

(б) – зернистости 50/40

Таблица 1. Анализ адекватности выбора базовой модели алмазных зерен

Исследуемые шлифпорошки существенно различаются по коэффициенту формы (рис. 2). Распределение этой характеристики в случае порошков синтетического алмаза имеет меньший вариационный размах значений и более высокую частотность, а модальное ее значение соответствует интервалу 1,2÷1,3. Для порошков природного алмаза наблюдается полностью обратная картина: вариационный размах значений более широкий, частотность меньше, а модальное значение лежит в области значений коэффициента формы больше 1,3. Следствием этого является существенное различие изометричности зерен. У шлифпорош-ков синтетического алмаза она значительно выше, чем у шлифпорошков природного алмаза (табл. 1). Данное обстоятельство дает основание говорить о том, что шлифпорошки синтетического алмаза содержат большее количество зерен правильной (округлой) формы. Улучшение изо-метричности зерен, как известно, может быть достигнуто применением процедуры сортировки порошка по форме зерен на вибростолах [9].

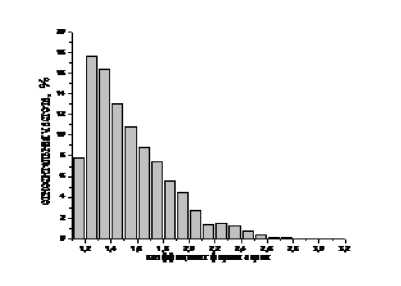
а)

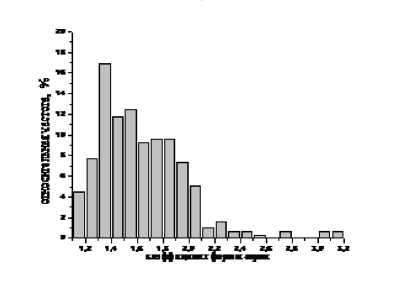
б)

Рис. 2. Гистограммы распределения коэффициента формы зерен шлифпорошков синтетического (а) и природного (б) алмаза зернистостью 50/40

На рис. 1 приведены РЭМ-фотографии зерен исследованных алмазных шлифпорошков. Видно, что зерна природных алмазов являются совокупностью осколочных частиц неправильной формы, произвольное сечение которых в подавляющем большинстве случаев можно считать четырех- или пятиугольниками, как и в других несферических порошках. При визуальном рассмотрении зерен шлифпорошков алмаза установлено, что зерна шлифпорошка из синтетических алмазов имеют округлую форму, а зерна из природных алмазов имеют в основном пластинчатую и игольчатую формы, встречаются кристаллы с четкой огранкой и с острыми ребрами.

Выводы: всего было изучено по 250-300 зерен каждой разновидности исследованных алмазных шлифпорошков. Для выбора геометрической модели формы реального алмазного зерна необходимо наиболее точно определить линейные размеры зерна по объемным измерениям в двух проекциях. Правильный выбор базовой модели абразивных зерен содействует оптимизации процессов шлифования.