Критерий компактности в пространстве комплексных борелевских мер

Сначала вводим некоторые обозначения ^’{О}. с^НЧЧЧЧ.

^•НЧЧЧ-ДМ

–это линейное пространство непрерывных финитных функций на . В пространстве вводится понятие сходимости. Последовательность функций f n ^е Ф сходится к функ-ции f в пространстве ^, если f n - равномерно финитны и последовательность ^fn равномерно сходится к ^f на ^{R 0} . То есть существует компакт B ⁽ 0 ^,r 1М0 ^,r 2 ) ^{,r 1 >} r ² такой, что supp f n ° B ⁽ 0 ^,r 1И 0 ^,r 2 ) и последовательность ^{f n} равномерно сходится к ^f на .

Напомним теперь некоторые определения и результаты из теории интеграла и меры.

определена вещественная борелевская мера μ ,       – борелевское множество. Ограничением(сужением) меры μ на множество E называется мера μE , которая определяется формулой                для любого борелевского множества .

Если ^е = ^Р , то говорим, что мера ^р сосредоточена на множестве E .

Носителем меры ^μ (обозначение supp ^μ ) называется наименьшее замкнутое множество, на котором сосредоточена мера.

Меры μ1 и μ2 называются взаимно сингулярным, если они сосредоточены на непересекающихся борелевских множествах E1 и E2 .

Сформулируем следующие известные теоремы,

Теорема Жордана. Всякая вещественная мера однозначно представляется в виде ^Р = ^Р + ^{— Р} - , где ^Р + и ^Р - - взаимно сингулярные положительные меры.

Мера ^Р + называется положительной составляющей меры ^р .

Мера ^{Р -} называется отрицательной составляющей меры ^р .

Теорема Хана. Для любой вещественной меры ^μ в области ^G существует разложение ^G на два непересекающихся множества ^{G 1} и ^{G 2} , причем

• ^р ( E ) - 0 при ^Е ° G 1

• ^{р (} E ) - ° при ^Е ° G 2

Хотя разложение "        не единственно, но меры р + ир- определяемые формулами                 ,                не зависят от выбора G1 и G2.

Из этих теорем следует, что если ^μ – вещественная борелевская мера на , то существует борелевские множества ^{E 1} и ^{E 2} такие, что

• 1)             ,

• 2)            ,

• 3) V + = Р е 1 ,р - = Р е 2 .

Величина ^{1 р |} = ^{р +}+ ^р - называется полной вариацией или модулем меры Р

Вещественная борелевская мера ^μ на называется локально конечной, если для любого компакт ■ ^_ ■ выполняется неравенство I ^р 1 ( K ⁾ .

Комплексной борелевской мерой называется функция множеств р (Е), представляемая в виде р (Е) р 1( Е)+ip 2 (E), где р 1, р2

–

конечные

вещественные борелевские меры.

Обозначим через семейство функций множеств , представимых в виде р р 1 р2, гдер 1, р2 вещественные локально конечные борелевские . функция μ определена на борелевских множествах за исключением тех Е , для которых                . В частности функция μ будет определена и счётно аддитивна на всех борелевских множествах с ри компактным в замыканием.

Две меры        называются эквивалентными, если выполняется равенство             для любых борелевских множеств Е , указанного выше вида.

Теорема 1. CM [5] Всякий элемент “ - ' эквивалентен разности ^{р 1 р} 2 , где где ^{μ 1} и ^{μ 2} – положительные взаимно сингулярные локально конечные борелевские меры на . Причем ^{μ 1} и ^{μ 2} определяются однозначно.

Теорема 2.  CM[6] Всякая широко ограниченное множество в ^с является сильно огранич-енным множеством.

Теорема 3 (критерий компактности в ^с). Для того, чтобы множество было компактным, необходимо и достаточно, чтобы оно было широко ограниченным.

Доказательство. Необходимость. Докажем от противного. Пусть H с^с— компактное множество. Допустим, что оно не является широко ограниченным. Тогда существует функция          и последовательность рт е Hтакие, что выполняется неравенство |(рт’^)|“m. Но у последовательности μm есть сходящаяся подпоследовательность. Получили противоречие. Необходимость доказана.

Достаточность. Пусть Hc^с - широко ограниченное множество. По теореме 2 оно является сильным ограниченным. Это означает, что для

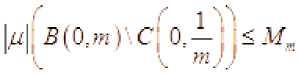
любого m— 2 существует конст-анта Mm такая, что для любой меры р е H. Пусть “ произвольная последовательность мер из -“ . По теореме Алаоглу у последовательности есть подпоследовательность

( 0.2 ) i ( o , 2 )

B

Из

которая слабо сходится к некоторой мере ν2 на компакте метода математической индукции следует, что существует

последовательность “ , k—2,3. •••. такая, что последовательность “ является

подпоследовательностью

последовательности

V;

и

последовательность слабо сходится к некоторой мере ^{ν k} на

B ( 0 ,к ) б ( 0 , 1 )

^k . Можно считать, что каждая мера ^νk есть мера на ,

компакте

считая ^νk

B равной нулю вне компакта

( 0 ,к ) * ( 0 , 2)

^k . Тогда берём диагональную

последовательность ^ak ^ k , которая будет слабо сходиться к мере ^vm

на

B

компакте

B

компакте функция,

( ⁰ .m Ц⁰ .m ) ( ⁰ ,m u( ⁰ .m )

для любого m — ² .

совпадают. Берём

что и в тексте доказательства

ф е С ( B ( 0 ,m +1 ) l ( 0 .— +1 ) ) ф е С ( B ( 0 ,т +2 ) б ( 0 ,

Докажем, что ^v m ⁺ 1 и ^v m ⁺ 2

функцию ψ , которая та

на

же

предыдущей теоремы. Тогда

))

. Поэтому

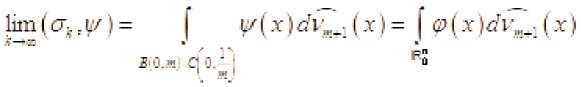
lim( ст.,L/) = ( ^( х) аЧ „_. (х)

.

Далее, как и в доказательстве предыдущей теоремы, получаем совпадение

B ( 0 ,т Ш0 . -)

^m . Строим

ограничений мер ^v m ^{+ 1} и ^v m ^{+ 2} на компакте

B ^{( 0} .m Ц⁰ .m )

последовательность vm как ограничение меры vk+1 на компакте и меру Vе^ с такую, что для любого m—2

ограничение ^μ на компакте

B ( 0 ,m Wg , -)

^m есть ^νm .

Теперь докажем, что последовательность σ k сходится к μ . Пусть ϕ – произвольная функция из

. Существует такое ⁿ , что

ф с B ( 0 ,m ) i(0 , 1| с B ( 0 ,т +1 ) i| 0 , — supp               ^{m                 m + 1}

Поскольку последовательность ° k слабо сходится к ^v k ^{+ 1} на компакте

B ( 0 ,т ⁺ 1 Ы0 ,      )      lim ( _а к ,ф ) = ( + 1 ,ф ) = ( ^,ф ) = ( _р,ф )

^{т + 1} , то т ^-< ^х '             . Теорема доказана.

Говорят, что сеть радоновых мер μr ,       , широко сходится к мере ν при

, если для любой функции

(реФ^)

выполняется равенство

lim ( Р г ^,ф ) = ( ^v,ф ) r ->х

Теорема 4. Пусть μr ,        – сеть радоновых мер и пусть для любой функции ф существует предел (^г’ф) при _ . Тогда сеть Vrшироко сходится к некоторой мере ν при .

Доказательство.

Пусть последовательность tm> 0 сходится к бесконечности. Из условия теоремы следует, что последовательность μtmшироко ограничена. По теореме

3 у последователь-ности tm есть подпоследовательность τ m такая, что последовательность μτm широко сход-ится к некоторой радоновой мере τ Докажем, что Vr— v при _ ?:. Если это не так, то существуют число £ 0>0, последовательность rm— ^ и функция ' такие , что '(^Гт’ф) ^’ф^ £°. Это неравенство противоречит соотношениям (^Тт’ф)-(v,ф) и (^Тт ^гт,ф) — 0. Теорема доказана.

Теорема 5. Если последовательность комплексных радоновых мер является сходящейся, то у неё существует подпоследовательность , такая что послед-овательности , , будут сходящимися

Доказательство. Из того, что последовательность сходится, следует, что она является широко ограниченной. По теореме 3.2 она будет сильно ограниченной. Значит сильно ограниченными будут последовательности

,      ,       . Тогда по теор-еме 3.8 эти последовательности будут компактными. Из этого легко следует утверждение теоремы. Теорема доказана.

Пусть ^μ – радонова мера, ^E – борелевское множество. Множество ^E называется измеримым по Жордану относительно меры ^μ , если I № Е ) = 0 . Из теоремы ^{0 . 5} [5] вытекает следующее утверждение.