Критерий плавления Линдемана и переход стекло - жидкость

Природе размягчения стекла – процесса, обратного стеклованию жидкости, посвящено довольно много работ. Тем не менее данная задача не решена до конца [1-4]. В сообщении рассмотрено условие перехода стекло – жидкость, основанное на концепции, заложенной в критерии плавления Линдемана. Согласно этому критерию, при температуре плавления кристалла T_f среднеквадратичная амплитуда тепловых колебаний атомов достигает некоторой критической величины <Δr m² > ^1/2 , составляющей определенную постоянную долю δ L характерного межатомного расстояния r C у различных кристаллов

( (Ar 2

m

S L =   ~ const ,

• I        r2I

• V         C 7 t = t f

где δ L – параметр Линдемана, значение которого колеблется в небольших пределах у разных кристаллов

σL ≈ const ≈ 0.15 -0.20(2)

Постоянство δ L выполняется лучше у кристаллов одного класса.

Поскольку в стеклах ближний порядок примерно такой же, как и в соответствующих кристаллах, естественно предположить, что нечто подобное критерию Линдемана должно иметь место и в случае стеклообразных твердых тел. Будем полагать, что как при температуре плавления кристалла [6, 7], так и при температуре размягчения стекла [8, 9] происходит делокализация группы возбужденных атомов решетки, приводящая к ее неустойчивости [7]. Под делокализацией атома в стеклах подразумевается его критическое смещение из равновесного положения Δrm, соответствующее перегибу кривой потенциала U(r) (рис. 1) [10]. В качестве кинетической единицы, подвергающейся делокализации, выступает мостиковый атом типа атома кислорода в мостике Si-O-Si у силикатных стекол [10, 11], ответственный за переключение валентной мостиковой связи ― элементарного акта процесса вязкого течения стеклообразующих расплавов и стекол [12].

В приближении модели гармонического осциллятора при температуре размягчения T = T g энергия теплового движения возбужденного атома (1/2)kT g становится равной работе его критического смещения Δr m , которая запасается в виде потенциальной энергии предельной упругой деформации межатомной связи (1/2)a< Δr m >,

2 a <^A r„ 2) = 2 kT ₆ ,                                                (3)

где k – постоянная Больцмана, a – коэффициент упругости (коэффициент жесткости связи). Отсюда квадрат среднеквадратичного смещения возбужденного атома выражается формулой kT

{A r m ²) =       .                                                     (4)

a

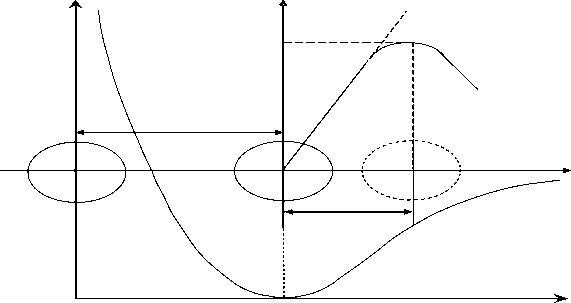
Рис. 1. Схема делокализации атома. Δrm – критическое смещение (делокализация) атома, соответствующее перегибу кривой потенциала U(r), иначе, максимуму силы межатомного взаимодействия Fm

Если принять во внимание связь a с модулем упругости при одноосной деформации E = a/r o , равенство (4) запи-

сывается в виде (r o – среднее межатомное расстояние)

< A r m ²) = kT ^ .

Er ₀

В модели делокализованных атомов аморфных веществ [10] вводится элементарный флуктуационный объем Δν e = πd ² Δr m , необходимый для делокализации атома,

^A V e

3 ( 1 - 2 Ц ) kT ₈

fE J g

где μ – коэффициент Пуассона, f g = (ΔV e /V) T=Tg – доля флуктуационного объема системы, замороженная при температуре стеклования, ΔV_e = N_eΔν_e, N_e – число делокализованных атомов.

Разделив обе части равенства (5) на r o² и подставив в него kT g /E из соотношения (6), приходим к следующей формуле

T - T g

3 ( 1

f

\f ^A v

² A H r 0 ³

.

Объем делокализации атома Δν e должен быть близок к атомному объему ν ~ r o³ (ν = V/N), ибо его можно рассматривать как «объем флуктуационной дырки» ν h , куда смещается возбужденный атом [11]. Можно показать [13], что Δν e составляет около 80% от r o³

Δν e ≈ 0.8 r 0³ .

Равенство (7) с учетом (8) принимает вид

f g

( 1 - 2 A ) J ^.

По аналогии с параметром плавления Линдемана δL введем «параметр размягчения» δ

(^A О ) ^1/2 ~ f ^0.27 L ) r 02 ^J 1 ( 1 - 2 A ) J

Сравнение с экспериментом и обсуждение результатов

Величина fg в соотношении (10) определяется по экспериментальном данным об «универсальной» постоянной C1 уравнения Вильямса – Ландела – Ферри, описывающего температурную зависимость вязкости (времени релаксации) в области стеклования [10], f » — » const » 0.020 - 0.030. (11) g C1

Коэффициент Пуассона меняется в узких пределах, у стекол одного класса μ ~ const. Поэтому следует ожидать, что параметр стеклования (10) будет фактически универсальным у различных стекол. В самом деле, как видно из табл. 1-3, у ряда неорганических стекол он в первом приближении оказывается универсальной константой f (A r )1/2

5 - I 2^ I « const ® 0.11 - 0.14 (12) ( ^r 0 J

Постоянство δ лучше выполняется у стекол одного структурного типа. Например, у калиево-боратных стекол имеем δ =0.14 (табл. 1), а у сульфатно-фосфатных стекол – δ =0.10 (табл. 2). У щелочно-силикатных стекол наблюдается слабый рост δ с увеличением размеров ионов щелочных металлов: δ ~ 0.13-0.14 (табл. 3).

Таблица 1

Калиево-боратные стекла

Стекло	μ	fg	δ	Δr m /r o
K O-B O 3 K O, mol. % 1.1	0.292	0.034	0.15	0.10
2.5	0.293	0.033	0.14	0.10
3.9	0.293	0.032	0.14	0.10
8.5	0.293	0.030	0.14	0.10
13.0	0.295	0.030	0.14	0.10
18.0	0.301	0.029	0.14	0.09
22.8	0.295	0.028	0.14	0.10
28.2	0.288	0.027	0.14	0.10
33.5	0.303	0.026	0.14	0.09

Необходимые экспериментальные данные взяты из справочника [14] и других источников [10, 11].

Соотношение (12) – это полуэмпирический критерий элементарного акта процесса размягчения стекол, который по аналогии с правилом Линдемана можно сформулировать следующим образом: когда среднеквадратичная амплитуда тепловых колебаний атома <Δrm2>1/ достигает определенный доли среднего межатомного расстояния ro (около 10-15% от ro), атом возбуждается, теряет устойчивость и начинается переход стекло– жидкость. С этой точки зрения размягчение стекла обусловлено, так же как и в случае плавления кристаллов, возникновением колебательной нестабильности атомов в узлах решетки. По-видимому, элементарные акты переходов кристалл–жидкость и стекло–жидкость в первом приближении имеют общую природу. Критическое смещение атома из равновесного положения сопровождается перегруппировкой соседних частиц и носит энтропийный характер [8].

В связи с изложенным выше представляет интерес формула для относительного критического смещения атома из равновесного положения, следующая из динамики решетки [4, c. 24;15, c. 206], что находится в согласии с результатами расчета γ D по известному уравнению Грюнайзена [16, 17].

^A r m =    ¹

rо 6Yd ’ где параметр Грюнайзена γD, характеризующий ангармонизм колебаний решетки, можно рассчитать по данным о коэффициенте Пуассона μ [16]

Таблица 2

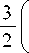
1 + Ц ) 2 - 3 ц J ,

Сульфатно-фосфатные стекла

Стекло	μ	f g	δ	Δr m /r o
NaPO 3	0.294	0.016	0.10	0.10
NaPO 3 -Na 2 SO 4 Na2SO4, mol. % 10	0.299	0.016	0.11	0.09
20	0.292	0.016	0.10	0.10
30	0.288	0.015	0.10	0.10
NaPO 3 -K 2 SO 4 K 2 SO 4 , mol. % 10	0.316	0.013	0.10	0.09
20	0.316	0.014	0.10	0.09
30	0.313	0.014	0.10	0.09
0.4NaPO 3 ∙0.6Na 2 SO 4	0.320	0.011	0.09	0.10

Y d

Легко убедиться, что у рассмотренных выше стекол отношение критического смещения атома Δr m к среднему межатомному расстоянию r o , так же как и параметры δ L и δ, является приблизительно универсальной константой (табл. 1-3),

A r                   _,

—— ® cons t ® 0 .09 - 0.11,                                    (15)

r ₀

по порядку величины, близкой к параметру Линдемана (2), и параметру стеклования (12).

Таблица 3

Щелочно-силикатные стекла

Стекло	μ	f g	δ	Δr m /r o
Na 2 O-SiO 2 Na 2 O, mol. % 19.6	0.234	0.029	0.12	0.12
29.45	0.254	0.028	0.13	0.11
30.1	0.255	0.028	0.13	0.11
32.9	0.255	0.028	0.13	0.11
36.3	0.255	0.029	0.13	0.11
K2O-SiO2 K 2 O, mol. % 16.7	0.236	0.030	0.13	0.12
18.8	0.244	0.029	0.13	0.11
21.4	0.254	0.029	0.13	0.11
26.9	0.275	0.028	0.13	0.10
28.7	0.281	0.028	0.14	0.10
33.0	0.295	0.027	0.14	0.10

Заключение

При температуре размягчения отношение среднеквадратичной амплитуды тепловых колебаний атомов к среднему межатомному расстоянию является практически универсальной постоянной, которая по порядку ве- личины совпадает с параметром Линдемана. Предполагается, что переход стекло–жидкость обусловлен делокализацией возбужденных атомов, приводящей к колебательной нестабильности решетки.