Критерий стабильности для полупроводниковой сверхрешетки с омическим контактом

Хорошо известно, что полупроводниковая сверхрешетка с минизонным транспортным режимом теоретически может усиливать высокочастотное, в том числе ТГц электромагнитное излучение, в режиме отрицательной дифференциальной проводимости (ОДП) [1-2] в большом диапазоне частот. Однако, как было показано, в частности, в [3], в режиме ОДП волны зарядовой плотности оказываются неустойчивыми, что приводит к образованию как статических, так и движущихся доменов ганновского типа, препятствующих усилению. В связи с этим, усиление высокочастотного излучения в классической схеме усиления считается невозможным. Однако критерий устойчивости, развитый в [3] справедлив, строго говоря, только для сверхрешеток с бесконечным числом периодов и не учитывает реальные граничные условия. В данной работе мы показываем, что уже простое омическое граничное условие, наложенное на одну из границ сверхрешетки длиной L , изменяет критерий устойчивости, сдвигая область стабильности в область ОДП. Для анализа устойчивости системы в данном случае мы используем подход, развитый в теории эффекта Ганна [4] и основанный на анализе высокочастотного импеданса системы.

Вычислим импеданс полупроводниковой сверхрешетки, помещенной в стационарное электрическое поле напряженностью E , направленное вдоль оси сверхрешетки, в квазистатическом случае.

Плотность тока в сверхрешетке вдоль направления приложенного электрического поля будет иметь стандартный вид j = en0V0 ,                                           (1)

где e - заряд электрона, n₀

- концентрация носителей, V = V      01 cr^!

p 1 + ( E о, E ) 2

- дрейфовая

скорость электронов, V_p =Д d/2И , Д - ширина минизоны, d - период сверхрешетки,

Е_сг= И/ edz  - критическое поле, соответствующее максимуму статической ВАХ

сверхрешетки, т - время релаксации.

Рассмотрим произвольную флуктуацию внутреннего поля в сверхрешетке

E ( x , t ) = E _o + S E ( x, t ) , n ( x , t ) = n_Q + S n ( x , t )

В этом случае для анализа эволюции возмущения в системе необходимо уравнение (1) совместно с уравнением Пуассона и законом полного тока

дE  4~e t     \

=---- ^{( n - n} о ) .

дx £

решить

.tot    .    £ дE j = j 1 4п дt

где £ - диэлектрическая проницаемость. Заметим, что j^tot не зависит от координат.

С учетом (2) ток j вдоль оси сверхрешетки с точностью до членов первого порядка

малости будет иметь вид

J = ^en 0

д V V+— 0  дE

\

E = E о

S E + eV₀ S ,

)

д V где дE

V p ±-EErL

E = E о

E   [ 1 + ( E о, E ) ²Г

а уравнения (3) и (4) преобразуются к виду

дЗВ  4 ne e

----=---on , дx    £

to t

j = j +

£ дО 4п дt

Воспользуемся преобразованием Фурье по времени

«

Sf ( x , t ) = j f ( x , a )e ^a

-M

da

4 n ’

тогда для возмущения на частоте а получим, комбинируя (5), (6) и (7)

$ ^(a) =

e .

— а + en

[ 4 п      ⁰

д V д E

Ж ( x , a ) +

E = E о ;

eV д8Е(x,a)

4 п   д x

где  $ (а) - преобразование Фурье для электрического тока в сверхрешетке, включая ток смещения.

Решая уравнение (9) относительно SE (x, а), получим с учетом омического граничного условия SE (0,a) = 0 на левой границе сверхрешетки

Ж ( x , a ) = -^ $ ( a ) [ 1 - e - ^Sx / ^L ] ,                        (10)

eV0 S где

e_ 4nL S = eVо

e

— i a + en

^ 4 n       ⁰

d V д E

E = E о )

Вычислим импеданс сверхрешетки на частоте возмущения

Z (a) =

SJ (a) $(a) ’

где

L

S J ( a ) = j S E ( x , a ) dx - Фурье-образ потенциала вдоль оси сверхрешетки. Подставляя (10) в о

(12), получим

Z (a) =

4 nL² e- S + S - 1 eV o      S²

В режиме заданного напряжения нестабильность системы определяется нулями импеданса (или полюсами адмиттанса Y ( a ) = 1/ Z (a) ). Возникновение нулей импеданса означает нестабильность системы к возмущению на частоте a при заданном напряжении.

Введем пропорциональную дифференциальной подвижности электронов «дифференциальную частоту»

^a D

4 n sn₀ д V

e

д E

E = E о

«дифференциальный угол»

1 - F 2

0D = a, TL = a-------,                           (15)

D   DL     F (1 + F 2)

где T_L = L/V_o - «пролетное время» электрона, a = 4nen₀L/E_cr - безразмерный параметр, F = E₀/E_cr и «пролетный угол»

0 = a T = 0_O----- ,

L    0 _F

где 0_О = wL/V_p , Заметим, что классический критерий устойчивости, связанный с ОДП

предполагает возникновение нестабильностей при условии a_D <  0.

В этом случае выражение для S можно записать в удобном для анализа виде

S = ®_D + i © .

Как следует из (13), нули импеданса определяются нулями функции f ( S ) = e - ^S + S - 1.

Отделяя в (15) действительную и мнимую части и приравнивая их к нулю, получим

e © D cos 0 = 1 -0_D e ^-0 D sin 0 = 0

.

Решая систему (16) методом итераций, получим набор нулей S_n = (®_D)_n + i0_п

( n = 1,2,...), действительная и мнимая часть которых возрастает по модулю, начиная с n = 1.

Нестабильность возникает, когда хотя бы одна из частот а_п , соответствующих

данному S , будет иметь отрицательную мнимую часть. Следовательно, нестабильности

возникают, если уже мнимая часть а станет отрицательной, то есть Im ^ <  0.

Из (14) следует, что

а =

S — 0 D iT L

Следовательно, нестабильности возникают, если

10 d I <1 ( 0 D ) ,|.                                              (18)

Данный критерий согласуется с критерием устойчивости в теории ганновских нестабильностей, развитой в работе [4].

Решение уравнения (16) дает (0о)1^-2,09, следовательно, критерий (18) можно записать в виде

10 D | < 2,09 .

Заметим, что при этом выполняется и условие возникновения ОДП, то есть 0_Й <  0.

Перепишем критерий стабильности, используя (15), в виде так называемого критерия n0L, предложенного Крёмером [5] в теории эффекта Ганна n0L < 2,09 Ecr- F(1 + F1                          (20)

⁰         4 n e  1 - F ²

Видно, что критерий устойчивости критично зависит от длины сверхрешетки и концентрации электронов. Уменьшение длины сверхрешетки и концентрации носителей способствует стабилизации системы. На рис.1 изображена граница, разделяющая область стабильности (ниже сплошной линии) от области нестабильностей (выше сплошной линии). При больших концентрациях электронов (n0 > 1016 см-3) область нестабильности практически совпадает с ОДП. При более низких концентрациях электронов область стабильности может достаточно далеко зайти в область ОДП.

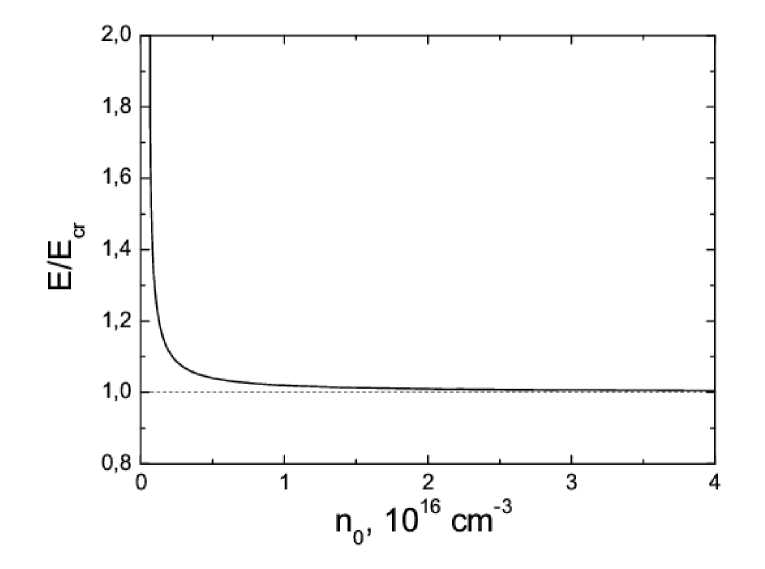
Рис.1. Зависимость области нестабильности согласно критерию (18) от концентрации электронов и напряженности постоянного электрического поля E . Выше сплошной линии находится область стабильности. Горизонтальная штриховая линия соответствует началу области ОДП.

Таким образом, в данной работе мы показали, что реальные граничные условия, наложенные на сверхрешетку, с учетом конечности ее длины могут дать критерий возникновения нестабильностей, отличный от критерия ОДП. В частности, наложение омического граничного условия дает критерий стабильности, сходный с критерием, известным в теории эффекта Ганна. В результате, область стабильности при не слишком высоких концентрациях электронов и не очень большой длине сверхрешетки, может сдвинуться в область ОДП, что может говорить о возможности экспериментального обнаружения эффекта усиления высокочастотного излучения в классической схеме усиления.