Критерий точности и анализ многоспутниковых систем непрерывного наблюдения земли

Многоспутниковые системы используются для наблюдения объектов с определением их координат на Земле и/или в приземном слое с применением оптических средств [1–3], радаров с синтезированной апертурой [4]. В качестве целей могут выступать неподвижные и/или движущиеся объекты (например, корабли или самолеты). В последнем случае необходимо выполнять серию наблюдений с их последующей обработкой с использованием сложных алгоритмов фильтрации [3, 5]. Выбор конфигурации таких спутниковых систем наблюдения (ССН) может быть выполнен на основе комплексного моделирования возможных вариантов. Наибольший интерес представляют сравнительные точностные характеристики. При таком моделировании необходимо учитывать геометрию ССН, характеристики и ограничения бортовой аппаратуры, а также особенности обработки результатов наблюдений (алгоритмы фильтрации, необходимость учета в ряде случаев высокоскоростной динамики объекта и т. п.).

Вместе с тем, для ССН, использующих результаты одновременного наблюдения с нескольких космических аппаратов (КА), можно построить математический критерий точности, который не связан с особенностями бортовой аппаратуры наблюдения. Данный критерий может использоваться для предварительного анализа конфигураций и отбраковки вариантов с заведомо худшими точностными характеристиками.

В статье представлен подобный критерий на основе расчета точности определения географических координат объектов и моделирования сравнительных точностных характеристик реализуемых ССН. Рассмотрено 18 вариантов возможных ССН на круговых орбитах с числом КА от 12 до 40. Представленные результаты могут использоваться для начального выбора структур оптимальных ССН.

Критерий точности наблюдения ССН

Для КА на высоте h , наблюдающего поверхность Земли, поле обзора представляет сферический сегмент на поверхности Земли с геоцентрическим углом Θ (рис. 1), зависящим от высоты орбиты и минимального угла возвышения α . Данные параметры связаны выводимым из теоремы синусов соотношением:

cos a

cos( 0 + a ) =

h

1 +

R

e где Re — экваториальный радиус Земли.

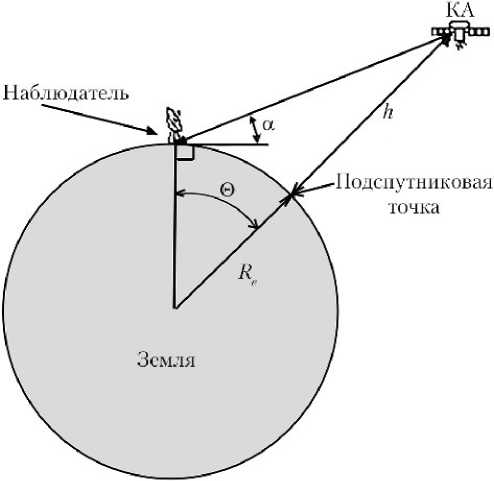
Рис. 1. Поле обзора космического аппарата (КА): R_e — экваториальный радиус Земли; h — высота КА; Θ — геоцентрический угол; α — минимальный угол возвышения

Сигналы, снимаемые с целевой аппаратуры, являются прямоугольными координатами Р _n и P _b, которые являются проекциями линии визирования на плоскость местного горизонта ( n O b ), т. е. вектор измерений:

P = k_P

cos ϕ cos γ

– c o s ϕ s i n γ

Без потери общности для сравнительных оценок можно принять, что k_p ≡ 1. Вектор измерений P связан некоторым нелинейным соотношением с неизвестными координатами объекта наблюдения:

P = f ( r _T).

Для одиночного наблюдения объекта с одного КА можно получить следующие соотношения:

Предполагается, что с КА проводятся угломерные измерения с использованием целевой аппаратуры (оптической, инфракрасной или радиотехнической). Геометрия обзора показана на рис. 2.

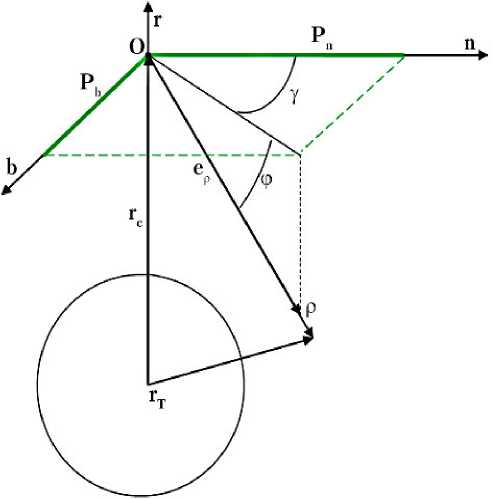
Рис. 2. Геометрия обзора: r _c — геоцентрический радиус-вектор КА; r _T — геоцентрический радиус-вектор объекта наблюдения; n , r , b — орты орбитальной системы координат КА; ρ — вектор линии визирования на объект; e _ρ — единичный вектор направления линии визирования; ϕ , γ — углы, определяющие положение линии визирования относительно орбитальной системы координат КА

P ^ρ

ρ

sin ϕ cos γ cos ϕ sin ϕ cos ϕ sin γ

∂p

∂ r _T

где

∂p

∂ ( ϕ , γ )

^{∂ ( ϕ , γ )} ∂ ρ

∂ ρ

= P P T = h , (1)

∂ r _T       ^{ϕγ ρ}

P ϕγ

sin ϕ cos γ –cos ϕ sin γ sin ϕ sin γ cos ϕ cos γ

матрица Р _ρ может быть получена дифференцированием выражения для вектора ρ :

ρ = ρ

cos ϕ cos γ sin ϕ cos ϕ sin γ

P = ρ ρ

cos ϕ

–sin ϕ cos γ sin γ cos ϕ

–sinϕsinγ cosγ

cos ϕ

T — матрица перехода от инерциальной геоцентрической экваториальной системы координат к орбитальной системе координат КА:

T =

r T r T      и x r T и x r T

--x---------------------" I ^r T I I ^r T I I U x r T II u x r _T l

Перемножение матриц P _ϕγ и P _ρ дает матрицу:

–sin² ϕ cos² γ + sin² γ      –sin γ cos γ (1 + sin² ϕ )

–sin γ cos γ (1 + sin² ϕ )     –sin² ϕ sin² γ + cos² γ

Это позволяет устранить вырожденность при ϕ = ± π /2 в матрице Р _ρ .

При наличии одновременных измерений с двух и более КА можно получить следующее линейное уравнение для ошибок измерений:

ΔΡ = ΗΔrT, где Н — матрица следующего вида:

H = [h1 h2 … hk], здесь hi — матрица вида (1) и k — количество одновременных измерений. Матрица Н имеет размерность 2×3k.

Квадрат ошибок измерений может быть представлен как

Δ r _T² = Δ r _T ^T Δ r _T = Δ p ^T ( H ^T H )^–1Δ p = Δ p ^T M ^–1Δ p .

Это выражение представляет собой квадратичную форму, а матрица М является положительно определенной. Поэтому можно повернуть систему координат, чтобы диагонализировать матрицу и преобразовать квадратичную форму к сумме квадратов. Таким образом, например, для среднеквадратических отклонений ошибок измерений и ошибок определения координат объекта наблюдения имеется соотношение:

о r С ^ trace [( M )^-1] о p = D о p .

В целом матрица М описывает геометрию ошибок измерений и не связана с особенностями целевой аппаратуры. Рассматривая изменение параметра D для различных моментов времени и положений цели, можно интегрально оценить сравнительные точностные характеристики измерений, реализуемых конкретными конфигурациями спутниковых систем.

Этот параметр имеет некоторую аналогию с широко используемым на практике интегральным критерием точности в ССН («Глонасс», GPS , Galileo ) — фактором потери точности ( dilution of precision ) [6]. Однако, последний критерий относится к измерениям псевдодальности.

Для спутниковых систем характеристики точности могут изменяться в широких пределах. В первую очередь это касается вертикальной составляющей ошибки. При малом угле между радиус-векторами КА эти ошибки могут доминировать, хотя для целей наблюдения больший интерес могут представлять горизонтальные ошибки, поскольку объект наблюдений находится на Земле или в приземном слое. Поэтому при моделировании ССН рассматривались горизонтальные составляющие ошибки определения координат объекта. В этом случае уравнение (1) примет вид:

∂ p

— = P P TS = h, где S — матрица перехода к топоцентри-ческой системе координат объекта наблюдения с выделением только горизонтальных координат:

S = MS(1:2 1:3)T, где         MS = [M1 M2 M3]T;

M ₃ = [cos ϕ cos λ cos ϕ sin λ sin ϕ ] ^T ;

M ₂ = [–sin ϕ cos λ –sin ϕ sin λ cos ϕ ] ^T ;

Mx M

M = ,         ^{3    2}-------- •

• ¹   ^ ( M ₃x M ₂) T ( M ₃x M ₂)

Численное моделирование ССН

В качестве возможных конфигураций ССН рассматривались известные спутниковые системы на круговых орбитах глобального непрерывного двух-, трехи четырехкратного обзора следующих типов:

• •    кинематически правильные спутниковые системы (КПС) [7, 8];

• •    околополярные спутниковые системы (ОПС) [9].

Все конфигурации систем являются однородными, т. е. все КА имеют одинаковые высоты и наклонения орбит.

Для оценки точностных характеристик ССН по каждой возможной конфигурации проводилось моделирование, учитывающее географическое положение объекта наблюдения. Отметим, что ССН на круговых орбитах практически не имеют в долговременном масштабе долготной неоднородности, и характеристики точности зависят, в основном, от широты объекта наблюдения.

Конкретные конфигурации ССН на круговых орбитах выбирались из каталогов [3, 4]. При этом, если для рассматриваемого числа КА N в каталоге имелось несколько возможных конфигураций, то в расчет бралась лучшая из них, определяемая по максимальному геоцентрическому углу Θ. Далее для каждой выбранной конфигурации ССН, построенной на определенной высоте, рассчитывалась горизонтальная ошибка. При этом последовательно рассматривались точки поверхности Земли на определенной заданной широте и долготе от 0 до 180° с шагом 1°. Для каждой рассматриваемой точки проводился прогноз положения ССН на период повторяемости. В сводную таблицу выбирался наихудший вариант, таким образом гарантируя непревышение указанного значения по точности при любых временных и долготных положениях наблюдателя.

Рассматривались ССН с общим числом КА N = 12–40; интервалом высот орбит h = 8 000–20 000 км; наклонениями орбит i , соответствующими источникам [7, 8], и географическими широтами объектов наблюдения ф = 0; 45; 75 ° .

Результаты моделирования показывают, что одними из основных проектнобаллистических параметров, определяющих точность ССН и существенно влияющих на стоимость их создания, являются два взаимосвязанных параметра: общее число КА N и высота орбиты h . В качестве примеров на рис. 3, 4 для конфигураций ССН двукратного обзора показаны цветные карты изолиний изменения погрешности наблюдений объекта на широте 45 ° в зависимости от количества КА N и высоты h для КПС (рис. 3) и ОПС (рис. 4).

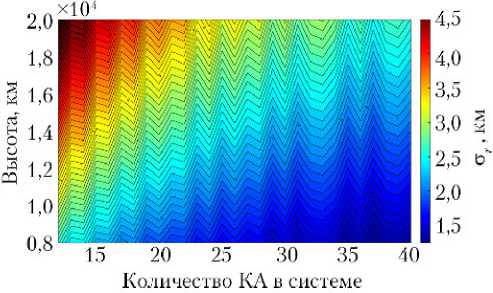
Рис. 3. Погрешность ст r наблюдений КПС на широте 45 °

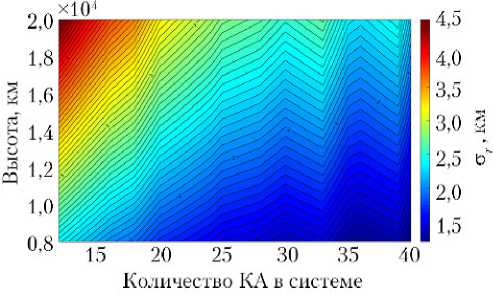
Рис. 4. Погрешность ст r наблюдений ОПС на широте 45 °

Численные значения соответствуют шкале цветов, расположенной справа от карт.

Эти же результаты представлены также в виде трехмерной поверхности на рис. 5 (КПС) и 6 (ОПС).

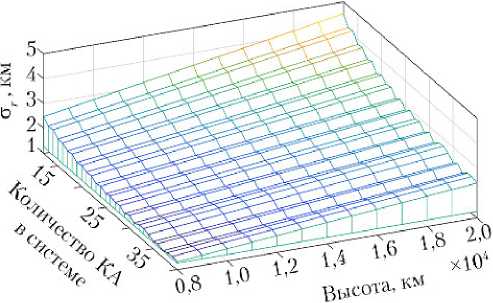
Рис. 5. Трехмерное представление изменения погреш ности стr наблюдений КПС на широте 45°

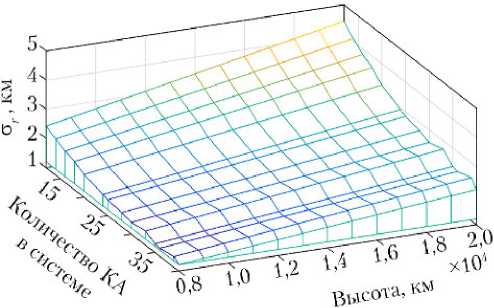
Рис. 6. Трехмерное представление изменения погрешности стr наблюдений ОПС на широте 45°

Анализ влияния кратности обзора и типа системы (КПС, ОПС) не выявил их существенного влияния на точностные характеристики. В качестве примера приведем возможные конфигурации ССН для N = 12, 24, 36 КА для рассматриваемых типов и указанных кратностей обзора при использовании одних и тех же высот орбит (это означает, что системы с одними и теми же N и h при различной кратности обзора будут иметь различающиеся минимальные углы возвышения над плоскостью местного горизонта). Характеристики систем представлены в табл. 1. Для представления структуры КПС используется система обозначений [8] в виде тройки целых чисел N/P/F, где N — общее количество КА в системе; Р — количество орбитальных плоскостей; F — фазовый сдвиг положений КА в смежных плоскостях. Последний параметр представляет целое число долей 2п/N. Около-полярные спутниковые системы являются несимметричными системами, для которых задаются сдвиг долгот восходящих узлов орбит АХ и фазовый сдвиг положений КА вдоль орбиты в смежных плоскостях [9].

Пропущенные в табл. 1 значения соответствуют сочетанию параметров, при котором не может быть образована система с положительными углами возвышения.

При моделировании оценивались минимальные, средние и максимальные погрешности наблюдения. В табл. 2 (КПС) и 3 (ОПС) приведены примеры изменения этих погрешностей при различных N и h

Выборка сводных характеристик различных ССН для систем двукратного обзора (при наблюдении объекта на широте 45°).

Предельно возможные минимальные значения погрешностей о _г достигают примерно –17% относительно средних значений. Максимальные значения могут отклоняться от средних на величину до 45%. Тип используемой системы (КПС или ОПС) также не оказывает значительного влияния. В табл. 4 представлены характеристики средних погрешностей для ССН с высотой h = 10 000 км при различных кратностях обзо-зора и широтах объектов наблюдения для N = 24.

Таблица 1

Тип ССН	Кратность	N	P	Сдвиг плоскостей АХ, °	Фазовый сдвиг		i	е	а
					F	Аф, °			h = 8 000 км	h = 10 000 км	H = 12 000 км	H = 15 000 км	H = 20 000 км
КПС	2	12	2	180	0	—	45,6	63,600	0,067	3,527	6,218	9,276	12,760
		24	2	180	0	—	45,3	49,300	15,377	19,110	21,919	25,014	28,422
		36	2	180	0	—	45,2	46,808	18,281	22,031	24,834	27,905	31,264
	3	12	4	180	2	—	59,9	70,811	—	—	—	1,840	5,257
		24	2	180	1	—	45,3	54,808	9,225	12,882	15,671	18,785	22,261
		36	2	180	1	—	45,2	49,200	15,492	19,226	22,034	25,129	28,536
	4	12	12	180	2	—	58,6	82,359	—	—	—	—	—
		24	2	180	0	—	45,2	63,469	0,198	3,662	6,355	9,414	12,899
		36	2	180	0	—	45,1	52,600	11,649	15,342	18,144	21,256	24,712
ОПС	2	12	2	109,91	—	51,84	61,67	63,89	—	3,230	5,916	8,971	12,453
		24	4	93,51	—	30,40	57,41	43,14	22,704	26,456	29,231	32,244	35,509
		36	6	62,7	—	4,78	68,46	36,34	31,415	35,075	37,729	40,559	43,571
	3	12	4	180	—		52,24	66,72	—	0,362	3,002	6,021	9,483
		24	4	180	—	30	46,92	50,76	13,712	17,429	20,237	23,342	26,773
		36	—	—	—	—	—	—	—	—	—	—	—
	4	12	—	—	—	—	—	—	—	—	—	—	—
		24	6	143,97	—	9,76	51,11	56,61	7,285	10,908	13,684	16,794	20,281
		36	—	—	—	—	—	—	—	—	—	—	—

Таблица 2

Таблица 3

Пример изменения погрешностей для КПС двукратного обзора при различных N и h

Пример изменения погрешностей для ОПС двукратного обзора при различных N и h

N	Тип погрешности	h, км
		8 000	10 000	12 000	15 000	20 000
12	мин.	2,0799	2,3696	2,6586	3,0913	3,8146
	ср.	2,4690	2,8124	3,1557	3,6697	4,5284
	макс.	3,3165	3,9106	4,5439	4,6509	5,7387
24	мин.	1,5145	1,7249	1,9353	2,2514	2,7777
	ср.	1,6869	1,9216	2,1564	2,5083	3,0952
	макс.	2,0521	2,2578	2,4838	2,937	3,7652
36	мин.	1,2411	1,4138	1,5861	1,8451	2,2768
	ср.	1,3759	1,5673	1,7587	2,0458	2,5242
	макс.	1,5366	1,8053	2,0097	2,3571	2,9083

N	Тип погрешности	h , км
		8 000	10 000	12 000	15 000	20 000
12	мин.	2,0021	2,2805	2,5587	2,9762	3,6719
	ср.	2,4216	2,7584	3,0955	3,6006	4,4426
	макс.	2,9517	3,6400	3,7927	4,4068	5,4377
24	мин.	1,4503	1,6513	1,8491	2,1507	2,6531
	ср.	1,5980	1,8203	2,0427	2,3762	2,9319
	макс.	1,7360	1,9970	2,2813	2,5806	3,1844
36	мин.	1,1873	1,3526	1,5178	1,7653	2,1782
	ср.	1,2683	1,4447	1,6211	1,8858	2,3269
	макс.	1,4175	1,6146	1,8118	2,1076	2,6005

Таблица 4

Характеристики средних погрешностей для ССН с высотой h = 10 000 км при различных кратностях обзора и широтах объектов наблюдения для N = 24

Тип	Кратность	Широта
		0°	45°	75°
КПС	2×	1,7664	1,9216	2,0979
	3×	1,7675	1,9221	2,0977
	4×	1,7668	1,9207	2,0984
ОПС	2×	1,7823	1,8203	1,7986
	3×	1,7844	1,8672	1,8751
	4×	1,7982	1,8021	1,8093

Незначительное повышение точности ОПС для средних и высоких широт (45 и 75 ° ) объясняется их особенностью — существенным повышением числа наблюдаемых КА в приполярных областях.

Характер изменений точности наблюдений в зависимости от высоты близок к линейному (см. примеры на рис. 5, 6). Причиной ухудшения точности при увеличении высоты является явная зависимость от дальности (2), которая в значительной степени определяется высотой. Это позволяет при начальном выборе параметров ССН использовать линейные оценки изменений погрешности ст r при вариации этого параметра относительно опорного значения. Так, для рассмотренного примера (N = 24) приближенное значение производной составляет r ≈ 0,000115 км/км. ∂h

Однако зависимость точности от количества КА в системе носит экспоненциальный характер. На рис. 7 показан характер этой зависимости для примера КПС с высотой h = 10 000 км.

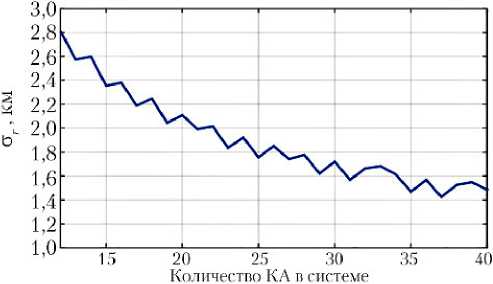
Рис. 7. Зависимость погрешности ст r от количества КА для КПС с h = 10 000 км

На рис. 8 показан характер этой зависимости для примера ОПС двукратного обзора с высотой h = 10 000 км.

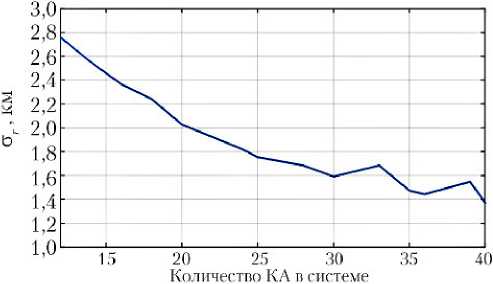
Рис. 8. Зависимость погрешности ст r от количества КА для ОПС с h = 10 000 км

Заключение

В статье предложен критерий точности для предварительного сравнительного анализа многоспутниковых систем непрерывного наблюдения Земли, основанный на положительно определенной матрице, описывающей геометрию ошибок и не зависящей от особенностей целевой аппаратуры.

Проведенное моделирование возможных конфигураций ССН по известным типам спутниковых систем непрерывного глобального обзора различных кратностей и для различных географических широт показало, что наиболее существенное влияние на точность наблюдений оказывают два параметра: высота орбиты и общее количество КА. Их влияние на точность близко к линейному.

Представленные результаты могут использоваться для предварительного выбора конфигурации ССН.