Критерий усталостного разрушения металлов при мало- и многоцикловом нагружении

Усталостные явления чрезвычайно многообразны, в связи с чем возникли различные научные направления, изучающие закономерности многоцикловой, малоцикловой, термической, ударной, коррозионной усталостей, фреттинг-усталости, а также поверхностного усталостного изнашивания.

В этих условиях знание степени циклической повреждаемости, мерой которой при эксплуатации по наработке может служить накопленное повреждение, а при эксплуатации по состоянию - параметры усталостной трещины, является необходимым элементом обеспечения в процессе эксплуатации требуемого уровня надежности и безопасности полетов. В зависимости от характера эксплуатационных неисправностей для оценки характеристик надежности по критерию сопротивления цикловой усталости используют различные подходы.

Расчет долговечности по критерию образования усталостной трещины при N< 105 осуществляется на основе кривых малоцикловой усталости [2; 11; 13; 17; 19]. В основу расчетных методов положена степенная зависимость Мэнсона-Коффина, связывающая число циклов с размахом пластической деформации [13]:

A e_pN m = C_f , (1) где m, C_f- характеристики металла. Так как размах полной деформации А е равен сумме размахов упругой А е ^ и пластической А е_р составляющих, то в зависимость (1) подставляется величина Ае_р = Ае- А е ^ .

Предполагая, что Ае^ не зависит от числа циклов и ее величина равна деформации на пределе выносливости при растяжении-сжатии, получают известное соотношение Б. Лангера [11]

А е =

1,1     2о !

In -----+----1

2 N 0 -5 1 -V E

Делая ряд допущений о зависимостях упругой и пла стической составляющих полной деформации от числа циклов нагружения, можно получить уравнение С. Мэн сона [11; 23]

л 1 I,      1

А e =      ln----

N 0 ^,6 1 1 -у

+

EN 0 _f ,12

При снижении температуры возрастает концентрация напряжений (рис. 1,2), изменяются соотношения между размахами упругой Аеу, пластической Аер и полной Ае деформациями и, соответственно, усталостные повреждения материала. Этот эффект уравнения (1) - (3) не описывают. Установлено, что если размахи составляющих полной деформации Аеу и Аер соизмеримые величины, то использование уравнений (1) и (2) для оценки долго вечности элементов приводит к существенному отклонению расчетных значений Nfот экспериментальных [16]. Представим деформационно-кинетический критерий усталостного разрушения [6; 18] в виде [7; 9]

НИИ , 1, (4) гдеП,П - соответственно доля повреждений от упругой и пластической составляющих полной деформации; П - доля квазистатических повреждений. Повреждения П_у вызваны местными неупругими сдвигами [15], межатомным внутренним трением [14], дефектом модуля упругости [3] и другими необратимыми процессами, не связанными с макропластическими деформациями [1]. Их интенсивность пропорциональна амплитуде действующих напряжений и обратно пропорциональна пределу выносливости материала. Доля повреждения П_р определяется размахом пластической деформации Ае_р и располагаемой пластичностью металла.

Как сами деформации, так и интенсивности полных, упругих и пластических деформаций обладают аддитивными свойствами [10]. Рассмотрим одноосное напряжен-

ное состояние. Можно показать, что в этом случае амплитуда интенсивности полной деформации е ^ вычисляется по формуле

^в

^в

где О - предел выносливости при базовом числе циклов N₀ ц - постоянная материала (0,1^^^0,15). Характеристика материала m может быть определена через значение на- 2 ( 1 + и ) S_{K        ЛТ} 1

пряжения S_K из условия 2 e ay =       — ^ПР^И / = 4 ,

_ ² ( 1 + ^и ) ° a

⁶ ia =      ЗЕ    ^{+ 6} ap ’

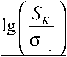
lg I N

тогда ц =

•

где О - амплитуда напряжений

Первое слагаемое представляет собой упругую е^, второе - пластическую е_ар составляющие е ^ .

Циклическая долговечность ^связана с амплитудой пластических деформаций степенным уравнением [13]

е_и = 1ln — N ^- m i ia 4 1 -v f

•

Показатель степени т. в первом приближении, принимаем равным 0,5. Тогда соотношение между амплитудой е_т и долговечностью N-имеет вид

Используя выражения (4)-(7), определяем усталостные повреждения, вызванные упругой и пластической составляющими амплитуды полной деформации Разрушающее число циклов ^находим по правилу линейного суммирования усталостных повреждений из условия достижения суммой повреждений предельной величины. Если доля квазистатических повреждений мала и ими можно пренебречь, то получим следующее уравнение:

mi

e ay

2(1 + и)о _{- 1} N ^ц N ^-ц ------------------------------------------------------------ ,

N f

I

e ap

11 ln

N f ( ^dN • I

1 _L

° a

° - 1 N о

dN = 1 •

3 E

а

б

1 -^

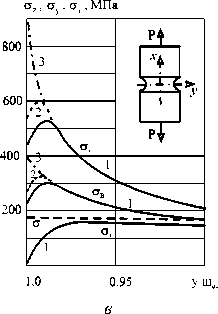
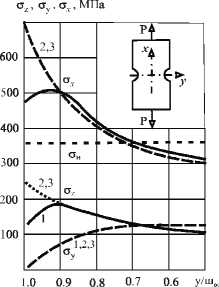
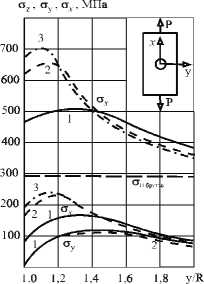
Рис.1. Распределение напряжений О ^ , О _у , О _г в сечениях (х = 0) при Т₀ = 293 К и низких температурах [9] для: а - пластины с боковыми надрезами (материал: Ст 45; а _о = 1,98; О _н = 0,9); 1 -Т₀ = 293 К; 2 -Т = 200 К; 3 -Т = 77К; б - пластины с круговым отверстием (материал: 12Х18Н10Т; а _о = 3; О _н 0,8); 1 - Т₀ = 293 К; 2 - Т = 200К; 3 - Т = 77 К;

в - стержня с круговым надрезом (материал: Ст 19Г; а _о = 5,1; О _н = 0,5); 1 - Т₀ = 293 К;

2 - Т = 200К; 3 - Т = 77 К

а                             б                              в

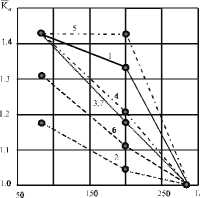
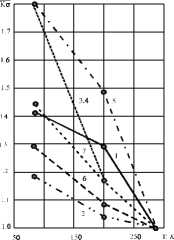
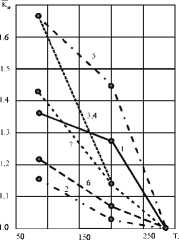
Рис. 2. Зависимости ^ , = [ ^ _о] _г/ Е ^ о ] _г 0 = _{293 к} от температуры [9] для: а - пластины с боковыми надрезами ( а _о= 1,98; О _н = 0,9) 1 - 12Х18Н10Т; 2 - 30ХГСА; 3 - Ст 30;

4 - Ст 19Г; 5 -Ст45;6- Д20; 7 - АТ-2; б - пластины с круговым отверстием ( а _о= 3; О _н = 0,8); 1 - 12Х18Н10Т; 2 - 30ХГСА; 3 - Ст 30; 4 - Ст 19Г; 5 - Ст 45; 6 - Д20;

7 - АТ-2; в - стержня с круговым надрезом ( а _о = 5,1; О _н = 0,5); 1 - 12Х18Н10Т;

2 - 30ХГСА; 3 -Ст30; 4 -Ст19Г; 5 -Ст45; 6 - Д20; 7 - АТ-2

В условиях малоциклового нагружения возможны промежуточные виды разрушения (между квазистати-

Коэффициенты концентрации интенсивности напря

ческим и усталостным типами). В этом случае в левую

жений К^ К₂, К₃ вычисляются как:

- линейная аппроксимация диаграммы деформиро

часть уравнения (8) добавляется доля квазистатического

ef de повреждения [2] ПS = — S

0 ° f

, где е - односторонне накоп

ленная деформация; е- односторонне накопленная деформация к моменту разрушения (появления трещины);

Е,^- располагаемая пластичность. Величина располагаемой пластичности вычисляется в зависимости от жестко

сти напряженного состояния.

Используя обобщенную диаграмму циклического деформирования, из выражения (8) получим уравнения кривой усталости при жестком (e . _a - const) и мягком ( О _а = const) нагружениях. Зависимость между напряжениями и деформациями в координатах S i = е( при упругопластическом деформировании в к-м полуцикле следующая [11]:

- при линейной аппроксимации диаграммы дефор

мирования

где E T ( к ) =

S⁽ k ) = 2 + ( е * - 2) E T ( к ) ,

-----—— -циклический модуль упрочнения;

1 ₊ CF ( ^к )

2 E T

- при степенной аппроксимирующей е ( к ) _ ^г-*( к )^{1 - ( к} ) Si —

зависимости

,

вания по формулам

2 N f

2 Nf J

1 + и

m i

^ dk ,

где n ( к ) =

lg e iⁿ

1g [ e n +    ( e -1 ) F ( к )

- показатель упроч-

2 N f

² = 2 N f !

2 N f

³ = 2 ^ 7 !

\

И i

(

— + l 1 - — E T ( к ) ак

ei

ei

О

-

1     1 - 2 ( 1 + и )

_° a E T ( ^к ) ° a ³

mi

;     (12)

ак ^;

- степенная аппроксимация диаграммы деформирования по формулам

2 N f                                 ¹

K = Л- Г 1 -1±»(2 с.)- '⁴- ¹      ;

1 2 N f 1 L 3 ^V J

2 N

2 N f

K 2 = 2 N J [ 2 0 e- )

n ( к ) - 1

^И i ак ,        (13)

2 N_f

K₃ =----- f (2o) - ( к )

³ 2 N f 1 ^a/

^{1 -} n ( ^к ) 2 ( 1 + u ) k

-

mi ак.

нения в e e = — eT

упругопластической области в полуцикле к;

- интенсивность деформаций при нагружении

материала из исходного состояния.

По S ^{( к} ) и е/ определяем следующие величины:

- ( к )

О a

о(к)    S( к)            е(к)

°a     S___ . -(к)    eia°

= п ; eia =

О t 2          Ст2

ё ^{( к} )=е^(к ’- 2(1 + ц)б^{( к} )

ap ia з

На основании соотношений (8) зависимости между напряжениями и деформациями и (9) запишем уравнения кривой усталости материала при жестком и мягком

нагружении:

- жесткое нагружение (е._а = const), равное

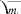
e ia e T

11 ln

( ^{4 1} -V J

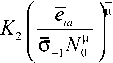
N f

(Ю)

- мягкое нагружение (s =

° a ° T

K 3

°-i ^гд^{е О} - 1 = _.

° T

const), равное

( ° a ^О - 1 )^И = 1

N 0      N f

Если повреждения П существенно меньше, чем Пу и ими можно пренебречь, то выражения (10) и (11) превращаются в обычное уравнение кривой усталости

° mN =° mN, a j -10, гдет- —.

И

Если пренебречь величиной повреждений Пу, то из выражения (6) получим степенную зависимость Мэнсона-Коффина.

Из критериального уравнения (8) следует, что традиционные методы расчета долговечности, основанные на определении местных напряжений, целесообразно использовать, когда усталостные повреждения от упругой составляющей деформации существенно больше, чем от пластической. В этом случае учет повреждений, вызванных пластической составляющей деформации, осуществляется вычитанием этих повреждений из суммы относительных повреждений ар, входящей в известные кинетические уравнения усталостных повреждений [4; 5; 12].

Приведем расчетные кривые усталости при жестком симметричном нагружении гладких образцов из сплавов Д16 и В95, полученные по зависимости Б. Лангера (2), С. Мэнсона (3) и уравнению (10), экспериментальные данные из работ [8; 16] (рис. 3).

Расчеты осуществляли при следующих данных: Д16-т , = 0,5, ц =0,12, V 25,2'+, о . 163МПа, X 10⁶; В95 - т' = 0,5, ц = 0,12, у = 16%, О _-1 = 171 МПа, X КХ Так как в зоне разрушения отсутствовали односторонне накопленные деформации, то доля квазистатического разрушения П - 0. Из полученных результатов следует, что кривые малоцикловой усталости, рассчитанные по уравнению (8), практически совпадают с экспериментальными, в то время как зависимости С. Мэнсона и Б. Лангера

дают существенное отклонение расчетных величин размаха деформаций Ве от данных эксперимента. Значения долговечности А найденные из решения уравнения (2), занижены, а из (3) - завышены, аналогичные результаты по (2),(3) получены в [20; 21].

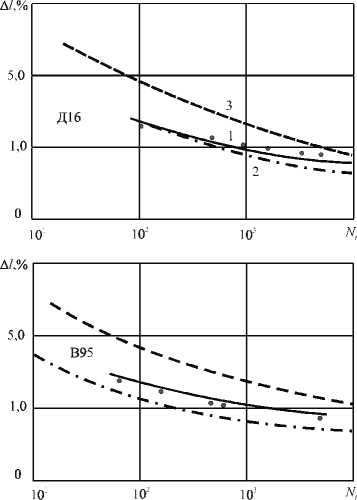
Рис. 3. Расчет кривых усталости при жестком нагружении: 1 - расчет по (10); 2 - расчет по Лангеру (2); 3 - расчет по Мэнсону (3); • - экспериментальные данные [8; 16]

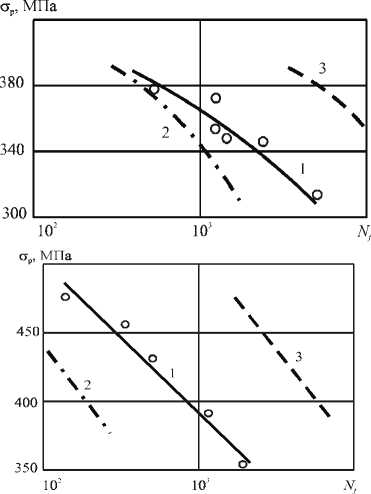
Рис. 4. Расчет кривых усталости при мягком нагружении: 1 - расчет по(11); 2 - расчет по Лангеру (2); 3 - расчет по Мэнсону (3); е - экспериментальные данные [8; 16]

Представлены кривые усталости при мягком симметричном нагружении гладких образцов из сплавов Д16и В95, полученные из уравнений (2), (3) и (11), а также кривые усталости, рассчитанные по уравнению (11), достаточно хорошо совпадают с экспериментальными точками, в то время как зависимости (2) и (3) дают существен ное отклонение расчетных амплитуд напряжений Оа от экспериментально установленных.

Использование уравнения (8) для прогнозирования долговечности конструктивных элементов требует установить соответствие между напряжениями и деформациями равной повреждаемости стандартного образца и элемента конструкции.