Критерий выбора оптимальной альтернативы по переводу судна из критического состояния в эксплуатационное

Борьбу с аварийностью по линии "человеческого фактора" необходимо вести на всех уровнях управленческой лестницы компаний. Ответственность за аварийность должна повышаться во всех звеньях аппарата управления и контроля. Вопросы повышения качества подготовки специалистов, ответственности за выдвижение, аттестацию кадров – насущные вопросы времени. Завеса "неуловимости и непостижимости" в "человеческом факторе" значительно развеется, если перевести разговор в плоскость конкретных проблем. Можно найти "неуловимость и непостижимость" лишь в отдельных проявлениях, например, в том, что одни только принимают решения, а ответственность за неправильные волевые решения несут другие. Некоторые аварии созревают буквально в тиши кабинетов, закладываются в безответственных, незрелых проектах, в завышенных нормативах. Однако в рамках теории фазовых переходов развитие любой аварии можно представить как взаимосвязь трех основных состояний организационно-технической системы управления безопасностью мореплавания и составить модель этих взаимосвязей (Сарлаев и др., 2009).

В данной работе рассматривается один из наиболее общих подходов к составлению модели динамики аварии, причем в основу этого похода положена априорная гипотеза, в которой предполагается, что основными состояниями аварийной организационно-технической системы являются эксплуатационное и аварийное состояния, а критическое состояние является лишь переходным, обладающим свойством бифуркации.

2.    Модель фазовых переходов состояний организационно-технической системы судна

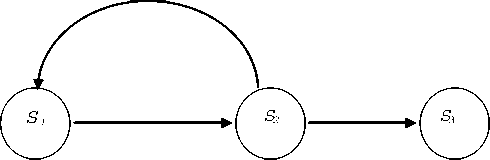
Взаимосвязи эксплуатационного, критического и аварийного состояний организационнотехнической системы несения вахты можно представить в виде направленного графа с циклической топологией G3 (S, W), где S – вершины графа, а W – его ребра (рис.). Основным устойчивым состоянием, отвечающим условиям безопасной эксплуатации судна, является эксплуатационное состояние, совпадающее с вершиной графа S1. В этом состоянии действия факторов опасности не значительны и сбалансированы действиями организа-

Вестник МГТУ, том 14, №4, 2011 г.   стр.740-742

ционно-технической системы на стадиях профилактики и предупреждения аварийности.

Если при выполнении судовых ключевых операций в организационно-технической системе факторы опасности создают реальную угрозу в эксплуатации судна, и действия таких факторов не могут быть сбалансированы на стадиях профилактики и предупреждения, то возникает не устойчивое (двойственное) критическое состояние, совпадающее с вершиной графа S ₂. Это состояние не устойчиво, поскольку, с одной стороны, способно при принятии организационно-технических мероприятий вернуться в устойчивое эксплуатационное состояние S ₁ (критичность без последствий), а с другой стороны, когда принятые меры не адекватны действиям факторов опасности, превратиться в аварийное состояние, совпадающее с вершиной графа S ₃ (критичность с последствиями).

Сутью критического состояния организационно-технической системы несения вахты является то, что для этого состояния характерно реальное или кажущееся нарушение ее функционирования, а так же разрушение отдельных ее элементов. Естественно, что в случае кажущегося нарушения функционирования или кажущегося разрушения элементов организационно-технической системы возможно возвращение этой системы в эксплуатационное состояние, обеспечивающее безопасность судну.

При истинном разрушении элементов или истинном нарушении режима функционирования организационно-технической системы аварийное состояние судовой ключевой операции уже необратимо. Свойство необратимости и устойчивости истинного аварийного состояния судовой ключевой операции в эволюционной модели взаимосвязи (рис.) закреплено в вершине графа S3. В истинном аварийном состоянии организационно-техническая система обязана реагировать на разрушительные действия опасных факторов, но лишь в том плане, чтобы локализовать, а в последующем и минимизировать последствия от этих действий.

3.    Выбор альтернативы минизизирующей вероятности больших затрат

Исходя из проблемы, возникающей при выборе и принятии однократных решений при риске, когда такой выбор приходится осуществлять исключительно среди альтернатив с потерями, целесообразно использование критерия выбора, который обеспечивал бы, насколько это возможно, уменьшение вероятностей возникновения больших потерь. В рамках данного подхода ниже дается решение задачи для случая, когда капитан судна (ЛПР) должен выбирать среди альтернатив вида ( Кини, Райфа , 1981)

A i = ( l i 1 , p i 1 , …; l ij , p ij , …), i = 1, 2, 3, …, n ,                                   (1)

где l ij – величина потерь, возникающих при j -м исходе альтернативы A i , p ij – вероятность j -го исхода альтернативы A_i .

Наиболее полную информацию относительно вероятностей возникновения больших потерь может содержать функция, записанная так pi(l) = p(ξi ≥ 1), где ξi – вероятностная переменная, выражающая величину потерь в случае реализации альтернативы Ai, а l – определенное значение величины потерь.

Уменьшение, насколько это возможно, вероятностей возникновения больших затрат можно осуществить в том случае, если капитан судна выбирает такую альтернативу A_i из (1), при которой было бы истинно следующее высказывание:

∀ l ∈ L          p ( l i ) = min p i ( l ),                                      (2)

i где L – область интересующих ЛПР значений l.

Для реализации критерия предположим, что вероятностные переменные, выражающие величину потерь в случае реализации альтернативы A_i , соответствуют следующим высказываниям:

∀ i,j ∈ I           ( D 1 ( i , j ) ∨ D 2 ( i , j ) ∨ D 3 ( i , j )),                                      (3)

где

D ₁ ( i , j ): ∀ l ∈ L имеет место p_i ( l ) ≥ p j ( l ),

D ₂ ( i , j ): ∀ l ∈ L имеет место p_i ( l ) ≤ p j ( l ), D 3 ( i , j ): ∀ l ∈ L имеет место p i ( l ) = p j ( l ).

Тогда при выполнении условий (3) критерий (2) может быть преобразован так

V l g L          p о ( l) = min p , (l ),                                      (4)

i а выбранная ЛПР альтернатива Ai является оптимальной.

Помимо требований, накладываемых на функцию p i ( l ), необходимых для реализации критерия (4), эта функция также должна отвечать условиям, вытекающим из ее определения, а именно:

0 <  p , (l) < 1                                                        (5)

и если l_A >  l B , то

Р ⁽ l A ) <  p ⁽ l B ).                                                       ⁽⁶⁾

Следовательно, критерий выбора наименее опасной и оптимальной альтернативы (4) в случае однократных решений при риске возможен, если существуют функции p i ( l), которые удовлетворяют требованиям (3), (5) и (6). Тогда сформулируем условия, при которых возможно существование функций p i ( l ).

Исходя из достаточно общих соображений функции p i ( l) = п( l , h i ), где h i - величина параметра h , должны подчиняться следующим требованиям. Функции p i ( l ) должны принадлежать такому классу G определенных на оси l функций п( l , h ) с параметром h , при котором истинна дизъюнкция вида

Fi(n) v F2(п), где

F 1 (п): если h a >  h b , то V l g L     n( l , h a ) >  n( l , h b ),

F ₂(п): если h a >  h b , то V l g L     n( l , h a ) <  n( l , h b ).

Кроме того, функции из класса G должны быть определены на интервале

0 <  п( l , h ) <  1, так, чтобы при l a >  l b выполнялись условия:

П( l a , h ) <  П( l b , h )

V l g L           n( l , h i ) - p , ( l) = min [n( l , h ) - p, ( l )]

hi∈H если

HA h | V l , g L n( l , h ) > p , (l )}.

Выполнение первого требования является необходимым и достаточным условием истинности высказывания (3). Выполнение второго и третьего требований необходимо и достаточно для того, чтобы функция p i ( l ) обладала свойствами (5) и (6). При формулировке последнего требования было принято во внимание условия в (3).

4.    Заключение

Выбор оптимальной альтернативы перевода судна из критического в эксплуатационное состояние при однократном решении капитана с учетом имеющегося риска возможен, если существуют такие ограниченные вероятностные функции от затрат, для которых существует структура порядка. Наличие этих функций при бифуркации критического состояния организационно-технической системы позволяет выполнить такой перевод при минимальной вероятности максимальных потерь.