Критические температуры смесей 1, 3-диметиладамантана и 1, 3, 5-триметиладамантана с толуолом. Методы прогнозирования критических температур бинарных смесей цикланов с углеводородами

ция практически отсутствует. Имеются лишь сведения, полученные нами ранее и представленные критическими температурами:

• ·    индивидуальных 1,3-диметиладамантана (1,3-ДМА) и 1,3,5-триметиладамантана (1,3,5-ТМА) [1],

• ·    смесей 1,3-ДМА и 1,3,5-ТМА с циклогексаном (ЦГ),

• ·    смесей 1,3-ДМА и 1,3,5-ТМА [2].

В настоящей работе экспериментально определены T_cm 1,3-ДМА и 1,3,5-ТМА с толуолом в полном диапазоне варьирования их составов.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Для проведения эксперимента использовали 1,3-ДМА и 1,3,5-ТМА с чистотой 99,9% (ГЖХ), методика синтеза описана в [1].

Критические (жидкость-пар) температуры определены ампульным методом по исчезновению мениска - при нагревании и появлению мениска - при охлаждении. Схема установки и процедура эксперимента приведены в [1]. Погрешность измерения Т_сm оценена в 0,7 К и включает инструментальную погрешность, погрешность эксперимента и воспроизводимость измерения.

Состав смесей до эксперимента определялся по соотношению масс компонентов. Взвешивание производилось на весах “SHIMADZU DEUTSCHLAND GmbH” модель AUW120D с точностью до 0,1 мг. Минимальная масса компонента составила 17,4 мг. Состав смесей после измерения критических температур определяли методом ГЖХ. Результаты приведены в табл. 1 и свидетельствуют о достаточно высокой терми-

Таблица 1. Результаты определения критических температур смесей

Содержани е w1/w2, масс. % Опыт, c мин. Tcm эксп., К E T cm, К До опыта После опытаb Толуол(1) + 1,3-Диметиладамантан(2) Tcm=x1?Tc1 + x2?Tc2 + x1? x2?(46,09 + 19,45?(x1 – x2) -39,38?(x1 – x2)2), R2=0,999 0,0/99,9 b 0,0/98,6 460 706,7 0 10,4/89,6 a - 280 688,3 1,0 24,0/76,0 a 24,0/75,5 170 676,6 10,7 33,0/67,0 a - 249 662,1 8,5 80,5/19,5 a 80,1/18,9 204 609,9 4,1 99,96/0,0 b 99,9/0,0 250 591,8 0 Толуол(1) + 1,3,5-Триметиладамантан(2) Tcm=x1?Tc1 + x2?Tc2 + x1? x2?(45,37 + 4,098?(x1 – x2) -13,78?(x1 – x2)2), R2=0,999 0,0/99,9 b 0,0/98,5 420 701,9 0 11,2/88,8 a 11,0/88,5 264 686,6 5,9 29,7/70,3 a - 234 662,6 9,7 46,6/53,4 a - 123 644,8 11,5 56,3/43,7 a 56,3/43,3 450 631,4 7,6 88,2/11,8 a - 467 601,2 2,1 99,96/0,0 b 99,9/0,0 250 591,8 0 a – состав определен весовым методом; b – состав определен хроматографическим методом, суммарная концентрация неидентифицированных компонентов составляет х= 100 – x1 – x2, %; с – время пребывания в области критической температуры (Tcm ±5ч7 К).

ческой стабильности изученных метиладаманта-нов в зоне их критических температур.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Полученные экспериментальные результаты принципиальным образом дополняют базу данных (табл. 2) по критическим температурам бинарных смесей цикланов с углеводородами различных классов, что дает возможность распространить выводы по результатам представленного ниже анализа не только на смеси с участием мо-ноциклических структур, но и на бинарные смеси углеводородов с каркасными соединениями.

Весь массив собственных и литературных данных был аппроксимирован уравнением Ред-лиха-Кистера [3]:

T cm = ^X 1 • T c 1 ⁺ x 2 • T c 2 ⁺ x 1 • x 2 ^ A ⁺ A 2 ^ ^X 1 ^- x 2 ^{) +} A 3 ' ( ^x 1 " ^x 2 ) 2 ) ,⁽¹⁾ где Т_с1, Т_с2 и T_cm – критические температуры чистых компонентов и бинарной смеси соответственно.

Уравнение Редлиха-Кистера удобно для хранения информации и сопоставления данных, оно часто применяется для этих целей. Наличие трех настраиваемых параметров в уравнении позволяет хорошо описывать эксперимент. Средние по модулю абсолютные отклонения, как правило, находятся в пределах погрешности измерения. Относительно сложный характер уравнения делает его чувствительным к объему выборок, использованных при аппроксимации.

Для анализа концентрационных зависимостей критических температур использовались избыточные критические температуры Т^Е_сm , которые расcчитывались по формуле [3]:

T E = T cm - ( X 1 • T c1 + X 2 • T c 2 ) • ⁽²⁾ где Т_сm – критическая температура смеси; Т_с1 Т_с2 – критические температуры индивидуальных соединений; х₁, х₂ – мольные доли компонентов смеси.

Полученные нами экспериментальные данные по Т_сm были проанализированы совместно с ранее исследованными системами ЦГ+1,3-ДМА и ЦГ+1,3,5-ТМА [1] и 1,3-ДМА+1,3,5-ТМА [2]. Зависимости избыточных критических температур приведены на рис. 1.

Значения T^E_cm смеси 1,3-ДМА+1,3,5-ТМА близки к нулю, зависимость Т_сm от состава, выраженного в мольных и массовых долях, имеет линейный вид. Для смесей 1,3-ДМА и 1,3,5-ТМА с толуолом значения T^E_cm находятся на одном уровне в пределах 1,5 К. Такая же картина наблюдается для смесей 1,3-ДМА+ЦГ и 1,3,5-ТМА+ЦГ, только уровень значений T^E_cm на по-

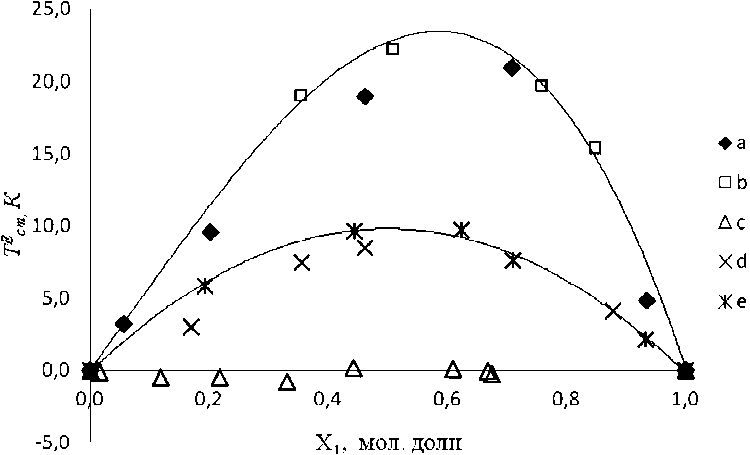
Рис. 1. Зависимости T^E_cm от состава смесей:

а – ЦГ + 1,3-ДМА [1]; b –ЦГ +1,3,5 –ТМА[1]; c – 1,3,5-ТМА + 1,3-ДМА [2]; d – 1,3-ДМА +толуол; e – 1,3,5-ТМА+толуол

рядок выше. Это говорит о том, что переход от одного метиладамантана к другому в ряду мети-ладамантанов не приводит к существенному изменению Т_сm , в то время как переход от ЦГ к толуолу влечет за собой существенные изменения. Экспериментальные данные по Т_сm смесей

ЦГ+1,3-ДМА и ЦГ+1,3,5-ТМА, дополняющие ряд смесей с циклогексаном, позволили увидеть тенденцию к увеличению T^E_cm при переходе от моноциклических алканов к трициклическим каркасным углеводородам.

На рис. 2 приведены зависимости T^E_cm от со-

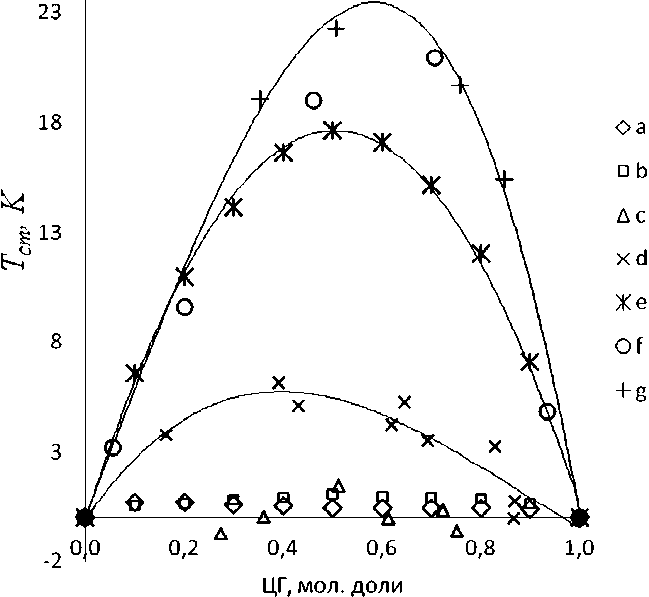
Рис. 2. Зависимости T^E_cm от состава смесей:

а – ЦГ+МЦП [4]; b – ЦГ+МЦГ [4]; c ^cm – ЦГ+Цгеп [4]; d – ЦГ+ЦО[4]; e – ЦГ+цис-декалин [4]; f – ЦГ+1,3-ДМА [1]; g – ЦГ+1,3,5-ТМА[1].

става смесей циклоалканов, таких как метилциклопентан (МЦП), метилциклогексан (МЦГ), циклогептан (ЦГеп), циклооктан (ЦО), цис -декалин.

На рис.2 видна четкая тенденция к увеличению T^E_cm при переходе в смеси ЦГ+Циклоалкан от циклогептана к 1,3,5-ТМА. Причем для смесей моноцикланов с близкой молярной массой избыточные значения Т_сm не превышают 2 К. Смесь ЦГ+ЦО характеризуется T^e_cm, достигающей 5 К, переход к цис -декалину приводит к увеличению этого значения до 17 К.

Отмеченный тренд аналогичен тенденциям, наблюдаемым в смесях ЦГ с алканами (рис. 3).

Переход в этом ряду от этана к декану влечет за собой двунаправленное изменение TEcm. Смесь ЦГ+Этан имеет максимальное значение TE = 48 К. С увеличением молярной массы ал-cm кана TEcm снижается и минимальное значение TEcm соответствует смеси ЦГ+н-Гексан, дальнейшее продвижение в ряду к смеси ЦГ+н-Декан приводит к увеличению TEcm до 12 К.

Для рассмотренных смесей зависимости Тсm от состава характеризуются несимметричным видом, причем при увеличении уровня избыточности Тсm наблюдается смещение максимумов на кривых TEcm. В связи с этим возникает проблема аппроксимации экспериментальных данных, т.к. подобная зависимость не будет корректно описываться квадратичными уравнениями даже в случае использования настраиваемых коэффи- циентов бинарных взаимодействий (КБВ).

На собственных и литературных данных для T_cm нами был протестирован ряд правил смешения, используемых для прогноза T_cm и аппроксимации экспериментальных данных. Апробации подверглись следующие правила: квадратичная форма правила Кея, оригинальная и модифицированная формы уравнений Ли-Кеслера, Хигаси, Ликмана-Эккертома-Праусница, Чью и Пра-усница, Ли [5, 6]. Эти правила смешения можно разделить на две группы: прогностические и с настраиваемым коэффициентом бинарного взаимодействия.

Прогностические правила смешения не включают в себя настраиваемые КБВ и минимальный набор исходной информации для этих методов представлен критическими температурами и критическими объемами индивидуальных соединений. К этой группе методов относятся: метод Ли и оригинальная форма уравнения Ли-Кеслера.

Остальные перечисленные правила смешения требуют настройки КБВ и относятся к второй группе. Путей для применения моделей, использующих КБВ, два.

При обработке небольшого количества экспериментальных точек T_cm правилами смешения второй группы возможна оценка T_cm для смеси любого состава. В случае отсутствия экспериментальных значений T_cm с их помощью можно оценить значения критических температур смеси,

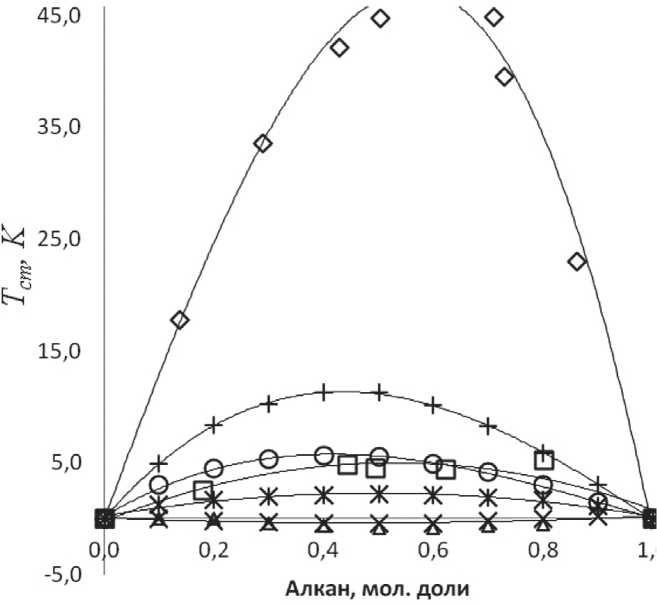
Рис. 3. Зависимости T^E_cm от состава смесей:

а – ЦГ+этан [4]; b – ЦГ+н-пентан [4]; с – ЦГ+н-гексан [4];d – ЦГ+н-гептан [4]; е – ЦГ+н-октан [4]; f – ЦГ+н-нонан [4]; g –ЦГ+н-декан [4]

имея информацию о коэффициентах бинарного взаимодействия. Наилучшие значения КБВ получаются обратным пересчетом из экспериментальных данных методом последовательных приближений.

Нахождение зависимости КБВ от отношения критических объемов ( V_ci /V_cj ) предложено в [5] для квадратичной формы правила Кея. Нами этот метод распространен на другие правила смешения.

Правило Кея является наиболее простым из всех предложенных на данный момент правил смешения, в нем Т_сm определяется как сумма ее мольных составляющих [6]. Расчет Т_сm этим методом, за исключением некоторых случаев, не дает удовлетворительных результатов, особенно если компоненты смеси разной природы или являются полярными и склонными к ассоциации [6]. Модификацией рассматриваемого правила является его квадратичная форма:

T cm = У ТЛ^.. T k M, (3) где k_ij – коэффициент бинарного взаимодействия.

Оригинальная форма правила смешения Ли-Кеслера [6] помимо критических температур индивидуальных соединений включает в себя критические объемы. Уравнение имеет вид:

Tcm = ^ЕЕXxИ3 + V13У TT , (4) 8Vcm ij где Vcm – критический объем смеси, Vci , Vcj – критические объемы индивидуальных компонентов смеси.

Это правило было модифицировано в работе [7] путем введения коэффициента бинарного взаимодействия kij в уравнение (4)

T cm = ЕЕ k f^M ⁺ '^ТТ .(5)

8 V_{cm ij}

Оригинальный вид правила смешения Ли-Кеслера является прогностическим, при введении kij уравнение становится апроксимацион-ным, но его работоспособность увеличивается.

Чью и Праусниц [6] в предлагаемом методе используют поверхностные доли 6 j .

xV ²³

Tcm = Е jj + ЕЕ ^ем . 6 = v;N , (6) j ij ∑ x i V ci

i где т j - параметр взаимодействия, получаемый по экспериментальным данным.

Подход c использованием поверхностных долей предложен Хигаси [8] и описывается уравнениями:

T cm = 6 1 T c 1 + e ₂ T c 2 + 2 O ₁ 0 2 A t ; 6 1 = V ci _2/3 , (7) ∑ x j V ci j = 1

где A t - коэффициент бинарного взаимодействия.

Выражение состава через объемные доли применяется в подходах Ли и Ликмана-Эккер-тома-Праусница. Метод Ли является прогностическим и не включает в себя настраиваемые параметры. Уравнение имеет вид:

T cm = Е^ф j T cj . ^Ф i = V x i V jr .      (8)

j               ∑ x j V cj

j

Правило смешения Ликмана-Эккертома-Праусница включает в себя настраиваемый параметр k_ij^L :

T cm = ЕЕ ф• ф j T cj , где ф | = xXV cT- , (9) ij                ∑ x j V cj

j тсу=(i - kL s'TiT-cj )^/2.          (io)

По полученным нами и литературным данным проведено тестирование правил смешения. Основные результаты тестирования представлены в табл. 2.

Проанализировав таблицу, можно сделать следующие выводы:

• -    уравнение Редлиха-Кистера хорошо описывает имеющиеся экспериментальные данные по Т_сm , за исключением смесей ЦГ с метаном, этаном. Смесь ЦГ+метан плохо поддается аппроксимации и прогнозированию. Источник отклонений пока неизвестен.

• -    аппроксимационные модели с настраиваемым параметром бинарного взаимодействия работают на уровне погрешности эксперимента;

• -    из прогностических методов лучшие результаты, так же как и для смесей алканов, дает метод Ли.

Работа выполнена при финансовой поддержке Минобрнауки РФ (г.к. №16.552.11.7016 от 29.04.2011 г.) с использованием научного оборудования ЦКП “Исследование физико-химических свойств веществ и материалов”.