Критическое смещение атома и коэффициент Пуассона неорганических стекол

В последнее время наблюдается заметный интерес к взаимосвязи между коэффициентом Пуассона (коэффициентом поперечной деформации) и рядом структурно-чувствительных свойств материалов, в частности, свойств, связанных с тепловыми колебаниями атомов в решетке [1-12].

В теории упругости он определяется отношением поперечной деформации тела sz=Ad/d0 к его продольному удлинению ex=A1110 при одноосном растяжении: ц—sz/sx. Коэффициент Пуассона отражает не только характер прямой деформации в направлении действия внешней силы, но и особенности поперечной деформации, происходящей в направлении, не совпадающем с направлением действия внешней силы. Поперечная деформация sz определяется свойством тела передавать внешнее воздействие в других направлениях, что зависит от атомно-молекулярного строения тела и динамики решетки.

Из известного уравнения для параметра Грюнайзена yd, характеризующего ангармонизм колеба ний решетки, следует, что функция коэффициента Пуассона (1-2ц) выражается через физические ве личины, связанные с тепловыми колебаниями атомов в решетке и с температурой Дебая 9 [3],

1 - 2 ц =

a EV

^Y D^CV

где а - коэффициент линейного теплового расширения, Е - модуль упругости, C V - теплоемкость .

Д.З. Батлаев, С.Ш. Сангадиев, В.В. Мантатов и др. Критическое смещение атома и коэффициент Пуассона неорганических стекол

Как показано в [3], для изотропных структур с гранецентрированной и объемноцентрированной кубическими решетками зависимость (1-2 р ) от 0^ m/T_e оказывается линейной (точки на графиках ложатся на прямые, m – атомная масса, T e – температура испарения). Это означает, что величина (12 р ) есть фактически функция среднеквадратического смещения атома из равновесного положения <  A r²_m>, ибо произведение ® тесно связано с <  A r²_m>.

Аналогичная зависимость коэффициента Пуассона р от среднеквадратичного смещения атомов <^{A r}m >  имеет место и в случае изотропных стеклообразных систем [5,13]. За меру <^{A r}m >  можно

принять аналогичную характеристику, а именно элементарный флуктуационный объем

Au = п d2 Ar

e

m

,

необходимый для критического смещения атома A r m , соответствующего максимуму силы межатомного притяжения [14, 15] ( n d² - площадь эффективного сечения атома).

Флуктуационный объем аморфной системы обусловлен критическими смещениями кинетических единиц из равновесных положений

A V = N Au e ee ^, где N e – число возбужденных (критически смещенных) атомов. Кинетическая единица (атом, группа атомов), способная к критическому смещению, названа "возбужденным атомом", а сам подход – моделью возбужденного состояния (моделью делокализованных атомов, если под делокализацией атома понимать его критическое смещение из положения равновесия).

Флуктуационный объем A V e , по существу, совпадает с флуктуационным свободным объемом аморфных веществ V f = N h ^ v h , поскольку элементарный объем Au e можно интерпретировать как объем флуктуационной дырки u h , куда может перескочить соседняя частица ( N h - число флуктуационных дырок) [15]. Следует заметить, что пустой статический объем между молекулами по Ван-дер-Ваальсу, который называют иногда структурно-обусловленным [16], геометрическим [17] свободным объемом, практически не имеет никакого отношения к флуктуационному (свободному) объему [15].

Настоящее сообщение посвящено исследованию связи коэффициента Пуассона со структурночувствительными параметрами модели возбужденного состояния, а именно с элементарным объемом возбуждения атома Au e и долей флуктуационного объема в области стеклования f g = ( A V_c/V)_T = _Tg.

Коэффициент Пуассона и критическое смещение атома

В модели возбужденного состояния [15] доля флуктуационного объема f= A V e V определяется формулой

, AU f =---- exp u

—

As _e + P Au _e kT

где и = V / N - атомный объем, Ag e - энергия возбуждения атома, k - постоянная Больцмана. Разрешив это уравнение относительно давления Р и полагая постоянство параметров модели, возьмем производную от давления по температуре при постоянном объеме

dP ^ _ k In (1/ f ) dT ) V     Au e

,

где учли, что объемы Av e и и по порядку величины близки. Из термодинамики известно, что эта производная равна произведению коэффициента объемного теплового расширения 0 на изотермический модуль объемного сжатия В

V

.

В свою очередь данное произведение можно выразить из уравнения Грюнайзена следующим образом

в В = Y u

, где cV – теплоемкость, отнесенная к атому.

Из последних трех соотношений (3)-(5) находим относительный объем атомного возбуждения (критического смещения атома)

Au e = k ln(1 f)

u      cVYD

Если примем приближенное условие стеклования f=fg® const при T= Tg [17, 18] и предположим, что в стеклообразном состоянии выполняется закон Дюлонга и Пти cV=3k, это выражение упрощает- ся

AU e = In (V /, )

^{U        3} Y D

.

Воспользуемся формулой Беломестных-Теслевой [6]

• 3 Г 1 + ц )

Y „ = — I I

D

• 2 ( 2 - 3 ц J

которая позволяет оценить параметр Грюнайзена y d из данных о коэффициенте Пуассона ц . Полагая ln(1/ f _;) ~ 3 и используя (7) в (6), приходим к заключению, что коэффициент Пуассона является функцией относительного объема атомного возбуждения

• 2 - 3 ц

  U ^A U e

  ^{J u} .                                   (8)

  
  

• 1    + ц

Отсюда следует, что зависимость (2-3 ц )/(1+ ц ) от отношения ( Au e / u ) должна быть линейной, что в самом деле подтверждается для силикатных стекол (рис.)

Г 2 - 3 ц |     Г Au e I

I 1 + ц J ~ I u J .                                (9)

Здесь относительный объем ( Au e / u ), необходимый для возбуждения атома, был рассчитан по данным о микротвердости H V и модуле упругости при одноосной деформации Е [19, 20]

Au e ^ 6 H V u E

Полученный результат (9) означает, что коэффициент Пуассона ц определяется главным образом критическим смещением атома из равновесного положения A r m ~Au _e, соответствующим максимуму силы межатомного притяжения.

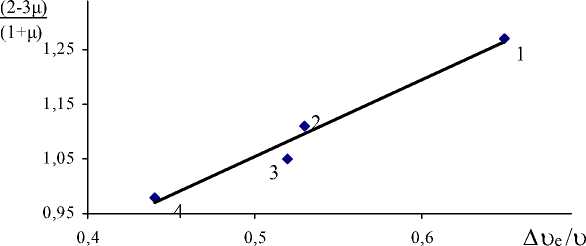
Рис. Зависимость функции коэффициента Пуассона (2-3μ)/(1+μ) от относительного объема возбуждения атома Au _e/ u для силикатных стекол. 1 - кварцевое стекло, 2-4 - натриевосиликатные стекла Na₂O-SiO₂, содержание Na 2 O, мол.%: 2 – 16, 3 – 20, 4 – 33.3.