Криволинейные пьезоэлектрические актюаторы изгибного типа с управляемой формой поперечного сечения

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2025PNRPU MECHANICS BULLETIN

Пьезоактивные композиты с пьезоэлектрическими и/или магнитострикционными элементами структуры используются в современных интеллектуальных конструкциях в качестве функциональных элементов: преобразователей, датчиков, актюаторов [1-5], функционирующих на основе эффектов связанностей деформационного, электрического и/или магнитного полей. Математическое моделирование свойств и поведения пьезоактивных композитов основывается на постановке и решении связанных краевых задач электромагнитотер-моупругости для микронеоднородной представительной области с использованием методов механики композитов [6-9]. Гибкие биморфные пьезоэлектрические актюаторы состоят, как правило, из двух или более однородных пьезоэлектрических слоев (пластин, пленок) равной толщины с одинаковой или взаимообратной поляризацией слоев, межслойных и наружных электродов [1017]. Такие пьезоэлектрические актюаторы имеют малый вес, низкое потребление энергии, хорошую гибкость и силовое воздействие на управляемые объекты и находят широкое применение в конструкциях аэрокосмической техники, например, в спутниковых антеннах, солнечных панелях и гибких связях функциональных элементов робототехнических устройств [18-22], в частности, для выполнения функций регулировки ориентацией и управления движением спутника по заданной траектории, широко используются в микроэлектронике и атомно- силовых микроскопах [23; 24]. Гибкие пьезоэлектрические биморфы используются в качестве генераторов электрической энергии [13; 25-29], датчиков [12; 30; 31] и актюаторов - пьезоэлектрических преобразователей электрических сигналов от источника питания в движение (микроперемещение), манипулирования или сборки микромасштабных объектов [11; 12; 14; 17; 32-40], в частности, пьезоэлектрических шаговых двигателей [33], микрозахватов [35], элементов управления геометрией отражающих [17] или аэродинамических [38; 40] поверхностей в современных микроэлектромеханиче-ских системах (МЭМС), системах автоматического управления радиотехники, электроники, оптики, аэрокосмической и медицинской техники. Гибкий биморф-ный пьезокантилевер [11; 34] работает как исполнительный механизм (актюатор) и, одновременно, как датчик самоконтроля - мониторинга информации о текущем значении действующей на кантилевер внешней силы и/или смещения (прогиба). Многослойные гибкие биморфы используют для повышения чувствительности -отношения величины изгибных деформаций биморфа к приложенному на электроды управляющему электрическому напряжению, в частности, когда отражающая поверхность деформируемого зеркала расположена на внешней стороне одного из слоев биморфа [17]. Пьезоактюатор с управляемой жесткостью на изгиб [41] представляет собой многослойный пакет из элементарных биморфных слоев с управляемой механической связанностью между смежными слоями. Достижение результирующего значения квазистатической изгибной деформации актюатора [41] осуществляется в резонансном изгибно-колебательном режиме – циклическом чередовании «активного» (в требуемом направлении изгиба) и «реактивного» (в обратном направлении) полупериодов колебания при малой и большой связанности элементарных слоев и, как следствие, при малой и большой результирующей изгибной жесткости многослойного пакета (актюатора) соответственно. Можно отметить исследование [42], где предложен гибридный пьезоэлектрический актюатор изгибного типа, который включает в себя две пьезоэлектрические секции – центральную круговую биморфную секцию «инициации» изгиба и периферийное «кольцо поджатия» с общим внутренним круговым электродом и различными для каждой секции внешними управляющими электродами. «Кольцо поджатия», как часть актюатора [42], примыкает к неподвижно (шарнирно или жестко) закрепленному его периметру и обусловливает существенное улучшение его изгибных характеристик.

В [43; 44] предложены криволинейные стержневые пьезоэлектрические актюаторы изгибного типа: кру-тильно-изгибный TorsBC-актюатор [43; 45] и изгибные актюаторы с управляемыми трансформациями форм своих поперечных сечений [44]. TorsBC-актюатор имеет вид криволинейного двухслойного «биморфа кручения», в частности, из двух пленочных пьезоэлектрических IncIDE-актюаторов [46] с ориентационными углами ± π/4 встречно-штыревых электродов (IDE); рабочий изгиб TorsBC-актюатора в поперечной плоскости обусловлен управляемым пьезоэлектрическим закручиванием его вокруг продольной криволинейной оси. В [44] требуемый изгиб криволинейных стержневых PlatCB ( Plate Curvilinear Bimorphic) или TubCB (Tubular Curvilinear Bi-morphic) актюаторов в продольной плоскости возникает опосредованно от управляемого пьезоэлектрического изменения начально-прямоугольной формы поперечного сечения к выпуклой «арочной» или двояковыпуклой «чечевичной» формам соответственно. Этот эффект обусловлен появлением распределенных по длине криволинейных актюаторов неуравновешенных изгибающих моментов, действие которых частично распрямляет, т.е. уменьшает значение начальной кривизны продольной оси актюатора, в результате управляемой трансформации формы его поперечного сечения. Наиболее существенно этот эффект проявляется для TubCB - актюатора с трансформацией прямоугольной формы тонкого составного двухслойного сечения к двояковыпуклой «че-чевично»-трубчатой форме по отношению к характеристикам традиционных прямолинейных или криволинейных TorsBC [43; 45] и PlatCB-актюаторов.

Цель исследования – разработка математической модели и изучение эффекта взаимодействия начальной кривизны и пьезоэлектрических трансформаций форм поперечных сечений криволинейных пьезоэлектрических PlatCB, TubCB-актюаторов [36] изгибного типа для улучшения их изгибных характеристик – увеличения максимальных смещений и блокирующих усилий, производимых актюаторами в рабочей продольной плоскости.

Биморфные криволинейные актюаторы

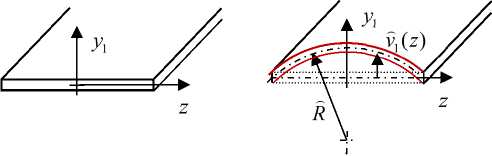
В начальном состоянии PlatCB-актюатор (рис. 1) представляет собой тонкий криволинейный стержень в виде тонкой биморфной цилиндрической пластины ленточного типа с прямоугольным поперечным сечением и управляющими электродами. Поляризация пьезоэлектрических слоев и расположение электродов биморфной пластины таковы, что при подключении к электродам управляющего электрического напряжения U _con тонкое прямоугольное сечение биморфа изгибается в плоскости своего поперечного сечения (а не в рабочей продольной плоскости, как это происходит в традиционных биморф-ных актюаторах изгибного типа), т.е. становится выпуклым «арочным» по всей длине пластины (ленты). «Двухслойный» трубчатый TubCB-актюатор (рис. 2) образован соединением по внешнему контуру двух пластинчатых PlatCB-актюаторов с возможностью трансформации составного тонкого прямоугольного поперечного сечения в двояковыпуклое «чечевично»-трубчатое сечение при подключении к электродам управляющего электрического напряжения U _con .

b

Рис. 1. Начальная ( а ) и выпуклая «арочная» ( b ) формы поперечного сечения биморфного слоя PlatCB-актюатора

Fig. 1. Initial ( a ) and convex "arched" ( b ) shapes of cross-section of bimorph layer of PlatCB-actuator

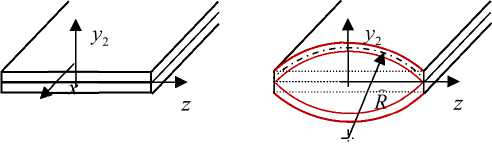
Рис. 2. Начальная двухслойная ( а ) и двояковыпуклая «чечевичная» ( b ) формы поперечного сечения TubCB-актюатора

Fig. 2. An initial two-layer ( a ) and biconvex "lentil" ( b ) shapes of cross-sectional of TubCB-actuator

Считаем, что PlatCB (см. рис. 1) и TubCB (см. рис. 2) актюаторы имеют начальный радиус кривизны R0 и консольно закреплены при x = 0 (см. рис. 3); размеры тонкого прямоугольного поперечного сечения: ширина b, толщина h = h1 с областью значений координаты У1 е (-h /2; h /2) для PlatCB-актюатора (см. рис. 1) и h = 2h1, у2 е (-h1; h1) для «двухслойного» TubCB-актюатора, где x е (0; l) - продольная координата, z е (-b / 2; b /2), h1 - толщина биморфного слоя (в целом, включая пьезоэлектрические элементы и электроды биморфа), l – длина актюатора в виде дугообразного стержня. Биморфный слой (см. рис. 1, а) или слои (см. рис. 2, а) трансформируют первоначально прямоугольные формы поперечных сечений в выпуклую (см. рис. 1, b) или двояковыпуклую «чечевичную» (см. рис. 2, b) формы в плоскости yz соответственно. Слои TubCB-актюатора скреплены между собой лишь по боковым сторонам своих периметров, при этом каждый слой – это биморфная двухслойная пластина толщиной h1 = 2ha, где ha – толщина каждого (например, в виде пленочного MFC (Micro-Fiber Composite) актюатора [47; 48] осевых по z перемещений) из обоих слоев биморфа.

а                                 b

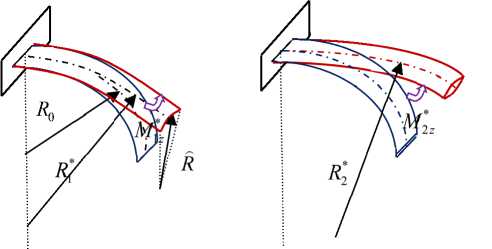
Рис. 3. Начальные и результирующие криволинейные формы PlatCB ( а ) и TubCB ( b ) актюаторов

Fig. 3. Initial and resultant curvilinear shapes of PlatCB ( a ) and TubCB ( b ) actuators

Математическое моделирование деформирования криволинейного актюатора

Рассмотрим построение математической модели деформирования криволинейных PlatCB и TubCB актюаторов через моделирование эффекта взаимодействия управляемых формоизменений их поперечных сечений и начальной кривизны 1/R0 продольной оси с целью увеличения изгибных характеристик – максимальных смещений и блокирующих усилий актюаторов в своей рабочей продольной плоскости. Изгиб PlatCB-, TubCB-актюаторов в продольной плоскости имеет реактивный характер как реакция на управляемые пьезоэлектрические (биморфные) формоизменения – вспомогательные изгибы их сечений в поперечной плоскости. При подключении к электродам биморфа управляющего электрического напряжения Ucon возникает пьезоэлектрический «биморфный» момент Mx , который изгибает первоначально прямолинейное (прямоугольное) сечение биморфа в плоскости y1,2z до радиуса кривизны R с функцией прогибов V1 2, в частности, для однослойного PlatCB-актюатора (см. рис. 1, b) в виде

—

— — M 2 Ь v1 = v1( z) = ——(z - ),          (1)

2 E z J x 1        4

для двухслойного TubCB-актюатора (см. рис. 2, b) имеем зеркальные (относительно срединной линии сечения) прогибы обоих верхнего и нижнего биморфных слоев v =f vi(z), у2 е (0;hi)

^v2 I^- v i ⁽ z ), у 2 ^{е ( -} h i ;⁰),

где J_x 1 = lh 1³ /12 - осевой момент инерции сечения, E z -поперечный модуль Юнга (по оси z ) биморфа, изгибающий момент

- U

M. « егЛ l — x zzz a

^A a

(как два слоя MFC-актюаторов [47; 48] толщиной h_a , расстоянием A a между соседними разнополярными встречно-штыревыми электродами и результирующим рабочим пьезомодулем e_zzz при поляризации пьезоэлектрического слоя по оси z ), радиус кривизны

- EJ, E hk r _ z x 1 ^ z 1 a

~ M ~3 e U x zzz con

В результате изгиба биморфа (в поперечной плоскости y1,2z) каждая точка его поперечного сечения с первоначальными координатами (y1,2 ;z) приобретает новые значения координат (y1 2; z) в главных осях инерции (проходящих через центр тяжести) искривленного сечения, в частности, для однослойного PlatCB-актюатора (см. рис. 1, b) имеем у1(У1,z) = У1 + -1(z)- У1 c, (5)

где y _{1 c} – координата центра тяжести искривленного в виде арки поперечного сечения, у 1 е ( - h /2; h j / 2) и для двухслойного TubCB-актюатора (см. рис. 2, b ) –

У 2 ( У 2 , z ) = У 2 + V 2 ( У 2 , z )                  (6)

или с учетом (1), (2) в виде

- , . f У 2 + V 1 ( z ), У 2 е (0; h j у. ( У. , z ) _

²         I У 2 - - 1 ( z ), У 2 е ( - W

Такие трансформации формы (см. рис. 1, 2) поперечных сечений в предположении неизменности положения

(на дуге радиусом R ₀ ) центра тяжести поперечного сечения при его трансформации с прямоугольного (см. рис. 1, а , рис. 2, а ) соответственно в выпуклое «арочное» (см. рис. 1, b ) или двояковыпуклое «чечевичное» (см. рис. 2, b ) обусловливают возникновение удлинений Д ( dl ) элементарных с начальной длиной dl 0 = ( R 0 + y₁₂ ) d 0 продольных (т.е. расположенных вдоль оси x ) «волокон» биморф-ного слоя, в частности, для однослойного PlatCB-актюатора

Д(dl) = (Rо + y + V - yc) d0-(Rо + yi) d0 = (у - yic)d0 , продольных деформаций

Д(dl) =  - У1 c dlо    Ro + yi и осевых напряжений

О

V           V

E ^V i — y i c ~ E ^V i — y i c x R о + y i ~ x R o

Аналогичные выражения запишем для двухслойного

TubCB-актюатора – ной схеме – дугообразный (длиной l) консольный стержень с радиусом R0 с «арочным» или «чечевичным» поперечным сечением с действующим на свободном торце результирующим изгибающим моментом M1*z или M2*z соответственно (см. рис. 3). Результирующий изгибающий момент M1*,2z частично распрямляет, т.е. уменьшает значение начальной кривизны дугообразного стержня (актюатора), увеличивая начальное значение R0 его радиуса до R* > Ro.

В частности, для TubCB-актюатора выражение (10) может быть преобразовано к виду

* ME 2 b -_/xw

^M 2 z = „ _F J ^{( z -} И У 2 ^{+ V} i ^{( z} )) ^ds i

R 0 E z J x 1 S ₁        4

или

^M 2* z = E ^- J ^{( Z 2 -} b -⁾⁽ У 2 ^{+ V} i ^{( z} )) ^ds i R ₀ R_{S 1}       4

с учетом радиуса кривизны R = E _z J _x 1 / M x или в виде

Д ( dl ) = ( R _o + y ₂ + V ₂) d 0-( R _o + y ₂) d 0 = V ₂ d 0,

продольных деформаций

^M 2* z =       ⁽ I i ⁺ I 2 ),

R 0 R

и осевых напряжений

Д ( dl ) =    v ₂

dl о ~ R о + y 2

где

I i = J У 2 ⁽

z ²

S 1

22 b /2

^- 7) ds i = T J ^{( z}

-t

b /2

b ²

7) ^dz =

b ³ h ₁ ²

12,

о = E xx

V v2

^R 0 ⁺ y 2

V

« E* — xR ₀

I, = ' f( z ² - — ) ² ds, = ² 2 R 4 ¹

S ₁

b /2

— I ( z

2R J

2 ^R - b /2

-

b ² ₄) ² dz

b ⁵ h ₁

60 R

в приближении y _{i 2} / R _о <<  i, т.е. имеем равенство R _о + y _i 2 ~ R _o, где E x — продольный модуль Юнга биморфа.

В результате в каждом сечении теперь уже «арочно»-пластинчатого PlatCB или «чечевично»-трубчатого TubCB стержня (актюатора) возникает соответствующий результирующий изгибающий момент, в частности, для PlatCB-актюатора

M * z = J о х У 1 ds = Er J ( ^_ i — y i c )( y i + V i - y i c ) ds i , ⁽9)

S 1 R 0 S 1

где прямоугольная область интегрирования S ₁ сечения: y 1 e ( - h 1 / 2; h 1 / 2), z e ( - b /2; b / 2); и аналогично для TubCB-актюатора с учетом симметрии его «чечевичного» сечения

^M 2* z = J ^О x ^yds = 2Ex- J ^V p ^{( z )(} у 2 ^{+ V} i p ^{( z} )) ^ds i , ^(1о) S R 0 S 1

где прямоугольная область интегрирования S ₁ : y ₂ e (о; h 1 ), z e ( - b / 2; b / 2). То есть приходим к расчет-

2 b ²

^{( z -} 7^).

с

учетом (1) величины прогибов ^_ 1 ( z ) = -2 R

В результате возникающий в каждом поперечном сечении дугообразного TubCB-актюатора результирующий изгибающий момент

E b ³ h ² b ⁵ h

M, „ = xv (---- + 1) 2z R0R 12   60R или в виде

E b ³ h ² b ² m_2z = ——V (i +—_ ) 2 z

обусловливает частичное разгибание стержня, т.е. происходит увеличение его радиуса кривизны с начального R ₀ до результирующей величины

R

*

1 - Mi

R ₀ E_x J ₂

или в виде

с учетом (14), (15) решений для блокирующих сил

*         R 0

R 2 —              ,

1 - Л а₂ / а₀

Ml где Ла2 — —2Z--угол поворота свободного торца, рав-

ExJ2z ный изменению угла охвата, дугообразного (длиной l) консольно-закрепленного стержня при его деформировании моментом M2*z , J2*z – осевой момент инерции «чечевичного» трубчатого сечения (см. рис. 1, b). Радиальное перемещение v2*r – прогиб центра тяжести свобод-

*

P *2 , =------- ------- v -1’,2 r ,              (19)

R o3 ( “ o - 2sin2 a o )

где прогибы на свободном торце

M ^* R ²

1,2 z 0

v 1,2 r ^— _{c T}*   ^{(1 -} cos ^a 0 ),

ExJ1,2z результирующий изгибающий момент для случая

первого

ного торца (по нормали к продольной оси x ) при x — l дугообразного TubCB-актюатора рассчитываем

Ehb

^M 1 z ^— -^

( ь ²       1 b 4

y ¹ c I 6 R ⁺ y ¹ c) 120 R ²

,

* M ^* R ²

v 2 r ^—      _r- ^{(1 -} cos ^a 0 )

E_xJ _{2 z}

по методу интегралов Мора, а блокирующая такой v ₂ ^* _r прогиб (при допуске углов поворота сечения) радиальная сила, приложенная на свободном торце,

*

P * —-------p^----- v * r          (15)

R 0 ^{( a} o ^- 2^{sin2 a} o ⁾

с учетом решения (14); величина блокирующего (прогибы и углы поворота всех сечений актюатора) изгибающего момента - M _{2 z} .

Коэффициенты эффективности актюаторов

Коэффициенты деформационной эффективности

^Z v 1,2 = v i*,2 r / v 1,2 r                         ⁽¹⁶⁾

предложенных PlatCB (см. рис. 1, рис. 3, а ) и TubCB (см. рис. 2, рис. 3, b ) актюаторов (относительно традиционных биморфных актюаторов изгибного типа) рассчитываем по аналогии с (14) через соответствующие значения прогибов

MR ²

v 1,2 r — _; ,     (1 - cos a o )              (17)

ExJ1,2z центра тяжести свободного торца (x — l) традиционных пьезоактюаторов с прямоугольным поперечным сечением, где осевые моменты инерции J1 z — bh3/12, J2z — bh3/12 c учетом h — 2h1. Аналогично (16), (17) рассчитывали коэффициенты силовой (блокирующей) эффективности

Z P 1,2 - P *2 r / P ,2 r — M *,2 z / M 1,2 z           (18)

вид M ₂ ^* _z определен ранее в (12). В выражении (21) величина y _{1 c} – координата центра тяжести «арочного» поперечного сечения, которая является функцией геометрических параметров: b , h ₁ – ширины и толщины и R – радиуса дуги срединной линии арочной формы поперечного сечения биморфной пластины (пьезоактюатора) как функции от управляющего электрического напряжения U _con и рассчитывается y 1 c — 5 1* _z / 5 1 через статический момент инерции S ₁ ^* _z «арочного» сечения в виде кольцевого сектора. Для традиционных биморфных актюаторов изгибного типа (например, также с использованием высокоэффективных MFC-актюаторов, но с поляризацией пьезоэлектрических слоев вдоль оси x ) изгибающие в продольной плоскости xy _1,2 моменты M _{1,2 z} в (17), (18) рассчитываются для первого случая – биморфа толщиной h ₁ по формуле

U

M_iz — eh.b~, 1 z xxx a

^Л a

—    ,^ b т.е. имеем M1 z — Mx^ c учетом (3) и для второго слу- чая – биморфа толщиной 2h1 (т.е. для случая удвоенной толщины ha — 2 ha — h1 MFC-актюатора) -

M 2 z — 4 M 1 z                 (23)

при поляризации пьезоэлектрического слоя MFC-актюатора по оси x с результирующим рабочим пьезомодулем e _xxx , равным величине e_zzz в формуле (3).

Результаты численного моделирования

На рис. 4–6 представлены результаты расчета пьезоэлектрического (изгибающего биморфный слой в поперечной плоскости) момента Mlx (3) (см. рис. 4), результирующих моментов M1*,2z (9)–(12) (см. рис. 5), изгибающих консоли RibBC (см. рис. 5, а) и TubCB (см. рис. 5, b) актюаторов в продольной плоскости, и радиальных перемещений v1*,2r свободного торца консоли PlatCB (см. рис. 6, а) и TubCB (14) (см. рис. 6, b) актюаторов в зависимости от значений приложенного к электродам управляющего электрического напряжения Ucon при толщине h1 = 2ha = 0,6 мм, ширине b = 20 мм, длине l = 100 мм, угле обхвата α0 =π/3 и начальном радиусе кривизны продольной оси R0=l/ α0 актюаторов при различных значениях расстояния ∆a между соседними электродами (в MFC-слоях биморфа); при этом продольный Ex = 10 ГПа и поперечный Ez = 5 ГПа модули Юнга биморфа, пьезомодуль ezzz = 15,8 Кл/м2 (PZT-5) (3). На рис. 7 даны графики результирующего изгибающего момента M2*z (12) (рис. 7, а, c, e) и радиального перемещения v2*r (14) свободного торца (рис. 7, b, d, f) консоли TubCB-актюатора в зависимости от геометрических параметров: α0 , b, h1 при неизменных значениях: Ucon = 1500 В, α0 =π/3 , b = 20 мм, l = 100 мм, h1 = 0,6 мм и вариации величины ∆a .

M _x , Нмм

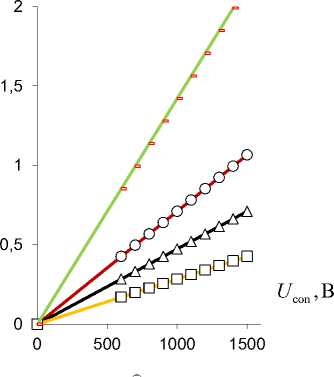
Рис. 4. Пьезоэлектрический изгибающий момент M _x биморфного слоя в зависимости от управляющего электрического напряжения U _con при ∆ _a =0,1 (-), 0,2 (○), 0,3 (Δ), 0,5 (□) [мм]

• Fig. 4.    Piezoelectric bending moment M _x of bimorphic layer depending on control voltage U _con at ∆ _a = 0.1 (-), 0.2 (○), 0.3 (Δ), 0.5 (□) [mm]

  M _{1 z} , Нмм

  

  а

  
  
  

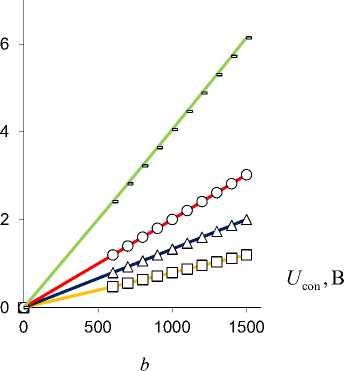
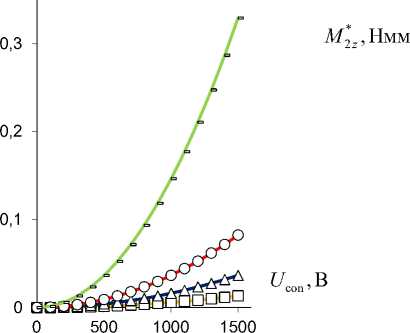
  Рис. 5. Результирующие изгибающие моменты M ₁ ^* _{,2 z} консоли RibBC M ₁ ^* _z ( а ) и TubCB M ₂ ^* _z ( b ) актюаторов в зависимости

  
  

от управляющего электрического напряжения U _con при ∆ _a =0,1 (-), 0,2 (○), 0,3 (Δ), 0,5 (□) [мм]

• Fig. 5.    Resultant bending moments M ₁ ^* _{,2 z} of RibBC M ₁ ^* _z ( a ) and TubCB M ₂ ^* _z ( b ) cantilever beam actuators depending on control voltage U _con at ∆ _a = 0.1 (-), 0.2 (○), 0.3 (Δ), 0.5 (□) [mm]

  *

  v _{1 r} , мм

  

  0,8

  0,6

  а

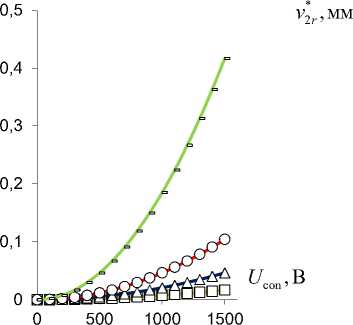
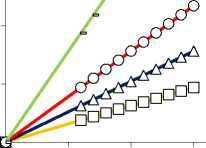
  Рис. 6. Радиальные перемещения v ₁ ^* _{,2 r} свободного торца консоли RibBC v ₁ ^* _r ( а ) и TubCB v ₂ ^* _r ( b ) актюаторов

  
  

  0,4

  0,2

  

  и ,в con ^,

  0 500 1000 1500

  b

  
  

в зависимости от управляющего электрического напряжения Ucon при ∆a =0,1 (-), 0,2 (○), 0,3 (Δ), 0,5 (□) [мм]

Fig. 6. Radial displacements v1*,2r of free end face of RibBC v1*r (a) and TubCB v2*r (b) cantilever beam actuators depending on control voltage Ucon at ∆a = 0.1 (-), 0.2 (○), 0.3 (Δ), 0.5 (□) [mm]

M _{2 z} ,Нмм

M _{2 z} ,Нмм

c

а                                          b

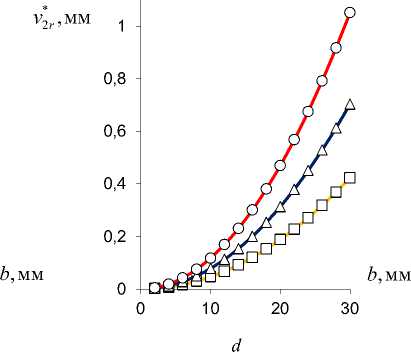
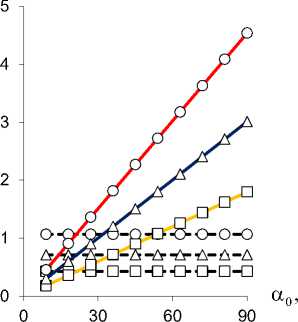
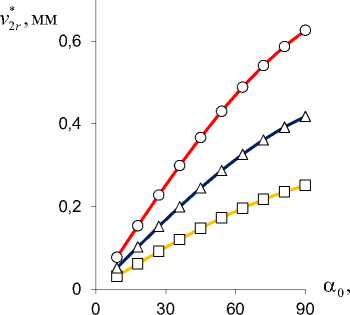
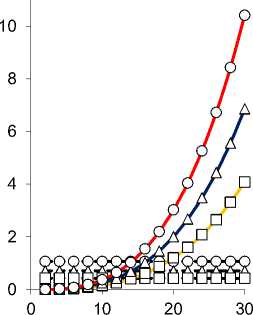
Рис. 7. Результирующий изгибающий момент M ₂ ^* _z ( а, c, e ) и радиальные перемещения v ₂ ^* _r свободного торца ( b, d, f ) консоли TubCB-актюатора в зависимости от параметров: α 0 , b , h 1 при ∆ a = 0,2 (○), 0,3 (Δ), 0,5 (□) [мм]; изгибающий момент M _x биморфного слоя (пунктирная линия)

Fig. 7. Resultant bending moment M ₂ ^* _z ( a, c, e ) and radial displacements v ₂ ^* _r of free end face ( b, d, f ) of TubCB-actuator cantilever beam depending on parameters: α 0 , b , h 1 at ∆ a = 0.2 (○), 0.3 (Δ), 0.5 (□) [mm]; bending moment M x of the bimorphic layer (dotted line)

, г*

M _{2 z} ,Нмм

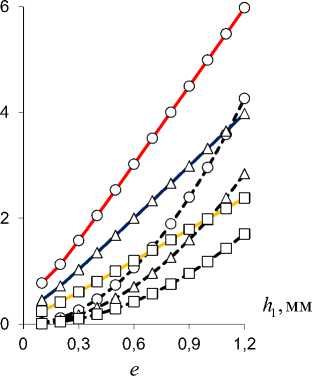
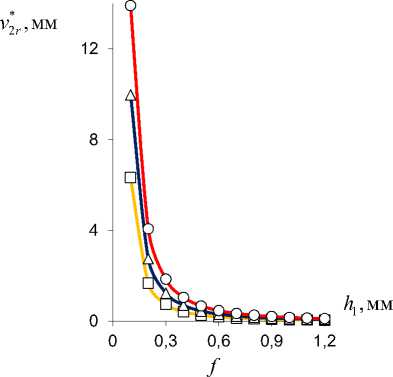
Рис. 7. Окончание

Fig. 7. The end

ζ

^ζ v 2

3,49

3,48

3,47

500 1000 1500

U con , В

ζ

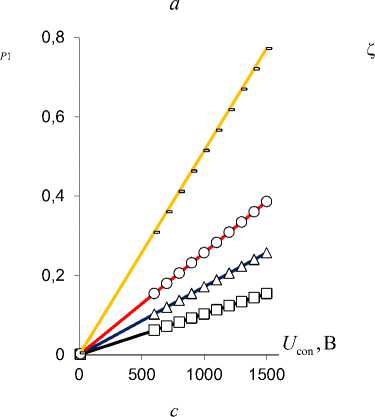
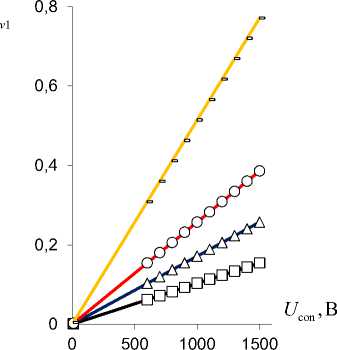
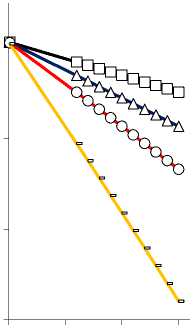
Рис. 8. Зависимость коэффициентов деформационной ζ _{v 1,2}

3,46

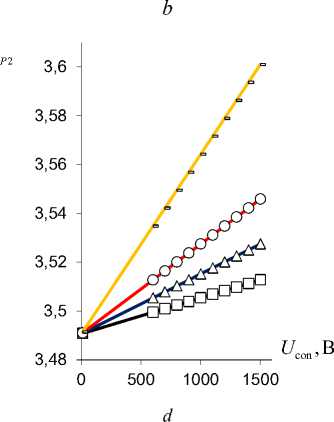
( а , b ) и силовой (блокирующей) ζ _{P 1,2} ( c, d ) эффективности

PlatCB ζ _{v 1} ( а ), ζ _{P 1} (в) и TubCB ζ _{v 2} ( c ), ζ _{P 2} ( d ) актюаторов в зависимости от управляющего электрического напряжения U _con при ∆ _a =0,1 (-), 0,2 (○), 0,3 (Δ), 0,5 (□) [мм]

Fig. 8. Dependence of coefficients of deformation ζ _{v 1,2} (a, b) and power (blocking) ζ _{P 1,2} (c, d) efficiency of PlatCB ζ _{v 1} (a), ζ _{P 1} (c) and TubCB ζ _{v 2} (b), ζ _{P 2} (d) actuators depending on control voltage U _con at ∆ _a = 0.1 (-), 0.2 (○), 0.3 (Δ), 0.5 (□) [mm]

а                                                               b

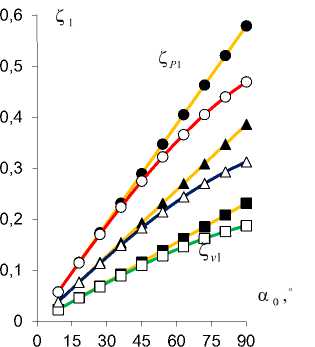
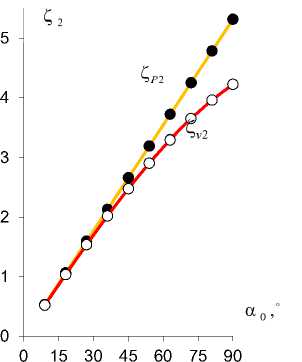
Рис. 9. Зависимость коэффициентов деформационной ζ _{v 1,2} (○, Δ, □) и силовой (блокирующей) ζ _{P 1,2} (•,▲,■) эффективности PlatCB ζ v 1 , ζ P 1 ( а ) и TubCB ζ v 2 , ζ P 2 ( b ) актюаторов в зависимости от угла α 0 при ∆ a = 0,2 (○), 0,3 (Δ), 0,5 (□) [мм]

Fig. 9. Dependence of coefficients of deformation ζ _{v 1,2} (○, Δ, □) and power (blocking) ζ _{P 1,2} (•,▲,■) efficiency of RibBC ζ _{v 1} , ζ P 1 ( a ) and TubCB ζ v 2 , ζ P 2 ( b ) actuators depending on the angle α 0 at ∆ a = 0.2 (○), 0.3 (Δ), 0.5 (□) [mm]

На рис. 8 приведены графики зависимостей коэффициентов деформационной ζ _{v 1,2} (16) (рис. 8, a, b ) и силовой (блокирующей) ζ _{P 1,2} (18) (рис. 8, b, d ) эффективности PlatCB ζ _{v 1} (см. рис. 8, а ), ζ _{P 1} (см. рис. 8, с ) и TubCB ζ _{v 2} (см. рис. 8, b ), ζ _{P 2} (см. рис. 8, d ) пьезоактюаторов в зависимости от управляющего электрического напряжения U con при фиксированном угле обхвата α 0 =π /3 , а на рис. 9 даны зависимости коэффициентов ζ _{v 1,2} , ζ _{P 1,2} PlatCB (см. рис. 9, а ) и TubCB (рис. 9, b ) актюаторов (16), (18) в зависимости от угла α 0 (т.е. от начального радиуса R 0 = l / α 0 ) при значениях: h 1 = 0,6 мм, b = 20 мм, l = 100 мм и вариации величины ∆ _a . Выявлено, что для актюатора TubCB (см. рис.9, b ), в отличие от RibBC (см. рис. 9, а ), имеем единые кривые зависимостей коэффициентов ζ _{v 2} , ζ P 2 от величин α 0 , R 0 при вариациях значений ∆ a .

Таким образом, в результате численного моделирования (рис. 4–9) выявлен монотонно возрастающий характер зависимости вспомогательного пьезоэлектрического инициирующего Mx (см. рис. 4) и результирующих реактивных M1*,2z (см. рис. 5) изгибающих моментов, прогибов v1*,2r (см. рис. 6) от величины управляющего электрического напряжения U con , при этом для величин Mix (см. рис. 4), M 2*z (см. рис. 5, b), v* r (рис. 6, b) зависимости от значения U con близки к прямым пропорциональностям. Уменьшение расстояния между электродами ∆a в MFC-биморфах в составе PlatCB и TubCB актюаторов приводит к увеличению как Mx (см. рис. 4), так и величин M1*,2z (см. рис. 5), v1*,2r (см. рис. 6). Увеличение значения начальной кривизны κ=1/R0=α0/l (см. рис. 7, а, b) и/или ширины b (рис. 7, c, d), в общем, для обоих PlatCB, TubCB-актюаторов приводит к монотонному увеличению величин результирующих моментов M1*,2z и прогибов v1*,2r (см. рис. 7, a–d) при постоянстве значения вспомогательного пьезоэлектрического инициирующего момента Mx – пунктирные линии на рис. 7, a, c. Увеличение толщины биморфного слоя h1 приводит к монотонному увеличению как вспомогательного пьезоэлектрического инициирующего момента Mx (пунктирные линии на рис. 7, e), так и результирующего реактивного изгибающего момента M2*z по близкой к прямой пропорциональной зависимости (рис. 7, e). Для величины прогиба v2*r (см. рис. 7, f) наблюдается обратная – монотонно-убывающая – зависимость от величины h1 , что обусловлено более значительным (по отношению к росту величины момента M2*z ) увеличением значения осевого момента J2*z (12), (14) и, как следствие, увеличением жесткости сечения на изгиб. Отметим, что с увеличением толщины биморфного слоя h1 также предполагается увеличение толщины ha = h1 /2 каждого его MFC-слоя, что обусловливает рост величины пьезоэлектрического момента Mx (3) и осевого момента инерции Jx1 (4). Выявлено, что наиболее существенно исследуемый эффект взаимодействия трансформации поперечного сечения с начальной кривизной продольной оси актюатора изгибного типа проявляется в увеличении рабочих характеристик для TubCB-актюатора с трансформацией прямоугольной формы его тонкого сечения к двояковыпуклой «чече-вично»-трубчатой форме (см. рис. 8, b, d, рис. 9, b).

Заключение

Разработаны математические модели деформирований криволинейных актюаторов: пластинчатого PlatCB и трубчатого TubCB [44] изгибного типов на основе эффекта взаимодействия двух связанных процессов: активного – управляемого пьезоэлектрического трансформирования формы поперечного сечения и реактивного – перехода актюатора к новой равновесной криволинейной форме с целью увеличения его изгибных характеристик – максимальных смещений (14) и блокирующих усилий (15) актюаторов в рабочей продольной плоскости (16), (18) (см. рис. 8, 9). Рассмотренные криволинейные