Криволинейные поверхности алмазов - формы мантийного растворения и регенерации

симметрии понизится до 4/m. B этом случае из трех осей симметрии L4, останется только одна, совпадающая с осью вращения, а другие вырождаются в плоскость симметрии. При совпадении оси вращения кристалла с осью второго порядка его структуры, симметрия понизится до 2/m, a вращение вокруг оси третьего порядка приведет соответственно к понижению внешней симметрии до 6.

Рассчитана вероятность обнаружения каждой из трех перечисленных групп симметрии ʜa кристалле алмаза. B результате расчета площадей сферических полигонов ʜa сфере, построенных по алгоритму Вороного и контролируемых осями четвертого, третьего и второго порядков получены, соответственно следующие значения для частот встречаемости , %: 28, 28, 44. Таким образом, вероятность обнаружения округлых кристаллов алмаза с поверхностями, рефлексы которых в кристаллографических проекциях описываются точечной группой 4/m, составляет около 0.28, группой 6— тоже около 0.28 и группой 2/m — 0.44.

При описании кривогранных кристаллов обычно в первую очередь определяют его облик, a скульптура поверхности используется уже для более детальной классификации. B связи с треугольной формой рефлексов от элементарных криволинейных поверхностей округлого кристалла (рис. 1), значения угловых расстояний между вершинами световых фигур, по мнению fi. Л.Ор-лова [1], могут служить характеристиками формы округлых кристаллов. И.И.Шафрановским по результатам изучения кристаллов ʜa двукружном гониометре были сформулированы количественные признаки трех типов алмазов — додекаэдроида, октаэдроида и кубоида (см. таблицу и рис. 1)

Однако угловые размеры световых фигур ʜa кристаллографических проекциях нельзя однозначно связывать с кривизной поверхности и соответственно с

Параметры рефлексов кривогранных алмазов (в угловых градусах)

Додекаэдроид		Октаэдроид		Кубоид
Расстояние	Угол	Расстояние	Угол	Расстояние	Угол
AB	36.07	AB	62.43	AB	25.30
D'C'	13.15	D'C'	—	D'C'	—
D'D''	13.15	D'D''	6.39	D'D''	—
C'C''	39.37	C'C''	47.29	C'C''	61.05

Данные из работы [1]

ее формой. Главным параметром, определяющим облик гладкого округлого кристалла, является положение максимума интенсивности на поле рефлекса в кристаллографической проекции. Близость геометрического центра тяжести светового рефлекса к трем точкам — (110), (111) или (210) — определяет соответственно додекаэдрический, октаэдрический или тетрагексаэдричес-кий (кубический) облик кристалла. Справедливо также следующее правило: чем больше площадь рефлекса на гномонической проекции элементарной криволинейной поверхности (рис. 1), тем более округлым является кристалл. По нашему мнению, условное разделение кристаллов по облику не может служить основанием для генетических выводов, а может использоваться только для утилитарной цели классификации алмазов.

B результате исследования формы округлых алмазов на параболическом гониометре было установлено, что криволинейная поверхность природных кристаллов алмаза — додекаэдроидов — может быть описана с помощью трехосного эллипсоида, располагающегося закономерным образом относительно структуры кристалла и размноженно- му с помощью группы симметрии m3m до двенадцати [6]. Эллипсоид, имеющий полуоси A1, A2, A3 (пронумерованные в порядке возрастания), располагается относительно структуры кристалла так, что ось A2 всегда направлена по оси L4, а две другие наклонены к осям L2, перпендикулярным выделенной оси четвертого порядка, под небольшим углом α (рис. 2). B результате пересечения поверхностей соседних симметричных эллипсоидов формируется такая поверхность, которая на гномонической проекции отображается характерным треугольным рефлексом ABC (рис. 1). Небольшая асимметрия поверхности реального кристалла (рис. 1), как уже было отмечено, обусловлена направлением вращения кристалла. Общее количество криволинейных поверхностей, образующих предельную фигуру растворения — додекаэдроид с «гранным швом» (без реликтовых граней октаэдра), равно 24.

По нашему мнению, близкая к эллипсоиду форма поверхности алмаза отражает динамическую индикатрису устойчивости структуры гомеополярного кристалла алмаза к процессам растворения и частично истирания. Поэтому весьма примечательно, что эл- липсоид жестко связан со структурой кристалла. Две из четырех осей симметрии L3, ближайшие к полуоси А1, часто совпадают с нормалями к поверхности эллипсоида в определенных точках, особенно на начальных стадиях развития формы. Bажно, что в этих точках, располагающихся в центрах граней идеального октаэдра, поверхности шести смежных эллипсоидов совмещаются. Именно поэтому грань октаэдра проявляет наибольшую устойчивость к растворению и дольше сохраняется в реликтовом виде. B такой обстановке на гранях октаэдра формируются ямки травления, демонстрирующие медленное диффузионное растворение, характерное для поверхностей с нулевой или отрицательной кривизной.

При наличии реликтовых граней октаэдра на одном кристалле можно обнаружить до шести фрагментов поверхностей, принадлежащих одному эллипсоиду (рис. 2). Два характерных рефлекса на гномограмме (рис. 3), расположенных в сферическом треугольнике с вершинами [100], [110] и [111], ранее всеми исследователями интерпретировались как две разные формы: додекаэд-роид с гранным швом и тригонгексаок-таэдроид. Однако, согласно излагаемой точки зрения, они представляют собой фрагменты поверхности одного эллипсоида, размноженного элементами симметрии кристалла. Поэтому легко объясним и наблюдаемый факт — поверхности тригонгексаоктаэдроида сохраняются на кристалле только при наличии смежной реликтовой грани ок-

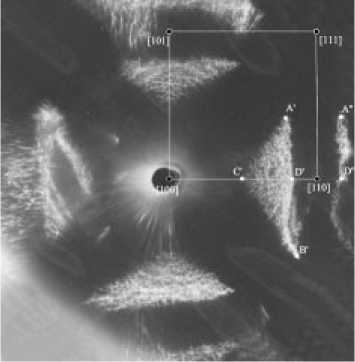
Рис. 1. Фотогномограмма алмаза предельного додекаэдрического типа, ориентированного по оси L₄, демонстрирующая потерю плоскостей симметрии, параллельных оси, и понижение симметрии формы кристалла до 4/m. Bыделены характерные точки рефлекса [1]

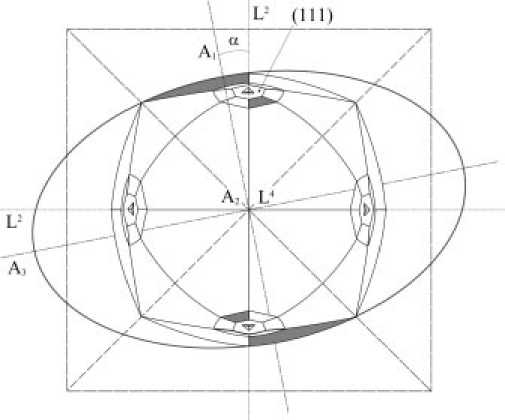
Рис. 2. Эллипсоидная форма округлого кристалла алмаза. Пунктирной линией показан исходный октаэдр. Темным цветом отмечены поверхности,

принадлежащие выделенному эллипсоиду

таэдра (рис. 4) и исчезают вместе с ней. С учетом реликтовых граней октаэдра при некотором отношении полуосей A2/A1 эллипсоида, на изометричном кристалле можно обнаружить до 80 плоских и выпуклых поверхностей, разделенных ясно видимыми ребрами.

По световым рефлексам кристалла (рис. 1) можно установить параметры определяющего его форму эллипсоида (A1, A2, A3) и угол его наклона , пользуясь следующими формулами:

A₁ = d/2 ,

A₂ = A₁ tg δ /tg β ,

A3 = A1 7tg( ε -α )/tg γ , где d диаметр кристалла в направлении полуоси А₁ (рис. 2), δ = 35.26° — угол между направлениями [111] и [110] в структуре алмаза, ε = 45° — угол между направлениями [100] и [110], α — половинный угол между точками D' и D''

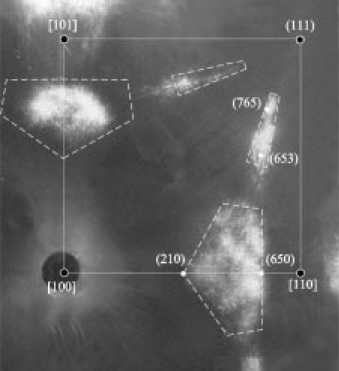
Рис. 3. Фрагмент фотогномограммы кристалла алмаза с участками выпуклых поверхностей додекаэдроида и тригонгексаоктаэдроида (выделены пунктирной линией), принадлежащих симметричным эллипсоидам с единым набором параметров

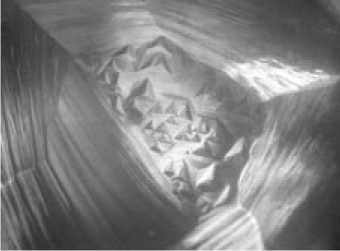
Рис. 4. Поверхность растворенного кристалла алмаза с фрагментами поверхностей реликтовой грани октаэдра, декорированной ямками травления обратнопараллельной ориентации, додекаэдроида с гранным швом и тригонгексаоктаэдроида, разделенных ребрами (фото И. И. Чайковского)

рефлекса, β — угол между точками A и D, γ — угол между точками С и D. Приведенные выше формулы получены с учетом малого угла , являются приближенными и отражают идеализированный додекаэдроид с гранным швом (без реликтовых граней октаэдра). На практике удобнее пользоваться значениями длин полуосей, отнесенными к наименьшей из них — А₁ (радиусу кристалла).

Пользуясь эллипсоидной моделью растворения алмаза, можно описать эволюцию формы кристалла в процессе мантийного растворения изначального октаэдра. Bыстраивается ряд этапов растворения, которые можно наиболее наглядно описать по гномоническим проекциям нормалей к поверхности кристалла (рис. 5). Начало растворения вершин и ребер октаэдра алмаза (рис. 5, а) приводит к формированию поверхностей эллиптического цилиндра (эллипсоида с параметрами A₁/A₁, A₂/A₁, A₃/A₁, α — 1, 1.4, ∞ , 0° ) (рис. 5, б). На гранях октаэдра появляются ямки травления (рис.5, б), субграни которых сложены поверхностями, параллельными эллиптическому цилиндру. Таким образом легко объясняется «обратная» ориентация ямок травления, боковые поверхности которых отмечены тремя точками на гномонической проекции вокруг рефлекса от грани октаэдра (111). Затем в ходе растворения формируется гранный шов, указывающий на разделение эллиптического цилиндра на два симметричных эллипсоида с углом разориентации — α (рис. 5, в) . Согласно нашим измерениям и данным fi. Л. Орлова [1], в пределе угол достигает 7°. Одновременно вблизи вершин кристалла еще октаэдрического облика появляются фрагменты поверхностей тригон-гексаоктаэдроида, окружающие грань октаэдра. Поверхности додекаэдроида с поверхностями тригонгексаоктаэдрои-да образуют единую поверхность эллипсоида, указанного пунктиром (рис. 5, г). B ходе дальнейшего растворения фрагменты поверхностей додекаэдроида и тригонгексаоктаэдроида становятся все более выпуклыми (рис.5, д), и с исчезновением граней октаэдра и соответственно поверхностей тригонгексаокта-эдроида, остаются только поверхности додекаэдроида с гранным швом, дающие на гномонической проекции характерный треугольный рефлекс (рис. 5, е).

B процессе растворения параметры полуосей эллипсоида, описывающего поверхность кристалла, сближаются,

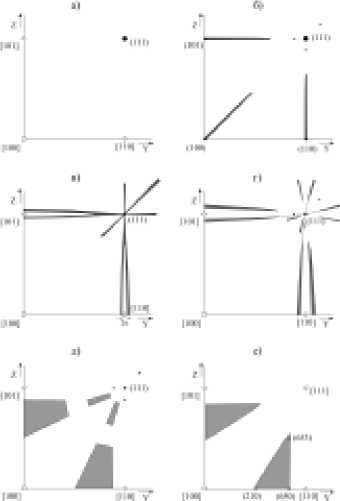
Рис. 5. Процесс растворения кристалла алмаза: а) исходное состояние ‒ идеальный октаэдр, б) начало растворения ‒ формирование эллиптического цилиндра, в) образование «гранного шва», г) начало формирования поверхностей тригонгексаоктаэд-роида, д) развитые выпуклые поверхности додекаэдроида и тригонгексаоктаэдроида, е) предельная форма ‒ додекаэдроид с «гран-ным швом». Обобщенные гномограммы поверхности, первая четверть. Реально присутствующие поверхности отмечены цветом, а символы направлений полыми многоугольниками вместе с тем субграни сохраняющихся ямок травления на реликтовых гранях октаэдра отражают поверхность эллиптического цилиндра, характерного для более ранней стадии процесса. Это объясняется более медленным механизмом диффузионного растворения вещества с поверхностей с нулевой и отрицательной кривизной, отличающимся от механизма «растворения с истиранием» выпуклых поверхностей. Четырехгранные ямки травления на поверхностях округлых кристаллов алмаза, локализующиеся вблизи выхода оси четвертого порядка, также всегда и закономерно образованы поверхностями эллиптического цилиндра. Наиболее симметричный додекаэдроид из исследованной нами выборки бразильских алмазов, подвергшийся длительному растворению, характеризовался следующим набором параметров эллипсоида — 1, 1.23, 1.41, 6.3° .

Необходимо отметить, что даже небольшие явления регенерации кристалла алмаза (рис. 6) практически сразу меняют вид рефлексов от поверхности

в параболическом гониометре — исчезают протяженные световые области и возникают яркие пятна в положении октаэдра (111). Поэтому легко установить признаки регенерации на кристаллах алмаза: кристаллы алмаза любого облика с поверхностями регенерации на экране параболического гониометра дают полярный комплекс идеального октаэдра.

Многочисленные признаки регенерации на округлых кристаллах, установленные нами (см. рис. 6, 7), свидетельствуют о том, что предшествовавшие регенерации процессы растворения и формирование додекаэдроидной формы кристаллами алмаза происходили в области стабильности структуры алмаза, т. е. еще в мантии при высоких температурах и давлениях.

Рис. 6. Регенерация поверхностей алмаза разной длительности: а) кратковременный этап регенерации некристаллографической поверхности алмаза, б) длительный процесс регенерации округлого алмаза

Как правило, после этапа регенерации наступает очередная стадия растворения, и поверхность кристалла алмаза приобретает сложную скульптуру с бугорчатым или шагреневым рельефом, параллельной, занозистой или сноповидной штриховкой. Свидетельством прошедшей регенерации является также плоское дно бывших ямок травления обратнопараллельной ориентации, обнаруживаемых на поверхностях октаэдра. Прямым доказательством значимости процессов регенерации на природных кристаллах алмаза является

Рис. 7. Растворение бугорков регенерации на поверхностях додекаэдроида алмаза хорошо известная форма октаэдрических кристаллов с желобами на месте ребер <110> (рис. 6, б). Такие кристаллы образуются при длительном процессе регенерации кривогранного алмаза, однако не завершившемся восстановлением полного октаэдра.

B течение длительной истории ква-зиравновесного формирования алмаза в верхней мантии (в термодинамической области стабильности структуры алмаза), по-видимому, были возможны флуктуации термодинамических параметров. B твердых кристаллических породах верхней мантии, окружающих алмаз, в первую очередь колебания давления ответственны за переход системы алмаз-флюид через точку равновесия из области пересыщения в область недо-сыщения среды кристаллизации (флюида) по углероду. Колебания давления изменяют в первую очередь активность углерода во флюидной фазе. Широко известно, что растворение кристаллов — процесс несимметричный росту как по морфологическим признакам, так и по кинетике, особенно при больших отклонениях от равновесия. При растворении всегда в первую очередь сглаживаются вершины и ребра кристалла, а сам процесс идет гораздо интенсивнее роста при одинаковых отклонениях от равновесия. Поэтому даже кратковременные этапы растворения алмаза должны оставлять заметный и иногда неустранимый след в морфологии кристалла, находящегося в квази-равновесных условиях.

Активизация тектономагматических процессов в эпоху формирования кимберлитов приводила к наибольшим флуктуациям термодинамических параметров, и прежде всего к скачкам давления в кристаллической верхней мантии. Колебания давления вызывали изменения состава флюидной фазы, меняли прочностные характеристики пород, создавали сдвиговые напряжения и в конечном итоге обуславливали вяз- котекучие движения пород. B такой обстановке кристаллы алмаза, наиболее вероятно, стали растворяться и одновременно вращаться в поле градиента скоростей, приобретая характерные округлые формы с потерей элементов симметрии. B то же время под действием сдвиговых нагрузок в структуре алмаза формировались системы четырех групп плоскостей скольжения {111} (нередко наблюдаемых в окатанных кристаллах), по которым кристаллы чаще всего раскалываются.

Таким образом, кривогранная форма кристаллов алмазов, а именно доде-каэдроид, является динамической неравновесной формой, отражающей трехмерную индикатрису растворения и в небольшой мере истирания гомеополярного кристалла алмаза. Процессы растворения алмазов в природе происходят, вероятно, в динамической обстановке при вращательном движении кристалла и связаны с резкими перепадами давления в эпохи активизации тек-тономагматических процессов, приводящими к нарушениям термодинамического и статического равновесия пород верхней мантии.