Криволинейный пьезоэлектрический актюатор изгибного типа

Цитирование: Паньков А. А. Криволинейный пьезоэлектрический актюатор изгибного типа / А. А. Паньков // Журн. Сиб. федер. ун-та. Техника и технологии, 2025, 18(1). С. 6–18. EDN: HFQHLB

(прогиба). Многослойные гибкие биморфы используют для повышения чувствительности – отношения величины изгибных деформаций биморфа к приложенному на электроды управляющему электрическому напряжению, в частности, когда отражающая поверхность деформируемого зеркала расположена на внешней стороне одного из слоев биморфа [17].

В [34–36] предложены схемы функционирования криволинейных стержневых пьезоэлектрических актюаторов изгибного типа на основе эффекта взаимодействия управляемой трансформации формы, размера [34, 35] или поворота кручения [36] его поперечного сечения и начальной кривизны его продольной оси. Пьезоэлектрическое изменение формы поперечного сечения осуществляется [34, 35] посредством его изгиба в поперечной плоскости; в результате первоначально прямоугольное однослойное, или двухслойное, или кольцевое сечение приобретает «арочный», или двояковыпуклый «чечевичный» [34], или эллиптический [35] вид соответственно. Такие пьезоэлектрические трансформации поперечного сечения приводят к появлению в сечениях криволинейных стержневых актюаторов неуравновешенных изгибающих моментов, действие которых частично распрямляет, т.е. уменьшает значение начальной кривизны продольной оси актюатора. Наиболее существенно этот эффект проявляется при пьезоэлектрической трансформации прямоугольной формы тонкого двухслойного сечения к двояковыпуклой «чечевично»-трубчатой форме [34].

Цель – разработка математической модели, нахождение аналитических решений и изучение эффекта взаимодействия начальной кривизны продольной оси и пьезоэлектрической трансформации размера – высоты поперечных сечений пьезоэлектрических криволинейных стержневых (Curvilinear Rod) CR-актюаторов [35] изгибного типа для улучшения их изгибных характеристик.

Математическая модель актюатора

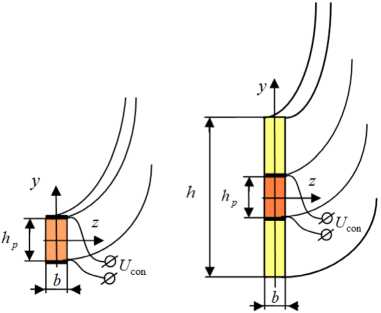
Криволинейный CR-актюатор (рис. 1) представляет собой поляризованный по толщине пьезоэлектрический дугообразный стержень с прямоугольным поперечным сечением и по-

а                       б

Рис. 1. Расчетные схемы криволинейного однослойного (а) и трехслойного (б) пьезоэлектрического актюатора изгибного типа

Fig. 1. Design diagrams of curvilinear single-layer (a) and three-layer (б) bending-type piezoelectric actuator верхностными электродами на его нижней и верхней цилиндрических поверхностях (рис. 1а); возможна установка дополнительных упругих покрытий (слоев) поверх электродов с образованием составного трехслойного CR-актюатора (рис. 1б) для расширения диапазона рабочих характеристик – результирующих значений прогиба и блокирующей силы на свободном торце консоли. При подключении управляющего электрического напряжения Ucon к выходам поверхностных электродов криволинейного CR-актюатора происходит пьезоэлектрическое растяжение или сжатие (в зависимости от знака Ucon) его поперечного сечения по высоте (толщине) на основе обратного пьезоэффекта. Такая пьезоэлектрическая трансформация поперечного сечения обуславливает появление в сечениях криволинейного стержня CR-актюатора реактивных изгибающих моментов. То есть изгиб криволинейного CR-актюатора возникает не от его непосредственного изгиба, как это реализуется по традиционной схеме «биморф», а опосредованно от управляемой пьезоэлектрической трансформации размера его поперечного сечения.

При подключении к электродам управляющего электрического напряжения U _con пьезоэлектрический слой деформируется по толщине на величину

^Sp ⁼ ^222 Л⁰” ,                                                            (1)

hP что обуславливает перемещения

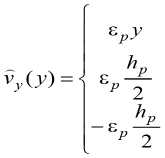
Vye(-^;^)

’      2 2

Vy e (--;--^)

’       2    2

точек составного поперечного сечения (рис. 1), где hp – толщина, d 222 – деформационный пьезомодуль пьезоэлектрического слоя с поляризацией по толщине. С учетом наличия начальной кривизны составного стержня управляемые пьезоэлектрические перемещения V_y (2) обуславливают возникновение удлинений

A(dl) = (Ло + j + vv )dQ - (Ro + y)dQ = vvdQ, осевых деформаций e =AC^Z)=^

* ^zo Ro + У и напряжений

= ^Rx ----                                                        (3)

элементарных «волокон» с начальной длиной dl 0 = ( R 0 + y ) d θ вдоль оси x , где Ex – модуль Юнга по оси x , например, при равенстве значений этого модуля для пьезоэлектрика и для вспомогательных упругих слоев (рис. 1б). В результате в каждом сечении составного (рис. 1) криволинейного стержня (актюатора) возникает результирующий изгибающий момент

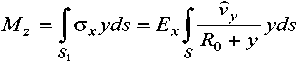
или в виде

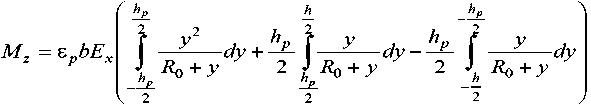
с учетом вида неопределенных интегралов

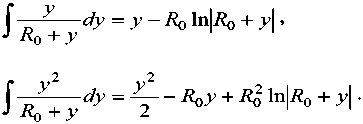
Изгибающий момент Mz (4) частично распрямляет, т.е. уменьшает значение начальной кривизны дугообразной консоли актюатора.

Величины радиальной v • r и окружной v •α компонент

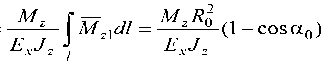
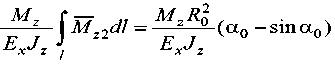
вектора перемещения v • (рис. 2) центра свободного торца дугообразной консоли актюатора определены по методу интегралов Мора c учетом выражений вспомогательных моментов

M_zl = P₁R₀ sin а , М-2 = PtRq (1 — cos а)

от действия единичных сил Д.2 = 1 на свободном торце консоли вдоль радиального и окружного направлений соответственно; при этом величина полного перемещения V. =4^+^ , где Jz – осевой момент инерции составного сечения (рис. 1). Аналогично (5) определим угол поворота

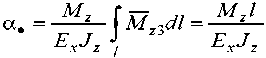
свободного торца консоли с учетом значения вспомогательного моментаЛДз=1, где l = α 0 R 0 – длина консоли.

Величины радиальной P _{• r} и окружной P _•α компонент силы P _• (рис. 2), приложенной в центре свободного торца консоли и блокирующей ее прогиб

Р,г — (Ь^122 Ь2С112)/А, Р.а —(Ь2а11 Ъхах2) / ^

где ^^ — ^11^22 ^12 определим из решения системы линейных алгебраических уравнений

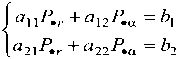
c коэффициентами

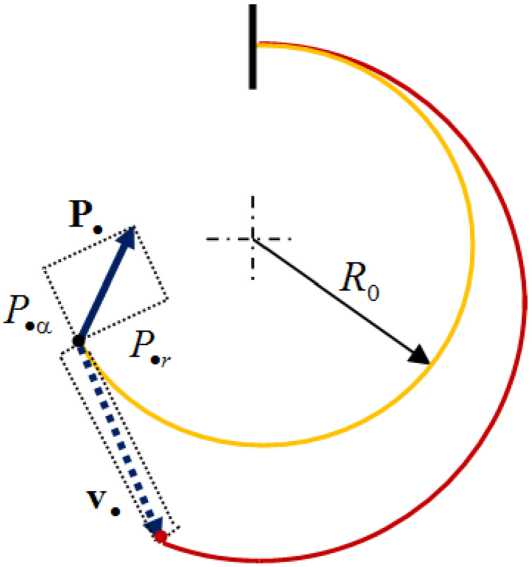
Рис. 2. Начальная и деформированная формы пьезоэлектрического актюатора, где R ₀ – начальный радиус кривизны, P _• – блокирующая сила, v _• – перемещение свободного торца консоли при приложении электрического напряжения U _con

Fig. 2. Initial and deformed shapes of the piezoelectric actuator, where R 0 is an initial radius of curvature, P • is a blocking force, v • is a displacement of the free end of the cantilever when an voltage U con is applied

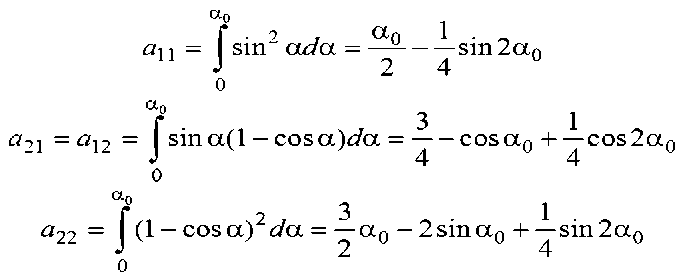
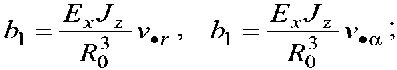
при этом полная величина блокирующего усилия ^» у Р»т + ^«а . Решение (8) получено с ис- пользованием интегралов Мора, представления грузового изгибающего момента MzP в виде разложения

Mzp = [^r Sin а + ^а О “ COS а)К по длине консоли от действия на свободном торце силы P• с компонентами P•r, P•α (рис. 2) и вспомогательных равенств

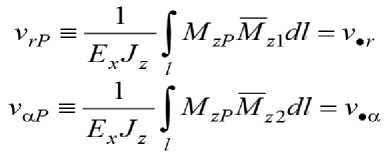
с учетом вида вспомогательных моментов ^^zl , м _z~> (6). Коэффициенты деформационной ζ v и силовой блокирующей ζ _P эффективности

Ц^у.!у. Qp=P./P

криволинейного пьезоэлектрического актюатора (рис. 2) рассчитываем с использованием вспомогательных решений для прогиба и блокирующей силы

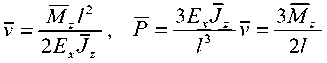
на свободном торце прямолинейной биморфной консоли с поляризацией пьезоэлектрических пластин биморфа по толщине, т.е. по оси y . Решения V , р получены из рассмотрения задач чистого и поперечного изгибов прямолинейного стержня соответственно и могут быть записаны в виде

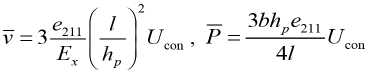
с учетом выражения изгибающего момента

M_z =bh?e_2ll^ = ±bh_pe_2llU_con (11)

как момента пары нормальных пьезоэлектрических сил, действующего в поперечном сечении биморфа, где h ₁ = h_p /2 – толщина каждого слоя – плечо пары сил, J_z =bh*/12 – осевой момент инерции прямоугольного поперечного сечения биморфа. Считаем, что толщина прямолинейного двухслойного биморфа h _bim = h_p (рис. 1), h_p /2 – расстояние и U _con – управляющее электрическое напряжение между взаимодействующими внутренними и наружными поверхностными электродами. Отметим, что решение для прогиба V (10) совпадает с известным решением [37] в приближении e 211 / Ex ≈ d 211 .

Результаты численного моделирования

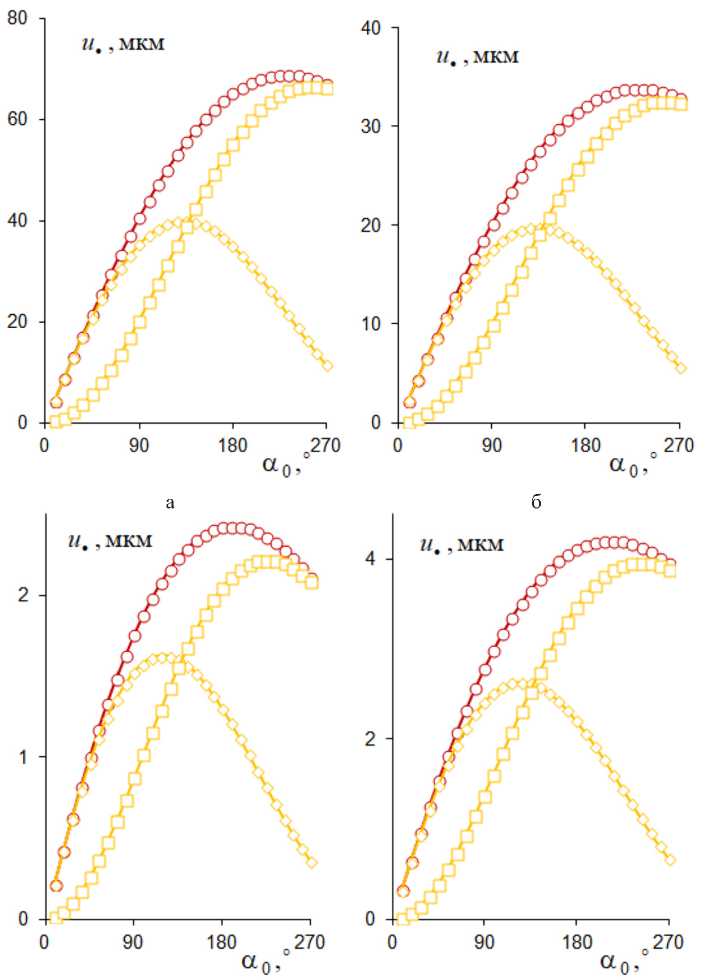
Электроупругие характеристики пьезоэлектрического слоя были заданы через продольный Ex = 61.5 ГПа и поперечный Ey = 53.4 ГПа модули Юнга, пьезомодули d 222 = 373 пКл/Н, e ₂₁₁ = 5.4 Кл/м² керамики PZT-5. Величина приложенного к выходам электродов (рис. 1) управляющего электрического напряжения U con =1500 В. Для составного поперечного сечения (рис. 1б) модуль Юнга вспомогательных верхнего и нижнего упругих слоев приравнен к продольному модулю Ex =61.5 ГПа пьезокерамики. На рис. 3 и 4 в виде графиков представлены результаты расчета зависимостей радиальных u _{• r} , P _{• r} , окружных u _•α, P _•α компонент и абсолютных значений u • , P • векторов перемещения v • (рис. 3) и блокирующей силы P _• (рис. 4) от угла охвата α₀ при фиксированном значении длины l = 100 мм дугообразной консоли (рис. 2) с учетом выражения радиуса R 0 = l /α 0 начальной кривизны ее продольной оси. Ширина поперечного сечения b =5 мм (рис. 1), толщина пьезоэлектрического слоя h_p =1 мм или 2 мм или 20 мм (рис. 1а), а для составного поперечного сечения (рис. 1б) были заданы значения: h_p =2 мм, h =20 мм. Дополнительно на рис. 4в, г приведены значения блокирующей силы p (10) для прямолинейного биморфа с различными значениями 2 мм, 20 мм его толщины h _bim для сравнения со значениями блокирующей силы P _• криволинейного актюатора (рис. 1 и 2).

80 п

60 -

40 -

20 - а и,, мкм и., мкм

б и,, мкм и,, мкм

180      270

а0,

180      270

а0,

180     270

а05

180      270

а0> в                                          г

Рис. 3. Зависимости радиальной u • r (◊) и окружной u •α (□) компонент перемещения u • (○) от угла охвата консоли α 0 при h p = h =1 мм (а), 2 мм (б), 20 мм (в), h p =2 мм, h =20 мм (г)

Fig. 3. Radial u • r (◊) and circumferential u •α (□) components of displacement u • (○) vs cantilever angle α 0 at h p = h = 1 mm (a), 2 mm (б), 20 mm (в), h p = 2 mm, h = 20 mm (г)

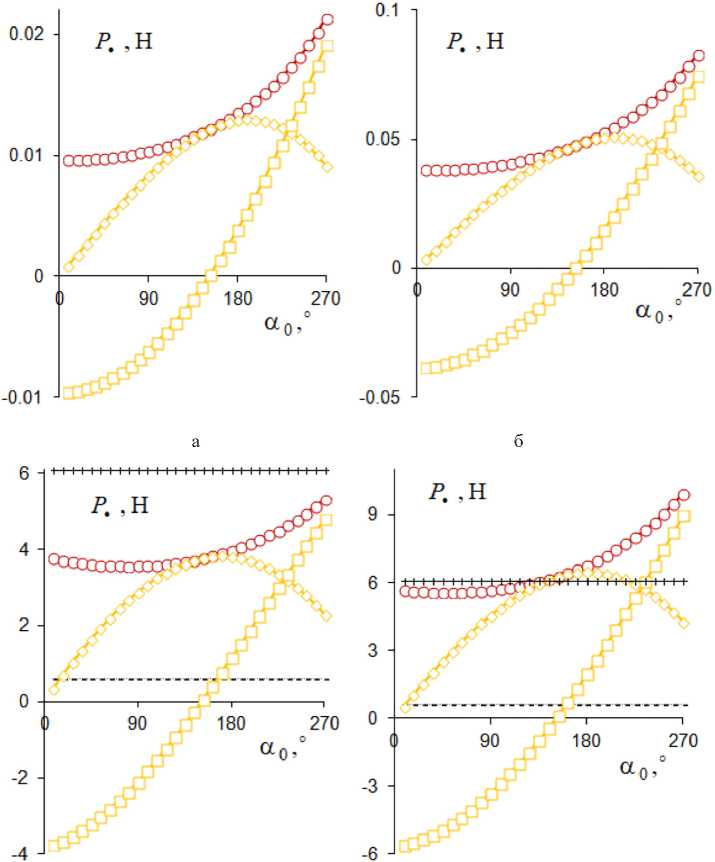
Рис. 4. Зависимости радиальной P • r (◊) и окружной P •α (□) компонент силы P • (○) от угла охвата консоли α 0 при h p = h =1 мм (а), 2 мм (б), 20 мм (в), h p =2 мм, h =20 мм (г) в сравнении со значениями для прямолинейного биморфа толщиной h bim =2 мм (–), 20 мм (+)

Fig. 4. Radial P _{• r} (◊) and circumferential P _•α (□) components of force P _• (○) vs. cantilever angle α₀ at h _p = h = = 1 mm (a), 2 mm (б), 20 mm (в), h _p = 2 mm, h = 20 mm (г) vs. straight-line bimorph at thickness h _bim = 2 mm (–), 20 mm (+)

Выводы

Разработана математическая модель деформирования криволинейного пьезоэлектрического актюатора изгибного типа на основе эффекта взаимодействия двух связанных процессов: активного – управляемого пьезоэлектрического трансформирования – изменения высоты поперечного сечения и реактивного – перехода актюатора к новой равновесной криволинейной форме. Выявлено, что для «простого» (рис. 1а) пьезоэлектрического актюатора в виде однородного пьезоэлектрического дугообразного стержня (рис. 2) имеем рост величины блокирующей – 14 – силы P• с увеличением толщины hp пьезоэлектрического слоя, в частности, от значения ≈0.02 Н при hp =1 мм (рис. 4а) до значения ≈5 Н при hp =20 мм (рис. 4в) при угле обхвата α0 = 270° консоли (рис. 2); при этом величина перемещения u• свободного торца консоли убывает с увеличением толщины hp пьезоэлектрического слоя (рис. 3). Имеем немонотонную зависимость величины перемещения u• (рис. 3) и практически монотонно возрастающую зависимость величины блокирующей силы P• (рис. 4) от угла обхвата α0 консоли в исследуемом диапазоне значений (0°; 270°). Из сравнения характеристик u• (рис. 3в, г), P• (рис. 4в, г) подобных пьезоэлектрических криволинейных актюаторов с простым (рис. 1а) и составным (рис. 1б) поперечными сечениями одинаковой 20 мм толщины установлено, что наличие дополнительных слоев в составном сечении (рис. 1б) приводит к увеличению значений обеих характеристик u•, P•, что обусловлено более высокими (по сравнению с простым сечением на рис. 1а) значениями напряженности электрического поля из-за меньшего расстояния между электродами пьезоэлектрического слоя при одинаковом значении управляющего электрического напряжения Ucon. Установлено (рис. 4г), что для случая составного (рис. 1б) поперечного сечения и значений угла α0 > 135° величина блокирующей силы P• для криволинейного актюатора превышает соответствующее значение силы p (10) для прямолинейного биморфного актюатора при толщине биморфа hbim = hp (рис. 1), расстоянии hp/2 между внутренним и наружными электродами и управляющем электрическом напряжении Ucon.