Кривые течения и деформирования нелинейной модели сдвигового течения тиксотропных вязкоупругопластичных сред, учитывающей эволюцию структуры
Автор: Хохлов А.В., Гулин В.В.
Статья в выпуске: 1, 2024 года.
Бесплатный доступ
Продолжено системное аналитическое исследование математических свойств нелинейной модели сдвигового течения тиксотропных вязкоупругопластичных сред, учитывающей взаимовлияние процесса деформирования и эволюции структуры (кинетики образования и разрушения межмолекулярных связей и ассоциатов макромолекул), предложенной ранее. При произвольных шести материальных параметрах и (возрастающей) материальной функции, управляющих моделью, аналитически изучен фазовый портрет системы двух нелинейных дифференциальных уравнений для безразмерных напряжения и степени структурированности, к которой сведена модель, в окрестности ее единственного положения равновесия, и базовые свойства кривых течения и кривых деформирования с постоянной скоростью сдвига, порождаемых моделью. Тем самым начат анализ способности модели описывать поведение как жидкообразных сред, так и твердообразных (густеющих, твердеющих, затвердевших) вязкоупругопластичных сред: эффекты скоростного и деформационного упрочнения, релаксации, ползучести, восстановления и др. Исследованы характер зависимости кривых деформирования от деформации сдвига (монотонность, выпуклость, мгновенный модуль, эволюция касательного модуля), от скорости сдвига и начальной структурированности и от материальных параметров и функции модели (в частности, параметров, управляющих влиянием структурированности на вязкость и модуль сдвига и влиянием напряжения на скорость разрушения структуры). Доказано, что кривые деформирования могут быть как возрастающими, так и иметь участки убывания, напоминающие «зуб текучести», и затухающие осцилляции, что все кривые деформирования имеют горизонтальные асимптоты (напряжение установившегося течения), монотонно зависящие от скорости сдвига, и напряжение течения строго возрастает с ростом скорости, что их мгновенный модуль сдвига, наоборот, зависит от начальной структурированности, но не зависит от скорости. При определенных ограничениях на материальные параметры модель способна обеспечить и билинейную форму кривых деформирования, свойственную идеальной упругопластичной модели, но со скоростной чувствительностью. Установлено, что семейство кривых деформирования не обязано быть возрастающим ни по начальной структурированности, ни по скорости сдвига: в некотором диапазоне скоростей сдвига, в котором положение равновесия является «зрелым» фокусом и наблюдаются выраженные осцилляции кривых деформирования, возможно переплетение кривых деформирования с разными скоростями сдвига. Исследовано, как меняется структурированность в процессе деформирования в зависимости от материальных параметров и функции модели, скорости сдвига и напряжения. Начальная структурированность влияет лишь на начальный участок кривых деформирования, но не влияет на их асимптоты и на установившуюся величину структурированности, которая монотонно убывает с ростом скорости сдвига. Разнообразие типов поведения структурированности во времени (в частности, обнаруженное резкое обрушение структуры при достижении критических величин напряжения) порождает ряд необычных эффектов (непривычных свойств) по сравнению с типичными кривыми деформирования структурно стабильных материалов.
Тиксотропия, вязкоупругопластичность, реология, полимерные системы, сдвиговое течение, скорость сдвига, степень сшитости, интегральные кривые, положение равновесия, фазовый портрет, устойчивый фокус, кривая течения, диаграммы деформирования, напряжение течения, скоростная чувствительность, сверхпластичность, индикаторы применимости
Короткий адрес: https://sciup.org/146282819
IDR: 146282819 | УДК: 539.3 | DOI: 10.15593/perm.mech/2024.1.10
Flow curves and stress-strain curves generated by a nonlinear model for shear flow of thixotropic viscoelastic media accounting for structure evolution
A systematic analytical study of the mathematical properties of the nonlinear shear flow model of thixotropic viscoelastic-plastic media is continued. It takes into account the mutual influence of а deformation process and structure evolution (the kinetics of the formation and destruction of intermolecular bonds and associates of macromolecules). The model is reduced to the system of two nonlinear differential equations for the dimensionless stress and the degree of structuredness (i.e. cross-links density and so on). Assuming six material parameters and an (increasing) material function governing the model are arbitrary, the phase portrait of the system is analytically studied in the vicinity of its single equilibrium point. Basic properties of flow curves and stress-strain curves with constant shear rate generated by the model are examined. Thus, the analysis of the model ability to describe the behavior of both liquid-like media and solid-like (thickening, hardening, solidifying) viscoelastic-plastic media has been started: the effects of strain-rate and strain hardening, relaxation, creep, recovery, etc. The stress-strain curves dependence on the shear deformation (monotonicity, convexity, instantaneous modulus, tangent modulus evolution), on the shear rate and initial structuredness and on the material parameters and function of the model (in particular, the parameters that control the effect of structuredness on viscosity and shear modulus and the influence stress on the rate of destruction of the structure) has been studied. It is proved that stress-strain curves can be both increasing and have sections of decrease, resembling a yield-drop, and damped oscillations; that all stress-strain curves have horizontal asymptotes (steady flow stress), monotonically dependent on shear rate, and the flow stress strictly increases with increasing shear rate; that their instantaneous shear modulus, on the contrary, depends on the initial structuredness, but does not depend on shear rate. Under certain restrictions on the material parameters, the model is also capable to provide a bilinear form of stress-strain curves, which is intrinsic for an ideal elastoplastic model, but with strain rate sensitivity. It has been established that the family of stress-strain curves does not have to be increasing function of initial structuredness or shear rate: in a certain range of shear rates, in which the equilibrium point is a “mature” focus and pronounced oscillations of stress-strain curves are observed, it is possible that stress-strain curves with different shear rates may interweave with each other. It is studied how structuredness changes in the process of deformation depending on shear rate, stress, material parameters and material function of the model. The initial structuredness affects only the initial arc of stress-strain curves, but does not affect their asymptotes and the steady value of the structuredness, which monotonically decreases with increasing shear rate. A variety of scenarios of structuredness behavior over time (in particular, the observed sharp collapse of the structuredness when critical stress values are reached) generates a number of unusual effects (unusual properties) in comparison with typical properties stress-strain curves of structurally stable materials.
Текст научной статьи Кривые течения и деформирования нелинейной модели сдвигового течения тиксотропных вязкоупругопластичных сред, учитывающей эволюцию структуры
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2024PNRPU MECHANICS BULLETIN
Эта статья - прямое продолжение исследований [1; 2], посвященных формулировке одноосного прототипа нелинейного определяющего соотношения (ОС) для изотермического сдвигового течения тиксотропных вязкоупругопластичных сред, учитывающего взаимное влияние процессов деформирования и эволюции структуры (кинетики образования и разрушения межмолекулярных связей и ассоциатов макромолекул), его сведению к системе двух нелинейных дифференциальных уравнений s = aeew - se(в-а)w, (1)
w = c [(1 - w (1 + bg ( s ))] (2)
для безразмерных касательного напряжения s ( t ) и степени структурированности w ( t ) ( t - безразмерное время) и аналитическому исследованию ее положения равновесия и фазового портрета в зависимости от всех пяти безразмерных материальных параметров (МП) a , b , c , а > 0 , в > 0 (см. ниже), постоянной скорости сдвига v (она входит в безразмерный параметр a = v n0 /т c ) и произвольной неубывающей кусочно-гладкой материальной функции (МФ) g ( s ), описывающей зависимость скорости разрушения сшивок от напряжения (см. (5)).
Адекватное описание нелинейных реологических эффектов, построение ОС течения неньютоновских вязких жидкостей и вязкоупругопластичных сред
(например, суспензий, гелей, полимеров в вязкотекучем состоянии или в виде расплавов и растворов, битумов и их модификаций минеральными и эластомерными наполнителями, C-SiC паст для 3D-печати заготовок, металлов и сплавов в сверхпластичном состоянии и т.п.) важно для понимания закономерностей и моделирования огромного количества природных и технологических процессов [3–48]: движения магмы, поведения грунтов, схода селей и лавин, разнообразных технологий переработки полимеров и других материалов (экструзии волокон, прессования, сверхпластической штамповки и т.п.), нефтедобычи (в частности, методом гидроразрыва пласта) и перекачки нефти, дорожного строительства, производства лаков, красок, масел, пищевых продуктов, медицинской микрофлюидики и т.п.
Стационарное течение жидких сред при фиксированной температуре принято описывать кривой течения или кривой вязкости (графиками зависимости напряжения и кажущейся вязкости от скорости сдвига). Базовые наблюдаемые у неньютоновских жидкостей реологические эффекты – зависимость вязкости среды от скорости сдвига («аномалия вязкости»), температуры и давления [3–48], тиксотропия (явление обратимого изотермического уменьшения вязкости при увеличении скорости сдвига и ее восстановления при уменьшении скорости) [10–27; 32; 38–43], существование конечного предела вязкости при стремлении скорости к нулю или к бесконечности (максимальной и минимальной Ньютоновых вязкостей) [5–27; 29–33; 38–43; 47; 48], сверханомалия вязкости (наличие участка убывания на кривой течения) [34–38], разбухание экструдата при выходе из канала фильеры (эффект Баруса) [10–27; 38–43] и др. Обычно для аппроксимации кривой течения среды используют простейший степенной закон. Поскольку такая зависимость не распространяется на весь диапазон скоростей сдвига, а начальная вязкость равна бесконечности (для псевдо-пластичных жидкостей) или нулю (для дилатантных), то за полтора столетия, начиная с работ Максвелла, Шведова, Бингама, Оствальда, Ребиндера и др., предложено более сотни разных эмпирических и полуэмпирических определяющих соотношений (реологических моделей), аппроксимирующих нелинейные зависимости напряжения (или вязкости) от скорости сдвига разных сред в определенном интервале скоростей сдвига (модели Шведова – Бингама, Гершеля – Балкли, Кэссона, Кросса, Кригера, Джиллеспи, Бернштейна – Кирсли – Запаса (BKZ), Олдройда, Леонова – Прокунина, Карро – Ясуда, Виноградова – Покровского, Гиезекуса, Менцера, Фан-Тьен – Тэннера и др.) [5–33; 38–48], реология стала самостоятельным разделом науки на стыке физики, химии, механики, материаловедения. Большинство моделей носят феноменологический характер, содержат подгоночные параметры, не имеющие физического смысла, не учитывают упругость жидких сред и эволюцию их микроструктуры (образование и разрушение кристаллитов и агрегатов, Ван-дер-Ваальсовых связей между молекулами, сшивок и т.п.).
Представления о том, что понижение вязкости с увеличением скорости сдвига обусловлено постепенными структурными изменениями полимерной системы, развивались, начиная с первых работ, в которых был описан этот эффект. Уже В. Оствальд (в 1926 г.) обнаружил, что вязкость, определяемая отношением напряжения к градиенту скорости сдвига, зависит от режима деформирования. Он назвал эту вязкость «структурной вязкостью», а сам эффект – «аномалией вязкости». В полимерных системах (расплавах, концентрированных растворах и т.п.) наличие структуры (разнообразных связей между макромолекулами и надмолекулярными агрегатами) обусловлено, прежде всего, огромной длиной и сложной формой макромолекул, их гибкостью, многочисленными степенями свободы их сегментов, наличием межмолекулярных взаимодействий, приводящих к образованию (и разрушению) зацеплений, узлов, водородных связей, сшивок, кристаллитов и других элементов сложной пространственной (сетчатой) структуры, эволюция которой влияет на механические свойства [10–15; 19–27; 31– 43; 47; 48].
Лишь немногие из сотни известных ОС жидких сред учитывают не только их вязкость и пластичность, но и вязкоупругость (столь характерную, например, для расплавов и концентрированных растворов полимеров, для жидкостей-пропантоносителей и т.п.) и – так или иначе – эволюцию структуры [7; 10–15; 19–27; 32–43; 47; 48]; последняя в большинстве случаев описывается всего одним структурным параметром. Приложению сформулированного ОС к описанию конкретных экспериментальных данных и численному решению краевых задач практически никогда не предшествует системное аналитическое исследование математических следствий из ОС для произвольных МП и МФ, управляющих им, анализ, позволяющий строго математически описать круг реологических эффектов, которые ОС может или не может моделировать, найти область применимости и индикаторы применимости ОС, которые удобно проверять по данным испытаний (как это сделано в серии статей автора, посвященных качественному анализу ряда линейных и нелинейных ОС вязкоупругопластичности [49–57]). Несмотря на очевидное значение этого вопроса для химии и технологии полимеров, он изучен недостаточно. Учитывается в лучшем случае влияние изменения структуры на характер течения, но не учитывается влияние деформирования на кинетику изменения структуры. Отсутствие учета взаимного влияния эволюции структуры и процесса деформирования и системного качественного анализа ОС не позволяет развить достаточно детальную и адекватную методику обработки данных реометриче-ских испытаний сложных жидкостей (текучих систем) и теорию процессов переработки материалов с учетом влияния всех важных для процессов факторов, проанализировать влияние этих факторов и выбрать важнейшие из них в разных режимах деформирования. Представляется принципиально важным адекватно описывать и моделировать эволюцию структуры, конкуренцию и взаи- мосвязанность процессов, влияние напряжения и его истории на текущую скорость трансформации структуры.
Данная статья - продолжение исследований [1; 2], в которых предложена модель для описания изотермического сдвигового течения тиксотропных вязкоупругопластичных сред, учитывающая взаимное влияние процессов деформирования и эволюции структуры (см. п.1), осуществлено ее сведение к системе двух нелинейных дифференциальных уравнений (1), (2) для касательного напряжения 5 ( t ) и степени структурированности w ( t ), и начато аналитическое исследование ее положения равновесия и фазового портрета в зависимости от скорости сдвига, всех шести МП и МФ g ( 5 ), которыми управляется модель. Для произвольных МП и МФ в [1; 2] доказана единственность положения равновесия этой системы, в общем виде исследованы зависимости его координат от всех МП и от скорости сдвига, доказано, что все зависимости монотонны. Выведены и исследованы уравнения кривой течения и кривой вязкости, доказано, что модель приводит к возрастающей зависимости равновесного напряжения от скорости сдвига и к убывающей кривой кажущейся вязкости, отражающим типичные свойства экспериментальных кривых течения псевдопласти-ческих сред, но не способна описывать сверханомалию вязкости (наличие участка убывания у кривой течения). Доказано, что положение равновесия всегда устойчиво и возможны ровно три случая: точка равновесия - устойчивый узел или вырожденный узел, или устойчивый фокус. Найдены критерии реализации каждого случая в виде явных ограничений на МФ и МП модели и скорость сдвига.
Основные задачи данной статьи - продолжение системного аналитического исследования общих свойств модели (1), (2) при произвольных МП и МФ: изучение интегральных кривых и фазового портрета в окрестности единственного положения равновесия нелинейной автономной системы (1), (2), исследование свойств кривых течения и семейства диаграмм деформирования (ДД) с постоянной скоростью сдвига, порождаемых моделью, особенностей эволюции структуры в зависимости от МП и МФ и способности модели описывать поведение как жидкообразной, так и твердообразной (густеющей, твердеющей, затвердевшей) тиксотропных вязкоупругопластичных сред: типичные свойства ДД, эффекты скоростного и деформационного упрочнения, релаксации, ползучести, восстановления и др.
-
1. Модель сдвигового течения тиксотропных сред, учитывающая взаимное влияние эволюции структуры и процесса деформирования
Примем для описания изотермического сдвигового деформирования полимеров в вязкотекучем состоянии и в виде расплавов и концентрированных растворов и гелей нелинейную модель Максвелла
Y = т / G + т / п , (3)
в которой т - касательное напряжение, Y - скорость сдвига, а материальные параметры зависят от изменения структуры полимера под влиянием деформирования: будем считать, что модуль сдвига G и динамическая вязкость ] зависят от одного безразмерного структурного параметра w ( t ). Скорость (простого) сдвига Y = V (в этой работе) будем считать постоянной (заданным кинематическим параметром), а за w ( t ) примем степень «сшито-сти» полимера w , т.е. отношение концентрации надмолекулярных или межмолекулярных связей (зацеплений, водородных связей, химических сшивок и т.п.) в текущий момент времени к некоторому максимально возможному значению концентрации связей для данной температуры: G = G ( w ), П = П ( w ), w ( t ) е [0;1], w (0) = w 0 , w 0 е [0;1). На данном этапе будем характеризовать текущую структуру полимера только одним структурным параметром w ( t ), не различая механизмы влияния разных элементов (над)молекулярной структуры на вязкость; пока будет важно лишь то, что материал имеет структуру, которая разрушается под действием сдвиговых напряжений и может восстанавливаться. В дальнейшем модель будет обобщена введением второго структурного параметра, учитывающего механизм ориентирования и распрямления макромолекул (гибкоцепных) полимеров при одноосном деформировании.
Вообще говоря, модуль сдвига G и динамическая вязкость п зависят не только от w (и других структурных параметров), но и от температуры, давления и скорости сдвига v (градиента скорости или напряжения т), однако температуру, давление и скорость сдвига мы пока считаем постоянными (рассматриваем изотермический процесс и сдвиговое течение с постоянной скоростью v). Величины G = G ( w ) и п = п ( w ) должны быть возрастающими функциями от степени сшитости, поэтому можно принять, что
П(w) = п0eаw, G(w) = G0eew, где п0,G0 >0, 0
(следуя традициям кинетики выберем эти функции экспоненциальными). Поскольку вязкость обычно сильнее зависит от степени сшитости (и от температуры), чем модуль сдвига, то p < а (и можно положить р = 0, чтобы пренебречь зависимостью модуля сдвига от w), и потому время релаксации модели Максвелла (3) T = п / G выражается формулой T(w) = T0e<и-в)w, T0 =п0/G0, и возрастает с ростом w. Материальные параметры (МП) G0 и п0 в (4) характеризуют минимальные модуль сдвига и динамическую вязкость при w = 0 , а также в начальный момент (при t = 0), когда w(0) = w0 (относительную концентрацию сшивок в начальный момент времени w0 е [0;1] можно рассматривать как дополнительный МП модели).
Таким образом, в уравнение (3) входят две неизвестные функции времени т( t ) и w ( t ), и необходимо добавить некоторое кинетическое уравнение, описывающее эволюцию степени сшитости полимера во времени с учетом влияния напряжения (процесса деформирования).
Изменение числа сшивок в ходе деформирования происходит в результате наложения двух конкурирующих процессов: разрушения имеющихся сшивок и образования новых. При увеличении напряжения разрушение (т.е. убывание w(t)) ускоряется (соответственно вязкость падает), а скорость образования новых сшивок можем считать постоянной (при фиксированной температуре) и пропорциональной плотности вакансий (1-w). Поэтому кинетическое уравнение для степени сшитости можно принять в виде w = ki(1 - w) - k 2 g (s) w, (5)
где k 1 , k 2 > 0 - МП (вообще говоря, зависящие от температуры), задающие скорости образования и разрушения сшивок (их размерность - с-1), g ( s ), s - 0, - неотрицательная неубывающая МФ, такая что g (0) = 1 и g ( +^ ) = +^ , задающая зависимость скорости разрушения сшивок от безразмерного напряжения s = т ( t )/т c ( Т c - некоторое характерное касательное напряжение: пороговое, предельное или просто Т c = G 0 или Т c = G 0 /100).
Таким образом, в модели (3)-(5) (управляемой шестью МП, k 1, k 2, n0, G 0, а > 0, в - 0, и одной МФ g ( s )) учитывается кинетика взаимосвязанного протекания двух процессов: сдвигового течения и структурных изменений в материале. В уравнении (3) вязкость и модуль упругости зависят от структурного параметра (характеристика второго процесса), а скорости разрушения и восстановления структуры зависят от напряжения (характеристики первого процесса).
Введем безразмерное время t = t/T0, где T0 = П0/G0 -минимальное время релаксации модели Максвелла (при w = 0 ), и заменим аргумент в искомых функциях s(t) и w(t) системы (3), (5) по формулам Y(t) = y(T0t), Y'(t) = T0y(T01). Тогда после упрощения обозначений (замены t на t, штриха на точку в обозначении дифференцирования, прописных букв S, W в обозначении функций от t - на строчные) получим уравнения модели (3)-(5) в безразмерном виде (1), (2). Это автономная система нелинейных дифференциальных уравнений для s(t) и w(t), t - безразмерное время, a = vn0/Tc = VT0G0/tc - безразмерный параметр, зависящий от скорости сдвига v и вязкости п0 (или T0), b = k2/k1 и c = k1 T0 - безразмерные МП, характеризующие борьбу процессов образования и разрушения сшивок и соотношение их скоростей с временем релаксации T0. К ней надо добавить начальные условия w(0) = w0 и s(0) = s0. Система (1), (2) удовлетворяет условиям теоремы существования и единственности решений задачи Коши, если МФ g(s) непрерывно дифференцируема при s > 0 .
2. Родственное нелинейное ОС вязкоупругопластичности типа Максвелла
Изучаемая модель (1)-(3) родственна физически нелинейному ОС типа Максвелла s,(t) = f е(tMt)-1[o,(t)-a0(t)Sj] + 39(t)S, , (6)
e( t ) = M o = E - 1 F (o( t )) + n - 1 j V (о(т)) d т ,
t
0( t ) = M 0 ^ 0 = E 0 - 1 F (0 0 ( t )) + П 0 1 j V 0 (o (т)) d T, 0
с четырьмя возрастающими МФ F ( x ), V ( x ), F0 ( x ), V 0( x ) и МП E , n, E 0, n0 > 0, исследованному в цикле статей [49-55] (и др.). Оно связывает истории изменения тензоров деформаций е ( t ) и напряжений о ( t ) в точке тела в предположении отсутствия взаимного влияния шаровых и девиаторных частей тензоров e = е - е0 1 и s = о - o0 I (независимости объемной деформации 9( t ) от касательных напряжений и интенсивности напряжений o = (I s , s , ) 0'5 , а деформаций сдвига и интенсивности деформаций е = ( 3 e i^, ) 0'5 - от среднего напряжения o0( t )) и пренебрегая влиянием третьих инвариантов тензоров. Одномерный прототип ОС (6) получается из классической модели Максвелла заменой линейных упругого и вязкого элемента на нелинейные, управляемые МФ F ( x ) и V ( x ) соответственно, т.е. опирается на разложение полной деформации в сумму упругой и вязкопластической компонент.
ОС (6) обобщает (включает) классические степенные модели вязкого течения и ползучести, реологические модели Гершеля - Балкли и Шведова - Бингама и частные случаи моделей Соколовского - Малверна и VBO (обзор и библиографию по этим темам см. в работах [50; 51; 53; 54]). Нелинейные интегральные операторы M и М0 управляют процессами формоизменения и развития объемной деформации (не влияющими друг на друга). Модули упругости E , E0 и коэффициенты вязкости n, По выделены из МФ для удобства учета влияния температуры в форме E = E (T), n = n(T), E 0 = Eо( T), По = n0(T) [51] и обезразмеривания времени с помощью параметра тr = n / E • В столь общей форме ОС (6) исследованию еще не подвергалось до статей [49-55]. В них доказано, что ОС (6) (при определенных ограничениях на несколько своих МФ) хорошо описывает более десятка базовых эффектов (см. список в [50; 51; 53; 54]), типичных для вязкоупругопластических твердых тел (а не только для жидких вязкоупругих сред), в частности, пригодно для описаний кривых нагружения и разгрузки, циклического нагружения, рэтчетинга, различных эффектов при ползучести и сверхпластическом деформировании. Обнаруженные в [49-55] свойства и возможности этого ОС служат ориентирами для дальнейшего исследования свойств модели (3)-(5) (в частности, семейств кривых деформирования, релаксации и ползучести, которые она порождает) и ее обобщений для расширения круга описываемых эффектов.
3. Существование и единственность точки равновесия системы (1), (2)и ее зависимость от МП
Положения равновесия системы (1), (2) - решения системы уравнений
5 = ае а w , w = F ( 5 ), (7)
где F(5) := (1 + bg(5)) 1, 5 > 0 ■ Они зависят лишь от трех параметров а , a = vn0/Tc и b = k2/k1 и МФ g (и не зависят от параметров c, G0 , в из (2) и (4)). Функция F(5) -убывающая функция с множеством значений (0;(1 + b)-1], F(5) ^ 0 при 5 ^~ в силу ограничения g(+^) = +^ ■ Так как из первого уравнения w = а 1 ln 5/а - возрастающая функция 5 при 5 > 0, а второе уравнение (7) задает убывающую функцию w(5) (для любой возрастающей МФ g(5)), то система (7) имеет не более одного решения. Решение ровно одно (существует), поскольку область значений непрерывной функции а-1 ln 5/а , 5 > а, совпадает с полуосью [0, +^) . Обозначим точку равновесия (равновесные напряжение и степень сшитости) через (5., w.), 5. = 5.(а,b,а), w. = w.(а, b, а). Из (7) следуют уравнения для определе ния 5. и w. :
ln 5 . / а = а F ( 5 . ); (8)
w . = F ( 5 . ) (9)
Очевидно, при любых МП и МФ 5. > а > 0, w. е (0;1). В силу (9) кривая w = F(5) в фазовом пространстве {(w, 5)| wе [0;1], 5 > 0} системы уравнений (1), (2) - геометрическое место точек равновесия; она не зависит от параметра а, т.е. от скорости сдвига, и с изменением а, точка равновесия двигается вдоль нее. Кроме того, кривая w = F(5) - множество точек, в которых поле скоростей системы уравнений (1), (2) горизонтально, т.е. структурированность w(t) имеет локальный экстремум (w = 0 ) в точках пересечения любой фазовой кривой с кривой w = F (5). В работе [1] доказаны следу -ющие утверждения о зависимости точки равновесия (5., w.) от МП.
ТЕОРЕМА 1 . Пусть а , b , а , c , n 0, G 0 > 0, в > 0 и МФ g ( 5 ) непрерывна и кусочно дифференцируема при 5 > 0, не убывает и g (0) = 1. Тогда система двух нелинейных дифференциальных уравнений (1), (2) имеет единственное положение равновесия ( 5 . , w . ) в области w е (0;1), 5 > 0, оно является решением системы уравнений (8), (9), зависит лишь от трех параметров а , а = vn 0/ T c и b = k 2 / k 1 (и не зависит от c , в , G 0), а функции 5 . ( а , b , а ) и w . ( а , b , а ), а , b , а> 0, обладают следующими свойствами:
-
1) 5 . > а > 0, пределы при а ^+ 0 и а ^^ (т.е. при v^ 0 и v^^ ): 5 . (0 + ) = 0, w . (0+) = (1 + b )-1 и 5 . ( +^ ) = +^ ; 5 . ( а ) / а ^ 1 при а ^ ~ и w . ( +^ ) = 0, если g ( +^ ) = +^ ;
-
2) функции 5 . ( а , b , а ) и w . ( а , b , а ) монотонны по каждому из аргументов в области а , b , а > 0 ;
-
3) 5 . и w . монотонно убывают по b , производная 5 . b = -а 5 . g ( 5 . ) w »2[1 + а bw . 5 . g '( 5 . )]-1< 0 ;
-
4) функция 5 . ( а , b , а ) возрастает по а при а > 0, а степень сшитости (9) убывает по а
- 5.а / 5. = w.[1 + аbw.2 5. g'(5.)] 1 > 0 ,
w -а =- F ( 5 . )2 bg ‘( 5 ♦ ) 5 -а =- bw2 g ‘( 5 ♦ ) 5 -а , (10)
sgn w . а =- sgn 5 . а , 0 < 5 . а / 5 . < w . < 1;
-
5) равновесное напряжение 5 . ( а , b , а ) - возрастающая функция параметра а (и скорости сдвига v, и МП П 0) на интервале а > 0, а равновесная степень сшитости (9) убывает по а и v , производные 5 . и w . по а (обозначаем их штрихом) выражаются формулами
5 ‘ = 5 . а 1 [1 + а b5 . F ( 5 , )2 g '( 5 . )] 1 > 5 . а 1 , w ‘ = - bw . 2 g '( 5 . ) 5' ,
Возрастание реологической кривой 5 . ( а ) - важнейшее качественное свойство типичных кривых вязкости, наблюдаемых для разных псевдопластичных жидкостей [5-32].
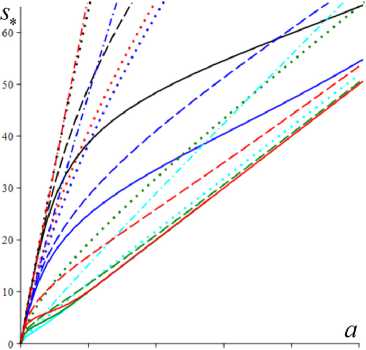
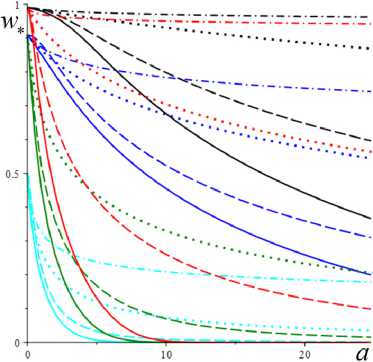
На рис. 1, а , b , приведены графики 5 . ( а ) и w . ( а ) (зависимостей от скорости сдвига) для МФ
g ( s ) = e h , g ( s ) = 1 + ( hs )2, g ( s ) = 1 + hs , g = 1 + ln(1 + hs )
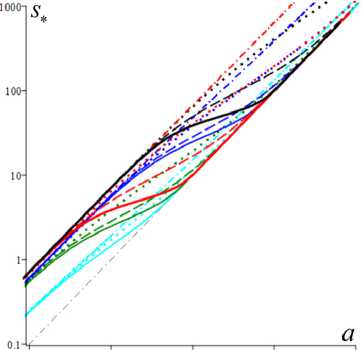
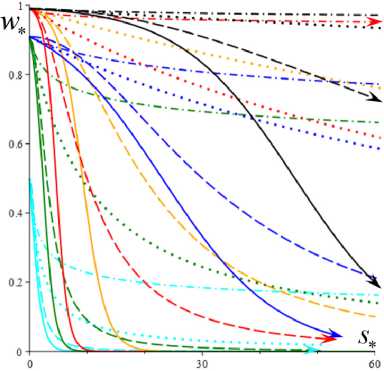
(сплошные, штриховые, пунктирные или штрихпунктир-ные линии для каждой МФ) и пяти наборов МП с фиксированными a = 2, в = 1 и с разными парами b и h: b = 0.01, h = 0.1 (черным цветом), b = 0.01, h = 1 (красным), b = 0.1, h = 0.1 (синим), b = 0.1, h = 1 (зеленым) и b = 1, h = 1 (голубым). Увеличение каждого из параметров b и h приводит к смещению кривых s* (a) и w* (a) вниз. На кривых s* (a) всех моделей есть точки перегиба (выпуклость вверх сменяется выпуклостью вниз), и это отражает типичное поведение экспериментальных кривых течения неньютоновых сред. Для любых МФ и МП при а ^ 0 s*(a) ^ 0, s* (a) ^ ea/(1+b), и w* ^ (1 + b)-1, а при a ^ ~ s./a ^ 1, w. ^ 0 , и кривые течения s.(a) для всех МФ (12) обладают наклонной асимптотой, параллельной прямой s = a (и лежат выше асимптоты). Для моделей с МФ g = 1 + (hs)2 или g = ehs (и любым h > 0) асимптота общая: s = 1 • a (см. сплошные и штриховые кривые на рис. 1, а). А вот для линейных МФ g = 1 + hs асимптоты кривых s.(a) (см. пунктирные линии) имеют вид s = a + B , где B = a / (bh). Поэтому на всех кривых рис. 1 есть точки перегиба при достаточно больших a. На рис. 1, c, приведены те же кривые течения s* (a), что и на рис. 1, а, но в логарифмических координатах (как принято в реологии), с охватом более широкого диапазона скоростей сдвига. На рис. 1, d, приведены кривые {s.(a), w.(a) | a е [0;50)} в фазовом пространстве для тех же МФ (12) и пяти наборов МП что и на рис. 1, а–c, и для b = 0,01, h = 0.5 (желтые кривые). Все кривые при a ^ ~ стремятся к асимптоте w. = 0 (ибо s. (^) = ^, w. (^) = 0), но с разными скоростями; s.(a) растет тем медленнее, чем быстрее растет МФ g(s). Самый быстрый рост s*(a) и самое медленное убывание w* (a) – у моделей с логарифмической МФ (штрихпунктирные кривые). Все кривые на рис. 1, d, оборваны при a = 50 или s. = 60, стрелками указано направление возрастания параметра а.
О 10 20 30 40 50
a
b
с
d
Рис. 1. Зависимости положения равновесия от скорости сдвига (параметра a ) и кривые течения s * ( a ) в логарифмических координатах, порождаемые моделями с разными МП и МФ (12)
Fig. 1. Dependences of the equilibrium position on the shear rate (parameter a ), and flow curves s * ( a ) , in logarithmic scale, generated by models with different material parameters and functions (12)
4. Зависимость кажущейся вязкостиот скорости сдвига и МП модели
Из (8) следует зависимость (установившейся) кажущейся вязкости μ : =τ */ ν=η 0 s */ a от равновесного напряжения s * =τ */ τ c (а также от скорости сдвига ν или степени сшитости w * ), порождаемая построенной моделью (с любыми МП a , b , α , c , η 0, G 0 > 0, β ≥ 0 и любой неубывающей МФ g ( s ) ≥ 1) при рассматриваемом режиме деформирования:
μ=η0exp(α[1+ bg ( s *)]-1), или μ=η( w *)=η0 e α w * (13)
(формулу (13) можно получить и подстановкой w = w * в (4)). При фиксированной скорости сдвига, когда меняются только параметры b и α, связь между ln μ и ln s * (или w * ) линейна: ln μ= ln s * - ln a + ln η 0. Характер зависимости µ от параметра a (т.е. от скорости сдвига ν) полностью определяется зависимостью w * от a (или s * от a ). В силу связи ln μ= ln s * - ln a + ln η 0 производные ln μ и ln s * по любому из параметров b и α совпадают: μ′ / μ = s * ′ / s *. Поэтому совпадают знаки производных и интервалы монотонности величин µ и s * по b или по α.
ТЕОРЕМА 2. В предположениях теоремы 1 равновесная кажущаяся вязкость μ : =τ */ ν=η 0 s */ a выражается по формулам (13) и обладает следующими свойствами:
-
1) кажущаяся вязкость μ ( a , b , α ) монотонно убывает по параметру b , и
- μb/μ=s*b/s*=-αg(s*)w*2[1+αbw*2s*g′(s*)]-1<0,
-
2) μ ( a , b , α ) возрастает по α при любых МП и МФ, μ α/ μ= s *α / s * , т.е. μ α/ μ тоже выражается формулой (10),
и справедливы оценки 0 <μ α / μ< w * < 1, 0 <μα< w *μ = η0 w * e α w * <η0 w * e α ,
-
3) μ ( a , b , α ) убывает по a (и по η 0 , и с ростом скорости сдвига ν), ее производная по a выражается формулами μ′/μ=α w *′=-α bw * 2 g ′( s *) s *′, μ′=η0α e α w * w *′,
-
4) пределы равновесных кажущейся вязкости (13), производных напряжения и степени сшитости при a →+ 0 и a →∞ (т.е. при ν→ 0 и ν→∞ ) и начальный угол наклона s * ′ (0 + ) реологической кривой s *( a ) выражаются формулами.
μ 0 =η 0 Q , μ∞=η 0, μ 0 = Q ; s * ′ (0 + ) = Q , μ ∞
w * ′ (0 + ) s * ′ (0 + )
= - b (1 + b ) - 2 g ′ (0) ,
μ′ (0 + ) w * ′ (0 + )
=αη 0 Q ,
Q =exp(α[1+ bg (0)]-1) = e α/(1+ b ) ∈ (1, e α) (при условии
g ( +∞ ) =+∞ для пределов при a →∞ );
если g ′ (0) = 0 , то w * ′ (0) = 0 и μ′ (0) = 0 при любых МП.
Все утверждения теоремы 2 доказаны в [1]. Модель описывает возрастание реологической кривой s * ( a ), убывание кривой вязкости μ ( ν ) и существование конечных пределов вязкости при ν→ 0 и ν→∞ (максимальной и минимальной вязкостей – см. рис. 2) т.е. важнейшие качественные свойства типичных кривых вязкости, наблюдаемых для разных псевдопластических жидкостей [5–32]. Очевидно, из (14) при любых МП и любой МФ следует, что 0 <μ∞<μ 0 и μ∞> e -αμ0 , отношение μ 0 / μ∞ совпадает с начальным углом наклона s * ′ (0 + ) реологической кривой s * ( a ), зависит лишь от параметров α , b (и не зависит от МФ g ( s ), от η 0 и других МП модели (3)–(5)), причем возрастает по α и убывает по b .
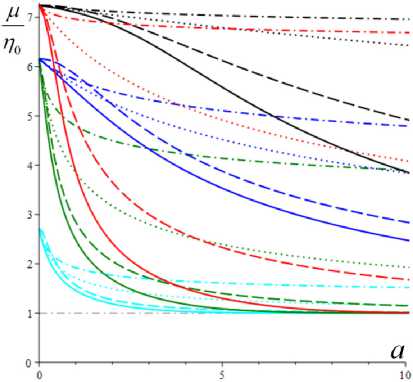
Рис. 2. Кривые (безразмерной) вязкости μ( a )/η0 , порождаемые моделями с разными МП и МФ (12)
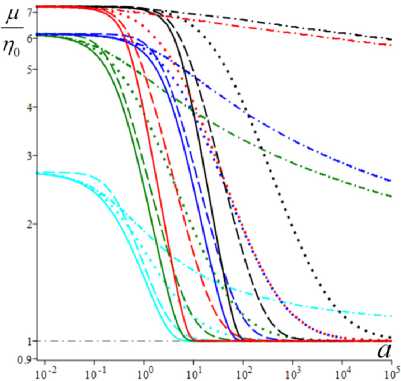
b
Fig. 2. Dimensionless viscosity curves μ( a )/η0 generated by models with different material parameters and material functions (12)
Таким образом, модель описывает общее свойство ц _ < ц 0 типичных кривых вязкости, наблюдаемых для разных псевдопластических жидкостей (часть эффекта тиксотропии).
На рис. 2, а , приведены графики зависимости от a обезразмеренной кажущейся вязкости p( a )/п0 = = T . /(vn0) = s . ( a)/a для МФ (12) (сплошные, штриховые, пунктирные и штрихпунктирные линии) и тех же пяти наборов МП с фиксированными а = 2 , в = 1 и с разными парами b и h , что и на рис. 1: b = 0,01, h = 0,1 (черным цветом), b = 0,01, h = 1 (красным), b = 0,1, h = 0,1 (синим), b = 0,1, h = 1 (зеленым) и b = 1, h = 1 (голубым). При a ^ 0 p( a )/q0 ^ Q , при a ^ ~ p( a )/n0 ^ 1; самое медленное убывание p( a ) обеспечивает логарифмическая МФ (12) (штрихпунктирные кривые). На кривых вязкости p( a ) / п0 (зависимость от скорости сдвига v получается сжатием вдоль горизонтальной оси) есть точки перегиба: выпуклость вверх сменяется выпуклостью вниз. Отношение р 0 / р _ = 7 (и, конечно, кривая вязкости такой формы) характерно, например, для расплава полиэфирэфиркетона при 400 °С. На рис. 2, b , изображены те же кривые, но в логарифмических координатах (как принято в реологии), с охватом более широкого диапазона скоростей сдвига и детализацией участка малых скоростей. На них хорошо видны горизонтальные полки - участки с максимальной и минимальной вязкостями и квазиньютоновским поведением: в диапазоне малых скоростей и больших скоростей вязкость практически постоянна: р ( a ) ~ р 0 = n 0 Q при a < a 0 и р ( a ) » р _ = п 0 при a > a _ , где a 0 = 0,1 и a _ зависят от МП и МФ модели.
В теоретическое равенство s ’ (0 + ) = р 0 / р _ входят измеряемые величины и проверка его выполнения по экспериментальным данным может служить удобным индикатором применимости модели (3)-(5) к конкретному полимеру (твердообразному материалу, раствору, расплаву, суспензии и т.п.). Равенства (14) удобны и для идентификации параметров b , а и п 0.
5. Устойчивость точки равновесия и зависимость ее типа от скорости сдвига и МП модели
Для исследования устойчивости точки равновесия и фазового портрета автономной системы (1), (2) осуществим ее линеаризацию в окрестности точки равновесия (8), (9) и найдем собственные значения линейной системы и условия, при которых они являются комплексными или действительными, простыми или кратными, исследуем знаки их действительных частей.
Линеаризация системы (1), (2) в окрестности точки равновесия (s., w.) дает линейную систему x = Ax , где x = (x1, x 2)T, x1 = s - s., x 2 = w - w., A = J( s., w.) - матрица Якоби отображения f = (f1, f, )T, задающего поле скоростей системы (1), (2) в точке (s., w.). Вычисление частных производных поля скоростей системы (1), (2) приводит к матрице an =- e(e-a)*, a12 = a aeew’, a21 = -cbw. g ‘(s.), a22 = -cw.1,
где s. = aea№, w. = F(s.) по (7). Уравнение для соб- ственных значений имеет вид
X 2 - 1 Д + 1 2 = 0, (16)
11 = a11 + a 22, 12 = det A = a11 a 22 - a^ a 21, где 11,12 - инварианты оператора A . Они и дискриминант уравнения (16) вычисляются по (15):
1 1 =- e < e-a ) w - cw - 1,
1 2 = ce (e-a) “" w - + abc a w . g '( s . ) e e “ ",
D = [e D = 112 - 412 = [cw-1 - e№]2 - 4abcaw.g'(s.)eew, (18) где cb = k2T0, abc = k2T0vn0 / Tc. Вследствие условия g'(s) > 0 и положительности s., w. и всех МП всегда выполнены неравенства I1< 0, I2> 0 и D< 112, а из w. е (0;1) и р < a следуют неравенство ee-a< e<e-a)w’ < 1 и более точные оценки: —1 — cw.< 11 < — cw.< — c , 11 < — e(e a) — c; т (в-a)w -1 . „„(в-a)w . __e-a 12 > ce w. > ce > ce , [cw—1 -1]2 - 4abcaeвw.g'(s.) < D< c2w—2 - 4abcaw.g'(s.). Поэтому все коэффициенты уравнения (16) положительны при всех значениях МП и любой МФ g(s), следовательно, у него нет положительных действительных корней и положение равновесия не может быть седлом (случай, когда у (16) есть два вещественных корня разного знака). Корни характеристического уравнения (16) вычисляются по формуле 2X = 11 ± DD = -e~(a-e)wt- cw-1± ± [(cw—1- e-(a-e)w )2- 4abcaw.g'(s.)eв”" ]1/2. ТЕОРЕМА 3 [2]. В предположениях теоремы 1 единственное положение равновесия (s., w.) (8), (9) системы нелинейных дифференциальных уравнений (1), (2) устойчиво при произвольных МП и МФ и может быть фокусом, узлом или вырожденным узлом: 1) точка равновесия - устойчивый узел, если выполнено неравенство D > 0 , т.е. [cw*1 - e<а в)w*]2 > 4abcаw*g'(s*)eew*, (20) 2) точка равновесия - устойчивый вырожденный узел, если выполнено равенство D = 0 , т.е. [cw-1 -e(а-в)w*]2 = 4abcаw*g'(s*)eew*, (21) 3) точка равновесия - устойчивый фокус, если выполнено неравенство D< 0 , т.е. [c w*1 - eЧа-Р)w* ]2< 4abcаw*g'(s*)eew* , (22) Таким образом, найдены критерии реализации каждого случая в виде неравенств (20)-(22) на МП. Седлом или центром точка равновесия быть не может: при D > 0 всегда оба корня отрицательны, ибо 11 < 0 и D < I12 (случай седла не реализуется, так как корни одного знака), а при D < 0 всегда Re X < 0 (Re X ^ 0 и центр невозможен), поскольку 2Х = I1 ± i | D |0'5 и Re X = 0.511 . Условие в виде равенства (21) не является грубым и легко нарушается из-за малейшего возмущения МП, так что фактически есть два основных случая: узел и фокус. Существование устойчивого фокуса у системы (1), (2) при ограничениях (22) на МП и скорость сдвига означает немонотонность ее решений s (t), w(t), и существование режимов деформирования с (затухающими) колебаниями напряжения и степени сшитости при выходе на стационарные значения s*, w* при t ^ ~. Отметим, что положение равновесия (8), (9) не зависит от параметров G0, в и c из (4) и (2), но тип точки равновесия (фазовый портрет системы (1), (2)) зависит от них, поскольку в и c входят в критерии (20)-(22). Поэтому управлять поведением интегральных кривых, не сдвигая положение равновесия, проще всего с помощью параметров в и c. Зависимость D(c) всегда квадратичная (ибо точка (s*, w.) не зависит от c), при c = 0 D = e-2(а-в)w* е (0;1], при достаточно больших c тоже D(c) > 0. Это означает, что при больших c положение равновесия не может быть фокусом; это верно и при достаточно малых c, если а ограничено, но если нет, то для любого c £ 0 найдется достаточно большое а(c), такое, что D(c) < 0 в (узкой) окрестности точки а(c) (правда при a ^ ~ опять D(c) > 0). Фокус следует искать в окрестности точки минимума функции D(c), т.е. точки cm = w*2[w*1 e (“ в)w* + 2abаw*g'(s,)eew*] = = w* eew [e~“w* + 2abаw*2g'(s*)] > 0. При любых МФ и МП D (cm) < 0: D(cm) = -4abаw*2e2вw*g'(s*)[abаw*2g'(s*) + e-aw* ] < 0 , т.е. всегда можно настроиться на фокус только за счет выбора МП c в окрестности значения c = cm . Зависимость D от параметра в полностью определяется зависимостью от переменной x = eew* , поскольку s* и w* не зависят от в в силу (18) D(x) = Ax2 - Bx + C, A = ew*, B = 2cw*-1e-аw* + 4abcаw* g'(s*), C = c2w*-2; xm= cw-1[1 + 2 ab а w*2g'(s*) eаw*] eаw* = = ca-s* w-1[1 + 2 b а w*2s* g‘(s*)], D(xm) = c2w-2 [1 + 2abаw*2g'(s*)eаw* ]2-- 2 c2w-2 [1 + 2 ab а w*2g'(s*) eаw* ]2+ + c2w-2= 4 bc2а s* g'(s*)[1 - b а w*2s* g'(s*)] (выкладки опущены). Таким образом, знак D(xm) = min D(в) всегда совпадает со знаком выражения 1 - bаw*2s*g'(s*), он может быть любым в зависимости от величин МП и скорости сдвига. При bаw*2s* g'(s*) < 1 D > 0 и фокуса быть не может. Зависимость D(a) сложнее. При a ^ 0 + w* ^ (1 + bГ1, s* (0+) = 0 , D ^ [c(1 + b) - e-(а-в}П1+b’ ]2 > 0, т.е. при a ^ 0 + (и фиксированных остальных МП) предел D(0+) не зависит от МФ, и положение равновесия всегда является узлом при достаточно малом а (малой скорости сдвига). А при a ^~ имеем s*(+^) = +^ , s*/a ^ 1, w* ^ 0, D ~ c2w-2 - 4abcаw* g‘(s*). Первое слагаемое стремится к +~ , а предел второго зависит от асимптотики функции f (a) = ag‘(s*)/(1+bg(s*)). Для всех моделей с МФ (12) D (+^) = +^ при любых МП. Для МФ g (s) = 1 + (hs)n, n, h > 0, f (a) = anh(hs*)n-1 / (1 + b[1 + (hs*)n ]) ^ C, C = anb-1, при a ^~ , поскольку s*(a) ~ a , и потому D (+^) = +^ . Для МФ g(s) = 1 + ln(1 + hs) имеем f (a) = ah(1 + hs*)-1 / /(1 + b[1 + ln(1 + hs*)]) ^ 0, и потому D(+^) =+^ . Для МФ g = eh f (a) = ahehs*/(1 + behs*) - ahb-1, c2w-2 = = c2 (1 + behs* )2, и потому D(+^) = +^ . Аналогично доказывается, что у всех моделей с любыми МФ (12) и любыми МП большие (меньшие по модулю) характеристические корни Х1(a) (19) стремятся при a ^ ~ к X = -1, а меньшие X2 (a) стремятся к -^ , причем X2 (a) - 11 (a) - cw*-1 = -c[1 + bg (s* (a))]. Рис. 3. Графики D(a) для четырех моделей с МФ (12) и h = 0,07 , и с МП а = 2 , в = 1, c = 0,3 (а); графики cm (a) (23) и Dm (a) для моделей с а = 2 , в = 1, b = 0,01 и МФ (12) с h = 0,07 (b) b Fig. 3. a - D(a) graph for four models with material functions (12) and h = 0.07 , and with material parameters а = 2 , в = 1, С = 0.3 ; b - cm (a) (24) and Dm (a) graph for model with а = 2 , в = 1, b = 0.01 and material functions (12) with h = 0.07 На рис. 3, а, приведены графики D(a) для четырех моделей с МФ (12) и h = 0,07, и с МП а = 2, в = 1, c = 0,3 и b = 10-12; 0,022; 0,66; 4,7 (кривые 1-4, сплошные, штриховые, пунктирные и штрихпунктирные линии для разных МФ). Балансировка моделей с разными МФ осуществлялась за счет подбора параметра b таким образом, чтобы обеспечить совпадение их положений равновесия при a = a = 400, т.е. из условия bg(s*(a)) = const. Модель с экспоненциальной МФ (12) (и b = 10-12) отличается тем, что D(a) > 0 на заметном интервале скоростей в окрестности a = 0, благодаря наличию горизонтального участка (он расширяется с уменьшением b): D(0) = 0,005, и D = 0,005 при a< 30, D = 0 при a = 37,5 (кривая 1). У моделей с квадратичной или линейной МФ (кривые 2, 3) начальный интервал с D(a) > 0 очень узок: например, для линейной МФ (кривая 3) корни уравнения D(a) = 0 равны 0,02 и 88. Кривая 5 -график D(a) для модели с той же экспоненциальной МФ, что и 1, но при c = 0,6 (с увеличенной в два раза скоростью образования сшивок k1 в (5)). Пунктирная кривая 6 - D(a) для модели с b = 0,01 и линейной МФ с h = 1. Кривая 7 - график D(a) для модели с МФ g = 1 + ln(1 + hs) с h = 1000 (и b = 1,5 по условию балансировки). Данные рис. 3 показывают, что выбор МФ g(s) может существенно влиять на поведение D(a) и тип точки равновесия (хотя предел D(0+) = [c(1 + b) - e- На рис. 3, b, приведены зависимости cm (a) (23) (черные кривые 1'-5') и Dm (a) = D(cm (a), a) (кривые 1-5) от а для тех же моделей с разными МФ, что и на рис.1: кривые 1-4 - для моделей с а = 2 , в = 1, b = 0,01 и МФ (12) с h = 0,07 , кривые 5 и 5' - для модели с такой же экспоненциальной МФ, как и кривые 1 и 1´, но с α = 0.1, β = 0. Как было доказано, D(cm) < 0 для любых МФ и МП. Для модели 1 приведены сжатые графики 0,1cm и 0, 01Dm , чтобы вписать их в область рисунка. Все функции имеют одну точку экстремума cm (a) – точку максимума, Dm (a) – точку минимума. По графикам видно, что после фиксации c = cm (a0) можно добиться уменьшения D по сравнению с D(cm ) за счет увеличения а. На рис. 4, а, приведены графики зависимости D(β) (18) для моделей с а = 2 , b = 0, 01 , c = 2 и четырьмя МФ (12) с h = 0,07 (сплошные, штриховые, пунктирные и штрих-пунктирные линии) при трех значениях a = 1;5;10 (красные, голубые, черные кривые). Для МФ g = 1 + ln(1 + hs) кривые при a = 1;5;10 сливаются. С уменьшением a интервал D(в) < 0 сужается. При a =1 все кривые (красные) для разных МФ практически совпадают. Синяя штрихпунктирная кривая - для МФ g = 1 + ln(1 + hs) с h = 1000 (кривые при a =1; 5; 10 сливаются). На рис. 4, b, приведены графики зависимости D(α) (18) для моделей с в = 1, b = 0.01, c = 2 и четырьмя МФ (12) с h = 0,07 (кривые 1-4: сплошные, штриховые, пунктирные и штрихпунктирные линии) при трех значениях a = 1;5;10 (красные, голубые, черные кривые). a b Рис. 4. Графики D (в, a) моделей с а = 2, b = 0,01, С = 2 и разными МФ (12) с h = 0,07 при a = 1;5;10 (а); графики D (a, a) моделей с в = 1, b = 0,01 , С = 2 и разными МФ (12) при a = 1;5;10 (b) Fig. 4. a - D (в, a) graph for model with a = 2, b = 0.01, С = 2 and with different material functions (12) with h = 0.07 at a = 1;5;10; b - D(a, a) graph for model with в = 1, b = 0.01, С = 2 and with different material functions (12) with h = 0.07 at a = 1;5;10 Графики для МФ g = 1 + ln(1 + hs) (штрихпунктир-ные кривые 4) сливаются друг с другом для a = 1;5;10; синяя штрихпунктирная кривая – для МФ g = 1 + ln(1 + hs) с h = 1000 при a = 10. Все кривые ныряют в область D(а) < 0 при малых а (с уменьшением в график D(а) смещается вверх, и интервал D(а) < 0 исчезает). Кривые модели с экспоненциальной МФ при a е [7;12] ныряют в нее дважды (имеют три точки экстремума); при дальнейшем росте a первый минимум исчезает (синяя кривая), область D(а) < 0 становится связной и расширяется, минимальное значение D быстро убывает, а | D‘(а) | растет. Для других МФ функция D(а) монотонно возрастает. На рис. 5–7 приведены графики функций D(α, β) , D(a, β) и D(a, c), показывающие, как изменение МП a, α, β и c приводит к отрицательности дискриминанта (18), а следовательно, к перестройке семейства интегральных кривых и появлению или исчезновению фокуса. На рис. 5, а, приведены графики D(α, β), для модели с b = 0.01, c = 3 и линейной МФ g = 1 + hs с h = 1 при a = 1 и в = 0.5i, i = 0,...,10 (кривые 0-10). При в ^ 1 (кривые 0-2) D(а) возрастает, D(а) > 0, а значение D(0, β) убывает по β. С ростом β рождается точка минимума, появляется и расширяется интервал D(а) < 0 , минимальное значение D(α) убывает, а D(0, β) быстро возрастает по β. При больших α пучок кривых постепенно стягивается в единую кривую, не зависящую от β. На рис. 5, b, приведены графики D(a, c) для модели с а = 10, в = 1, b = 0,01 и МФ g = 1 + s при c = 0,007 + 0,0005i, i = 0,...,8. Некоторые кривые D(a) пересекают ось a четыре раза (у модели – два интервала скоростей, в которых D(a) < 0 и положение равновесия - фокус). Рост параметра с вызывает смещение первой точки максимума и второй (основной) точки минимума влево и вниз и убывание максимального корня (правой границы области фокусов), при c = 0,0088 значение D(a) в первой точке максимума меняет знак на отрицательный и область D(a) < 0 становится связной (кривая 4), при c = 0,0107 первые два экстремума сливаются и исчезают (кривая 8) и у функции D(a) остается лишь один экстремум. При этом предел D(0+) = [c(1 + b) - e '" в)"'b)]2 положителен, хотя очень мал: D(0+) ~ c2. На рис. 6, а, приведены графики D(а, в) для моделей с а = 2, b = 0,01, c = 2 и МФ g = ehs, h = 0,07, при a = 1 и разных в = 0,5i, i = 0, ...,8. При в ^ 0,5 (кривые 0, 1) D(а) возрастает и D (а, в) > 0 , с ростом β рождается точка минимума, возникает и расширяется интервал D(а) < 0 , минимальное значение D(α) убывает, а D(0, β) быстро возрастает по β. При в = 1;1.5;2;2.5 (кривые 3-6) у D(а) есть два нуля, при в = 3 - четыре нуля (кривая 7), при в ^ 3.5 - два нуля. При больших α пучок кривых постепенно стягивается в одну, как и на рис. 5, а. a b Рис. 5. Графики D(а,в) модели с b = 0,01, c = 3 и МФ g = 1 + s при в = 0,5i, i = 0,...,10 (а); графики D(a,c) модели с а = 10, в = 1, b = 0,01 и g = 1+s при c = 0,007 + 0,0005i, i = 0,...,8 (b) a Рис. 6. Графики D(а,в) модели с а = 2 , b = 0,01, c = 2, МФ g = eh , h = 0,07 при a = 1 и в = 0,5i, i = 0,...,8 (а); графики D(a,в) модели с а = 2 , b = 0,01, МФ g = eh , h = 0,07 , при в = 0; 0,5;1;1,25; 1,5; 1,75; 2 и двух значениях с: c = 2 (черные) и c = 4 (голубые) (b) Fig. 5. a - D (а,в) graph for model with b = 0.01, c = 3 for linear material function g = 1 + s at в = 0.5 i, i = 0,...,10; b - D (a, c) graph for model with а = 10, в = 1, b = 0.01 and material function g = 1 + s at c = 0.007 + 0.0005i, i = 0,...,8 b Fig. 6. a - D(а,в) graph for the model with а = 2 , b = 0.01, c = 2, material function g = eh , h = 0.07 at a = 1 and в = 0.5i, i = 0,...,8; b - D (a, в) graph for the model with а = 2, b = 0.01, material function g = ehs, h = 0.07, at в = 0;0.5;1;1.25;1.5;1.75;2 and at two values of с: c = 2 (black) and c = 4 (cyan) На рис. 6, b, приведены графики D(a, β) для модели с а = 2, b = 0,01, МФ g = ehs, h = 0,07, при разных в = 0;0,5;1;1,25; 1,5; 1,75;2 и двух значениях с: c = 2 (черные) и c = 4 (голубые). С ростом в кривые прогибаются сильнее и смещаются вниз, а интервал D(a) < 0 расширяется. При малых с (c < 0.8) в окрестности точки a = 0 кривые меняются местами: по мере убывания с кривые с меньшим β двигаются вниз быстрее и оказываются ниже кривых с большим β. a b Рис. 7. Графики зависимостей D(a, c) и D(b,c) модели с а = 2, в = 1, b = 0,01, g = eh с h = 0,1 и разными значениями с Fig. 7. D(a, c) and D(b, c) graphs for the model with а = 2 , в = 1, b = 0.01, g = eh and h = 0.1 at various values of с На рис. 7 приведены графики зависимости D(a, c) и D(b,c) для МФ g = eh с h = 0,1. На рис. 7, а - графики D(a,c) для фиксированных а = 2, в = 1, b = 0,01 и разных значений c: c = 10 8 и c = 0,01; 0,1;0,5; 1; 2; 3; 3.5; 4 (кривые 0–8). Графики, пресекающие горизонтальную ось (не менее чем в двух точках, ибо D(0+) > 0 и D(м) = +м ), окрашены черным цветом, а те, что не пересекают – красным. При с → 0 (см. кривую 0) график D(a) приподнимается (по сравнению с кривой 1), при очень малых c D(a) сначала возрастает, но в окрестности некоторой точки a(c) (она сдвигается вправо с убыванием c) график резко падает вниз, пересекает ось (при а = 230 для кривой 0) и столь же быстро начинает возрастать (этот эффект связан с обращением в нуль первого слагаемого в (18) при достаточно малом c). На рис. 7, b, приведены графики D(b, c) для а = 2, в = 1, а = 1 и разных значений c: c = 0,01; 0,1;0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9 (кривые 1-10). С ростом c сначала область D(a) < 0 сначала расширяется, а затем сужается и исчезает. На рис. 8, а, приведены графики зависимостей действительной и мнимой частей корней (19) характеристического уравнения от параметра a (от скорости сдвига) для тех же четырех моделей с а = 2, в = 1, c = 0,3, b = 10-12;0,022; 0,66; 4,7 и разными МФ (12) с h = 0,07, что и на рис. 3, а, (кривые 1–4, сплошные, штриховые, пунктирные и штрихпунктирные линии). Голубые кривые 1´–3´ – три пары ветвей Im λ(a), отрывающихся от горизонтальной оси на интервале, где D(a) < 0; каждая пара образует контур, симметричный относительно оси а. Кривые 1–4 – ветви Reλ(a), абсциссы их точек ветвления - корни уравнения D = 0 , значения в этих точках вычисляются по (19): 2Х = 11 = -e(e-a)w - cw-1. Для логарифмической МФ (12) D > 0 при всех а, и корни действительны и один из них практически не зависит от а. При a ^ м у всех моделей D > 0 при большом а и ветви Reλ(a), соответствующие меньшим по модулю корням, сходятся (как доказано выше) к горизонтальной асимптоте Х = -1 (кривые 1-3 возрастают и выпуклы вверх после точки ветвления, а кривая 4 убывает и стремится к асимптоте сверху). На рис. 8, b, приведены графики зависимостей Reλ(a) и Im λ(a) характеристических корней (19) от параметра a для нескольких моделей с в = 1, b = 0,01, c = 0,005 и линейными МФ g = 1 + hs с h = 1 при разных а = 0;1; 5; 9;13,5;17; 20; 30 (кривые 0-7). Они иллюстрируют, как перестраиваются кривые с ростом α. Кривая с а = 0 (кривая 0) - для референсной модели без учета зависимости вязкости (4) от w; для нее D = [cw—1 — eew* ]2 > 0 , w* = (1 + bg(a))—1, s* = a , X1 = -eew*, X2 = -cw—1 = -c(1 + bg (a)), D = 0 при In c (1 + bg (a)) = в / (1 + bg (a)), т.е. при a »20000 . С ростом а интервал D(a) < 0 (где Im X(a) ^ 0 , а действительная часть однозначна) быстро расширяется в обе стороны, левая петля Reλ(a) постепенно стягивается к началу координат, а правая вилка удаляется от него и точки ветвления кривой 0. При а = 12 в окрестности начала координат рождается еще один интервал, в котором D< 0 (график D(a) приобретает форму кривой 3 на рис. 5, b), далее он растет вправо (кривая 4´) и соединяется с первым интервалом при а = 17 (кривая 5), а левая петля Re^(a) (где D > 0) исчезает. При дальнейшем росте α область, ограниченная ветвями кривых Im λ(a), становится выпуклой (кри- вая 7´) и распухает по вертикали. b Рис. 8. Графики зависимостей Reλ(a) и Im λ(a) характеристических корней (19) от параметра a для нескольких моделей с разными МФ вида (12) Fig. 8. Reλ(a) and Im λ(a)graphs of characteristic roots (20) for several models with various material functions (12) Дополнительно отметим, что с ростом параметра h интервал, в котором D < 0 , дрейфует влево, контур между ветвями Im λ(a) сплющивается вдоль оси а, не меняя высоты, точки ветвления Reλ(a) движутся влево строго по горизонталям, левая петля Reλ(a) сплющивается и поворачивается по часовой стрелке, а правая вилка увеличивает угол своего раствора, стремясь к прямому углу. С ростом МП с обе точки ветвления и интервал D < 0 сдвигаются влево, интервал постепенно укорачивается и исчезает при с ≈ 0,55, левая петля Reλ(a) стягивается к началу координат и исчезает (на кривой 3 рис. 8, а, область D > 0 в окрестности нуля столь мала, что не заметна). Установленные в этом разделе свойства зависимости D и λ (и типа положения равновесия) от МП и МФ модели позволяют проследить, как эволюционируют интегральные кривые и диаграммы деформирования, порождаемые моделью, выбрав наборы МП и МФ, обеспечивающие наглядное представление эволюции кривых.
6. Интегральные кривые модели и влияние на них начальных условий, МП и МФ Проиллюстрируем, как смещается точка равновесия и меняется ее тип, как перестраиваются интегральные и фазовые кривые системы уравнений (1), (2) по мере роста скорости сдвига (параметра а) на примере двух моделей с разными МФ вида (12). На рис. 9 приведены решения 5 (t) , w(t) и фазовые кривые системы уравнений (1), (2) для модели с а = 2 , в = 1, b = 10 12, c = 0,3 и МФ g = eh , h = 0,07 (в точности такой, как на рис 3, а, и 8, а, на которых кривые 1 изображают график D(a), Reλ(a) и Im λ(a)этой модели). Для этой модели корни уравнения D(a) = 0 примерно равны 37 и 415, и если а е (37; 415), то D(a) < 0 и положение равновесия (s*,w*) – фокус. Поэтому интегральные и фазовые кривые с начальными условиями 5 (0) = 0 и пятью значениями w0 = 0,02; 0,1; 0,3; 0,6; 0,9 (они маркированы цветом: голубым, черным, зеленым, синим и красным) построены при a = 10,37; 70,200,300,400;420,500 (для них D (a) = 0,005; 0,001; - 4,5; - 31; - 49; - 35,5;18,3; 245600): а, b - для a = 10 (точка равновесия (5 *, w*) = (74; 0,99999) - узел) и a = 37 (D = 0,001 ~ 0, (5*, w*) = (273; 0,9998) - вырожденный узел) графики w(t) при a = 10 и a = 37 неотличимы на взгляд, напряжения 5 (t) существенно выше при a = 37, все решения монотонно возрастают; c, d- для a = 70 ((5*, w*) = (372; 0,835) - фокус) при любом w0 напряжение превышает равновесное значение s* и возникают (затухающие) осцилляции вблизи асимптоты; e, f - для a=200 ((5*, w*) = (404;0,3 51) - фокус) вслед за начальным участком возрастания структурированности w(t) следует ее резкое падение («обрушение структуры») и постепенно затухающие колебания в окрестности асимптоты, напряжения s (t) на участке до первого максимума растут практически пропорционально времени (т.е. деформации сдвига), а затем падают и осциллируют вблизи равновесного значения (асимптоты), максимумы s (t) запаздывают по сравнению с максимумами w(t); a b Рис. 9. Решения s (t), w(t) системы уравнений (1), (2) с МФ g = eh , h = 0,07 при восьми разных значениях параметра a = 10,37; 70,200,300,400; 420,500 (с начальными условиями s(0) = 0 и w(0) = 0,02; 0,1;0,3;0,6; 0,9 ), и соответствующие фазовые кривые: а, b – для а = 10 и а = 37; c, d – для а = 70; e, f – для а = 200; g, h – для а = 300; i, j – для а = 400 и а = 420; k, l – для а = 500 d f Fig. 9. Solutions s (t), w(t) of system (1), (2) with material function g = ehs, h = 0.07 at eight various values of parameter a = 10,37; 70,200,300,400;420,500 (with initial conditions s(0) = 0 and w(0) = 0.02;0.1;0.3;0.6;0.9 ) and corresponding phase curves in vicinity of equilibrium point, showing its shift and change of its type as the shear rate increases: a, b – at а = 10 and а = 37; c, d – at а = 70; e, f – at а = 200; g, h – at а = 300; i, j – at а = 400 and а = 420; k, l – at а = 500 k h j l Рис. 9. Окончание Fig. 9. End g, h - для a = 300 ((s,,w,) = (418;0,166) - фокус) наблюдается аналогичное поведение, но равновесное значение (асимптота на рис. 9, g) напряжения выше, а структурированности - ниже, «обрушение структуры» становится еще более резким, а осцилляции w(t) и s (t) затухают немного быстрее, чем при a = 200 ; i, j - для a = 400 (D = -35,5, (s,, w,) = (438;0,046) -фокус, едва заметные осцилляции вблизи асимптоты) и a = 420 (D = 18,3, (s,, w,) = (445; 0,029) - узел) графики w(t) неотличимы визуально хотя осцилляций уже нет, напряжения s (t) при a = 420 чуть-чуть выше, формы графиков полностью идентичны, на графиках s (t) (и на диаграммах деформирования s (у)) сохранился «зуб» над асимптотой), осцилляции w(t) и s (t) затухают гораздо быстрее, чем при a = 300 ; эти графики иллюстрируют и вырожденный узел при a ~ 415,7 ; k, l - для a = 500 ((s,,w.) = (501;0,0006) - узел), «зуба» уже нет при a > 470, s (t) и s (у) монотонно возрастают и напоминают двухзвенную ломаную с «изломом» в момент резкого «обрушения структуры», соответствующего выходу фазовых кривых в зону вертикального поля скоростей; при дальнейшем увеличении а первое «звено» остается прямолинейным и его угол наклона растет, а второе звено становится все более криволинейным и выпуклым, поскольку асимптота s,(a) движется вверх (выше доказано, что s,(a)/ a ^ 1 при a ^ ^). Штриховые линии на рис. 9, b, d..., пересечение которых дает точку равновесия, - кривые (7), т.е. изоклины поля скоростей системы (1), (2), в точках которых s = 0 или w = 0 . С увеличением параметра а (с ростом скорости сдвига) равновесная степень сшитости w, (a) монотонно убывает, равновесное напряжение s,(a) возрастает (см. теорему 1), а положение равновесия (всегда устойчивое) меняет тип: узел при a < 37,5, фокус при 37,5 < a < 415,7, узел при a > 415,7. Черной штриховой линией на всех рисунках, изображающих поле скоростей и фазовые кривые системы, показана кривая (9), т.е. вторая из кривых (7), на пересечении которых лежит точка равновесия. Эта кривая не зависит от параметра а, и потому точка равновесия двигается вдоль нее (вправо) с ростом а. В точке пересечения с ней любой фазовой кривой соответствуют точкам экстремума w(t) . Влияние начальной структурированности w0 затухает все быстрее с ростом а (веер цветных кривых на рисунках все быстрее стягивается в узкую полоску, ширина которой стремится к нулю); конечно, w0 влияет на начальный угол наклона кривых s (t) и на мгновенный модуль ds/dу |у^ 0 диаграммы деформирования s(у, a). При достаточно высоких скоростях сдвига (при a > 100) для любых начальных условий наблюдается следующий «критический» сценарий (см. рис. 9, f h, j, l): сначала напряжение s (t) нарастает, структурированность w(t) сначала тоже растет или остается примерно постоянной (красная кривая), а затем w резко падает при почти постоянном напряжении (в начале этого обрушения структуры s(t) еще растет, а затем падает). Это видно и на рис. 9, e, g, i, k: участок убывания графика w(t) значительно круче предшествующего участка возрастания (кривые 1-5). Если w(0) значительно меньше равновесной величины w, , то напряжение предварительно убывает, а затем начинает нарастать вместе с w(t), пока не происходит описанное «обрушение». При последующих осцилляциях в окрестности фокуса размах отклонений и скорость изменения s (t) и w(t) уменьшаются со временем. При увеличении МП а и в размах осцилляций решений s (t) и w(t) усиливается и может превышать 50 % от установившихся значений s,, w, (если точка равновесия - фокус). При больших значениях a максимум s(t) становится невозможен ни при каком выборе w0 . На рис. 10 приведены графики решений s (t), w(t) и фазовые кривые системы (1), (2) для модели с а = 2, в = 1, b = 0,661, c = 0,3 и линейной МФ g = 1 + hs , h = 0, 07 (в точности такой, как на рис. 3, а, и 8, а, на которых кривые 3 изображают график D(a) этой модели и зависимости характеристических корней от параметра а) при w0= 0,02; 0,1; 0,3; 0,6; 0,9 . Корни уравнения D(a) = 0 равны 0,02 и 88, и потому, чтобы иллюстрировать смену типа точки равновесия и эволюцию интегральных и фазовых кривых и по мере роста скорости сдвига, они построены при a = 0,01;1;10; 50; 100;250;500 (для них 10D(a) = 0,012;-1,06;-6,01; -8,31; 3,74; 105; 470;1930): первое значение из диапазона, в котором положение равновесия - узел, последующие три - фокус, остальные - узел (см. кривые 3,3' на рис. 8, а). Уже при a = 0,01 (при очень малой скорости сдвига) появляется максимум («зуб») на графике s (t) с w0 = 0,9 , фазовая кривая огибает положение равновесия и возвращается к нему развернувшимся потоком, заметно понизив структурированность при развороте (рис. 10, d). При a = 1 едва заметный максимум зарождается и на графике s (t) с w0 = 0,6 (рис. 10, b, где совмещены кривые для a = 1 и a = 10) и растет с ростом а. При a = 1 точка равновесия уже фокус, но никаких качественных изменений кривых, кроме указанного, не заметно в выбранном масштабе рисунков: интегральные кривые s(t) при a = 1 получаются из кривых s(t) при a = 0.01 растяжением по оси s в 100 раз (осцилляции s и w очень малы и незаметны) и сжатием по времени примерно в 1,5– 2 раза (время выхода на асимптоту s (t) и w(t) немного сокращается), фазовый портрет – тоже получается растяжением рис. 10, d, по оси 5 в 100 раз, 5* = 3 (вместо 0,033), w* = 0,56 (вместо 0,60), синяя фазовая кривая загибается немного вниз, а спирали фазовых кривых в окрестности точки равновесия неразличимы. Совмещение кривых для a = 1 и а = 10 иллюстрирует как пучки кривых s (t) движутся вверх с ростом а, а пучки кривых w(t) - вниз. При а = 10 максимум зарождается и на графике 5(t) с w0 = 0,3 (зеленая кривая на рис. 10, b), при а = 100 он уже пропадает (рис. 10, g), а максимумы на кривых 5 (t) с w0 = 0,6 и w0 = 0,9 становятся менее выраженными и исчезают при а > 250, все решения 5(t) возрастают (рис. 10, h, i). Когда положение равновесия – фокус, осцилляции решений s (t) очень малы и просто незаметны. С ростом а уменьшаются отклонения кривых s (t) с разными w0 друг от друга (пучок стягивается) и функции s (t) все быстрее стремятся к горизонтальной асимптоте 5 = 5* (а), которая поднимается все выше (в силу теоремы 1 5*(а) ~ а при а ^ ~). При а = 1000 никаких качественных изменений кривых по сравнению с а = 500 (рис. 10, i, l) незаметно в выбранном масштабе рисунков: только точка равновесия сдвигается (по изоклине) до 5* = 1040 , w* уменьшается с 0,04 до 0,02, время выхода на асимптоту w(t) тоже немного сокращается. d f Рис. 10. Решения 5(t) , w(t) системы уравнений (1), (2) с а = 2 , в = 1, b = 0,66, c = 0,3 и линейной МФ g = 1 + h5 , h = 0,07, при семи значениях а = 0,01; 1;10; 50;100; 250; 500 (с начальными условиями 5(0) = 0 и пятью разными значениями w(0) = 0,02; 0,1; 0,3; 0,6; 0,9 ), и фазовые кривые: а, d - для а = 0,01; b, e - для а = 1;10; c, f - для а = 50 ; g, j - для а = 100; h, к - для а = 250 ; i, l - для а = 500 Fig. 10. Solutions 5(t) , w(t) of system (1), (2) with а = 2 , в = 1, b = 0.66 , c = 0.3 and linear material function g = 1 + h5 at seven various values of parameter а = 0.01;1;10;50;100;250;500 (with initial conditions 5(0) = 0 and five various values of w(0) = 0.02;0.1;0.3;0.6;0.9 ) and corresponding phase curves in vicinity of equilibrium point: а, d - at а = 0.01; b, e - at а = 1;10 ; c, f - at а = 50; g, j - at а = 100; h, к - at а = 250; i, l - at а = 500 g j k l Рис. 10. Окончание Fig. 10. End Структурированность w(t) немонотонна при любых а и w0 , максимумы w(t) остаются при любых а, но они все больше сдвигаются влево с ростом а, а функции w(t) все быстрее стремятся к горизонтальной асимптоте w = w* (a), которая опускается все ниже с ростом а (в силу теоремы 1 w*(a) ^ 0 при a ^^). При a > 10 видно, что w(t) с большим w0 проваливается ниже остальных (красная штриховая кривая на рис. 10, b, c, g, h). Штриховые линии на рис. 10, d, e, f…, пересечение которых определяет положение равновесия в фазовом пространстве, – кривые (7), т.е. изоклины поля скоростей системы (1), (2) в точках которых вектор скорости горизонтален или вертикален. Изоклина (9), геометрическое место точек с w(t) = 0, не зависит от а, вдоль нее двигается положение равновесия с ростом а. Пунктиром на рис. 10, j, l, приведена для сравнения изоклина (9) для модели с экспоненциальной МФ, которая была исследована на рис. 9 (сопоставление изоклин подчеркивает отличия полей скоростей для этих двух МФ и объясняет отсутствие резких обрушений и осцилляций структуры на рис. 10, в отличие от рис. 9). На сводном рис. 11, а, приведены фазовые кривые той же модели с линейной МФ, что и на рис. 10, при a = 10,50,100,250; 500 с теми же начальными условиями 5(0) = 0 и w0 = 0,02; 0,1; 0,3; 0,6; 0,9 . По мере роста параметра а (с ростом скорости сдвига) точки равновесия смещается вдоль изоклины (9) (вдоль штриховой кривой 0) и меняет тип: два фокуса, три узла. Когда точка равновесия - фокус (при a < 88), осцилляции 5 и w очень малы, спирали в окрестности точки равновесия неразличимы при таком масштабе, и фазовые кривые выглядят так же, как в узле при a = 100. Примерно при a = 200 все фазовые кривые уже приближаются к точке равновесия монотонно, слева вдоль изоклины 0 – в отличие от захода справа при a = 100 (см. красные кривые и максимумы s(t) на рис. 10, а–f). На рис. 11, b, приведены фазовые кривые модели с а = 2, в = 1, b = 10 '2' - c = 0,3 и МФ g = eh , h = 0,07 (той же модели, которая представлена на рис. 9) при a = 10, 50,100,200,420 (с начальными условиями 5(0) = 0 и w0 = 0,02; 0,1; 0,3; 0,6; 0,9 ). Они иллюстрируют влияние начальной структурированности w0 и смещение точки равновесия вдоль изоклины (9) (штриховой кривой) и смены ее типа по мере роста параметра а: узел, три фокуса, узел. a b Рис. 11. Фазовые кривые двух моделей с начальными условиями s(0) = 0 и w0 = 0,02; 0,1; 0,3; 0,6; 0,9 : а - той же модели с линейной МФ, что и на рис. 10, при a = 10,50,100,250; 500; b – той же модели с экспоненциальной МФ, что и на рис. 9, при a = 10,50,100,200,420 Fig. 11. Phase curves for two models with initial conditions s(0) = 0 and w0 = 0.02;0.1;0.3;0.6;0.9 : a - the same model with linear material function as shown in fig. 10 at a = 10,50,100,250; 500 ; b - the same model with exponential material function as shown in fig. 9 at a = 10,50,100,200,420
7. Свойства диаграмм деформирования с постоянной скоростью Безразмерные ДД с постоянной скоростью деформирования, порождаемые моделью (3), (4), (5), задаются в параметрической форме уравнениями s(t), y(t) = Yat, где t – безразмерное время (полученное делением времени на T0 ), s (t) – решение системы (1), (2) с начальным условием s (0) = 0 и произвольной начальной структурированностью w(0) = w0, w0 e [0;1], Y = T0тc /п0 = тc /G0 - безразмерный нормировочный множитель (он мог быть задан единице, если бы мы произвели обезразмеривание напряжения делением на G0 и зафиксировали тc = G0, но тогда в случае твердообразных тел рабочий диапазон безразмерных напряжений попал бы в диапазон до 0,05 и менее). Нетрудно убедиться, что производная деформации по безразмерному времени (начиная с формул (1), (2), точка обозначает производную по нему) выражается формулами Y(t) = vT0 =Ya через размерную скорость сдвига v и безразмерный параметр а. Поэтому зная решение s (t) для фиксированных а и w0 легко получить диаграмму деформирования s(γ;a,w0), или τ(γ; v, w0) (в размерном виде), исключив параметр t = у / (Ya). Все графики s(t) на рис. 9 и 10 по форме подобны диаграммам деформирования s(γ,a) с постоянной скоростью благодаря выбору нулевого начального напряжения s(0) . Семейство ДД s(γ; a, w0 ) зависит от двух параметров а и w0 , и мы исследуем характер зависимости ДД не только от деформации сдвига γ (монотонность, выпуклость, мгновенный модуль, эволюцию касательного модуля ), но и от параметров а и w0 : прежде всего, выясним, монотонно ли зависит s(γ; a, w0) от а и w0 , и как они влияют на модуль упругости (мгновенный модуль) и на асимптоту ДД s(γ;a,w0), т.е. на напряжение установившегося течения s* (см. (8)). Кроме того, исследуем, как меняется структурированность при разных МФ и МП и разных скоростях сдвига и какие необычные эффекты (непривычные свойства ДД) порождает непостоянство w по сравнению с типичными ДД структурно стабильных материалов. Доказанное ранее существование единственного положения равновесия (s*,w*) (см. (8), (9)) системы (1), (2) и его устойчивость при любых МФ и МП [1; 2] означают, что s(t) ^ s* при t ^ ^ и любая ДД обладает при у ^ ^ горизонтальной асимптотой s = s*, где напряжение установившегося течения s* = s* (a, b, а) (можно трактовать его как предел текучести) зависит от скорости сдвига по (8),(9), но не зависит от начальной структурированности материала w0 (см. рис. 9, 10). Свойства зависимости s* = s*(a, b, а) детально исследованы в [1] и перечислены в теоремах 1 и 2. В частности, с ростом параметра а (с ростом скорости сдвига) s* (a) возрастает, а w* (a) убывает, а от начальной структурированности s* (a) и w* (a) не зависят. Таким образом, модель (3)–(5) адекватно описывает ДД многих пластичных твердообразных материалов, для которых свойственны течение при постоянном напряжении и скоростная чувствительность предела текучести (а также ползучесть с постоянной скоростью и релаксация напряжений). Отметим, что все ДД, порождаемые ОС (6), тоже имеют горизонтальные асимптоты, зависящие от скорости деформирования. ПРИМЕР. Рассмотрим вырожденный случай: модель с а = 0 (тогда в = 0 в силу ограничения в 5 а), когда вязкость и модуль сдвига в (3), (4) не зависят от w*. В этом случае модель (с произвольной МФ g) распадается на классическое (линейное) уравнение Максвелла (3) и дополнительное уравнение для структурированности (5), зависящее от напряжения: s = a — у, s = a (1 — e—t) (это решение с начальным условием s(0) = 0) и w + c(1 + bg(a — ae—t)w = c - линейное уравнение первого порядка, и его общее решение выражается интегралом (квадратурой). Система (8), (9) для точки равновесия имеет аналитическое решение w* = (1 + bg(a))-1, s* = a , положение равновесия - всегда узел (не может быть фокусом): D = [cw—1 — eew ]2 = [cw—1 — 1]2 > 0, D = (c + bcg(a) — 1)2, X1 = —1, X2 = — cw* = — c(1 + bg(a)), и D = 0 тогда и только тогда, когда bg(a) = (1 — c) / c . Семейство ДД не зависит от w0 и от МФ g, имеет вид s(у;a) = a(1 — e —Y"'a)), ДД возрастают по у и a и при у ^ ~ стремятся к асимптотам s = a (эти ДД приведены для сравнения на рис. 12,13 пунктиром). Очевидно, что уменьшение а ослабляет влияние структурированности на процесс деформирования (вязкость и модуль сдвига в (3), (4) не зависят от w0) и при а ^ 0 оно постепенно отключается, и семейство ДД все меньше отличается от ДД линейной модели Максвелла. Как было установлено выше, в общем случае (при а > 0) решения s(t) системы (1), (2) могут не быть монотонными и даже могут осциллировать в окрестности прямой s = s* (когда (s*, w*) - фокус), а следовательно, и ДД s(у; a, w0) может быть немонотонной по у, иметь точки перегиба (в отличие от ДД, порождаемых линейной моделью Максвелла и общим интегральным ОС линейной вязкоупругости) и приближаться к асимптоте с любой стороны. В частности, ДД может иметь характерный вид с «зубом текучести» (см. рис. 9, 10, 12, 13). Этими особенностями ДД модели (3)-(5) отличаются от ДД, порождаемых ОС (6), которые всегда монотонно возрастают [54] (так же, как и ДД, порождаемые интегральным ОС линейной вязкоупругости изотропной среды или нелинейным ОС вязкоупругости Работнова с произвольными МФ [55]). Монотонность ДД способна обеспечить и модель (1), (2), но при определенных ограничениях на параметры (см. рис. 12, 13). Безразмерный касательный модуль ДД дs/ду = s/у = [aeew — se(в—а)w]/(Ya) в силу (1), т.е. дs / ду = Y—1eew [1 — sa—e—аw ]. Безразмерный мгновенный модуль (модуль сдвига) - предел дs / ду при у ^ 0+ , т.е. при t ^ 0+ (угол наклона касательной к ДД s (у; a, w0) в нуле): G = y—1 eew [1 — s(0)a—e"w0 ] = Y—1 eew0 = G0 т—1 eew0, а размерный - G = Gtc = G0eew0 . Таким образом, приходим к формуле (4), в которой изначально заложена зависимость модуля сдвига от структурированности. От скорости мгновенный модуль не зависит, хотя ДД (и касательный модуль при у > 0) зависят. Независимость мгновенного модуля от скорости деформирования характерна не только для модели (3)-(5), но и для линейного ОС вязкоупругости изотропной среды (с любыми функциями сдвиговой и объемной релаксации), и для нелинейного ОС вязкоупругости Работнова [55] и для нелинейного ОС вязкоупругопластичности (6) [54]. При у ^ ~, т.е. при t ^ ^ касательный модуль стремится к Y—1 eew* [1 — s*a—e—aw* ] = 0 в силу (8), (9) (т.е. длительный модуль всегда равен нулю в рамках модели (1), (2) и не зависит от скорости нагружения). Отметим, что формально это не следует из существования горизонтальной асимптоты s = s* (где s* = s*(a, b, a, w0) по (8), (9)), поскольку производная может осциллировать без затухания и не иметь предела. Итак, ДД s(у; a, w0) не обязательно монотонны и не обязательно выпуклы вверх, начальная структурированность влияет на модуль упругости (на начальный участок ДД), но не влияет на асимптоту (напряжение установившегося течения); на асимптоту влияет скорость деформирования (и выбор МП и МФ модели). Монотонности семейства ДД по w0 нет: это хорошо видно на рис. 9, c-j. Ниже будет показано, что семейство ДД s(у; a, w0) не обязано возрастать по параметру а (по скорости сдвига): a2> a1 не обязательно влечет s(у; a2, w0) > s(у; a1, w0), как у подавляющего большинства структурно стабильных материалов (они демонстрируют положительную скоростную чувствительность: чем больше скорость, тем выше лежит вся ДД) и описывающих их моделей [54; 56; 57]. На рис. 12 приведены ДД s(у; a, w0) и графики структурированности w(у; a, w0) модели с а = 2, в = 1, b = 10—12, c = 0,3 и МФ g = eh , h = 0,07 (той модели, для которой на рис. 9 и 11, b, приведены интегральные и фазовые кривые) при a = 10;37; 70,200;300,400; 500,600, и для пяти значений w0 = 0,02; 0,1; 0,3; 0,6; 0,9 (как и на рис. 9, кривые с разными w0 маркированы цветом: голубым, черным, зеленым, синим и красным). Штриховыми линиями того же цвета изображены графики w(у). На рис. 3, а, и 8, а, кривые 1 изображают график D(a) для этой модели и зависимости характеристических корней от параметра а; корни уравнения D(a) = 0 примерно равны 37 и 415, и если a е (37;415), то положение равновесия (s*, w*) - фокус; для выбранных значений а D(a) = 0,005;0,001; — 4,5; — 31; — 49; — 35,5; 18,3;245600;2-1023. -0.4 f e Рис. 12. Диаграммы деформирования s(y; a, w0) и структурированность w(y; a, w0) модели с a = 2, в = 1, b = 10 а = 600 а =500 - 12, c = 0,3 и МФ g = eh , h = 0,07 при a = 10;37; 70,200;300,400; 500,600, и для w0= 0,02; 0,1; 0,3; 0,6; 0,9 : a, b - для a = 10;37; 70; c, d - для a = 200; 300 ; e, f - для a = 400; 500; 600 Fig. 12. Stress-strain curves s(y; a, w0) and structuredness w(y; a, w0) generated by the model with a = 2, в = 1, b = 10 12, c = 0.3 and material function g = eh , h = 0.07 at a = 10;37; 70,200;300,400; 500,600 and for five values of w0 = 0.02;0.1;0.3;0.6;0.9 : a, b - at a = 10;37; 70; b, c - at a = 200;300; d, e - at a = 400;500;600 Особенности поведения кривых s(t) и w(t) этой модели подробно описаны в комментариях к рис. 9, свойства кривых s(у) и w(у) аналогичны. Отметим еще, что при a< 50 и a > 400 ДД имеют типичные очертания, свойственные экспериментальным ДД вязкоупругопластичных материалов с высокой (положительной) скоростной чувствительностью и способностью к течению при постоянном напряжении (рис. 12, а, e, f): ДД s(у) возрастают и выпуклы вверх, все ДД имеют горизонтальную асимптоту s = s,(a), напряжение течения s*(a) возрастает по параметру а (теорема 1 и рис. 1, а) и не зависит от w0, а семейство s (у; a, w0) возрастает по а и w0. Однако в диапазоне скоростей сдвига а е [70; 400], когда положение равновесия - «зрелый» фокус и очень сильно влияние колебаний структурированности, эти типичные свойства ДД утрачиваются (рис. 12, b-d): s(у) уже не монотонны и приобретают точки экстремума и перегиба, а осцилляции и переплетение кривых s(у) на рис. 12, b-e, показывают, что ДД s(у) не обязаны быть возрастающими, а семейство ДД s (у; а, w0) может не возрастать по параметру w0 . Именно на интервале а е [70; 400] (рис. 12, b-d) резко замедляется рост установившегося напряжения течения s.(а) с увеличением а (понижается скоростная чувствительность ДД). В окрестности а = 400 осцилляции s(у) становятся быстро затухающими и вырождаются в «зуб текучести» (рис. 12, e), а при дальнейшем возрастании скорости сдвига точка равновесия становится узлом, и ДД приобретает типичные очертания с хорошо выраженным прямолинейным участком при у < 2 % (рис. 12, e, f) и визуальным изломом (соответствующим обрушению структуры, описанному в комментариях к рис. 9), а напряжения течения s* (а) уже мало отличается от а (в теореме 1 доказано, что s*(а) / а ^ 1 при а ^ ^ ). Для сравнения на рис. 12 и 13 приведены (желтые пунктирные линии) ДД вырожденной модели с а = в = 0 , описанной выше, при тех же значениях а. При малых а они и их асимптоты s = а лежат значительно ниже асимптот ДД исследуемой модели (напряжения в 8-9 раз ниже на рис. 12, а), но по мере роста а асимптоты моделей сближаются и уже при а = 500 асимптоты ДД совпадают (рис. 12, f). Аналогичное развитие ситуации наблюдается и на рис. 13. Это связано с тем, что при больших скоростях сдвига структурированность быстро обнуляется и слабо влияет на вязкость: s.(а)/ а ^ 1 при а ^ ^ и ц ^ п0 при а ^ ^ и при у ^ ~. На рис. 13 приведены ДД s(у; а, w0), порождаемые моделью с а = 2 , в = 1, b = 0,66, c = 0,3 и линейной МФ g = 1 + hs , h = 0,07 (в точности той моделью, для которой на рис. 10 приведены интегральные и фазовые кривые) при разных скоростях сдвига: при а = 1;3;5;10;30;50;100 (рис. 13, а-c) и а = 100;250;500;1000 (рис. 13, e). На рис. 13, а, b, ДД при а = 1;3;5;10;50;100 (положение равновесия - фокус при а < 88 , см. кривые 3 на рис. 3, а, и 8, а) построены для пяти значений w0 = 0,02; 0,1; 0,3; 0,6; 0,9 (как и на рис. 9-12 ДД для разных w0 маркированы цветом: голубым, черным, зеленым, синим и красным). Хорошо видна зависимость мгновенного модуля от начальной структурированности и зуб текучести для густой среды (красные кривые). Уже при а = 0,01 (при очень малой скорости сдвига), когда точка равновесия - узел, появляется максимум («зуб текучести») на графике s(у) с w0 = 0,9 (рис. 10, а); при а = 1 максимум зарождается и на графике s(у) с w0 = 0.6 и растет с ростом а (синяя кривая на рис. 13, а, и рис. 10, c); при а = 10 максимум зарождается и на графике s (у) с w0 = 0,3 (зеленая кривая на рис. 13, b, и рис. 10, e), но при а = 100 он уже пропадает (рис. 13, b, и рис. 10, i), а максимумы на кривых s(у) с w0 = 0, 6 и w0 = 0, 9 становятся менее выраженными и исчезают при а > 250 (все ДД s(у) возрастают). Для модели с меньшим значением b зуб текучести становится более выраженным (более острым и высоким) и долгоживущим (рис. 14, c). Хотя для всех ДД на рис. 13, а, b, положение равновесия - фокус, осцилляции ДД s(у) очень малы и просто незаметны. На панорамных рис. 13, c, d, приведены ДД при а = 1; 10; 30; 50 и а = 100; 250;500;1000 для w0 = 0,1; 0,6; 0,9. С ростом а уменьшаются отклонения ДД s(у) с разными w0 друг от друга (пучок стягивается) и функции s(у) все быстрее стремятся к горизонтальной асимптоте s = s* (а), которая поднимается все выше (по теореме 1 s,(а) ~ а при а ^м). Поведение структурированности w(t) подробно описано и проиллюстрировано на рис. 10, поэтому подобные графики w (у) не приводятся (функции w (у) немонотонны при любых а и w0 ). На сводном рис. 14, а, приведено семейство ДД той же модели с линейной МФ, что и на рис. 10 и 13, при а = 10,50,100,250; 500,1000 (первые два значения - из диапазона, в котором положение равновесия - фокус, остальные - узел) и для двух значений w0= 0,1; 0,9 (черные и красные ДД). Как и на рис. 13, c, d, хорошо видны зависимость мгновенного модуля от начальной структурированности (при w0 = 0,9 он в 2,5 раза больше), его независимость от скорости сдвига и появление зуба текучести (кривые 1-3) для густой среды при умеренных скоростях, не разрушающих структуру слишком быстро. с Рис. 13. ДД s(у; a, w0) модели с a = 2 , в = 1, b = 0,66, c = 0,3 и линейной МФ g = 1 + hs , h = 0,07 : а, b - при a = 1;3;5 и a = 10;50;100 для w0= 0,02; 0,1;0,3;0,6;0,9 ; c - при a = 1;10;30;50 для w0= 0,1; 0,9; d - при a = 100;250;500;1000 для w0= 0,1; 0,6; 0,9 d Fig. 13. Stress-strain curves s (у; a, w0) generated by the model with a = 2, в = 1, b = 0.66, c = 0.3 and linear material function g = 1 + hs , h = 0.07: a, b - at a = 1;3;5 and a = 10;50;100 for w0 = 0.02;0.1;0.3;0.6;0.9; c - at a = 1;10;30;50 for w0 = 0.1;0.9; d- at a = 100;250;500;1000 for w0 = 0.1;0.6;0.9 На сводном рис. 14, b, приведено семейство ДД s(у; a, w0) модели с МФ g = eh , h = 0,07 (той же, что и на рис. 9 и 12) при разных скоростях сдвига, а именно при a = 10,20,3 7; 70,200,400; 500,600,700 (первые три положения равновесия – узлы, последующие три – фокусы, остальные – узлы) и для двух значений w0 = 0,02; 0,9 . В интервале скоростей a е [70;300] (ДД 4, 5 и рис. 12, c, d), когда положение равновесия «зрелый» фокус, хорошо видны осцилляции ДД; видимо, их можно трактовать и как описание моделью аналога эффекта Портевена - Ле-Шателье, а параметр w (1 — w или e—w) можно связать, в частности, с относительной плотностью подвижных дислокаций в кристалле или со средним размером зерен и с уровнем неравновесности границ зерен в поликристаллических материалах [58–65]. В окрестности a = 400 (для рассматриваемой модели) осцилляции становятся быстро затухающими и вырождаются в «зуб текучести» (ДД 6), а при дальнейшем возрастании скорости сдвига точка равновесия становится узлом, и ДД приобретает типичные очертания с хорошо выраженным прямолинейным участком при у < 2 % (красные ДД 7-9 для w0 = 0,9) или у < 6 % (голубые ДД 7-9 для w0 = 0,02) и визуальным изломом в точке у = 2, s = 475 или точке у = 6, s = 460 , соответствующей обрушению структуры, описанному в комментариях к рис. 9 (w(у) ~ 0 при у > 2 или при у > 6 - см. рис. 12, f). Существенно, что именно на интервале скоростей сдвига a е [70;400] (ДД 4-6) резко замедляется рост установившегося напряжения течения s*(a) с ростом а (понижается скоростная чувствительность ДД): s* (a) растет гораздо быстрее и при малых скоростях сдвига (кривые 1–3), и при больших (ДД 7–9), когда скорость роста s* (a) уже становится постоянной (по теореме 1 s*(a) ~ a при a ^ ^ - см. рис. 1, а). В этом интервале скоростей ДД с меньшей скоростью сдвига может на некотором интервале оказаться выше ДД с большей скоростью сдвига (см. красные кривые 4, 5 для a=70 и a=200, а также рис. 14, d), хотя для установившихся напряжений s* (a) строго соблюдается (теорема 1) возрастание по параметру а, т.е. положительная скоростная чувствительность напряжения течения. Как и на рис. 14, а, хорошо видна зависимость мгновенного модуля от начальной структурированности: при w0 = 0,9 он почти в 3 раза больше. a b c Рис. 14. Семейства ДД s(γ; a, w0 ), порожденные тремя моделями с разными МФ при разных скоростях сдвига и начальной структурированности w0: а - моделью с а = 2, в = 1, b = 0,66, c = 0,3 и МФ g = 1 + hs , h = 0,07 (как на рис. 13) при a = 10,50,100,250; 500,1000 для w0= 0.1;0.9; b - моделью с а = 2, в = 1, b = 10-12, c = 0,3 МФ g = eh , h = 0,07 (как на d рис. 12) при a = 10,20,37; 70,200,400; 500,600,700 и w0 = 0,02; 0,9; c, d - моделью с а = 5, в = 1, b = 0,01, c = 0,005, и линейной МФ g = 1 + hs , h = 1, при a = 0,1; 1; 10; 50; 100; 200 и a = 0,1; 1; 10 (крупно) для w0= 0,02; 0,1; 0,3; 0,9 Fig. 14. Families of stress-strain curves s(γ; a, w0) generated by three models with various material functions at different shear rate and initial structuredness w0: a - models with а = 2, в = 1, b = 0.66, c = 0-3 and g = 1 + hs , h = 0.07 (as in fig.13) at a = 10,50,100,250; 500,1000 for w0= 0.1;0.9; b - models with а = 2 , в = 1, b = 10 12, c = 0.3 and g = eh , h = 0.07 (as in fig.12) at a = 10,20,37; 70,200,400; 500,600,700 for w0= 0.02;0.9; c, d- models with а = 5, в = 1, b = 0.01, c = 0.005 and linear g = 1 + hs , h = 1, at a = 0.1; 1;10;50;100;200 and a = 0.1; 1;10 (close-up) for w0= 0.02;0.1;0.3 На рис. 14, c, приведены ДД модели с а = 5 , в = 1, b = 0,01, c = 0,005, и линейной МФ g = 1 + hs , h = 1, при a = 0,1; 1; 10; 50; 100; 200 (для них 104D(a) = 1,8;2;8;51; 111,234;577) и w0= 0,02; 0,1;0,3. На рис. 14, d, увеличен начальный участок ДД 1–3 для а = 0,1; 1; 10 . У этой модели положение равновесия -узел при а< 12609 и фокус при а е (12609;25365) (кривая 2 на рис. 8, b – график зависимости характеристических корней этой модели от а). Фазовый портрет и ДД этой модели в рассматриваемом диапазоне а отличаются от ДД модели с линейной МФ, рассмотренной выше на рис. 10, 11, 13, 14, а, несколькими особенностями (новыми сценариями поведения): 1) для ДД этой модели характерен выраженный и долгоживущий «зуб текучести» на кривых s(у) и s (t) для всех w0> 0,2 (см. пунктирные ДД 5, 6 для w0= 0,3 на рис. 14, c, и красные кривые для w0= 0,9), зуб растет с ростом w0; 2) наличие на ДД s(γ) с малыми w0 и невысокими скоростями сдвига (а< 50) начальных участков с выпуклостью вниз (рис. 14, d) и даже нескольких точек перегиба; 3) немонотонность семейства ДД s(γ; a, w0) по параметрам а и w0 , «переплетение» ДД с малыми w0 и невысокими скоростями сдвига (рис. 14, d). Большой рост напряжений сверх равновесного (в 2-3 раза выше s* (а) при w0= 0,9 -см. красные кривые) вызван тем, что скорость разрушения структуры растет медленно с напряжением (b = 0,01 мало), вязкость быстрее растет по w (а = 5 , увеличение α усиливает влияние структурированности на процесс деформирования), и w0 сильнее влияет на форму ДД. При определенных ограничениях на МП модель способна обеспечить и билинейную форму ДД, свойственную идеальной упругопластической модели, но со скоростной чувствительностью (рис. 15). На рис. 15, а, приведено семейство ДД s(γ; a, w0) и графики структурированности w(γ;a,w0), порожденные моделью с а = 100, в = 0, b = 0,001, c = 0,3 МФ g = ehs, h = 0,1, при а = 10n, n = —6;...;2, и а = 10; 25; 50;100;125 для начальной структурированности w0 = 0,02; 0,1; 0,3; 0,6; 0,9 . При изменении скорости сдвига (параметра а) на 8 порядков сохраняется билинейное очертание ДД, совсем не зависящие от начальной структурированности w0 : у всех ДД есть общий начальный прямолинейный участок с угловым коэффициентом G = G0eвw0 /тc = G0/тc при у < 1 %, не зависящий от скорости сдвига (стадия упругости), а с дальнейшим ростом γ все ДД резко выходят на горизонтальную асимптоту s = s*(а) (имеют «излом»). Для наглядности ДД при а = 0,001; 1; 100 выделены красным цветом. При а > 100 ДД приобретают закругленный переходный участок все большего радиуса перед выходом в режим течения при постоянном напряжении s* (a) (см. две верхние ДД при а = 100 и а = 125). Рис. 15. Семейство ДД s(γ; a, w0) и структурированность w(у; а, w0) при разных скоростях сдвига (а = 10n , n = —6;...;2) и начальной структурированности w0 для двух моделей с в = 0 , b = 0,001 , c = 0,3, МФ g = eh , h = 0,1, и а = 100 (а) или а = 50 (b) Fig. 15. Stress-strain curves family s(γ; a, w0) and structuredness w(у; а, w0) generated by the model with а = 100, в = 0, b = 0.001 , c = 0.3 , material function g = eh, h = 0.1 , at various shear rates (а = 10n , n = —6;...; 2) and initial structuredness w0 Структурированность w(γ) при этом сначала быстро растет почти до максимального значения 1 (быстро даже по времени: при всех а < 0,1 для любого w0 w(t) ~ 1 уже при t = 10), затем - после длительного периода стабильности (это дает упругий участок ДД) - падает (при а = 10 это происходит уже при t = 6 и стадия постоянства w(t) исчезает) и стабилизируется вблизи нуля (горизонтальный участок ДД). Равновесная структурированнность w» (a) убывает и w»(a) ^ 0 при а ^ ^ (на рисунке приведены графики w(y; а, w0) до а = 10). При а < 0,5 графики w(y) с разными w0 сливаются и начинают различаться только при а > 1 (см. цветные штриховые кривые при а = 10). Такое поведение ДД модели связано, прежде всего, с большим значением параметра а, которое вызывает очень быстрое возрастание вязкости р = П05*(а)/ а и равновесного напряжения »,(а) уже при очень малых скоростях сдвига (см. теоремы 1 и 2) и быстрое убывание w(y) до равновесной структурированности w»(а). На рис. 15, b, приведено семейство ДД 5(y;а, w0) и графики структурированности w(y; а, w0) модели, отличающейся только значением МП а = 50, при тех же величинах параметра а. Равновесные структурированности w» (а) в два раза выше, чем на рис. 15, а (см. теорему 1), напряжения течения 5»(а) понизились примерно на 510 % (понижение больше при малых а), ДД качественно почти не изменились, но при 10 < а < 60 появился едва заметный максимум.
8. Дальнейшие направления развития базовой модели и ее приложения Модель (3)-(5) (после аккуратной формулировки в трехмерном случае, дальнейшего исследования, детального сопоставления с данными экспериментов и необходимых модификаций и обобщения, в частности, учета влияния тепловыделения и теплообмена [28; 3436] и введения дополнительных структурных параметров и дополнительных уравнений для учета кинетики основных физико-химических процессов) будет применяться для описания испытаний битумов и их модификаций минеральными и эластомерными наполнителями, расплавов термопластов (полиэтиленов, полиамидов, по-лифениленсульфида, полиэфирэфиркетона и др.), угле-род-карбидкремниевых паст для 3П-печати и для решения краевых задач в технологиях переработки полимеров (в частности, твердофазной плунжерной экструзии, формования нитей методом экструзии расплава и вытяжки), задач ползучести с учетом накопления (и залечивания) поврежденности и кинетики химических превращений под влиянием агрессивной среды и задач моделирования сверхпластического деформирования металлов и сплавов с учетом эволюции нескольких параметров структуры (среднего размера, формы и ориентации зерен, уровня неравновесности границ зерен, плотности дисперсоидов, степени сегрегации на границах зерен легирующих элементов, облегчающих зернограничное скольжение и т.п.) [44; 58-69]. С целью расширения класса описываемых эффектов и области применимости модель (3)-(5) удобно использовать как элемент более сложных гибридных моделей в сочетании с детально исследованным ранее ОС (6) [49-55]. Заключение В статье продолжено системное аналитическое исследование свойств нелинейной структурно-реологической модели сдвигового течения тиксотропных вязкоупругопластичных сред (3)-(5), учитывающей взаимное влияние процесса деформирования и эволюции структуры (кинетики образования и разрушения межмолекулярных связей и ассоциатов макромолекул), предложенной в статьях [1; 2]. При произвольных шести материальных параметрах и (возрастающей) материальной функции, управляющих моделью, доказаны существование, единственность и устойчивость положения равновесия системы двух нелинейных дифференциальных уравнений для безразмерных напряжения и степени структурированности, к которой сведена модель, аналитически изучен ее фазовый портрет в окрестности ее положения равновесия, критерии того, что оно является узлом или фокусом, и базовые свойства кривых течения и кривых деформирования с постоянной скоростью сдвига, порождаемых моделью. Тем самым начат анализ способности модели описывать поведение как жидкообразных, так и твердообразных (густеющих, твердеющих, затвердевших) тиксотропных вязкоупругопластичных сред: эффекты скоростного и деформационного упрочнения, релаксации, ползучести, восстановления и др. Исследованы характер зависимости семейства ДД 5 > 0 от деформации сдвига у(t; 5, w0) (монотонность, выпуклость, мгновенный модуль, эволюция касательного модуля), от скорости сдвига а и начальной структурированности а = — 5 аweаw, а также от МФ и МП модели (в частности, МП, управляющих влиянием структурированности на вязкость и модуль сдвига и влиянием напряжения на скорость разрушения структуры). Доказано, что ДД могут быть как возрастающими, так и иметь участки убывания, напоминающие «зуб текучести», и затухающие осцилляции, что все ДД имеют горизонтальные асимптоты (напряжение установившегося течения), зависящие от скорости сдвига, и напряжение течения строго возрастает с ростом скорости, что их мгновенный модуль сдвига, наоборот, зависит от начальной структурированности, но не зависит от скорости. При определенных ограничениях на МП модель (3)-(5) способна обеспечить и билинейную форму ДД, свойственную идеальной упругопластичной модели, но со скоростной чувствительностью (см. рис. 15). Установлено, что семейство ДД 5 > 0 не обязано быть возрастающим ни по начальной структурированности, ни по скорости сдвига: в некотором диапазоне скоростей сдвига, в котором положение равновесия является «зрелым» фокусом и наблюдаются выраженные осцилляции кривых деформирования, возможно переплетение кривых деформирования с разными скоростями сдвига (см. рис. 14). Исследовано, как меняется структурированность в процессе деформирования в зависимости от МФ и МП, скорости сдвига и напряжения. Начальная структурированность влияет лишь на начальный участок ДД, но не влияет на их асимптоты и на установившуюся величину структурированности, которая монотонно убывает с ростом скорости сдвига. Разнообразие сценариев изменения структурированности во времени (в частности, обнаруженное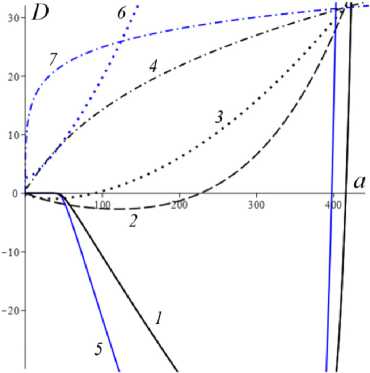
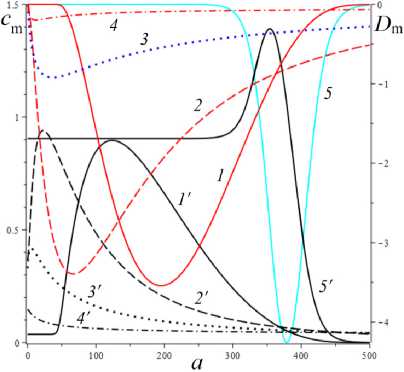
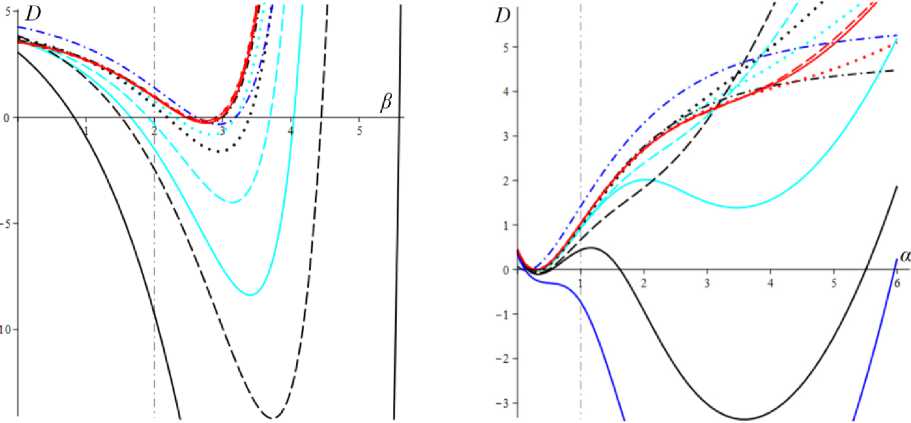
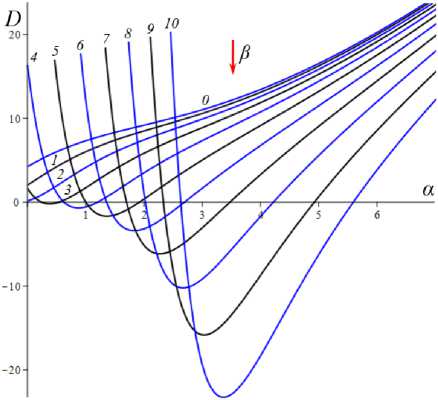
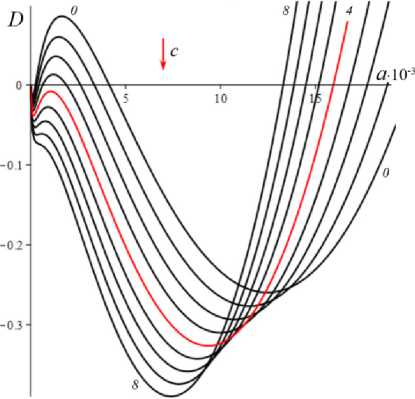
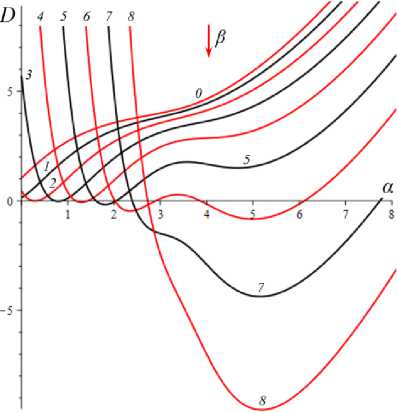
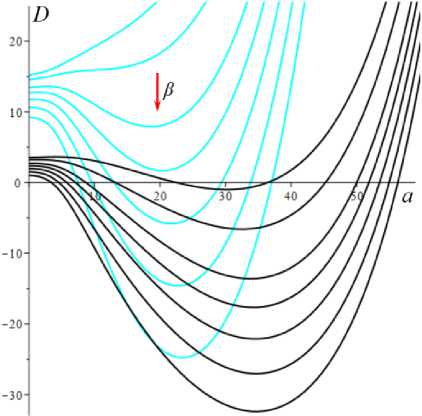
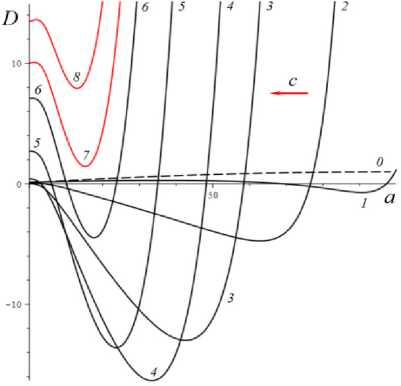
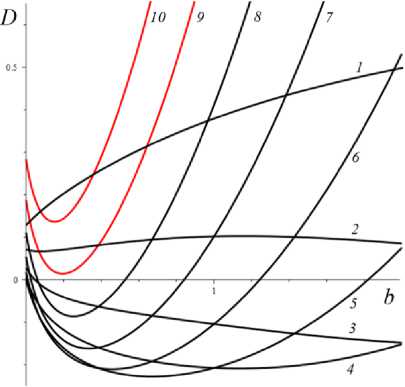
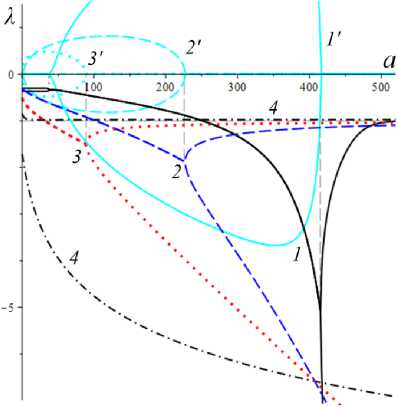
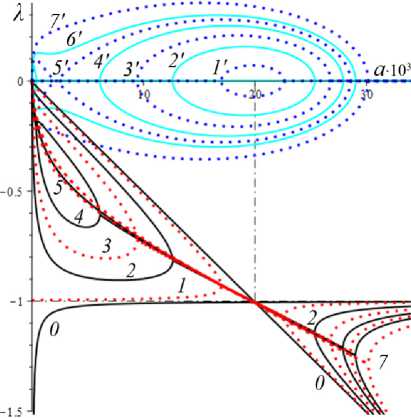
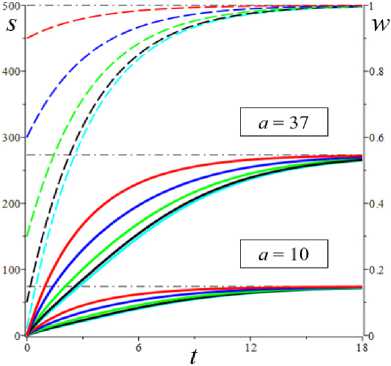
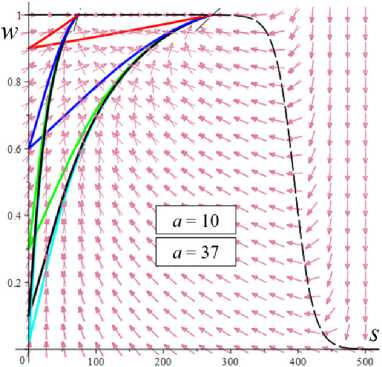
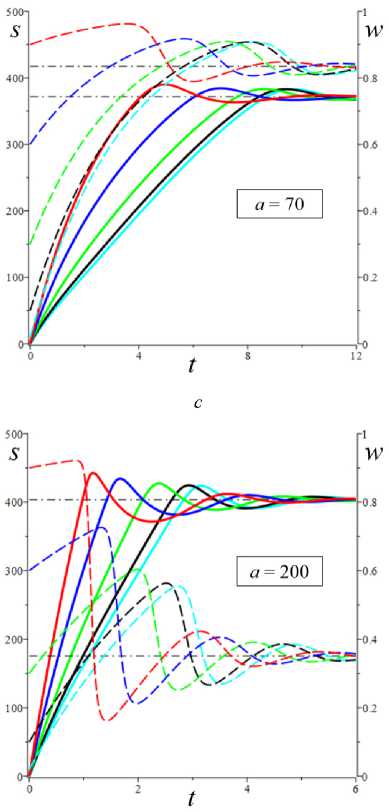
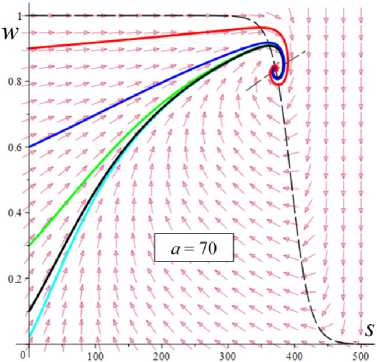
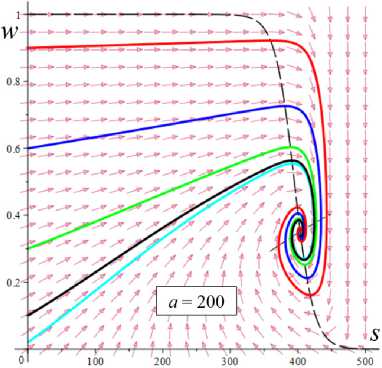
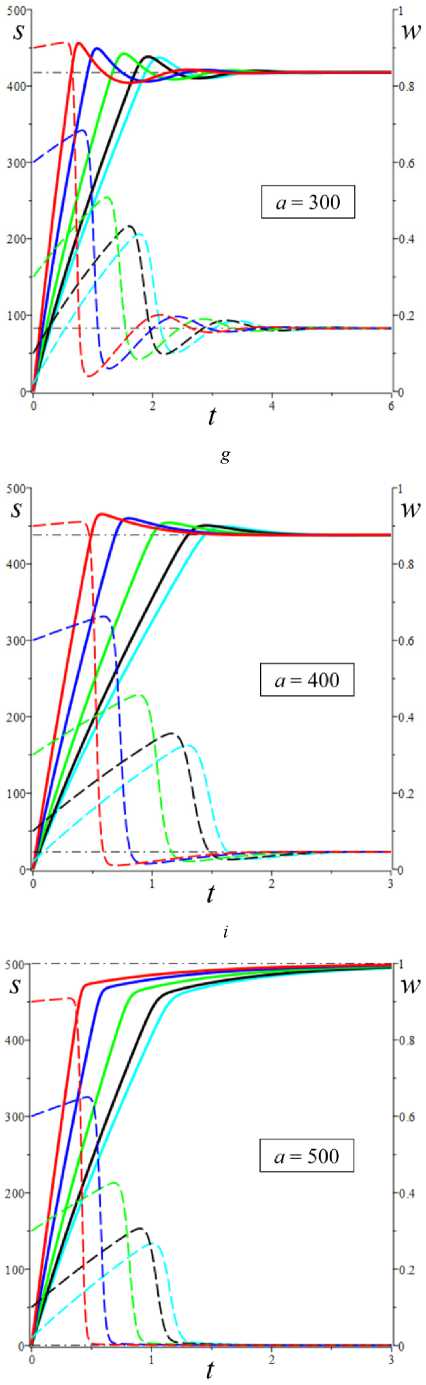
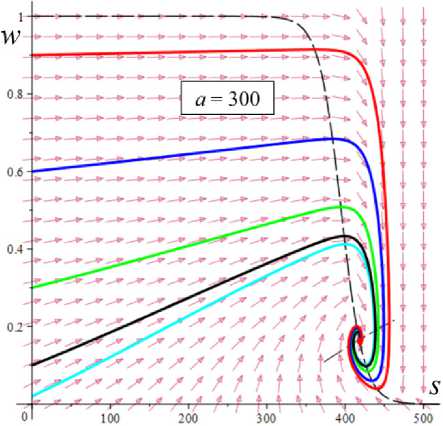
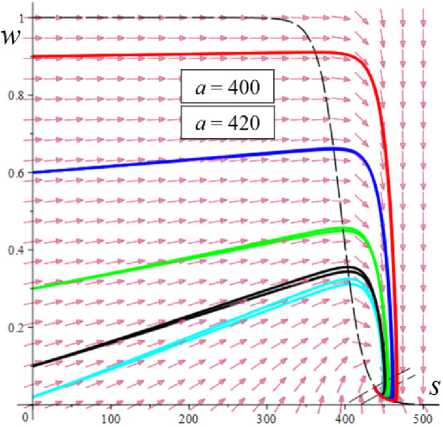
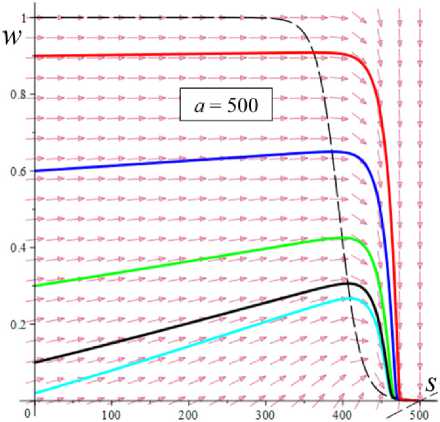
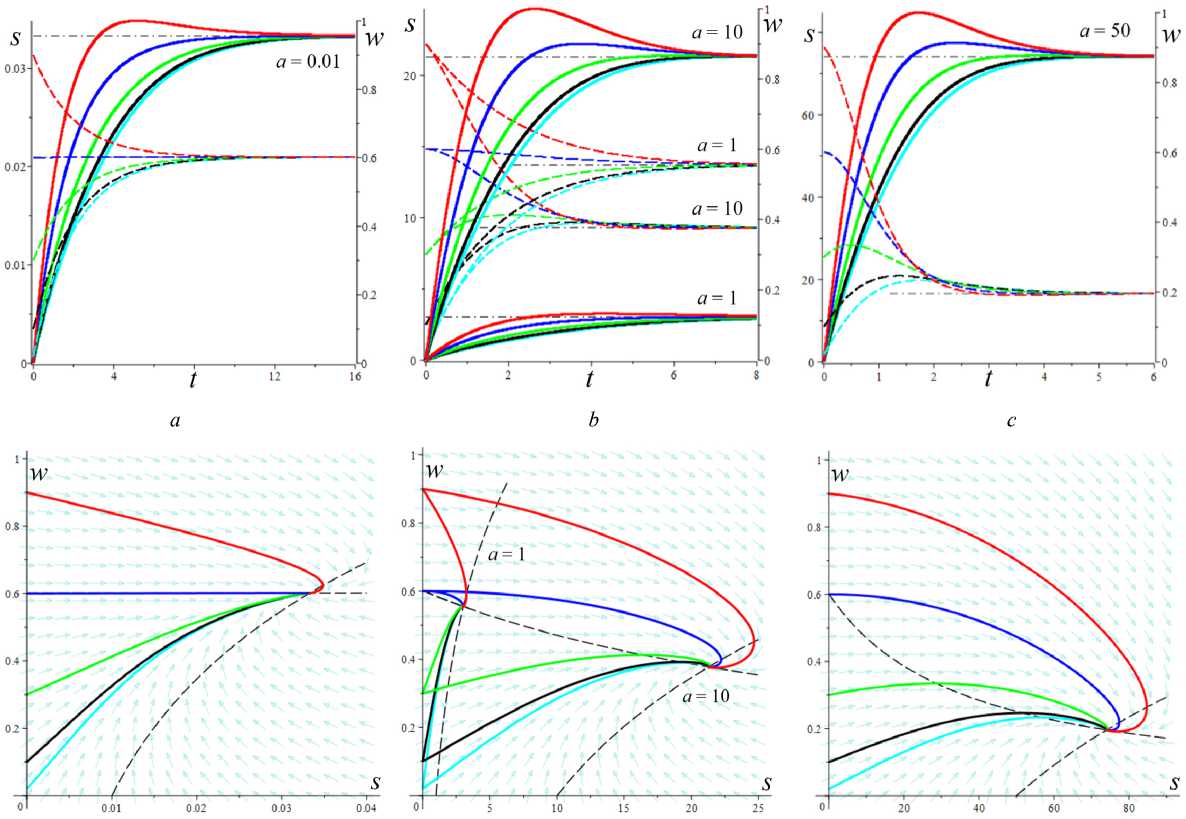
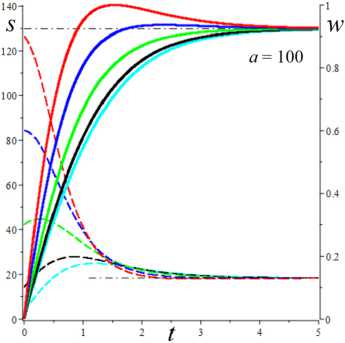
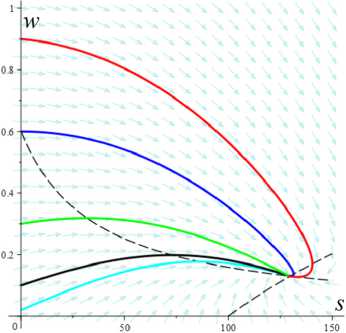
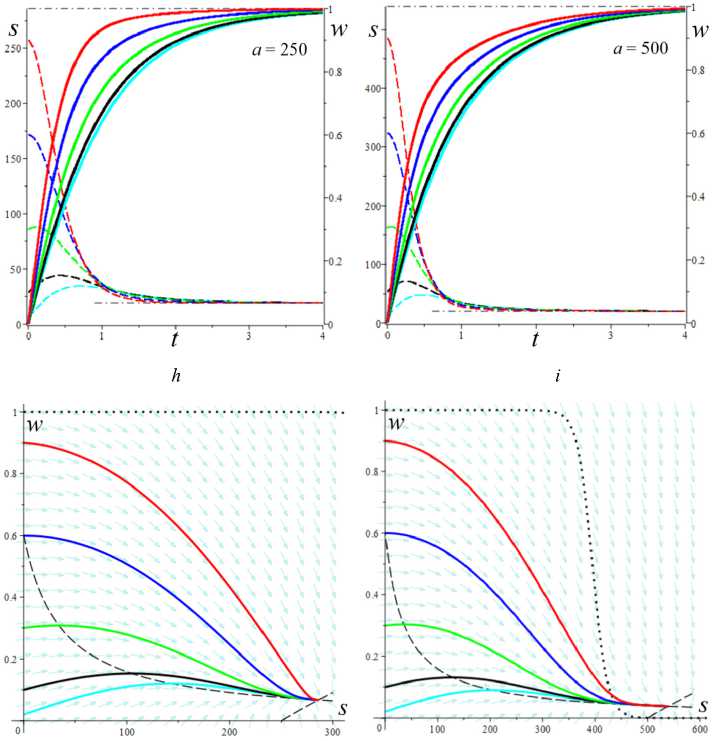
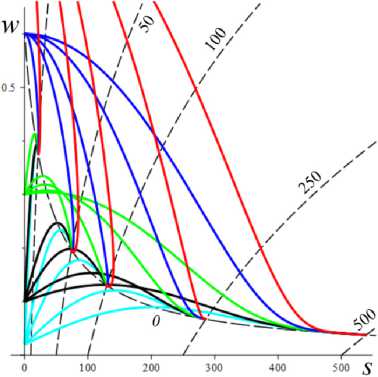
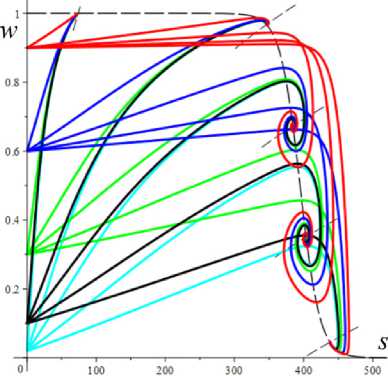
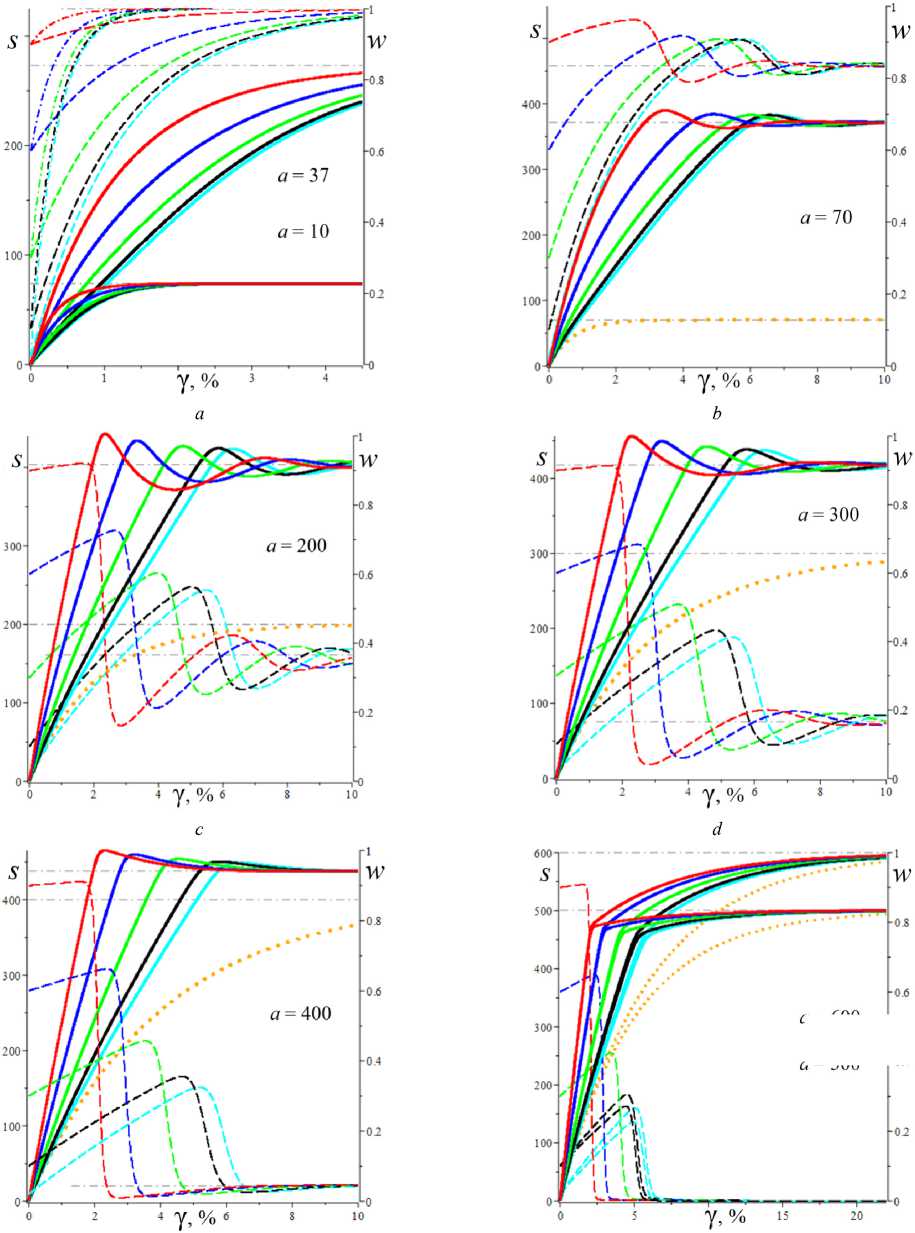
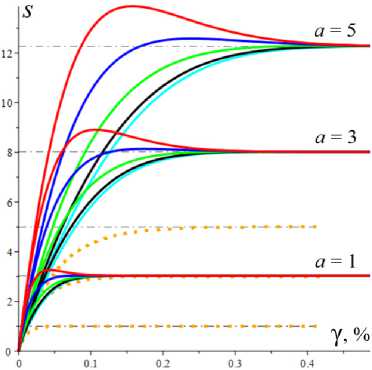
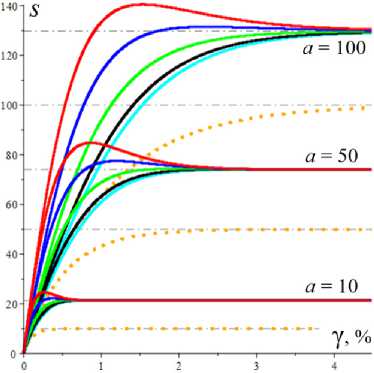
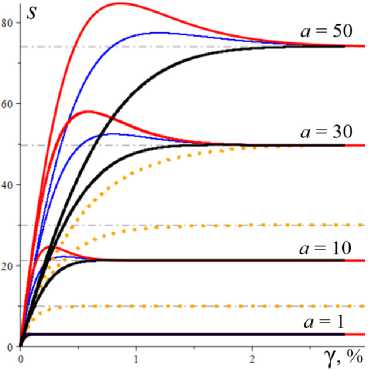
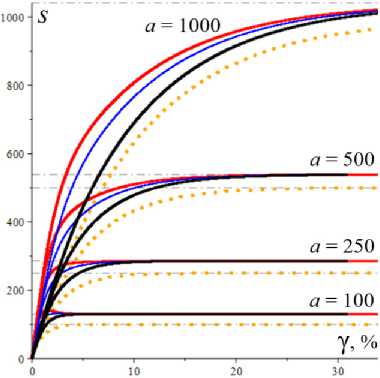
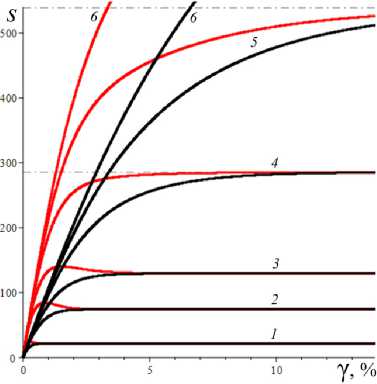
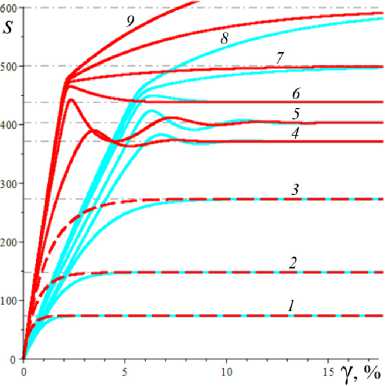
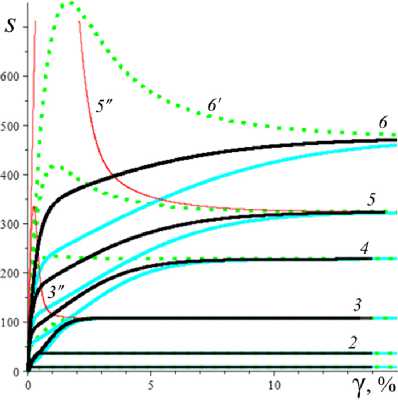
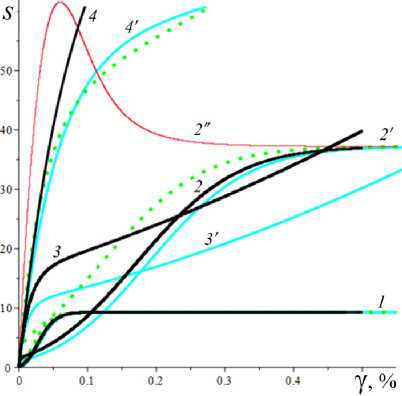
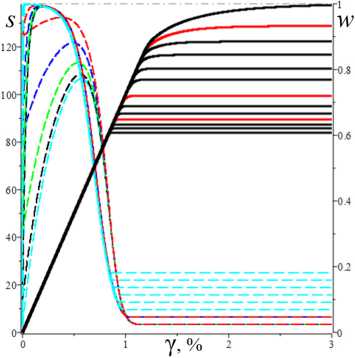
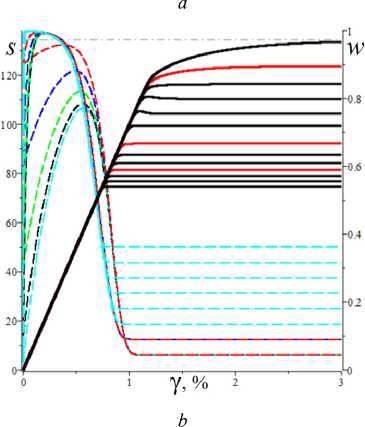
Список литературы Кривые течения и деформирования нелинейной модели сдвигового течения тиксотропных вязкоупругопластичных сред, учитывающей эволюцию структуры
- Столин, А.М. Нелинейная модель сдвигового течения тиксотропных вязкоупругопластичных сред, учитывающая эволюцию структуры, и ее анализ / А.М. Столин, А.В. Хохлов // Вестник Московского ун-та. Сер. 1: Матем. Механ. – 2022. – № 5. – С. 31–39. doi: 10.3103/S0027133022050065
- Хохлов, А.В. Точка равновесия и фазовый портрет модели течения тиксотропных сред, учитывающей эволюцию структуры / А.В. Хохлов // Вестник Московск. ун-та. Сер.1: Матем. Механ. – 2023. – № 3.
- Maxwell, J.С. On the dynamical theory of gases / J.С. Maxwell // Philos. Trans. Roy. Soc. Lond. for the year. – 1867, 1868. – Vol. CLVII. – P. 49–88.
- Bingham, E.C. Fluidity and plasticity / E.C. Bingham. – N.Y., 1922.
- Oldroyd, J.G. Non Newtonian effects in steady motion of some idealised elastico-viscous liquids / J.G. Oldroyd // Proc. Roy. Soc. London. Ser. A. – 1958. – Vol. 245. – P. 278–297.
- Reiner, M. Rheology // Encyclopedia of Physics / M. Reiner. Vol. 6. – Berlin-Heidelberg: Springer, 1958. – P. 434–550.
- Ребиндер, П.А. Поверхностные явления в дисперсных системах. Коллоидная химия. Избранные труды / П.А. Pебиндер. – М.: Наука, 1978. – 368 с.
- Coleman, B.D. Viscometric flows of non-Newtonian fluids. Theory and experiment / B.D. Coleman, A. Makrovitz, W. Noll. – Springer: Berlin – Heidelberg. – New York, 1966. – 130 р.
- Френкель, Я.И. Кинетическая теория жидкостей / Я.И. Френкель. – Л.: Наука, 1975. – 592 с
- Виноградов, Г.В. Реология полимеров / Г.В. Виноградов, А.Я. Малкин. – М.: Химия, 1977. – 440 с.
- Бибик, Е.Е. Реология дисперсных систем / Е.Е. Бибик. – Л.: Изд-во Ленингр. ун-та, 1981. – 172 с.
- Бартенев, Г.М. Физика и механика полимеров / Г.М. Бартенев, Ю.В. Зеленев. – М.: Высшая школа, 1983. – 392 с.
- Larson, R.G. Constitutive equations for polymer melts and solutions / R.G. Larson. – Butterworth: Boston, 1988. – 364 р
- Урьев, Н.Б. Физико-химические основы технологии дисперсных систем и материалов / Н.Б. Урьев. – М., 1988.
- Leonov, A.I. Non-linear phenomena in flows of viscoelastic polymer fluids / A.I. Leonov, A.N. Prokunin. – London: Chapman and Hall, 1994. – 475 p.
- Macosko, C. Rheology: Principles, Measurements and Applications / C. Macosko. – N.Y.: VCH, 1994. – 549 p.
- Schramm, G. A practical approach to rheology and rheometry / G. Schramm. – Karlsruhe: Gebrueder Haake GmbH, 1994.
- Rohn, C.L. Analytical polymer rheology / C.L. Rohn. – Munich: Hanser Publishers, 1995. – 314 р.
- Huilgol, R.R. Fluid mechanics of viscoelasticity / R.R. Huilgol, N. Phan-Thien. – Amsterdam: Elsevier, 1997. – 487 p.
- Larson, R.G. Structure and rheology of complex fluids / R.G. Larson. – New York: Oxford Press, 1999. – 387 р
- Gupta, R.K. Polymer and composite rheology / R.K. Gupta. – N.Y.: Marcel Dekker, 2000. – 390 p.
- Tanner, R.I. Engineering rheology / R.I. Tanner. – Oxford: Oxford University Press, 2000. – 451 р.
- Yamaguchi, H. Engineering fluid mechanics (fluid mechanics and its applications) / H. Yamaguchi. – Springer, 2008. – 573 p.
- Malkin, A.Y. Rheology: Conceptions, methods, applications (2-nd Ed.) / A.Y. Malkin, A.I. Isayev. – Toronto, ChemTec Publishing, 2012. – 474 р.
- Pokrovskii, V.N. The mesoscopic theory of polymer dynamics / V.N. Pokrovskii. – Springer, 2010. – 256 p.
- Гарифуллин, Ф.А. Макромолекулы и реологические уравнения. Части 1 и 2 / Ф.А. Гарифуллин. – Казань: Изд-во КГТУ. 2008. – 512 + 536 с.
- Введение в мезоскопическую теорию текучих полимерных систем / Ю.А. Алтухов, А.С. Гусев, Г.В. Пышнограй, К.Б. Кошелев. – Барнаул: АлтГПА, 2012. – 121 с.
- Столин, А.М. Неизотермические процессы и методы исследования в химии и механике полимеров / А.М. Столин, А.Я. Малкин, А.Г. Мержанов // Успехи химии. – 1979. – Т. 48, вып. 8. – C. 1492–1517.
- Прокунин, А.Н. О нелинейных определяющих соотношениях максвелловского типа для описания движения полимерных жидкостей / А.Н. Прокунин // ПММ. – 1984. – Т. 48, № 6. – C. 957–965.
- Leonov, A.I. Constitutive equations for viscoelasticliquids: Formulation, analysis and comparison with data / A.I. Leonov // Rheology Series. – 1999. – No. 8. – P. 519–575.
- Stickel, J.J. Fluid mechanics and rheology of dense suspensions / J.J. Stickel, R.L. Powell // Annual Review of Fluid Mechanics. – 2005. – Vol. 37. – P. 129–149.
- Mueller, S. The rheology of suspensions of solid particles / S. Mueller, E.W. Llewellin, H.M. Mader // Proc. R. Soc. A. – 2010. – Vol. 466, no. 2116. – P. 1201–1228.
- Malkin, A.Ya. Wall slip for complex liquids – Phenomenon and its causes / A.Ya. Malkin, S.A. Patlazhan // Advances in Colloid and Interface Science. – 2018. – Vol. 257. – P. 42–57.
- Столин, А.М. К теории сверханомалии вязкости структурированных систем / А.М. Столин, С.И. Худяев, Л.М. Бучацкий // Докл. АН СССР. – 1978. – Т. 243, № 26. – C. 430–433.
- Столин, А.М. Структурно-неоднородные режимы течения в процессе формования полимерных волокон / А.М. Столин, В.И. Иржак // Высокомолекулярные соединения, серия Б. – 1993. – T. 35, № 7. – C. 902–904.
- Беляева, Н.А. Режимы твердофазной экструзии вязкоупругих структурированных систем / Н.А. Беляева, А.М. Столин, Л.С. Стельмах // Инженерная физика. – 2009. – № 1. – C. 10–16.
- Кузнецова, Ю.Л. Влияние режимов течения на расслоение сдвигового потока жидкости c немонотонной кривой течения / Ю.Л. Кузнецова, О.И. Скульский // ПМТФ. – 2019. – Т. 60, № 1. – С. 27–36. doi: 10.15372/PMTF20190104
- Shear banding of complex fluids / T. Divoux, M.A. Fardin, S. Manneville, S. Lerouge // Annual Review of Fluid Mechanics. – 2016. – Vol. 48. – P. 81–103.
- Brady, J.F. Microstructure of strongly sheared suspensions and its impact on rheology and diffusion / J.F. Brady, J.F. Morris // J. Fluid Mech. – 1997. – Vol. 348. – P. 103–139.
- Tucker, C.L. Microstructural evolution in polymer blends / C.L. Tucker, P. Moldenaers // Annu. Rev. Fluid Mech. – 2002. – Vol. 34. – P. 177–210.
- Малкин, А.Я. Структура и реологические свойства высококонцентрированных эмульсий. Современный взгляд / А.Я. Малкин, В.Г. Куличихин // Успехи химии. – 2015. – Т. 84, № 8. – С. 803–825.
- Kulichikhin, V.G. The role of structure in polymer rheology: review / V.G. Kulichikhin, A.Y. Malkin // Polymers. – 2022. – No. 14, 1262. – P. 1–34. doi: 10.3390/polym14061262
- Perspectives on viscoelastic flow instabilities and elastic turbulence / S.S. Datta, A.M. Ardekani, P.E. Arratia [et al.] // Physical Review Fluids. – 2022. – Vol. 7, 080701. – P. 1–80. doi: 10.1103/PhysRevFluids.7.080701
- Padmanabhan, K.A. Superplastic flow: phenomenology and mechanics / K.A. Padmanabhan, R.A. Vasin, F.U. Enikeev. – Berlin, Heidelberg: Springer-Verlag, 2001. – 363+XIX p.
- Fraggedakis, D. Yielding the yield stress analysis: A thorough comparison of recently proposed elasto-visco-plastic (EVP) fluid models / D. Fraggedakis, Y. Dimakopoulos, J. Tsamopoulos // Journal of Non-Newtonian Fluid Mechanics. – 2016. – Vol. 236. – P. 104–122.
- Эглит, М.Э. Математическое моделирование склоновых потоков с учетом неньютоновских свойств движущейся среды / М.Э. Эглит, А.Е.Якубенко, Ю.С. Зайко // Труды Математического института им. В.А. Стеклова РАН. – 2018. – № 300. – С. 229–239.
- Mesoscopic single and multi-mode rheological models for polymeric melts viscometric flows description / G. Pyshnograi, D. Merzlikina, P. Filip, R. Pivokonsky // WSEAS Transactions on Heat and Mass Transfer. – 2018. – Vol. 13. – P. 49–65.
- Modeling the rheology of thixotropic elasto-visco-plastic materials / S. Varchanis, G. Makrigiorgos, P. Moschopoulos, Y. Dimakopoulos, J. Tsamopoulos // Journal of Rheology. – 2019. – Vol. 63, no. 4. – P. 609–639.
- Khokhlov, А.V. Properties of a nonlinear viscoelastoplastic model of Maxwell type with two material functions / А.V. Khokhlov // Moscow Univ. Mech. Bull. – 2016. – Vol. 71, no. 6. – P. 132–136. doi: 10.3103/S0027133016060029
- Хохлов, А.В. Кривые длительной прочности нелинейной модели вязкоупругопластичности типа Максвелла и правило суммирования повреждённости при ступенчатых нагружениях / А.В. Хохлов // Вестник Самарского гос. техн. ун-та. Сер. физ.-мат. науки. – 2016. – № 3. – С. 524–543. doi: 10.14498/vsgtu1512
- Хохлов, А.В. Нелинейная модель вязкоупругопластичности типа Максвелла: моделирование влияния температуры на кривые деформирования, релаксации и ползучести / А.В. Хохлов // Вестник Самарского гос. техн. ун-та. Сер. Физ.-мат. науки. – 2017. – T. 21, № 1. – C. 160–179. doi: 10.14498/vsgtu1524
- Khokhlov, A.V. A nonlinear Maxwell-type model for rheonomic materials: stability under symmetric cyclic loadings / A.V. Khokhlov // Moscow Univ. Mech. Bull. – 2018. – Vol. 73, no. 2. – P. 39–42. doi: 10.3103/S0027133018020036
- Хохлов, А.В. Индикаторы применимости и методики идентификации нелинейной модели типа Максвелла для реономных материалов по кривым ползучести при ступенчатых нагружениях / А.В. Хохлов // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. – 2018. – № 6. – C. 92–112. doi: 10.18698/1812-3368-2018-6-92-112
- Khokhlov, А.V. Applicability indicators and identification techniques for a nonlinear Maxwell-type elastoviscoplastic model using loading–unloading curves / A.V. Khokhlov // Mechanics of Composite Materials. – 2019. – Vol. 55, no. 2. – P. 195–210. doi: 10.1007/s11029-019-09809-w
- Khokhlov, A.V. Possibility to describe the alternating and non-monotonic time dependence of Poisson’s ratio during creep using a nonlinear Maxwell-type viscoelastoplasticity model / A.V. Khokhlov // Russian Metallurgy (Metally). – 2019. – No. 10. – P. 956–963. doi: 10.1134/S0036029519100136
- Хохлов, А.В. Двусторонние оценки для функции релаксации линейной теории наследственности через кривые релаксации при ramp-деформировании и методики её идентификации / А.В. Хохлов // Изв. РАН. МТТ. – 2018. – № 3. – С. 81– 104. doi: 10.7868/S0572329918030108
- Хохлов, А.В. Свойства семейства диаграмм деформирования, порождаемых нелинейным соотношением Ю.Н. Работнова для вязкоупругопластичных материалов / А.В. Хохлов // Изв. РАН. МТТ. – 2019. – № 2. – С. 29–47. doi: 10.1134/S0572329919020077
- Новиков, И.И. Сверхпластичность сплавов с ультрамелким зерном / И.И. Новиков, В.К. Портной. – М.: Металлургия, 1981. – 168 с.
- Nieh, T.G. Superplasticity in metals and ceramics / T.G. Nieh, J. Wadsworth, O.D. Sherby. – Cambridge: Cambridge Univ. Press, 1997. – 290 p.
- Fundamentals and engineering of severe plastic deformation / V.M. Segal, I.J. Beyerlein, C.N. Tome, V.N. Chuvil’deev, V.I. Kopylov. – New York: Nova Science Pub. Inc., 2010. – 542 p.
- Zhilayev, A.P. Superplasticity and grain boundaries in ultrafinegrained materials / A.P. Zhilayev, A.I. Pshenichnyuk. – Cambridge: Cambridge Intern. Sci. Publ., 2010. – 330 p.
- Влияние размера зерна и структурного состояния границ зерен на параметры низкотемпературной и высокоскоростной сверхпластичности нано- и микрокристаллических сплавов / В.Н. Чувильдеев, А.В. Щавлева, А.В. Нохрин [и др.] // Физика твердого тела. – 2010. – Т. 52, вып. 5. – С. 1026–1033.
- Валиев, Р.З. Объемные наноструктурные материалы: фундаментальные основы и применения / Р.З. Валиев, А.П. Жиляев, T.Дж. Лэнгдон. – M.: Эко-Вектор, 2017. – 480 с.
- Ovid'ko, I.A. Review on superior strength and enhanced ductility of metallic nanomaterials / I.A. Ovid'ko, R.Z. Valiev, Y.T. Zhu // Progress in Materials Science. – 2018. – Vol. 94. – P. 462–540.
- Шарифуллина, Э.Р. Обзор экспериментальных исследований структурной сверхпластичности: эволюция микроструктуры материалов и механизмы деформирования / Э.Р. Шарифуллина, А.И. Швейкин, П.В. Трусов // Вестник ПНИПУ. Механика. – 2018. – № 3. – С. 103–127.
- Трусов, П.В. Многоуровневая модель для описания пластического и сверхпластического деформирования поликристаллических материалов / П.В. Трусов, Э.Р. Шарифуллина, А.И. Швейкин // Физическая мезомеханика. – 2019. – Т. 22, № 2. – С. 5–23.
- Precipitation behavior and high strain rate superplasticity in a novel fine-grained aluminum based alloy / A.V. Mikhaylovskaya, A.A. Kishchik, A.D. Kotov [et al.] // Mater. Sci. Eng. A. – 2019. – Vol. 760. – P. 37–46.
- Kishchik, A.A. The microstructure and high-strain-rate superplasticity of the Al–Mg–Ni–Fe–Mn–Cr–Zr alloy / A.A. Kishchik, A.D. Kotov, A.V. Mikhaylovskaya // Phys. Met. Metallogr. – 2019. – Vol. 120. – P. 1006–1013.
- Microstructure evolution, constitutive modelling, and superplastic forming of experimental 6XXX-type alloys processed with different thermomechanical treatments / A.G. Mochugovskiy, A.O. Mosleh, A.D. Kotov, A.V. Khokhlov, L.Y. Kaplanskaya, A.V. Mikhaylovskaya // Materials. – 2023. – Vol. 16, no. 1 (Special Issue Mechanical Performance and Microstructural Characterization of Light Alloys), 445. – P. 1–18. doi: 10.3390/ma16010445


