Кручение призматических ортотропных упругопластических стержней

Введение. Законы сохранения введены в теорию дифференциальных уравнений Э. Нетер более 100 лет назад и постепенно становятся важным инструментом исследования систем дифференциальных уравнений [1–6]. Они не только позволяют качественно исследовать уравнения, но и, как показано авторами этой статьи, позволяют найти точные решение краевых задач. Для уравнений изотропной теории упругости законы сохранения впервые вычислены П. Олвером [7; 8]. Для уравнений теории пластичности в двумерном случае законы сохранения найдены одним из авторов этой статьи и использованы для решения основных краевых задач [1; 5]. Позднее оказалось, что законы сохранения можно использовать и для нахождения границ между упругими и пластическими зонами в скручиваемых стержнях, пластинах и изгибаемых балках [9–15]. В работе найдены законы сохранения для уравнений описывающих ортотропное упругопластическое состояние скручиваемого прямолинейного стержня. Предполагается, что сохраняющийся ток зависит линейно от компонент тензора напряжений. В результате найдена бесконечная серия законов сохранения, которая позволяет найти упругопластическую границу, возникающую при кручении ортотропного стержня.

Постановка задачи. Рассмотрим упругий ортотропный призматический стержень с поперечным сечением произвольной формы. Боковая поверхность свободна от напряжений, к торцам приложены силы, эквивалентны крутящему моменту М.

Пусть начало координат находится в центре тяжести торцевого сечения, а ось z параллельна образующей стержня. Граничные условия запишутся следующим образом:

Cxl + т xym = 0, т xyl + C ym = 0,                                          (1)

T xzl + T yzm = 0,

а на торцах стержня (z = 0, z = l) jj т xzdxdy = 0, JJ т yzdxdy = 0, Q          Q jj czdxdy = 0, jj xczdxdy = 0,                              (2) Q          Q jj y c zdxdy = 0. Q jj(xтyz - утxz) dxdy = M,                                     (3) Q где Q - поперечное сечение.

Как обычно в теории кручения считаем, что о x = О у = Т xy = 0.

Остальные компоненты тензора напряжений удовлетворяют уравнениям равновесия, которые запишутся так:

д = 0,    = 0, дz      дz

дт    дтУх до xz + у_ +   z_ = 0.

дx    ду    дz

Обобщенный закон Гука для ортотропной среды запишется следующим образом [16]:

д w  д и          д w  д v         д w

.

ac cTY- =     I ,  ал л Tv- = I ,  a 0^77 =

55 xz                    44 yz                    33 zz дx  дz           ду  дz           дz

Здесь a_ii упругие постоянные.

Из уравнений совместности деформаций получаем

д 2 ° z = дx 2 д 2	д 2 о z		= 5 2 ° х = 52 ? х = 0, д z 2    д x д у д         д
	д у 2 д	Л
“ n--- О 13           z д у д z	д x	V	- a 44 — T yz + a 55 — T д x        д у
д д	д	(	д         д
а7Л-----о_ 23          z дx дz	д у	V	- a 55 ^T xz + a 44 ^Т д у         д x

.

yz

' xz I ,

Из (6) и граничных условий (1) получаем, что

Из последних двух уравнений (6) следует

о z = 0 во всех поперечных сечениях.

--------1

д

' a44    T yz дX

д

⁺ a 55 ^^Т xz = const. д у

Поскольку то имеем

a 55

	a 55 T xz		9 w д и + я”, д x д z
	a 44 T ух	=	д w д v + я”, д у д z
д Д T xz д у	д - a 44 , T ух = д x	д д z	д и д v ч д у д x

-2 ^z. = -29, дz

где to _z - третья компонента вектора rot ( и , v , w ) . Поэтому 9 - есть угол закручивания на еди-

ницу длины. Он называется круткой.

Задача об упругом кручении призматического стержня свелась к интегрированию уравнений

9t z + ^TyL-о a 'Т'

⁺      = 0, “ 55^

д x    д у          д у

дт

- а44     = -29

д x

и граничному условию

т_у. / +t m = 0. xz yz

Нетрудно увидеть, что система уравнений (8) сводится к линейному уравнению второго порядка эллиптического типа.

В пластической области к уравнениям (8) следует добавить условие пластичности, которое имеет вид

^{2 а} 13 ^т xz + ^{2 а} 23 ^Т yz = 1.

Здесь а ₁₃, а ₂₃ - постоянные, характеризующие текущее состояние пластической анизотропии.

В результате получаем следующую задачу: найти для уравнений (8) законы сохранения, которые позволяют решить задачу (9). С помощью этих законов будет найдена граница между упругой и пластической областями.

Законы сохранения для уравнений ортотропной упругости . В этой части будут приведены законы сохранения для уравнений (8), для того чтобы их использовать далее для решения упругопластических задач.

Для простоты дальнейших выкладок запишем систему (8) в виде

F 1 = u x + v y ^- f ¹ = 0,

F, = аUy-вVy - f2 = 0, где u = тxz, v = тyz, а = a55, в = a44, индекс внизу обозначает производную по соответствующей переменной.

Назовем вектор ( A, B ) сохраняющимся током для уравнений (10), если

A x + B y =П 1 ( F ) + П 2 ( F 2 ) = 0,                             (11)

выполнено на всех гладких решениях системы (11). Здесь П i - некоторые не тождественно равные нулю линейные дифференциальные операторы.

В этом случае (11) является законом сохранения для системы (10).

Поставим задачу найти законы сохранения для (10), если сохраняющийся ток зависит только от x , y , u , v .

Замечание. Ничто не мешает нам найти законы сохранения и с сохраняющимся током зависящим от любого числа производных, но мы ограничимся только указанными, поскольку иные законы сохранения еще не нашли своего применения для решения краевых задач.

Пусть

A = а ¹ u + в ¹ v + Y ¹, B = а ² и + в 2 v + Y ², где а i , в i , Y i функции только от x , y .

Из (11) имеем

аru + а ux + вvV + в Vy + Yr + аvu + а ux + вVv + в Vv + Yv = xxxxxyyyyy

= 81 (ux + vy - f 1 ) + 82 (аuy - вVx - f 2).

Из (13) получаем

аX + аy = 0, вX + вУ = 0, а1 =в2 = 81, в1 = -82в, а2 =82а, yx +Y 2 =—81 f1 -82 f 2?1в = -а2/а.

Окончательно имеем

a1 + a2 — 0,—ay xy   x

a

-

i л i            ы aay = 0, Yx + у y —-af--f а

.

Для простоты считаем, что у ² — 0 . Тогда получаем:

п 1 - R2o1_ Р „2 1 _ a — р , р —--a , у —

а

-

-

а

,

а коэффициенты a ¹ и a ² связаны уравнениями:

a ¹ + a ² — 0, Ba ² - aa ¹ — 0.

xy  xy

Найдем два особых решения этой системы.

Они имеют следующий вид.

Первое решение:

al — —

x

x

в/ ГУ

, a ^y

x

y

Р/ у ²

/ Cf ^

.

Второе решение:

ai — —

x

—, a ² y ²

x

x

■

ГУ

.

Для простоты дальнейших вычислений положим

= q .

^{7 a} / a 55

Далее заметим, что уравнение (16) допускают симметрии вида: x' — x + x0, у‘ — у + у 0 , где x0, y0 – произвольные постоянные.

Поэтому полученные решения можно записать в виде:

i           x - x₀             2           y - У о

ai — 7------------ai— 7------2------^,

(x - x 0) + q (у - у 0)         (x - x0) + q (у - у 0)

• a , — q ( ^y - ^y 0 )----- , a ₂ —-------- '-------_

( ^x - ^x 0 ) + q ( y ^- y 0 )        ( ^{x - x} 0 ) + q ( y ^- y 0 )

Нами получено два сохраняющихся тока.

A — a’u - qa2v + у,1, Bi — a2u + a^v, следовательно, получено два закона сохранения

• dr A +d, B, — 0.

xiyi

Из (19) получаем:

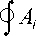
dy - B i dx — 0,

Г

где Г₁ - контур, не охватывающий точку ( x ₀, у ₀ ) .

Пусть теперь точка ( x ₀, у ₀ ) лежит внутри области D , границей которой является контур Г . В этом случае формула (20) непосредственно применена быть не может, потому что внутри контура есть особая точка. Следовательно, используем стандартный прием: описываем вокруг точки ( x ₀, у ₀ ) эллипс следующего вида: ( x - x ₀ ) ² + q ( у - у ₀ ) ² —е ² (рис. 1).

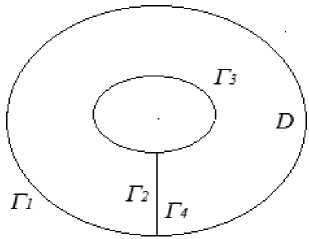
Рис. 1. Вычисление контурного интеграла вокруг особой точки

Fig. 1. Calculation of the contour integral around a singular point

Обозначим этот эллипс Г1 . Тогда без труда получаем

С A i dy - B i dx = -< С ( A i dy - B i dx ) ,

Г

Г

Вычисляем интеграл, стоящий в правой части формулы (21) для i = 1,2 .

Пусть i = 1 . Имеем

Г 1

( x - x0 )

Г, ((x - xо )2 + q ( у - у о )2 (У - У о)

и -      q(У - У о)

( ^{x - x} о ) ² + q ( У ^- У о ) ²

(x - x о)

v + y 1 dy

-

( x ^- x о ) ² + q ( y ^- у о ) ²     ( x ^- x о ) ² + q ( y ^- у о ) ²

v dx =

.

(x - xо)    q (y - у о)

----------- и--;-----------

е ²

е ²

v + y 1 dy

-

( у - у о L . (x - x о) и +

I е2

е ²

^

v dx .

У

Введем обозначения x - x0 = е cos 9, y - y0 = е sin 9 .

Имеем sin 29

v

2 п

+ y1 I d9 = q J и (xо +е cos 9, уо +е sin 9)d9.У         о

В полученном выражении устремляем е к нулю и, используя теорему о среднем, получаем

(^ = ^{2 п} qu ( x о , У о ) .

Г 1

Теперь из формулы (21) имеем

Рассмотрим случай

2 п qu ( x _о, y _о ) = - | A 1 dy - B 1 dx .

Г i = 2. Аналогично получаем:

- q (У - У о)

Г ГU x - xо ) + q (y - y о) (x - x о)

^^^^^^B

2 u ^-

( x - x о ) ² + q ( y - у о ) ²

и +

q (x - x о)       .

( x ^- x о ) 2 + q ( у ^- у о ) 2

q ( у - у о)

( ^{x - x} о ) ² + q ( У ^- У о ) ²

v + y 2 dy

v dx =

^^^^^^e

.

q ( у - у о)    q (x - x о)

---------и--

е ²

е ²

v + Y 2 dy

^^^^^^^

^( x - x о) u - q (у - у о) v'

\

е ²

dx

У

Введем координаты x - x 0 = s cos 9 , y - y 0 = s sin 9 .

Имеем

Г 1

x Г (—q +1) sin29Cp --------------u - qv

Г 1 L        ²

d 9 =

2 n

= - q j v ( x ₀ + e cos 9 , y ₀ + e sin 9 ) d 9 = - 2 n v ( x 0 , y ₀ ) q .

Теперь конкретизируем эти законы сохранения для кручения призматического стержня. Имеем

^{2 n} q ^T xz ( x 0 , y 0 ) = ^ ( ^а 1 ^т xz ^- q ^a 2 ^T yz ^{+ 2 9} J ^а 1 dx ) dx ^- ( ^a 2 ^T xz ^{+ а} 1 ^т yz ) dy , Г

2n q т yz (x 0, y 0 ) = cf(a2 т xz - q «2 т yz + 29ja2 dx) dx-(а2т xz +а2т yz) dy Г

Упругопластическая граница в скручиваемом прямолинейном ортотропном стержне. Рассмотрим упругопластическое кручение ортотропного прямого стержня, поперечное сечение которого ограниченно выпуклым контуром Г.

При достаточно большом значении крутящего момента в стержне образуется упругая зона F и пластическая зона P (рис. 2).

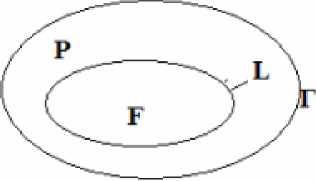
Рис. 2. Поперечное сечение скручиваемого стержня

Fig. 2. Cross-section of the twisted rod

Известно, что пластическая зона, начинает образовываться на внешнем контуре Г . Предположим, что пластическая зона полностью охватывает внешний контур. Пусть L – граница раздела упругой и пластической зон.

Цель этого параграфа – с помощью законов сохранения построенных в предыдущих параграфах, в явном виде построить границу L .

Постановка задачи. В упругой зоне компоненты тензора напряжений удовлетворяют уравнениям (8)

dl xz . ₊^dT y L-o _a ⁵ T x^ +      = 0 , a 55

dx   dy          dy

^^^^^^e

dTvz a 44 -xF" = -29, dx

а на внешнем контуре Г граничному условию

и условию пластичности

т xz1 + т yz m = 0                                            (26) 2 а 13 т 2 z + 2 а 23 т 2 z = 1.                                          (27)

Из соотношений (27)-(28) можно определить компоненты тензора т _xz , т y_z на контуре Г.

Имеем

т I = тxz |г

^т yz 1г

m

+ 2 а 23 1

l

^ 2 а ₁₃ m ² + 2 а ₂₃ 1²

Здесь знаки выбраны в соответствии с крутящим моментом (3).

В (24) нами получены следующие законы сохранения:

^{2 п} q ^т xz ( ^x о , у о ) = -I" A i dy ^- B i dx

Г

и

^{2 n} q ^T yz ( ^x о , У 0 ) = ^-( ^ A 2 dy ^- B 2 dx .

Г

Для вычисления т _xz ( x 0 , y 0 ) и т _yz ( x ₀, y ₀ ) воспользуемся формулами (29)-(30). Из этих формул получаем т _xz и т yz во всех точках внутри стержня. Теперь проверим условие (27). Те точки, в которых выражение в первой части (27) меньше единицы, попадут в упругую зону, а остальные точки в пластическую.

Заключение. Эти вычисления позволяют с любой точностью восстановить искомую границу L. Для изотропного случая эта задача решена впервые в [12; 14]. Примеры построения упруго-пластических границ для различного вида прокатных профилей рассмотрены в [10].