Круговая поляризация до и после острого фокуса для света с линейной поляризацией
Автор: Стафеев Сергей Сергеевич, Зайцев Владислав Дмитриевич, Котляр Виктор Викторович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 3 т.46, 2022 года.
Бесплатный доступ
Рассмотрена острая фокусировка света с линейной поляризацией. С помощью формализма Ричардса-Вольфа показано, что до и после плоскости фокуса имеются области, в которых поляризация круговая (эллиптическая). При переходе через плоскость фокуса направление вращения вектора поляризации в этих областях меняется на противоположное. Если до фокуса в некоторой области была левая круговая поляризация, то в самом фокусе в этой области будет линейная поляризация, а после фокуса в аналогичной области будет правая круговая поляризация. Этот эффект позволяет использовать линейно поляризованный свет для вращения вокруг своего центра масс диэлектрических микрочастиц с небольшим поглощением.
Линейная и круговая поляризации, острая фокусировка, формулы ричардса-вольфа, вектор стокса, спиновой угловой момент
Короткий адрес: https://sciup.org/140294990
IDR: 140294990 | DOI: 10.18287/2412-6179-CO-1070
Текст научной статьи Круговая поляризация до и после острого фокуса для света с линейной поляризацией
Под острой фокусировкой лазерного излучения понимают фокусировку света линзами с высокой числовой апертурой, такую, при которой нельзя уже пренебречь векторной природой световой волны. В данном случае для расчета светового поля в фокусе необходимо принимать во внимание все компоненты напряженности электрического (или магнитного) поля световой волны. Классические формулы для расчета светового поля в остром фокусе были получены Ричардсом и Вольфом в работе [1].
В настоящее время известно большое количество работ, посвященных острой фокусировке света. Однако большая часть работ посвящена изучению поведения интенсивности в фокусе, например, получению фокусных пятен различной формы [2–7]. Значительно меньше представлено работ по изучению других характеристик светового поля, таких как поток энергии (вектора Пойнтинга) [8–10], спинывой или орбитальный угловой момент [11–14]. Отметим также, что в основном внимание исследователей сосредоточено на изучении поведения света непосредственно в фокусе, поведению света на некотором отдалении от плоскости острого фокуса уделяется уже меньше внимания.
В данной работе рассмотрена острая фокусировка света линейной поляризации. Было показано, что при отдалении от плоскости фокуса возникают области, в которых поляризация перестает быть линейной. При этом при переходе через плоскость фокуса направление поляризации в этих областях ме- няется на противоположное – в областях с правой круговой поляризацией направление меняется на левую круговую и наоборот.
Теоретическое основание
В [1] получены выражения для проекций вектора напряженности электрического поля в фокусе апла-натической системы. Вектор Джонса для начального поля с линейной поляризацией, направленной вдоль оси y , имеет вид:
E ип = A (9)
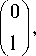
а проекции вектора напряженности электрического и магнитного полей вблизи фокуса для начального поля (1) имеют вид:
E x = - iI 2,2 sin2ф,
E y =— i ( 1 0,0 — 1 2,2 cos2ф ) ,
Ez = -21у sin ф,
Hx = i (10,0 +12,2 cos2ф),
Hy = iI2,2 sin2ф,
Hz = 21у cos ф, где
I У , Ц
= 1 f- I [sinv+1(9)cos3-v(9)X
( X JJ 0 2 2
X cos1/2 (9) A (9) ek cos9 J, (x) d 9, где λ – длина волны света, f – фокусное расстояние апланатической системы, x = krsinθ, Jμ (x) – функция Бесселя первого рода и NA = sinθ0 – числовая апертура. Начальная функция амплитуды A(θ) (предположим, что это действительная функция) может быть константой (плоская волна) или в виде Гауссова пучка. Из (2) можно получить распределения интенсивности каждой компоненты электрического вектора в фокусе
Ix = 122 sin2(2ф),
Iy = 102,o +122 cos2 (2ф) - 210,012,2 cos(2ф), (4)
Iz = 41у sin2(ф).
Из (4) видно, что распределение интенсивности I x горизонтальной проекции электрического вектора в плоскости фокуса будет иметь вид четырех локальных максимумов (световых пятен), центры которых расположены на окружности с центром на оптической оси и которые лежат на лучах, исходящих из центра под углами φ = π /4, 3π /4, 5π /4, 7π /4. Распределение интенсивности I y будет иметь вид почти круглого пятна с максимумом на оптической оси I y = 1 0 2 ,0 . Отличие от круглой формы пятна возникает из-за того, что по вертикальной оси распределение интенсивности I y будет больше ( I y = ( I 0,0 + I 2,2 ) 2), чем по горизонтальной оси ( I y =( I 0,0 – I 2,2 ) 2). Распределение интенсивности (4) в фокусе продольной компоненты электрического вектора I z будет иметь вид двух световых пятен, центры которых лежат на вертикальной оси. Такой вид распределения интенсивности отдельных компоненты электрического вектора приводит к тому, что распределение полной интенсивности в фокусе имеет вид эллипса, вытянутого вдоль вертикальной оси:
I = Ix + Iy + Iz = I02,0 + I 2,2 + 2 11,1 --2 (12 + 10,012,2 )cos(2ф).
Найдем далее продольную компоненту вектора спинового углового момента (СУМ) вблизи фокуса поля (1), воспользовавшись формулой:
S = Im (E *xE), (6)
где Im - мнимая часть числа, x - знак векторного умножения, * – знак комплексного сопряжения. Подставляя из (2) в (6), будем считать, что интегралы (3) комплексные, так как z отлично от нуля. Получим:
Sz = 2Im (Ex* Ey) = 2 sin(2ф) x
x Im (12,2 (10,0 - cos(2ф) 12,2)).
Выделим реальные и мнимые части у интегралов, входящих в (7) I 0,0 = R 0 + iI 0 , I 2,2 = R 2 + iI 2 . Тогда вместо (7) запишем:
Sz = 2sin(2ф) (10R2 -12R0). (8)
В интегралы R 0 , R 2 в (8) входит сомножитель cos ( kz cos θ) ≈ 1 при kz << 1, а в интегралы I 0 , I 2 входит сомножитель sin ( kz cos θ) ≈ kz cos θ при kz << 1. С учетом этого, вместо (8), запишем:
Sz « 2kz sin(2ф) (10R2 -12R0). (9)
В (9) использованы обозначения:
R 0 = I 0,0 ( z = 0) , R 2 = I 2,2 ( z = 0) ,
I 0 = I 0,0( z = 0) , I 2 = I 2,2 ( z = 0) ,
1 v , H
9 9 9
J sinv+1(-)cos3-v (-) x 022
x cos3/2(9) A (9) eikz cos 6 Jц (x) d 9.
Пусть на окружности некоторого радиуса выраже н ие в круглых скобках в (9) больше нуля 1 0 R 2 - 1 2 R 0 > 0 , и так как синус двойного угла в (9) положителен в 1-м и 3-м квадрантах и отрицателен во 2-м и 4-м, то до фокуса ( z <0) продольная компонента СУМ S z в (9) будет положительна во 2-м и 4-м квадрантах и отрицательна в 1-м и 3-м. И так как знак всего выражения после фокуса ( z >0) поменяется на противоположенный, то продольная компонента СУМ S z в (9) будет положительна в 1-м и 3-м квадрантах и отрицательна во 2-м и 4-м. Это означает, что до фокуса во 2-м и 4-м квадрантах вектор поляризации будет вращаться против часовой стрелки (правая круговая или эллиптическая поляризация), а после фокуса в этих квадрантах вектор поляризации будет вращаться по часовой стрелке (левая круговая или эллиптическая поляризация). Напомним, что в плоскости фокуса свет в каждой точке имеет только линейную поляризацию, так как при z =0 продольная компонента СУМ S z в (9) равна нулю. Заметим также, что продольная компонента СУМ в точности равна третьей компоненте вектора Стокса:
Sz = 2Im (Ex* Ey ) = 5 3,
которая показывает наличие в световом поле круговой и эллиптической поляризации. В следующем параграфе приведенные здесь теоретические предсказания будут подтверждены с помощью моделирования.
Моделирование по формулам Ричардса–Вольфа
В данном параграфе с помощью формул Ричардса–Вольфа моделировалась фокусировка линейно-поляризованной плоской волны (длина волны – 633 нм) объективом с NA = 0,95. Поле вблизи острого фокуса рассчитывалось с помощью интегралов [1]:
a max 2 n
U(p,Ф,z) = -if J JB(9,ф)T(9)P(9,V)x
Л 0 0 (12)
x exp{ik[psin9cos(ф-ф) + zcos9^} sin 9 d9 dф, где U(p, v, z) — напряжённость электрического или магнитного поля, B (9, ф) - электрическое или магнитное поле на входе широкоапертурной системы в координатах выходного зрачка (9 - полярный угол, ф - азимутальный), T(9) - функция аподизации линзы, f -фокусное расстояние, к=2п / X - волновое число, X -длина волны (в моделировании считалась равной 633 нм), amax - максимальный полярный угол, определяемый числовой апертурой линзы (NA=sin amax), P (9, ф) – вектор поляризации, для напряжённости электрического и магнитного полей имеющий вид:
P ( 9, ф ) =
1 + cos2 ф( cos 9-1) sin ф cos ф( cos 9-1) - sin 9 cos ф
sin ф cos ф(cos 9-1) 1 + sin2 ф( cos 9-1) - sin 9 sin ф a (9, ф) +
b ( 9, ф ) ,
где a (9, ф) и b (9, ф) - функции, описывающие состояние поляризации x - и y -компонент напряжённостей
фокусируемого пучка. После расчета компонент электрического поля рассчитывалось поведение компонент вектора Стокса вблизи острого фокуса. Компоненты вектора Стокса вычисляются с помощью формул:
5 о = E x E x + E y E *
S 1 = E x E X - E y E *
s 2 = 2Re (EE*),
s з = 2Im (ExE*).
Для оценки относительного вклада отдельных составляющих поляризации удобно пользоваться нормированными на поперечную интенсивность компонентами вектора Стокса: ( S 1 , S 2 , S 3 )=( s 1 / s 0 , s 2 / s 0 , s 3 / s 0 ). Известно, что при фокусировке света линейной поляризации в фокусе наблюдаются все три компоненты напряженности электрического поля [15]. Рис. 1 иллюстрирует распределение суммарной интенсивности и отдельных ее составляющих в фокусе апланатического объектива с NA=0,95 при фокусировке плоской волны с длиной волны 633 нм и поляризацией вдоль оси y .
-1
0,5
-0,5

-1 -0,5 0 0,5 1

0,5
-0,5
-1

-1 -0,5 0 0,5 1

0,8
0,6
0,4
0,2
а)
б)
-1
x, мкм
0,5
-0,5

-1 -0,5 0 0,5 1
x, мкм
0,5
-0,5
-1

-1 -0,5 0 0,5 1

в)
x, мкм г) x, мкм
Рис. 1. Распределение суммарной интенсивности I x + I y + I z (а) и отдельных составляющих интенсивности I x (б), I y (в), I z (г) в плоскости фокуса
Из рис. 1 видно, что основной вклад в формирование фокусного пятна вносит исходная компонента, но значительный вклад начинает вносить и продольная составляющая интенсивности. Компонента, перпендикулярная входной поляризации, присутствует, но достаточно мала, при этом свет в фокусе все еще продолжает оставаться линейно-поляризованным. Заметим, что распределения пол- ной интенсивности в фокусе и интенсивности отдельных компонент на рис. 1 подтверждают теоретические предсказания, которые следуют из выражений (4) и (5).
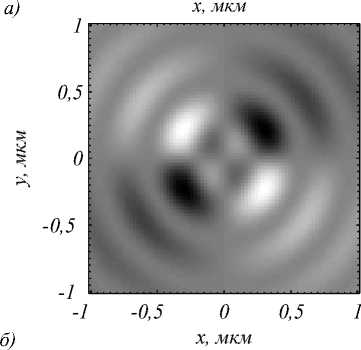
Распределение компонент вектора Стокса ( s 1 , s 2 , s 3 ) и нормированных компонент вектора Стокса ( S 1 , S 2 , S 3 ) на расстоянии z = λ после фокуса показано на рис. 2 и 3 соответственно.
Из рис. 2 и 3 видно, что поляризация после фокуса преимущественно линейна. В центре фокусного пятна на рис. 2 а наблюдается минимум, что говорит о том, что поляризация в фокусе направлена вдоль оси y . Это же подтверждает и рис. 3 а : для волны, полностью поляризованной вдоль оси y , S 1 =– 1. Из рис. 3 а видно, что поляризация не меняет своего направления в фокусе и вдоль осей x и y , а вот вдоль прямых, расположенных под углом ±45° к осям, отклонение от исходной поляризации оказывается максимальным. Из рис. 2 и 3 также видно, что расходящийся пучок содержит области с круговой поляризацией. Напомним, что в самом фокусе таких областей нет – свет линейно поляризован. Из рис. 3 в видно, что вклад круговой поляризации в таких областях достаточно ощутим – при S 3 =± 1 поляризация полностью круговая, здесь же в некоторых областях S 3 достигает значений ± 0,8.
0,5
-0,5

0 0,5 1
-1 -0,5

-2
-4
-6
-8
-10
-1

-1
-2
-3
в
-1
-1
0,5
-0,5

-0,5
0 0,5 1
x, мкм

0,5
-0,5
-1
в)
Рис. 2. Распределение компонент вектора Стокса s 1 (а), s 2 (б) и s 3 (в) на расстоянии λ после фокуса
На рис. 4 аналогично показано распределение нормированного вектора Стокса на расстоянии одной длины волны перед фокусом.
-1
0,5
-0,5

-1 -0,5 0 0,5 1
x, мкм

-0,5
-0,6
-0,7
-0,8
-0,9
а)

0,6
0,4
0,2
-0,2
-0,4
-0,6
-1
-1 -0,5 0 0,5 1
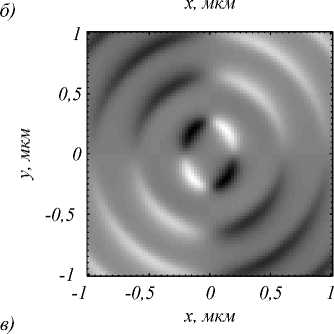
Рис. 3. Распределение компонент нормированного вектора Стокса S 1 (а), S 2 (б) и S 3 (в) на расстоянии λ после фокуса

0,5
-0,5
Из сравнения рис. 3 и 4 видно, что первые две компоненты вектора Стокса, описывающие линейную поляризацию, не поменялись, а третья поменяла знак на противоположный. То есть после прохождения плоскости фокуса направление круговой (эллиптичной) поляризации меняется на противоположную – например, в первой четверти свет перед плоскостью фокуса был с левой круговой поляризацией, а после фокуса – с правой. Наличие правой круговой (эллиптической) поляризации до фокуса во 2-м и 4-м квадрантах, а левой круговой поляризации в 1-м и 3-м квадрантах (рис. 4в) согласуется с теоретическим предсказанием на основе выражения (9). И смена направления вращения вектора поляризации в этих квадрантах после прохождения фокуса также следует из (9). В следующем параграфе для полноты анализа проведено моделирование острой фокусировки света с линейной поляризацией с помощью решения уравнений Максвелла разностным методом.
0,5
-0,5
-1

-1 -0,5 0 0,5 1

-0,5
-0,6
-0,7
-0,8
-0,9
моменты времени. Для расчета комплексной амплитуды на основе отдельных мгновенных значений амплитуд полей использовался метод, предложенный в работе [16]. На рис. 5 показано распределение компонент нормированного вектора Стокса на расстоянии одной длины волны после фокуса.
$i
а)
x, мкм
0,5
-0,5

-1 -0,5 0 0,5 1

0,6
0,4
0,2
-0,2
-0,4
-0,6
-1
-2


0,2
-0,2
-0,4
-0,6
-0,8
-1
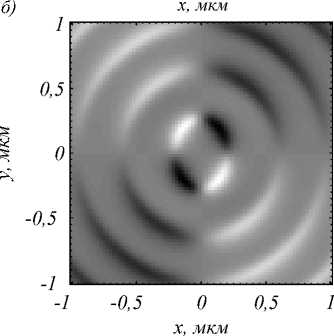
Рис. 4. Распределение компонент нормированного вектора Стокса S1 (а), S2 (б) и S3 (в) на расстоянии λ перед плоскостью фокуса

0,5
-0,5
Моделирование образования круговой поляризации с помощью метода FDTD
Для проверки правильности расчетов по формулам Ричардса–Вольфа было дополнительно сделано моделирование методом FDTD. Рассматривалась фокусировка линейнополяризованной плоской волны (λ = 0,633 мкм) зонной пластинкой Френеля с фокусным расстоянием f =0,5 мкм и диаметром 7,9 мкм. Числовая апертура такой линзы NA=0,99. Моделирование фокусировки осуществлялось с помощью метода FDTD, реализованного в ПО FullWave. Отметим, что метод FDTD, реализованный в FullWave, позволяет рассчитать значения компонент электромагнитного поля в отдельные
б)
-1
-2 -1 0 1 2
а) x, мкм
2 Г
-1
-2


0,5
-0,5
-2 -1 0 1 2
в) x, мкм
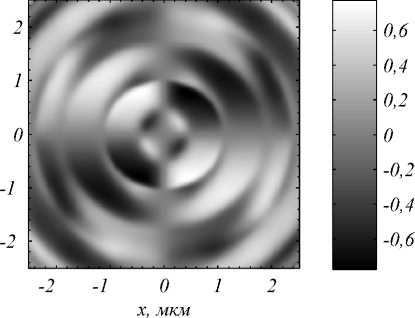
Рис. 5. Компоненты нормированного вектора Стокса S 1 (а), S 2 (б) и S 3 (в) при расчете методом FDTD (ПО FullWAVE) на расстоянии 0,65 мкм после фактического фокуса
Из рис. 5 видно, что моделирование с помощью FDTD-метода подтверждает результаты, полученные с помощью формул Ричардса–Вольфа. В частности, рис. 5 а показывает, что свет преимущественно линейно поляризован вдоль оси y , а рис. 5 в показывает, что квадранты 1 и 3 содержат правую круговую поляризацию, а квадранты 2 и 4 – левую. Аналогичное распределение левой и правой круговой поляризации показано на рис. 3 в .
Уменьшение вклада круговой поляризации при уменьшении числовой апертуры линзы
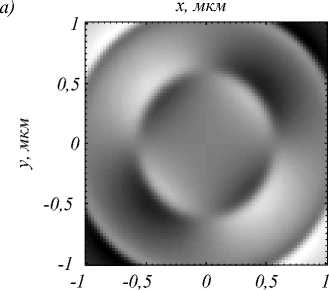
Рассмотрим теперь, к чему приведет уменьшение числовой апертуры линзы до NA=0,6 (соответствует стандартному 40-кратному апланатическому объективу). Результат показан на рис. 6. Из рис. 6 видно, что максимум S 3 уменьшился в 2 раза. А из рис. 6 а видно, что относительный вклад линейной поляризации (вдоль оси y ) значительно вырос: максимум на рис. 3 был равен –0,5, а на рис. 6 а –0,92. Напомним, что при S 1 =± 1 поляризация полностью линейна.
0,5
-0,5

-1 -0,5 0 0,5 1
-1
-0,92
-0,94
-0,96
-0,98
0,2
0,1
-0,1
-0,2
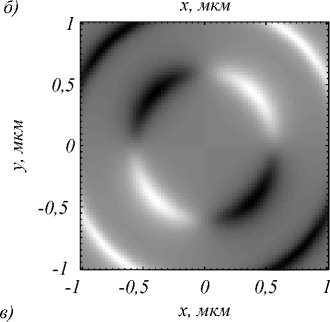
Рис. 6. Распределение компонент нормированного вектора Стокса S 1 (а), S 2 (б) и S 3 (в) при расчете методом FDTD (ПО FullWAVE) для линзы с числовой апертурой NA = 0,6

0,3
0,2
0,1
-0,1
-0,2
-0,3
Заключение
В данной работе теоретически с помощью формализма Ричардса–Вольфа и с помощью двух разных методов моделирования было показано, что при острой фокусировке света с линейной поляризацией в плоскостях до и после фокуса имеют место области, которые возникают парами в четных и нечетных квадрантах и в которых свет имеет круговую или эллиптическую поляризацию (например, в четных правую, а в нечетных левую). Причем после прохождения фокуса в этих областях направление вращения вектора поляризации меняется на противоположенное (в четных квадрантах теперь левая, а в нечетных правая круговая или эллиптическая поляризация). Этот результат позволяет использовать свет с линейной поляризацией для вращения микрочастиц (размер области с круговой поляризацией примерно 0,2 мкм на 0,2 мкм) вокруг своего центра масс.
Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в части «Теоретическое основание», за счет гранта Самарскому университету на реализацию программы стратегического академического лидерства «Приоритет-2030» в части «Моделирование по формулам Ричардса– Вольфа», а также при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части «Моделирование образования круговой поляризации с помощью метода FDTD».
Список литературы Круговая поляризация до и после острого фокуса для света с линейной поляризацией
- Richards B, Wolf E. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc R Soc A 1959; 253(1274): 358-379. DOI: 10.1098/rspa.1959.0200.
- Yuan GH, Wei SB, Yuan X-C. Nondiffracting transversally polarized beam. Opt Lett 2011; 36(17): 34793481. DOI: 10.1364/0L.36.003479.
- Ping C, Liang Ch, Wang F, Cai Y. Radially polarized multi-Gaussian Schell-model beam and its tight focusing properties. Opt Express 2017: 25(26): 32475-32490. DOI: 10.1364/0E.25.032475.
- Grosjean T, Gauthier I. Longitudinally polarized electric and magnetic optical nano-needles of ultra high lengths. Opt Commun 2013; 294: 333-337. DOI: 10.1016/j.optcom.2012.12.032.
- Wang H, Shi L, Lukyanchuk B, Sheppard, C, Chong CT. Creation of a needle of longitudinally polarized light in vacuum using binary optics. Nat Photonics 2008; 2(8): 501-505. DOI: 10.1038/nphoton.2008.127.
- Lin J, Chen R, Jin P, Cada M, Ma Y. Generation of longitudinally polarized optical chain by 4n focusing system. Opt Commun 2015; 340: 69-73. DOI: 10.1016/j.optcom.2014.11.095.
- Zhuang, J, Zhang L, Deng D. Tight-focusing properties of linearly polarized circular Airy Gaussian vortex beam. Opt Lett 2020; 45(2): 296. DOI: 10.1364/OL.45.000296.
- Lyu Y, Man Z, Zhao R, Meng P, Zhang W, Ge X, Fu S. Hybrid polarization induced transverse energy flow. Opt Commun 2021; 485: 126704. DOI: 10.1016/j.optcom.2020.126704.
- Li H, Wang C, Tang M, Li X. Controlled negative energy flow in the focus of a radial polarized optical beam. Opt Express 2020; 28(13): 18607-18615. DOI: 10.1364/OE.391398.
- Kotlyar VV, Stafeev SS, Nalimov AG. Energy backflow in the focus of a light beam with phase or polarization singularity. Phys Rev A 2019; 99(3): 033840. DOI: 10.1103/PhysRevA.99.033840.
- Bomzon Z, Gu M, Shamir J. Angular momentum and geometrical phases in tight-focused circularly polarized plane waves. Appl Phys Lett 2006; 89(24): 241104. DOI: 10.1063/1.2402909.
- Aiello A, Banzer P, Neugebauer M, Leuchs G. From transverse angular momentum to photonic wheels. Nat Photonics 2015; 9(12): 789-795. DOI: 10.1038/nphoton.2015.203.
- Li M, Cai Y, Yan S, Liang Y, Zhang P, Yao B. Orbit-induced localized spin angular momentum in strong focusing of optical vectorial vortex beams. Phys Rev A 2018; 97(5): 053842. DOI: 10.1103/PhysRevA.97.053842.
- Zhao Y, Edgar JS, Jeffries GDM, McGloin D, Chiu DT. Spin-to-orbital angular momentum conversion in a strongly focused optical beam. Phys Rev Lett 2007; 99(7): 073901. DOI: 10.1103/PhysRevLett.99.073901.
- Gross H, Singer W, Totzeck M. Handbook of optical systems; Vol 2. Wiley-VCH; 2005. ISBN: 978-3-52740378-3.
- Golovashkin DL, Kazanskiy NL. Mesh Domain Decomposition in the Finite-Difference Solution of Maxwell's Equations. Optical Memory & Neural Networks (Information Optics) 2009; 18(3). 203-211. DOI: 10.3103/S1060992X09030102.


