Кусочная аппроксимация, основанная на непараметрических алгоритмах моделирования

Введение. В статье рассматривается задача идентификации безынерционных технологических процессов. Схематически, моделируемый процесс отображен на рис. 1 [1]:

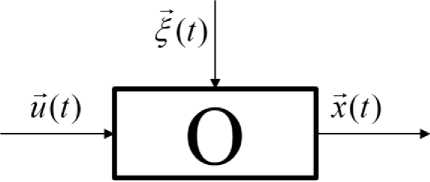
Рис. 1. Моделируемый процесс

Fig. 1. The modelled process

На рис. 1 приняты следующие обозначения: u ( t ) - вектор входных переменных; x ( t ) -вектор выходных переменных; ξ ( t ) – помеховое воздействие; О – процесс.

В качестве основного алгоритма моделирования используется алгоритм непараметрического восстановления функции регрессии [2–5] и кусочно-заданные аппроксимации [6–8].

При получении выборки наблюдений важное значение имеет не только объем выборки наблюдений, но и её качество. Под качеством выборки наблюдений имеется в виду точность считывания параметров, наличие в ней выбросов, равномерность распределения выборки наблюдений и т. д.

Особое внимание уделено проблеме моделирования процесса при неравномерном распределении выборки наблюдений [9–11].

В некоторых задачах выборка наблюдений может быть распределена по области, в которой протекает процесс Q ( u, x ) с разрежённостями, пустотами, скученностью элементов выборки наблюдений. В качестве примера приведем рис. 2, который отражает неравномерно распределенную выборку наблюдений.

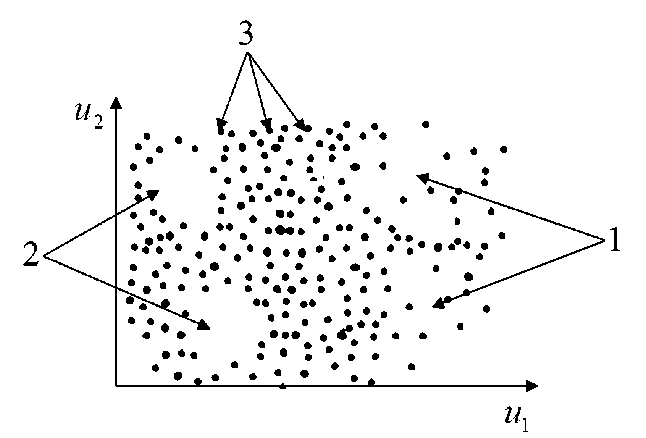
Рис. 2. Неравномерно распределенная выборка наблюдений

Fig. 2. Uneven sample of observations

На рис. 2 в области под номером 1 содержатся так называемые разрежённости в выборках наблюдений, номером 2 обозначены пустоты в пространстве Q ( u, x ) , номером 3 обозначены элементы выборки наблюдений.

Для непараметрической оценки функции регрессии особое значение имеет качество выборки наблюдений. При неравномерном распределении элементов выборки наблюдений возникает сложность в настройке вектора параметров размытости c s , так как в некоторых областях есть разрежённости и предполагается, что в таких случаях c s должен быть большим, а в некоторых областях есть скученности и предполагается, что для этих случаях c s должен принимать малое значение. Безусловно, все это влияет и на качество полученной модели.

Процесс построения математической модели технологического процесса (см. рис. 1) можно условно разделить на несколько последовательных этапов:

• 1)    получение априорной информации о процессе;

• 2)    получение выборки наблюдений;

• 3)    выбор способа построения математической модели;

• 4)    построение математической модели.

В статье уделено внимание этапу выбора способа построения математической модели.

Непараметрическое восстановление функции регрессии. «Параметрический подход» подразумевает, что известна структура исследуемого процесса или объекта, но не известны параметры этой структуры.

От уровня априорной информации зависит вид используемого алгоритма. Если априорной информации достаточно для выбора структуры объекта, то можно использовать параметрические алгоритмы.

Непараметрическая идентификация, в общем виде, реализуется с использованием непараметрической оценки функции регрессии.

sn

Z x- П^ф

' ^us , J    ^UJ , -

x s ( ^u s ) =

1       j = 1

sn

v us, J

cs

— u

j , i

- = 1 J = 1

V     c s    7

В (1) приняты следующие обозначения: Ф(*) – это сглаживающая колоколообразная функция; с s – параметр размытости.

От выбранного параметра размытости сjx напрямую зависит качество построенной модели. Данный коэффициент определяет степень участия элементов выборки в вычислении x в точке uм.

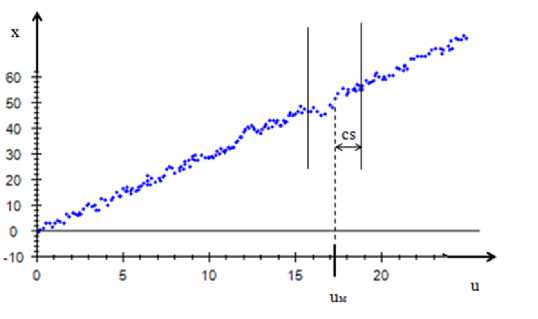
Рис. 3. Определение параметра размытости Fig. 3. Determination of parameter of smooth

Как видно на рис. 3, участвуют в построении модели в точке u м только те переменные, у которых | u – u м | <  c s , притом чем ближе | u – u м | к нулю, тем большее влияние оказывает данная точка на результаты расчетов.

В непараметрической оценке функции регрессии особое значение имеет качество выборки наблюдений. Безусловно, для любой модели качество выборки наблюдений влияет и на точность построенной модели, но в случае непараметрической оценки функции регрессии это имеет особое значение.

Кусочно-заданная аппроксимация Одним из вариантов построения математической модели процесса, идеи которого будут в дальнейшем использоваться, является кусочнозаданная аппроксимация.

Идея кусочно-заданной аппроксимации состоит в том, чтобы разделить область Омега на некоторые подобласти Qz (й), - = 1, m (рис. 4) и для каждой области Qz (й) строить свою математическую модель процесса.

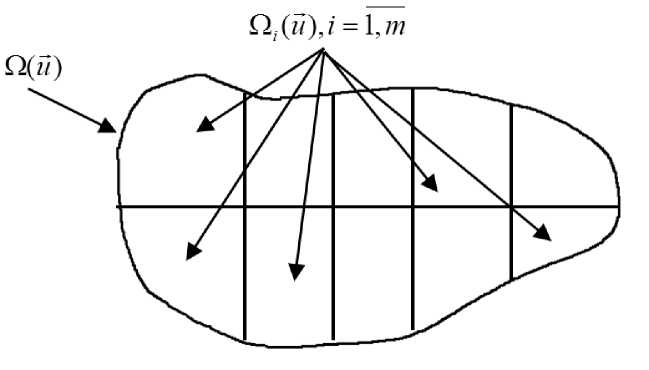
Рис. 4. Разбиение Q ( й) на подобласти Q_z ( и)

Fig. 4. Split Q ( й) into sub-areas Q_z ( Й)

Одними из самых известных кусочно-заданных аппроксимаций являются сплайн-функции. Преимуществом такого подхода является то, что неравномерность выборки наблюдений не имеет большого влияния на качество модели. Слабой стороной сплайн-функций можно признать то, что для задач больших размерностей достаточно сложно подобрать функцию и настроить параметры для каждой области Qz (м) .

Разработанная модификация непараметрической оценки функции регрессии. Сложность непараметрической оценки функции регрессии, в отличие от сплайн-функций, возрастает гораздо медленнее. В связи с этим кажется логичным объединить идею кусочно -заданной аппроксимации и непараметрическую оценку функции регрессии.

Разработана следующая модификация непараметрической оценки функции регрессии.

Этап построения модели:

• 1)    область Омега разделяется на подобласти Q_z ( ^Й ) ;

• 2)    для каждой области Q_z ( Й) производится восстановление функции регрессии при помощи непараметрической оценки функции регрессии ;

• 3)    производится настройка вектора размытости для каждой области Q_z ( й) [12].

Этап построения прогноза в точке й :

• 1)    определяется область Q_z ( I^й) , к которой принадлежит точка й ;

• 2)    производится восстановление функции регрессии с использованием настроенного вектора параметров размытости для области Q_z ( I^й) .

Подобласти Q_z ( I^й) могут быть разделены различными методами, можно применить и алгоритмы разбиения выборок по классам либо выбрать классический путь для сплайнов и разбить всю область определения входных переменных на равные части и производить настройку вектора параметров размытости для каждого из них.

Вычислительные эксперименты. Проведены численные эксперименты по сравнению классической непараметрической оценки функции регрессии с предложенной модификацией. Численные эксперименты проводились для нескольких случаев, отличающихся по неравномерности распределения компонентов выборок наблюдений.

В первую очередь проведен эксперимент по моделированию объектом, описываемым следующим уравнением:

f ( 1^й) = f ( u , u ₂, u ₃, u ₄, u ₅, u ₆) = 6sin( u ) + 2 u ₂ + й ₃/6 + 4cos( й ₄) + й ₅ - 8 й _б.    (2)

Сразу отметим, что алгоритму восстановления функции регрессии не известен вид уравнения. Уравнение используется только для генерации выборки наблюдений.

Приняты следующие исходные данные для проведения эксперимента: размер выборки наблюдений s =   4000; величина помехи, воздействующей на объект

• § = 4%; u e (0;3); элементы выборки наблюдений распределены равномерно.

Модель будет построена при помощи алгоритма непараметрической оценки функции регрессии и при помощи предложенной модификации алгоритма.

Результаты моделирования представлены в табл. 1

Таблица 1

Результаты восстановления функции регрессии

	Непараметрический алгоритм восстановления функции регрессии	Модифицированный непараметрический алгоритм восстановления функции регрессии
Средняя ошибка прогноза, %	3	4
Время настройки параметров размытости, мс	30	70
Скорость дачи прогноза, мс	45	69

По результатам проведенного эксперимента видно, что средняя ошибка прогноза в модифицированном алгоритме незначительно уменьшилась, также увеличилось время настройки параметров размытости и скорость дачи прогноза.

Этот эксперимент продемонстрировал, что в случае равномерного распределения выборки наблюдений нет необходимости разбивать элементы выборки наблюдений на классы. Тут же хотелось бы отметить, что рассмотренный случай встречается на практике довольно редко. Выборка почти всегда имеет сгущенности или разрежённости.

В следующем численном эксперименте выборки наблюдений будут иметь разрежённости и сгущенности элементов.

Результаты моделирования объекта в таких условиях сведены в табл. 2.

Таблица 2

Результаты восстановления функции регрессии в условиях разрежённости и сгущенности элементов выборки наблюдений

	Непараметрический алгоритм восстановления функции регрессии	Модифицированный непараметрический алгоритм восстановления функции регрессии
Средняя ошибка прогноза, %	14	7
Время настройки параметров размытости, мс	35	70
Скорость дачи прогноза, мс	52	84

Согласно проведенному эксперименту разница между средней ошибкой моделирования классического алгоритма непараметрической оценки функции регрессии и предложенной модификации выше, чем в эксперименте, отображенном в табл. 1. Исходя из этого, можно заключить, что при появлении неоднородности в выборке наблюдений, предложенная модификация позволяет точнее построить оценку функции регрессии.

Для подтверждения этого предположения проведен ещё один эксперимент, в котором введена ещё большая неоднородность в выборке наблюдения, чем в эксперименте, отображенном в табл. 2.

Результаты этого эксперимента сведены в табл. 3.

Таблица 3

Результаты восстановления функции регрессии в условиях большей неоднородности в выборке наблюдений

	Непараметрический алгоритм восстановления функции регрессии	Модифицированный непараметрический алгоритм восстановления функции регрессии
Средняя ошибка прогноза, %	23	8
Время настройки параметров размытости, мс	36	69
Скорость дачи прогноза, мс	49	78

Как можно заключить из табл. 3, при увеличении неравномерности распределения элементов выборки наблюдений, точность предложенной модификации становится выше точности классического алгоритма.

Важно отметить, что неравномерность в выборке наблюдений повсеместно встречается при моделировании объектов с большой размерностью входных-выходных переменных.

Заключение Разработана модификация алгоритма непараметрического восстановления функции регрессии. Модификация заключается в использовании идеи кусочно-заданных аппроксимаций и разбиении области моделирования на подобласти, для каждой из которых отдельно восстанавливается функция регрессии.

В ходе вычислительных экспериментов продемонстрировано, что предложенная модификация существенно улучшает качество моделирования процесса, когда элементы выборки наблюдений распределены неравномерно, имеются разрежённости и пустоты в выборке наблюдений. Важно отметить, что существуют и другие методы борьбы с неравномерно-распределенной выборкой наблюдений [13–15].

Acknowledgment. This work was financially supported by the Ministry of Science and Higher Education of the Russian Federation in the implementation of the integrated project “Creation of a production of earth stations of advanced satellite communications systems to ensure the coherence of hard, northern and Arctic territory of Russian Federation”, implemented with the participation of the Siberian Federal University (agreement number 075-11-2019-078 dated 13.12.2019).