Квалиметрическая модель интегральной оценки безопасности функционирования военно-технических систем

Таблица 1. Требования к интегральной квалиметрической оценке

№ п/п	Требование к интегральной оценке	Формула	Комментарий
1	Коммутативность (равноценность)	d(d 1 , d 2 )=d(d 2 , d 1 )	Одинаковая важность частных оценок d1 и d2, т.е. интегральная оценка не зависит от порядка частных оценок, а зависит от всего их множества
2	Ассоциативность (иерархическая одноуровненность)	d(d(d 1 , d 2 ), d 3 )= =d(d 1 , d(d 2 , d 3 ))	Агрегируются лишь частные оценки d j , принадлежащие одному уровню иерархической структуры – «дерева» качеств функционирования ВТС
3	Гладкость	d(d1, d2) – многочлен	Это требование непрерывной зависимости интегральной оценки от частных оценок
4	Ограниченность	0 ≤ d(d 1 , d 2 ) ≤ 1 при 0 ≤ d 1 , d 2 ≤ 1	В квалиметрии задаются или предполагаются известными границы интервала изменения частных и интегральной оценок
5	Нейтральность	d(d 1 , 0)=d 1 , d(0, d 2 )=d 2 ; d(0, 0)=0, d(1, 1)=1	Интегральная оценка совпадает с частной оценкой, когда другая оценка принимает минимальное значение

В работе [1] сформулирована следующая теорема. В классе многочленов двух переменных существует лишь три (с точностью до постоянных параметров) функции, удовлетворяющие условиям коммутативности и ассоциативности. Эти функции имеют вид:

• 1)    с;(1)

• 2)    d1+ d2 + c;(2)

• 3)    a(d1+ d2) + bd1d2 + a(a – 1)/b,(3)

где a, b, c – произвольные константы, b ≠ 0.

Доказательство теоремы основано на представлении функции d(d1, d2) в виде двойного степенного выражения с учетом, которое подставляется в условие ассоциативности. Учет аксиомы коммутативности и сравнение коэффициентов в обеих частях равенства приводят к функциям (1)-(3).

Оценка вида (1) тривиальна из-за независимости интегральной квалиметрической оценки от частных оценок. Вид (2) соответствует аддитивной свертке. Оценка вида 3) не может быть сведена к виду (1) или (2), так как b≠0.

Следствие 1. Многочлен f(d 1 , d 2 ), удовлетворяющий свойствам ассоциативности, коммутативности и ограниченности (см. табл. 1), представим в виде

• 1)    d 1 + d 2 – d 1 d 2 ;

• 2)    d 1 d 2 .

Предположим, что d1 и d2 ϵ [q, Q] и требуется, чтобы d(d1, d2) ϵ [q, Q], причем d(q, q) = q и d(Q, Q) = Q.

Таблица 2. Основные виды ассоциативных интегральных квалиметрических оценок

Аксиомы				Вид интегральной оценки d(d i , d2)	Комментарии
коммутативность	гладкость	ограниченность	нейтральность
+	–	–	–	Ф-1(Ф(d 1 )+Ф(d 2 ))	φ – произвольная строго монотонная функция. Например, при φ(x)=x и φ(x)=ln(x) имеем аддитивную и мультипликативную интегральные оценки
+	–	–	+	ф-1(ф(d 1 )+ф(d 2 ))	φ – монотонная непрерывная функция. Из аксиомы нейтральности следует: Ф(d 1 mln) = ф(d 2 mln) = 0
+	+	–	–	1)    с; 2)    d , +d 2 +c; 3)    a(d i +d 2 )+bd i d 2 + +a(a–1)/b	a, b ≠ 0, c – произвольные константы
+	+	+	–	1)    d1+d 2 —d1d 2 2)    d 1 d 2	Оценки d1, d2 и d принимают значения из интервала [0,1]. Интегральная оценка 1) имеет смысл риска недостижения требуемого качества функционирования системы
+	+	+	+	d i +d 2 -d i d 2	Аналог вероятностной свертки для двух совместных независимых событий

Запишем данные требования в виде системы уравнений

f(q, q) = q f(Q, Q) = Q"

С учетом общего вида коммутативного, ассоциативного многочлена, полученного из теоремы, система примет следующий вид:

^2aq + Ь, - + а⁽а - 1)/Ь = ^q

^2aQ + b^{Q -} + ’(a — ^1)/Ь = ^Q

Из данной системы получаем следующее уравнение относительно a:

2a(Q - q) + b(Q - q)(Q + q) = Q - q.

Поскольку Q - q + 0, то 2a + b(Q + q) = 1. Следовательно, a = [1-b(Q+q)]/2.

Подставим значение а, выраженное через b, в первое уравнение системы, получим:

q[1 - b(Q + q)] + bq ² - [1 - b ² (Q + q) ² ]/4b = q.

Выполнив преобразования, получим следующее уравнение: b²(Q - q)² = 1, откуда и b = ±1 / (Q - q). Подставив значения b в выражение (4), получим соответствующие значения а. Таким образом, найдены два набора коэффициентов a и b: a′ = –q/(Q–q), b′ = 1/(Q–q) и a″ = Q/(Q–q), b" = -1/(Q-q), а следовательно, и два вида зависимости f(d i , d₂):

d‘=a‘(d₁+d 2 )+b‘d₁d 2 +a‘(a‘-1)/b‘=[-q/(Q-q)](d₁+d 2 )+[1/(Q-q)]d₁d 2 + +[-q/(Q-q)][-q/(Q-q)-1]/[1/(Q-q)]=

= 1/(Q-q)[-q(d1+d2)+d1d2+Qq], d"=a"(d1+d2)+b"d1d2+a"(a"-1)/b"=[Q/(Q-q)](d1+d2)+ +[-1/(Q-q)]d1d2+[Q/(Q-q)][Q/(Q-q)-1]/[-1/(Q-q)]= = 1/(Q-q)[Q(d1+d2)-d1d2+Qq].

Если q = 0 и Q = 1, то db d2, f(d1, d2) □ [0, 1]. В этом случае d‘= d1d2, d" = d1+d2-d1d2. Что и требовалось показать.

Следствие 2. Многочлен f(db d2), удовлетворяющий свойствам ассоциативности, коммутативности, ограниченности и нейтральности (см. табл. 1), представим в виде d= d1 +d2 -d1d2 =1-(1-d1)(1-d2).                                                      (5)

Отметим, что формула (5) совпадает с формулой вероятности суммы двух совместных независимых событий. (Вероятность суммы двух совместных событий A и B вычисляется по формуле P(A+B) = P(A) + P(B) – P(AB), а P(AB)= P(A) P(B) для независимых событий.)

Для построения интегральной квалиметрической оценки d нужно иметь частные относительные квалиметрические оценки dj функционирования ВТС по j-му ПК, j=1,2,^,m. Обозначим через Yj1 - значение j-го ПК для i-го состояния ВТС, а через yj* - пороговое (предельно допустимое) значение, отражающее нормативное требование к качеству функционирования ВТС по j-му ПК. Поставим им в соответствие две безразмерные величины, принимающие значения из интервала [0,1]: pj^ijyj - абсолютную частную оценку качества и Ej=Ej(y*j) - соответствующий нормативный уровень по j-му ПК. Будем считать, что требование к качеству функционирования ВТС (например, требование к экологической безопасности района базирования) по j-му ПК выполнено, если Ц|‘>£|. При этом частная оценка dj, как функция величин Ej и gj, должна удовлетворять следующим условиям: 1) 0< dj <1 при p.j>Ej; 2) dj=0 при Ej=0, gj>0 (оценка минимальна, если нет никаких требований к качеству); 3) dj=0 при gj=1 и gj>Ej (оценка минимальна при «идеальном» качестве независимо от требований); 4) dj=1 при gj=Ej*0 (оценка максимальна при предельно низком допустимом качестве). В работах [1-4] показано, что при p.j>Ej условиям 1)-4) удовлетворяет частная квалиметрическая оценка dj вида dj=[Ej(1-№)]/[qj(1-Ej)].                                                                     (6)

Покажем, что данная оценка позволяет вычислять условную вероятность события, состоящего в том, что требование к интегральному качеству функционирования ВТС не выпол-– 239 – няется при выполнении требований к ее качеству по j-му частному ПК. Обозначим через µ интегральное качество (качество в целом) функционирования ВТС, а через ε – требование к этому качеству. Будем считать, что требование к интегральному качеству функционирования ВТС выполнено, если µ≥ε. Причем если качество µ функционирования ВТС хотя бы по одному ПК ниже соответствующего нормативного уровня ε , то удовлетворить требование к ин-j тегральному качеству функционирования ВТС невозможно. Пусть А – событие, состоящее в том, что не выполнено требование к интегральному качеству, а Bj – событие, состоящее в том, что не выполнено требование к качеству функционирования ВТС по j-му ПК. Тогда условная вероятность P(A|Bj) = 1, так как если ц,<е,,то ц<б. В то же время 0

P(A| B j ) = {P(B j )[1 - P(B j | A)]}/{P(B j | A)[1 - P(B j )]}.                         (7)

J J J _ J J

Введем следующие обозначения: d j =P(A|B j ), ε j =Р(B j ) – вероятность некачественности функционирования ВТС по j-му ПК, µ j =Р(В j |А) – вероятность некачественности функционирования ВТС по j-му ПК при условии, что требования к качеству функционирования ВТС не выполнены. В результате получаем, что формула (7) совпадает с формулой (6) частной относительной оценки d j типа «риск недостижения требуемого качества функционирования ВТС», которая является квалиметрической моделью частной относительной оценки опасности функционирования ВТС. В силу вероятностной природы величин d j , ε j , µ j они принимают значения из интервала [0,1]. Причем, µ j ≥ε j .

Доопределим оценку d j следующим образом: 1) d j =1 при µ j = ε j =1; 2) d j =0 при µ j = ε j =0; 3) d j =1 для всех µ j < ε j . Отметим, что оценка d j является убывающей функцией по µ j и возрастающей по «,

В общем случае для m частных оценок интегральная квалиметрическая оценка функционирования ВТС имеет следующую структуру [1]:

d = 1 -]П (1 - d j ).                                                              (8)

Операцию, задаваемую функцией вида (1), будем называть обобщенным сложением (квазисложением) и обозначать символом ⊕ : d=d₁ ⊕ d₂. Эта операция обладает всеми свойствами обычной операции сложения. Можно показать [1], что операция обобщенного умножения на произвольное неотрицательное число λ , которую обозначим символом ⊗ , может быть введена в форме

λ j ⊗ d j =1-(1-d j ) ^{λ j}.                                                                     (9)

Данная операция согласована с операцией квазисложения и удовлетворяет соотношениям вида: 1 ® d_J=d_J, X o ® (d i ® d 2 )= X o ® d i ®X o ® d 2 , ( Х^Х г ) ® d_J= X i ® d_J ®X 2 ® d_J.

Подчеркнем, что формула (8) интегральной квалиметрической оценки получена в предположении коммутативности (равноценности) и ассоциативности (иерархической одноуров-ненности) частных оценок. Использование весовых коэффициентов X для «выравнивания» значимости частных квалиметрических оценок dj само по себе противоречиво. Аксиома коммутативности уже предполагает равноценность этих оценок. Такого рода «равноправность» достигается единым способом измерения частных абсолютных оценок качества ц и норматив^ных уровней S ^J.

Поэтому некоммутативная аддитивная линейная свертка оценок d₁ и d₂ вида X ₁d₁+ X ₂d₂ становится коммутативной для величин d'₁= X ₁d₁ и d'₂= X ₂d₂. Рассмотрим конкретные способы «выравнивания» частных оценок d , .

Из формул (6) и (9) для Х >0 имеем:

[ _S ' j (1^ )]/[ ц ' , (^' j )].= (_S>' j ^j )/(1- _S ' j ) = d’ J = X j ® d = 1-(1-d ) ^A .

Покажем, что здесь e'j=1-(1-ej)Xj, цх=[1-(1-е,)Xj]/[1-(1-Ej/ц)Xj]. Действительно, d’=[H1jj)Xj-t+(t-ejM1-ej)Xj=1^^            =1-[(1-4Г.

Таким образом, в общем случае интегральной квалиметрической оценке типа «общий риск недостижения требуемого качества функционирования ВТС» соответствует квалиметри-ческая модель вида d = 1 -fl(1 -dj)z,                                                (to)

^{J = 1}

где X j - весовые коэффициенты частных оценок d_p удовлетворяющие условию нормировки:

m

$ ^=1,^>0,а=1,2,^,т.

Подчеркнем, что интегральная квалиметрическая оценка d в формуле (10) при λ = 1/m является средней величиной в смысле ассоциативной средней по Колмогорову [5], которая вычисляется по формуле

( 1             11

d(di ,d2,...,dm) = ф 11 — ф^) +—ф(^) +... +—ф(^) ^m    mm

Здесь ф - непрерывная строго монотонная функция, а ф-1 - функция, обратная к ней. В нашем случае φ(d) = -ln(1-d). При φ(d) = ln d имеем среднюю геометрическую. Так, в работе Э. Харрингтона [6] частными оценками качества системы являются экспоненциальные функции «желательности», а интегральная оценка есть среднее геометрическое этих частных оценок. В то же время средняя квазигеометрическая величина d в формуле (8) не средняя величина по Коши [5], т.е. не удовлетворяет условию min(dbd2) < d < max(dbd2). Покажем, что средневзвешенное квазигеометрическое есть среднее по Коши. В силу коммутативности квалиме- трической оценки d рассмотрим только случай dt > d2. Так как min(dbd2) = d2, max(dbd2) = dt то имеем:

1 - (1 - di) "(1 — d2) "2 < 1 — (1 — d^)"1 (1 — dj"2 = d = тах(4Д), l-^-d./^l-doy2 > 1 -(1 -d2)^(l-d2)^ = d2 =min(d„d2).

Таким образом, min(d 1 ,d₂) <  1 — (1 — d i ) ^ — d 2 ) ^ <  max(d i ,d 2 ) и средневзвешенное квази- 12        1      2         12

геометрическое d есть среднее по Коши.

Приведем геометрическую интерпретацию квалиметрических оценок. «Отрезок» d = A ® d ¹ © (1 - 2 ) ® d ² (0<^<1), соединяющий две точки d ¹=(d 1i ,d 12 ) и d ²=(d 2i ,d 22 ) в про^{странстве} частных ^{квалиметрически}х оценок, показан ^на рис. 1. Средневзвешенной ^арифметической величине соответствует отрезок прямой d a = 2 d ¹ + (1 - 2 )d ² , а средневзвешенной геометрической - «отрезок» d g = _W ( d ² )^- '

Подчеркнем, что с теоретико-информационной точки зрения [7, с. 38] число фй) = -ln(1-dj) является мерой неопределенности информации (частной информационной оценкой) при вычислении энтропии события, так как частную квалиметрическую оценку dj можно интерпретировать как вероятность Р( A | Bj) события A, состоящего в том, что не выполнено требование к интегральному качеству функционирования ВТС, при условии, что выполняется событие B , 1 состоящее в том, что требование к качеству функционирования ВТС по j-му ПК выполнено [1]. Таким образом, событию (A| Bj) соответствует неопределенность, равная -ln[P( A | Bj)] = ln[1/P( A | B )], а противоположному событию (A | B ) - частная информационная оценка |=|(dj)= -ln[P( A | Bj )]=ln[1/(1-P( A | Bj )]=ln[1/(1-dj)]. Укажем основные свойства оценок Т,: 1) Ij=0 при dj =0; 2) Ij ^» при dj ^1.

m

Отметим, что интегральная информационная оценка I=I(d)= ln[1/(1-d)]=^AjIj есть j=1

средневзвешенная арифметическая величина, которая является функцией средневзвешенного «квазигеометрического» - интегральной квалиметрической оценки d, соответствующей формуле (10). Можно показать, что величина I=-ln(1–d) – «квазисредняя» величина

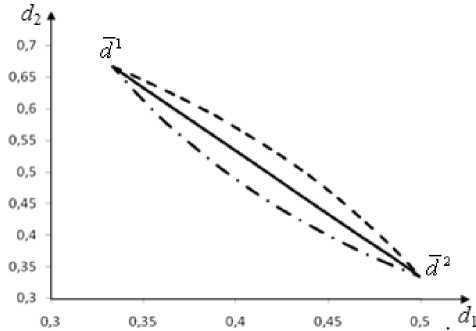
Рис. 1. Графическое представление средневзвешенных величин:

– геометрическое

– арифметическое;

– квазигеометрическое;

(длина в натурально-логарифмической шкале), обеспечивающая минимум «квазидиспер- сии»:

/

S d = z л ln j ¹ X

1 ^ ²

In----

¹ - d j      ¹ - ^d J

= £ A j [ ln(1 - d j ) - ln(1 - d) ] 2 . j = i

Для двух частных квалиметрических оценок d 1 и d 2 с весовыми коэффициентами λ 1 и λ 2 соответственно имеем:

S d = λ 1 (ln(1-d 1 )-ln(1-d))² + λ 2 (ln(1-d 2 )-ln(1-d))² =

= (λ 1 +λ 2 )[ln(1-d)]² – 2(λ 1 ln(1-d 1 )+λ 2 ln(1-d 2 )) ln(1-d) + λ 1 (ln(1-d 1 ))² + λ 2 (ln(1-d 2 ))².

Из условия оптимальности следует, что ln(1-d) = (λ₁ln(1-d₁) + λ₂ln(1-d₂)) / (λ₁ + λ₂). Значит, d=1-(1-d 1 ) ^{λ 1}(1-d 2 ) ^{λ 2}. В общем случае для m частных оценок d j получаем формулу (10).

На этом этапе формирование интегральной квалиметрической оценки можно было бы считать завершенным, но обычно полученные величины I модифицируются. Дело в том, что частная квалиметрическая оценка dj и частная информационная оценка Ij устроены так, что и «улучшение» качества функционирования ВТС совпадает с уменьшением значений dj и Ij . Традиционно принят обратный («зеркальный») счет. Зададимся некоторой величиной de такой, что

I j

= In

¹ d e

- In

1 — ¹ - d j

= In

1-d j

1 - d_e

= In

^{1 - d} e

I j .

Если за d e взять величину

d_e = 1 — « 0.63, то e

ln------ = 1 , а I

1 - d e

j = 1 + ln(1 - d j ), тогда

mm        m         m       m

I - Z ^ + Z ^ , ln(i - d j ) - ¹ + 2 a , in(i - d j ) = ¹ - z ^ j ln— = ¹ - Z ^ I j = ¹ - 1.

J = 1         j - ¹                               j - ¹                                 j - 1           ^{1 -} d j           j - 1

Для содержательной интерпретации квалиметрических оценок функционирования ВТС предлагается использовать зеркальную вербально-числовую шкалу Харрингтона [5], для которой величина d e =1-1/e ≈0.63 является особой точкой – точкой перехода системы в «некачественное» состояние.

Если величины d j рассматривать как риски (вероятности) недостижения требуемого качества функционирования ВТС по j-му ПК (j-му потребляемому ресурсу), то оценки I(d j ) отражают информацию о значимости ПК (о степени дефицитности ресурсов по качеству). Причем чем больше значение I(d j ), тем больше чувствительность управленческих решений к изменению квалиметрической оценки d j (изменению качества j-го ресурса) для достижения качества функционирования ВТС. Это позволяет рассматривать I(d j ) как своего рода универсальные стоимостные измерители единицы j-го ресурса и использовать их в роли коэффициентов информационной линейной целевой функции типа обобщенных затрат в моделях многокритериальной ресурсной оптимизации сложной системы [1]. Данная целевая функция стимулирует эффективное использование дефицитных по качеству ресурсов в процессе функционирования ВТС.

Покажем, что интегральные оценки di можно применять в системах мониторинга управления функционированием, а именно для оценки изменений качества функционирования ВТС с учетом дополнительной информации (наблюдений) о состоянии «новых» систем. Пусть сред-– 243 – ствами мониторинга получены L «новых» наблюдений, которым соответствуют значения yji показателей качества, j = 1, 2, ..., m; i = N+1, N+2, ..., N+L. Таким образом, к первоначальному списку N состояний систем добавилось L «новых» с тем же набором ПК (по наименованиям и количеству). Необходимо упорядочить весь имеющийся список N+L систем по уровню качества функционирования с учётом ранжировки первоначального списка ВТС. Если в «первоначальном» ранжировании одна ВТС лучше другой (или они эквивалентны) в смысле качества функционирования, то добавление новых систем не должно изменить уже имеющееся отношение предпочтительности (эквивалентности). Таким образом, требуется определить интегральные квалиметрические оценки с учетом новой информации о состоянии функционирования ВТС на фоне ранжировки первоначальных систем.

Будем считать, что с появлением новой информации может изменяться исходная экспертная информация, необходимая для построения интегральной квалиметрической оценки. А именно:

• 1)    заданы новые интервалы изменения j-го ПК – [A j , B j ], где A j ≤ a j и B j ≥ b j ;

• 2)    заданы новые предельно допустимые значения и новые нормативные уровни – Y^*, E . jj

Предполагается, что для каждого ПК остаются без изменения способ нормировки (см. , табл. 2) и значения весовых коэффициентов Xj частных оценок dj. Для всего списка (N+L) систем с учетом новой информации частная абсолютная квалиметрическая оценка Mji по j-му ПК для i-го состояния ВТС имеет вид, аналогичный виду μi (см. табл. 2): Mi = Mi(yi, A B ). Частная относительная D i по j-му ПК и интегральная Di квалиметрические оценки для i-го состояния j

ВТС вычисляются по формулам

D j = [E j (1 - M i )]/[M i (1 — E j )] ,

m

D ' = 1 - П (1 - D J ) \i = ^{1 , 2 ,}...^{, N} + L; J = 1 , 2 ,..., m -                      (13)

• j ¹

При этом ранжировки первоначального списка N систем по значениям Di и di будут отличаться друг от друга.

Утверждение. Существуют преобразования квалиметрических оценок, которые позволяют произвести упорядочение всех анализируемых систем, сохраняющее отношения предпочтительности (эквивалентности) в первоначальном списке при получении новой информа- ции.

Доказательство. Для включения новых ВТС в ранжировку первоначального списка по значениям dⁱ необходимо «скорректировать» значения величин M j ⁱ с помощью преобразования _i

M i = F ( M i ) . При этом значения частной относительной D j и интегральной D i квалиметриче-ских оценок вычисляются по формулам

^D = [ j - M)]/^ -                           (14)

• ^D = ¹ — ^{П (1 - D j )} .                                                   ⁽¹⁵⁾

Эти оценки обладают следующими свойствами: 1) если d i > d¹, то и D i > D l ; 2) если d i = d¹, то и ID i = D l , i, l = 1, 2, ..., N.

Неравенство di ≥ d1 перепишем в виде mm

1 - п (1 - d i )¹ - П (1 - d i ) j                                       (16)

".,                                   , . 1

Вначале рассмотрим случай, когда изменение состояния системы рассматривается лишь с точки зрения «корректировки» одной частной квалиметрической оценки d j . Без ограничения общности можно считать, что это оценка d₁. Тогда неравенство (7) перепишется следующим образом:

• (1 - d¹)о ^- d¹) чй» - d i ) ■ / П ⁽1 - d l ) ].                        ⁽¹⁷⁾

Введем в рассмотрение величину D'=ft

• ^{1    -} d = 1 - j - Р_Ж ⁽1 ^{- E} j ) p ' ^] = fr.^j- _Ej_№^j (. - j j = [1 - j^ц_№ - . , ] , то неравенство (17) будет иметь вид

• 1    -E l / ц , >  D\i -E l / H i ).                                                   (18)

Обозначим через    z^ = ¹ - E i / ц ¹ , z/ = 1 - E i / H l ; Z i = ¹ - E i ^{/M ,} ; Z i = ¹ - E i /M i ;

Z =1 - Bi /М-; Zi =1 - Bi /Mj. Тогда неравенство (10) будет       ид z, > ^ Необхо димо показать, что из условия zi > D zi следует неравенство Z, > D Z,. Таким образом, дока-зателвство утверждения сводится к поиску преобразования Z ф. я, такого, что из выполнения l il i                                                    l il i неравенства z, > D z, следует, что ф(z1) > D ф(z1).

Вначале найдем решение следующего функционального уравнения относительно неиз-^,ест"^ой функции ^{ф :}

= D C ...)                                                                              (19)

Учитывая, что z¹ = Dⁱ¹zⁱ, имеем ф (Dⁱ¹z) = Dⁱ¹ ф (z). Будем искать решение уравнения (19) в классе непрерывно дифференцируемых функций. Продифференцируем обе части последнего уравнения по z: Dⁱ¹ ф'( D i' z) = Dⁱ¹ ф' (z). Т.к. D i ¹ + 0, то ф ( D i1 z) = ф (z). Введем обозначение g(z) = ф (z). Тогда для любого D i* > 0 имеет место следующее функциональное уравнение: g ( Dz) = g(z). При Dⁱ¹< 1 g(x) = g(Dⁱ¹ x) = g[(Dⁱ¹)²x] = ... = g[(Dⁱ¹)ⁿx]. Перейдя к пределу при n→∞, получим g^(z) = g⁽⁰⁾ = const. Пусть g^(z) = y, т.е.^ф'^(z) = Y Поэтому ^{ф (z)} = Yz + (3, где Y,^e = const. Отделим ^значения констант y и в. Так как z , = D il z , , то y z , +в= ф ( _z l ) = D i¹ ф (. , ) = D i¹ ( y z , + в ) = D i¹ y z , + D i¹ в . i i

При этом y z, + ^e = y D z i +^в , тогда ^в = D i1 ^e для любого D i ¹. Следовательно, ^в l = 0 и ^ф^ ) = ^Yz, а решением уравнения ^{(19) п}ри Y ^ 0 ^{является} функция ^{ф (z)} = Yz. Поскольку z i >  D z i , D i ¹ > 0, то для любого Y > 0 выполняется неравенство y z | > y D il z j , которое можно переписать в виде _t (z i ) > D4(z_;). Отсюда следует, что ^= или 1 - В,^ ..( . -./, ).

Так, скорректированная абсолютная оценка качества M ⁱ для i-го состояния ВТС вычисляется по следующей формуле:

M, 1 = E ,-„-. 1 . 1,

Таким же образом осуществляется корректировка остальных частных абсолютных оценок качества. В табл. 3 даны формулы корректировки для некоторых видов этих оценок.

Таблица 3. Формулы корректировки частых абсолютных квалиметрических оценок

Номер п/п	Способы нормировки	Скорректированная абсолютная оценка
1	i a j       i A j и ' " y j ’    ' " y i	M i = E j /[1 - Y j ( l - e j /Cp j M J ) ) ], где p = a /A, 0<γ ≤[1 – E] / [1 – ε A / a]
2	i b j - y j M-    B j - y i .4J              ’M J = b j - a i          b j - a j	М- = Е/[1 - ^ ( 1 - ^ /(рМ + q) ) ], где p=(B -A)/(b-a), q=(b-B)/(b-a), 0 j < [l - E j ]/[1 -8 j (b j - a j )/(b j - A j )]
3	i в                           i iP j - - b j - y j    ui - b j - y j Ц J [ b j - a j j ’ J [ B J - A j ]	M i = E j /[l - Y j ( 1 - 8 j /[P j (M i )1/k + q j ]k ) ], где p=(B - A)/(b - a), q=(b - B)/(b - a), 0<γ ≤[1 - E] / [1 - ε (p+ q)k]

Таблица 4. Показатели шума, абсолютные оценки качества окружающей среды, относительные и интегральная оценки акустической дискомфортности первоначального списка объектов шумового мониторинга

Номер п/п	y 1	y 2	μ 1	μ 2	d 1	d 2	d	Ранг
1	94	75	0,310	0,255	0,176	0,245	0,212	8
2	56	48	0,953	0,939	0,004	0,005	0,005	1
3	82	70	0,513	0,381	0,075	0,136	0,106	5
4	89	76	0,395	0,229	0,122	0,281	0,206	7
5	92	81	0,344	0,103	0,151	0,732	0,523	9
6	98	71	0,243	0,356	0,248	0,151	0,201	6
7	87	50	0,429	0,888	0,106	0,011	0,059	2
8	88	54	0,412	0,787	0,113	0,023	0,069	4
9	107	73	0,090	0,305	0,798	0,191	0,596	10
10	88	53	0,412	0,812	0,113	0,019	0,068	3

Покажем применение интегральных оценок di для оценки изменения качества (техногенной безопасности) функционирования ВТС с учетом дополнительной информации (наблюдений) о состоянии «новых» систем на примере мониторинга шумового загрязнения окружающей среды под воздействием военной авиации [8]. Качество функционирования ВТС – техногенную опасность, в данном случае акустическую дискомфортность, приаэродромной территории будем оценивать с точки зрения двух показателей шумового загрязнения окружающей среды: y1 – «эквивалентный уровень звука» и y2 – «максимальный уровень звука».

В табл. 4 представлены исходные данные, промежуточные расчеты и результаты построения интегральной оценки акустической дискомфортности первоначального списка объектов шумового мониторинга.

Таблица 5. Показатели шума, абсолютные оценки качества окружающей среды, относительные и интегральная оценки акустической дискомфортности объектов шумового мониторинга с дополнительной информацией

Номер п/п	y 1	y 2	μ 1	M 1	Л M1	μ 2	M 2	Л M 2	Л D 1	Л D 2	D	Ранг
1	94	75	0,310	0,323	0,245	0,255	0,319	0,057	0,256	0,360	0,310	10
2	56	48	0,953	0,908	0,454	0,939	0,894	0,122	0,100	0,156	0,129	2
3	82	70	0,513	0,508	0,336	0,381	0,426	0,075	0,165	0,267	0,217	7
4	89	76	0,395	0,400	0,287	0,229	0,298	0,053	0,207	0,390	0,305	9
5	92	81	0,344	0,354	0,263	0,103	0,191	0,027	0,233	0,773	0,583	11
6	98	71	0,243	0,262	0,206	0,356	0,404	0,072	0,321	0,280	0,301	8
7	87	50	0,429	0,431	0,302	0,888	0,851	0,119	0,192	0,160	0,177	3
8	88	54	0,412	0,415	0,295	0,787	0,766	0,113	0,199	0,171	0,185	5
9	107	73	0,090	0,123	0,092	0,305	0,362	0,065	0,818	0,313	0,646	12
10	88	53	0,412	0,415	0,295	0,812	0,787	0,115	0,199	0,168	0,184	4
11	109	88	-	0,092	0,092	-	0,043	0,043	0,819	0,489	0,696	13
12	88	45	-	0,415	0,415	-	0,957	0,957	0,117	0,001	0,061	1
13	101	79	— -	0,215	0,215	— -	0,234	0,234	0,304	0,071	0,196	6

К первоначальному списку объектов шумового мониторинга были добавлены три «новых» наблюдения с номерами 11-13. Результат построения интегральной оценки акустической дискомфортности объектов шумового мониторинга с дополнительной информацией приведен в табл. 5.

Ранжировка первоначального списка объектов шумового мониторинга имеет следующий вид: 2, 7, 10, 8, 3, 6, 4, 1, 5, 9; а для списка с дополнительной информацией – 12 , 2, 7, 10, 8, 13 , 3, 6, 4, 1, 5, 9, 11 (полужирным начертанием выделены объекты, добавленные в первоначальный список). Таким образом, для элементов первоначального списка ранжировка сохранилась, т.е. «новые» объекты шумового мониторинга «добавились» в первоначальную ранжировку.

Предлагаемая интегральная квалиметрическая оценка функционирования ВТС является нелинейным (неаддитивным) критерием качества управленческих решений и отличается от аналогов тем, что:

• 1)    имеет содержательную и вероятностную интерпретации, что необходимо для формализации понятия «опасность (риск)» функционирования ВТС;

• 2)    позволяет непосредственно учитывать требования (нормативы) к качеству функционирования ВТС в виде нормативных уровней – нижних предельно допустимых значений по каждому ПК в отдельности;

• 3)    частные показатели качества функционирования ВТС могут быть измерены в различных шкалах (шкале отношений, интервальной шкале, в порядковой шкале, в виде балльных оценок);

• 4)    возможен учет неравноценности частных оценок качества функционирования ВТС на основе определения их весовых коэффициентов;

• 5)    применима в системах мониторинга управления функционированием ВТС.