Кванто-химические расчёты в кремнии

Квантовая химия –это направление химии, рассматривающее строение и свойства химических соединений, реакционную способность, кинетику и механизм химических реакций на основе квантовой механики. Благодаря быстрому развитию квантовой химии были разработаны достаточно эффективные полуэмпирические и неэмпирические варианты метода молекулярных орбиталей (МО).

На практике обычно пользуются как полуэмпирическими, так и неэмпирическими методами. Для неспециалиста название "неэмпирический" является синонимом слова "точный", но в действительности это не так. Неэмпирические методы также являются приближенными, прежде всего из-за неполноты использованного базиса. Большинство неэмпирических расчетов проводят в базисах небольшого и среднего размеров. Это вносит существенную ошибку в результаты расчета, так как такие базисные наборы не могут передать некоторые особенности распределения электронной плотности в молекулах. В результате все без исключения параметры молекул вычисляются с некоторой ошибкой. Было бы желательно (хотя на практике это сделать очень трудно из-за больших затрат машинного времени) использовать достаточно большие базисы, которые обеспечивают выход на так называемый хартри-фоковский предел, когда дальнейшее увеличение числа базисных орбиталей не влияет на полученные результаты. Но даже в этом случае мы найдем не точное решение уравнения Шредингера, а лишь его решение в приближении Хартри-Фока. Для получения точного решения уравнения Шредингера необходимо еще учесть электронную корреляцию.

Полуэмпирические расчеты в настоящее время чаще всего проводят в валентных приближениях ППДП, ЧПДП и ПДДП [1].

Известно, что эмпирические методы квантовой химии являются с вычислительной точки зрения наиболее эффективными, но они не содержат явную информацию об электронной структуре, что сильно ограничивает их применимость, например, к неизвестным структурам или структурам с различным типом химической связи.

Для того, чтобы уменьшить вычислительные затраты в данном случае, как уже отмечалось выше, предпочтительно использование полуэмпирических МСС. Существующие варианты МСС можно разделить на две группы по способу представления полной энергии системы. В методах первой группы [1,2,3,4], которые назовем стандартными МСС, полная энергии системы записывается в виде

E_{to t}= E_reР +  NЪ + E_a „                         (1)

o       rep                     a

i где 8i и Ni - энергия i-го электронного состояния и число электронов в нем, первый член в (1) соответствует энергии отталкивания (энергия отталкивания ядер (или остовов атомов) минус энергия отталкивания электронов; последняя входит дважды во второй член), а последний - энергии изолированных атомов, используемой нередко в качестве подгоночного параметра. Сравнительное исследование [5] указанных вариантов МСС для исследования дефектов в кристаллическом кремнии показали, что увеличение сложности функциональных форм не обязательно приводят к улучшению получаемых результатов. Для большинства статических и динамических свойств ни один из этих форм оказались не лучшими остальных. Более того, самосогласованный вариант стандартного МСС [4] также не приводил к улучшению результатов, например, в случае исследования кластеров кремния.

Таким образом, эти МСС скорее исчерпали свои потенциальные возможности с точки зрения возможности дальнейшего их улучшения точности и надежности для применения для неизвестных структур, в особенности для богатого множества наноструктур, лежащих между небольшими молекулами и массивными материалами. МСС, предложенный в работе [6], который назовем нестандартным МСС (НМСС), в отличие от стандартных МСС, основан на другом выражении для функционала полной энергии и использует относительно небольшое количество параметров, имеющих определенную физическую смысл и связанных с показателями экспоненты слейтеровских атомных орбиталей (АО) [7,8], которые характеризуют меру протяженности волновых функций электронов в атомах.

В настоящее время метод молекулярно-динамического (МД) моделирования [9] стал эффективным и достаточно надежным теоретическим инструментов для детального изучения динамики атомов и связанных с ней свойств многоатомных систем (твердых тел, поверхностей, дефектов, полимеров и т.д.).

Одна из первых попыток в этом направлении предпринята авторами рабоы[10].Они использовали хорошо известных метод CVD с неблоьшой модификацией, а именно PECVD. То есть обычный метод CVD с дополнительной плазменной стимуляцией. До опубликования работы[10] люминесценция на малоразмерных частицах кремния, полученных из CH 4 /H 2 в плазме или при магнетронном распылении, уже наблюдалась[11,12].С 3

другой стороны, также были описаны попытки создания нанокристаллических пленок кремния для целей фотоники. Однако в работе [10] представлены результаты первого наблюдения видимой ФЛ от нанокристаллических пленок кремния, сформированных методом PECVD. Во время нанесения пленки подложки нагревали до температуры 230⁰С. В реакторе газ CH 4 разбавляли аргоном и одновременно добавляли водород. Скорость нанесения составляла 1,5 нм/мин. Обычно удавалось создавать пленки нанокристаллического кремния толщиной 0,2-0,5 мкм на нанокристаллической кремниевой подложке. Одна из последних публикаций [13] как раз и посвящена доказательству получения лазерного эффекта на материале, представляющем собой агрегаты из ультрамалых частиц кремния. Процесс формирования таких частиц и собственно создание материала состоит в электрохимическом травлении монокристалического кремния в HF и Н ₂ О ₂ [14-15]. При этом используют катализаторы, способствующие образованию наночастиц. В водном растворе образуются коллоидальные агрегаты, затем они переносятся в акриловую кислоту,из которой частицы уже извлекаются в оболочке из акрилового полимера. Ультразвуковая обработка дает возможность разделить частицы по размерам и таким образом получить материалы, люминесцирующие на определенных длинах волн в видимом диапазоне излучения. Показано, что сфероидальные частицы размером порядка 1,0 (Si ₂₉ ), 1,67 (Si ₁₂₃ ), 2,15, 2,9 и 3,7 нм излучают в УФ-,голубом,зеленом желтом и красном диапазонах спектра для для четырех наименьших указанных частиц[16].

В данном разделе мы провели кластер с димеризованной поверхностью является наиболее выгодной структурой в рамках расчетов метода функционала локальной плотности. В данной главе мы рассмотрим расчеты кластера Si 29 , проведенные нами в рамках нетрадиционного метода сильной связи в комбинации с методом молекулярной динамики. В частности, первый параграф посвящен результатам расчетов кластера Si 29 с димеризованной и недимеризованной поверхностью. Во втором параграфе будет рассмотрено 4

влияние зарядового состояния кластеров на его конфигурацию и поверхностную реконструкцию.

На рис. показаны геометрии кластеров Si 29 , с чистой алмазоподобной геометрией (рис.а) и поверхностной реконструкцией типа димеризации (рис.б).

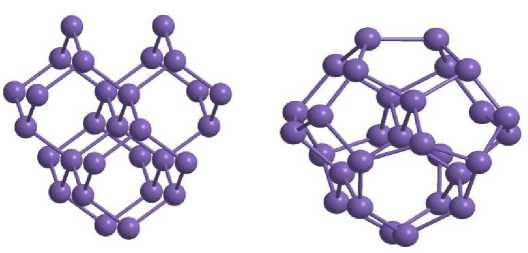
Рис.а. Рис.б.

Мы провели расчеты кластера как с оптимизацией геометрии, так и без оптимизации. Оптимизация геометрии проводилось методами молекулярной динамики и Флетчера-Пауэлла. Все расчеты являются самосогласованными, т.е. с учетом перераспределения электронной плотности между атомами. При этом, метод оптимизации Флетчера-Пауэлла производится с сохранением начально выбранной симметрии кластера, тогда как молекулярнодинамические расчеты позволяют определить релаксированную конфигурацию кластера без учета какой-либо симметрии.

Литературы: