Квантовая частица на плоскости Минковского

По мере развития нанофизики появилась возможность создания новых материалов на основе метаатомов, т. е. искусственных структур более или менее простой формы размером в несколько нанометров [1]. В частности, получены материалы, которые демонстрируют свойства металла в одном направлении и ведут себя подобно диэлектрику в ортогональном направлении. Они получили название гиперболических метаматериалов [2, 3]. Действительно, именно в пространствах с псевдоримановой метрикой имеется два типа прямых (помимо изотропных), которые не совмещаются изоморфизмами и поэтому позволяют моделировать две разные физические сущности в рамках одного пространства [4, 5].

Бурное развитие метаматериалов в последние несколько лет, заманчивые перспективы их практического применения в самых разных областях стимулируют теоретические исследования поведения частиц в пространствах с нетрадиционной метрикой. В настоящей заметке рассмотрена простейшая задача об уровнях энергии нерелятивистской квантовой частицы, у которой собственное пространство представляет собой плоскость Минковского. Для предотвращения смешивания разных типов прямых на изотропных прямых помещены потенциальные барьеры бесконечной высоты. В отличие от стандартной задачи с евклидовой плоскостью, где частица имеет только непрерывный спектр, в случае плоскости Минковского у нее дополнительно появляются дискретные уровни энергии.

1. Полярные координаты

Плоскость Минковского – двумерное пространство нулевой кривизны с псевдоевклидовой метрикой s ² = x 1 — x 2 в декартовых координатах. Декартовы и полярные координаты в областях I ( x 1 — x 2 >  0 , x i >  0) и II ( x 1 — x 2 >  0 , x i <  0) связаны формулами (см. рисунок)

( xi = ±r ch ф      ( tg r = л/x 1 — x2 > 0,

( x2 = ±r sh ф     | thф = x2/xi,

где r € [0, то), ф € R.

x1

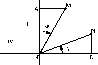
Рис. Полярные координаты {r, ф} точки M и координаты {р, х} точки N на плоскости Минковского. OM= r , ON= р .

Fig. Polar coordinate {r, ф} of point M and coordinate {р, х} of point N on Minkowski plane.

В областях III ( x 1 — x 2 <  0 , x ₂ >  0) и IV ( x 1 — x 2 <  0 , x ₂ <  0) вместо мнимого r вводим вещественный радиус р = Vx 2 — x 1, т.е. r = ip, и новый угол χ, отсчитываемый теперь от оси x ₂ и связанный с углом ф соотношением ф = х — i ^п , тогда ( x 1 = ±р sh х       ( th р = ^x 2 — x 1 >  0 ,

( x 2 = ±р ch х,      \ th х = x 1 /x 2 ,

(2) где р Е [0 , то ) , х € R .

Асимптотически при больших r убывающее на бесконечности решение уравнения (5) ведет себя как u(r) ~ enr. Поэтому можно искать его решение в виде u (r )= r 2 + iM e-nr f (r). (10)

Тогда для функции f ( r ) получаем уравнение

2. Квантово-механическое поведение частицы

Для уравнения Шредингера в области I в полярных координатах

rf ‘‘ + (2 iM + 1 — 2 nr ) f ‘ — 2 n Q + iM^ u = 0 ,

(11) частными решениями которого будут вырожденные гипергеометрические функции

F Qm + | , 2 iM + 1 , 2 nr) ,

• —   д1Г+ + ¹ д -  (Г² ) ^ф( г,ф ) = E ^ф( г,ф )

2m \ dr2   r dr r2 дф2 / с граничными условиями Ф(0, ф) = Ф(то, ф) = 0 ищем решение в виде

• *( г,ф ) = Vr)    ,          (4)

r

(2 nr ) 2 iM F Q — iM, 1 — 2 iM, 2 nA-   (12)

где функция u ( r ) удовлетворяет уравнению

Общее решение уравнения (5) дается линейной комбинацией

u ( r )= C 1 u 1 + C2u 2 = C ( u 1 — e ^{- 2} i^Y u 2 )    (13)

функций

( 2 mE  M ² + 1 \

+      +---.4 Г = 0

~ ²         r ²

u 1 = e

— ■

^nr Vr' r iM F (MM + 2 , 2 iM + 1 , 2 nr) ,

с эффективным потенциалом притяжения

u 2 = e

— ■

ηr r r

— ■

iM F (I — iM, 1 — 2 iM, 2 nr) -

_- ~² M ² + ¹ ₄

U eff ( r ) = <    ^{2 m r 2}

∞,

r >  0 , r = 0 .

Таким образом, предполагается, что на изотропных прямых находится бесконечно высокий потенциальный барьер, который препятствует уходу частицы из области I. Одномерная задача (5) с сингулярным потенциалом рассматривалась в работе [6], §35, где, правда, отмечено, что она не имеет непосредственного физического смысла. Приводимая в данной заметке интерпретация придает ей определенный физический смысл. Подробное решение этой и подобных задач с сингулярным потенциалом дано также в работах [7, 8].

При малых r волновая функция u ведет себя как [7, формула (2б)]

При малых r функция u ( r ) стремится к нулю (7), но ее производная — к бесконечности. Поэтому немного модифицируем граничное условие при r = 0 . Выпишем уравнения (5) для разных значений E

2 mE u ‘ 1 +

~ ²

‘‘   / 2 mE 2

u ^{2 +}    ~ 2

+

+

u ( r ) ~ Vr Ar iM + Br ^iM ) ~

~ Vr (riM — e 2iYr iM) ~ Vr sin(M In r + y), поскольку при малых r уравнение (5) имеет вид

u ’’ + Mr u = 0

с решениями в виде суперпозиции функций r ^{1 2 + iM} и r ^{1 2 -iM} . Здесь γ – фаза отражения от сингулярности r = 0 (0 <  y < n ) .

Дискретный спектр существует при отрицательных значениях энергии E , поэтому удобно обо-

значить

η ²

2 mE ~ ²

m ² + 4 r ²

M ² + 4 r ²

u 1 = 0 ,

u 2 = 0 .

Умножим первое уравнение на u 2 , второе – на u 1 , вычтем второе из первого и проинтегрируем от нуля до бесконечности

∞

У ( u 1 u 2 ‘ — u 2 u1 ) d r = 2 m ( E 2

Воспользовавшись равенством

∞

— E 1 ) I u 1 u 2 d r.

( u ₁ u ‘ 2 — u ₂ u ") = ( u ₁ u 2 — u ₂ u 1 )       (18)

и ортогональностью функций u ₁ и u ₂ , получаем

( u 1 u 2 — u 2 u 1 ) I ~ = 0 .           (19)

На бесконечности и сама функция и ее производная стремятся к нулю, а в точке r = 0 имеем

( u 1 u 2 — u 2 u ‘ 1 ) 1 0 ~ sin( y ( E 1 ) — Y ( E 2 )) -    (20)

Откуда следует условие квантования

Y ( E 1 ) — Y ( E 2 )= nn.          (21)

При r → ∞ вырожденная гипергеометрическая функция имеет асимптотику

F(a, b; z)

Г( c)

∼

Rez^^ Г(a)

e z z ^a-c .

Поэтому волновая функция (13) ведет себя пределе как

в

этом

u(r^enr е-i(m n) Г(1 + 2iM) u(r) e V        Г( i + iM)

2iY) r(1 - 2iM) ) Г(1 - iM) ) '

-

-

e i ( M ln n-

тогда из условия u ( то ) = 0 находим

e‘

i(2M ln n-2Y) = Г(1 + 2iM) Г(1 - iM)

'           Г(1 - 2iM)Г(1+ iM)’

откуда

Подставляя энергий

Y (E) = M ln п + C (M) .

в (21), получаем дискретный

(25) спектр

En = E0e M , n = 0, ± 1, ±2,..., E0 < 0,

(26) что совпадает с формулой (34) в [7]. При увеличении n расстояние между уровнями растет и дискретный спектр при E → -∞ становится все более редким. Для положительных энергий E >  0 спектр непрерывный.

В области III уравнение Шредингера в переменных ρ, χ записывается в виде (3) со знаком плюс в левой части. Если вновь искать решение в виде (4), то приходим к уравнению Шредингера (5) на полуоси р 6 (0 , то ) с энергией E = -E и эффективным потенциалом вида (6). По-прежнему на изотропных прямых находится бесконечно высокий потенциальный барьер, который препятствует переходу частицы из области III в какую-либо другую область плоскости Минковского. В области III дискретный спектр будет при положительных энергиях, а непрерывный – при отрицательных.

Замечание. Общий случай комплексной фазы

Y = Y 1 + iY 2 , 0 <  y 1 < п, y 2 >  0 (27) отвечает варианту “полупрозрачного” барьера (с регулируемой высотой “стенки”) на изотропных прямых. Тогда возникают интересные решения, связанные с туннелированием (или просачиванием) из области I в область III и обратно. Случай γ ₂ → ∞ отвечает полному поглощению частицы на изотропной прямой, что можно толковать как переход частицы в область III.

Авторы благодарны И.В. Костякову за полезные обсуждения.

Работа выполнена при частичной финансовой поддержке Программы фундаментальных исследований УрО РАН, проект № 18-1-1-7.