Квантовая кулоновская частица на плоскости Минковского

Прогресс в нанофизике привел к созданию новых гиперболических метаматериалов, которые демонстрируют свойства металла в одном направлении и ведут себя подобно диэлектрику в ортогональном направлении [1–3]. Это стимулируют теоретические исследования поведения частиц в пространствах с нетрадиционной метрикой. В частности, в работе [4] рассмотрена простейшая задача об уровнях энергии нерелятивистской квантовой частицы, у которой собственное пространство представляет собой плоскость Минковского. В отличие от стандартной задачи с евклидовой плоскостью, где частица имеет только непрерывный спектр, в случае плоскости Минковского у нее дополнительно появляются дискретные уровни энергии. Аналогично у кулоновской частицы имеются неустойчивые состояния, описывающие падение частицы на изотропные прямые, образующие метрический конус.

Кулоновская частица на плоскости Минковского

Плоскость Минковского – двумерное пространство нулевой кривизны с псевдоевклидовой метрикой s ² = x 1 — x 2 в декартовых координатах. Декартовы и полярные координаты в областях I ( x 2 — x 2 >  0 , x i >  0) и II ( x 1 — x 2 >  0 , x i <  0) связаны формулами (см. рисунок)

\ xi = ±r ch ф [ x2 = ±r sh ф j r = ^ x 2 — x2 > 0,

( th ф = x 2 /x 1 ,

где r G [0 , го ) , ф G R .

U eff ( r)l

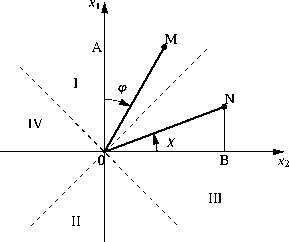
Рис.1. Полярные координаты {r, φ} точки M и координаты {ρ, χ} точки N на плоскости Минковского. OM= r , ON= ρ .

Fig.1. Polar coordinate {r, φ} of point M and coordinate {ρ, χ} of point N on Minkowski plane.

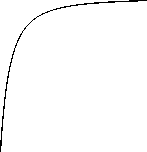
Рис.2. Эффективный потенциал кулоновской частицы на плоскости Минковского.

Fig.2. Effective potential of Coulomb particle on Minkowski plane.

В области I уравнение Шредингера с потенциалом U ( r ) = — а в полярных координатах имеет вид

При малых r волновая функция u ведет себя как

u ( r ) ~ V r sin( M ln r + Y ) ,          (8)

~ 2

2 m

(£+1 4— 4 4) •< - ^ )+

∂r ² r ∂r r ² ∂φ ²

поскольку в этом случае уравнение принимает вид

„ M ² + 1

u ’’ ( r ) +-- _r 2 ⁴ u ( r ) = 0

+ U ( r )Ф( г,ф ) = E Ф( r, ф ) .          (2)

с решениями в виде суперпозиции решений r ¹ 2 ^{+ iM} и

1 r ²

-

^iM , где γ есть фаза отражения от сингулярного

Если ввести оператор импульса L = —i~ фф , то это уравнение можно записать следующим образом

—

2 m

д ²     1 д

L ²

dr ² r dr   ~ ² r ²

^ Ф( г,ф )+

+ U ( r )Ф( г,ф ) = E Ф( r, ф ) .          (3)

конуса r = 0 . Если y комплексное число, то в обычной одномерной задаче это означает наличие поглощения в точке r = 0 [5], а в нашей задаче может соответствовать прохождению частицы через изотропные прямые в области III, IV на рис. 1.

Дискретный спектр возможен при отрицательных значениях энергии E . Удобно ввести единицу длины r ₀ = „ , ~ „ , параметр g = . ,^m“ _F и без- 2 - 2 mE              ~ - 2 mE

размерную переменную z = запишется в виде

_r ^r ₀ . Тогда уравнение (6)

Его решение, отвечающее вещественному собственному числу M эрмитового оператора углового момента

u" ( z ) +

M ² + 4

z ²

+ g

z

— 4^ u ( z ) = 0 .    (10)

L Ф( ф ) = M Ф( ф ) , M G R ,         (4)

ищем в виде

При больших z убывающее на бесконечности решение асим _z птотически ведет себя как экспонента u ( z ) ~ e ^- 2 . Поэтому можно искать решение уравнения (10) в виде

Ф( г,Ф ) = ur ^ф( Ф ) . r

u ( z ) = z 2 ^{+ iM} e - 2 f ( z ) .

Тогда для функции f ( z ) получаем уравнение

Тогда из (3) для функции u ( r ) получаем уравнение

^u ( r )+(4 mE +

M ² + 1   2 ma\ , , „

-^^{A +}     ) u ( ^r ) = ⁰ <6>

Таким образом, задача свелась к одномерному уравнению Шредингера с эффективным потенциалом

U eff ⁽ r ) =

-

~ 2 m 2 + 4

2 m  r ²

-

α

. r

zf" + (2 iM +1 — z ) f ‘ — ( g +j+ iM^f = 0 .

(12) Его базисными решениями будут вырожденные гипергеометрические функции [6]

a z    a ( a + 1) z ²

^{f i (} z ) = F ⁽ a^,c,z ) = ^{1 +} с - ⁺ с ( c +1) ^y ⁺ ..., f 2( z ) = Ф ( a, c, z ) = z ^{1 -c} F ( a — c + 1 , 2 — c,z ) ,

Она возникает в релятивистских уравнениях для кулоновского поля и разобрана, например, в работах [5,7].

где с = 1 + 2 iM , а = iM + 2 — g .

Имеем три типа решений уравнения (10) u 1 = C ie ^{- 2} Vz z iM F iM^^ + 2 — g, 2 iM + 1 , z^ ,

u 2 = C 2e ² Vz z iM F f 2 — iM - g, 1 - 2 iM, z

— e ^{- 2} i^Y

u ( z ) = C i u i + C 2 u 2 = C ( u i - e ² i^Y u 2) .   (14)

Рассмотрим первое решение. Чтобы функция u 1(z) стремилась к нулю при больших z, нужно, чтобы ряд (13) обрывался. Это возможно при a = —п, п = 0,1,2..., тогда собственные значения пт

E ( n,M ) =-------------2 ,    (15)

2 ~ ² n + iM + 2)2

а волновая функция

Ф1 ( z, ф ) = C 1e - 2 z iM F ( —n, 2 iM + 1 ,z ) e ^Мф .

При вещественных M = 0 имеем неустойчивые распадные состояния, излучающие в сингулярный центр по интерпретации работы [8]. В нашем случае это соответствует поглощению изотропным конусом или прохождению из области I в области III, IV на рис. 1. При M = 0 получаем синглетные состояния с дискретным спектром, такие же, как на евклидовой плоскости при M = 0 , что совершенно естественно, так как в этих случаях частица движется только в радиальном направлении. Однако, поскольку уравнение (2) инвариантно относительно замены r → -r , то частица переходит из области I в область II на рис. 1, в отличие от евклидовой плоскости, где она поглощается центром.

Нетрудно заметить, что первое и второе решения (14) связаны простой заменой M ↔ -M , поэтому второе решение – это просто комплексное сопряжение первого u ₂ ( z ) = u * ( z ) .

Рассмотрим последнее решение u ( z ) , представленное в виде суперпозиции первых двух (14). Теперь уже одновременно оборвать ряд у u 1( z ) и у u ₂ ( z ) не удается. Посмотрим, как ведет себя это решение при больших и малых значениях аргумента. Когда аргумент z стремится к нулю, волновая функция ведет себя как [5]

Г(1 — 2 iM ) Г (2 — iM — g )

)

Чтобы оно стремилось к нулю, нужно потребовать, как и в работе [5],

Г(1 + 2 iM) = e - 2 iY Г(1 — 2 iM)

Г (2 + iM — g)        Г (2 — iM — g)'

Условие квантования (18) примет вид

Y ( E n ) — M In r 0 ( E n ) =

= y (E 0) — M In r o( E о) + пп(22)

или           f (En) = f (E 0) + пп,(23)

где

, Г (1 — g ( E ) + iM )

f ( E ) = —M In g ( E )+arg ¹ ^(^ ,M ) ^} . (24)

При больших отрицательных значениях энергии (т.е. при малых r ) и M = 0 функция f ( E ) и —M ln g ( E ) . Тогда для уровней энергии получаем, как и в работе [5], формулу

2 πn

E n = E 0e Mr ,             (25)

совпадающую с уровнями энергии для свободной частицы [4]. Действительно, в этом случае эффективный потенциал приблизительно равен

U eff ^{( r} )

~ ² M ² + 4

2 m  r ²

т.е. определяется только орбитальными силами. В работе [9] такие решения названы ”режимом падения на горизонт событий”.

Для стремящихся к нулю отрицательных энергий (больших значений r и g ( E ) ) функция f ( E ) и —ng ( E ) и уровни энергии даются формулой

E n

u ~ Vz ( z iM — e ² i^Y z ^iM ) ~ Vz sin( M ln z + Y ) ~

mα ²

2 ~ ² ( п + g 0) ² ’

п = 0 , 1 , 2 ,...

~ Vr sin( M In r + y - M ln r 0) .     (17)

Фаза а = y - M ln r 0 зависит от энергии а = а ( E ) и можно воспользоваться условием квантования [5]

а ( E n ) — а ( E о) = пп.           (18)

Асимптотика функции u 1( z ) и u ₂ ( z ) при z ^ ∞ имеет вид [6]

u i( z ) ~ e ²

g Г(1+2 iM )

Г ( 2 + iM — g ) ’

При g 0 = 2 получаем формулу, описывающую уровни энергии кулоновской частицы на евклидовой плоскости. Таким образом, при удалении от изотропного конуса происходит сгущение уровней, точно так же, как и в обычном кулоновском потенциале при удалении от притягивающего центра. Действительно, в обоих случаях в этой области энергий ведущим является как раз кулоновский потенциал. Поскольку при больших значениях g ( E ) квантовые числа п тоже большие ( n ≫ g 0 ), то для уровней энергии в этой области приблизительно можно записать

u ₂ ( z ) ~ e ²

g Г(1 — 2 iM )

Г (2 — iM — g ) ’

mα ²

—-----— .

2 ~ ² п ²

тогда решение u ( z ) на бесконечности ведет себя как

Эффективный кулоновский потенциал [10] на евклидовой плоскости (рис. 3)

u ( r ) ~ u i( r ) — e ² i^Y u ₂ ( r ) ~

U eff ( r ) =

z

~ e ² z

—

g / Г(1+2 iM )

V ^Г (2 + iM — g )

~ ^{2 1} ₄ - M ²

2 m  r ²

-

α

, r

-

только знаком при M ² отличается от потенциала (7) на плоскости Минковского (рис. 2).

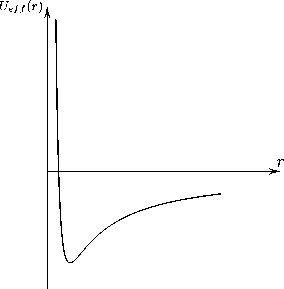
Рис.3. Эффективный потенциал кулоновской частицы на евклидовой плоскости.

Fig.3. Effective potential of Coulomb particle on Euclidean plane.

Подобный эффект изменения знака возникает в релятивистских уравнениях Дирака и Клейна-Гордона для кулоновского потенциала [9], где для частиц с зарядом Z меньше некоторого критического заряда Z < Z _кр реализуется евклидов случай, а для частиц с зарядом больше критического Z > Z _кр - случай плоскости Минковского.

Работа выполнена при частичной финансовой поддержке Программы фундаментальных исследований УрО РАН, проект № 18-1-1-7.